Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Chapter 4
Zero-Order Approximation
4.01 Separation of Zero-Order Terms from Series
We proceed to extract, from the series-expansions established in the
preceding chapter, a set of approximate equations in which the only
displacements that appear are those of order zero. Isolation of the
zero-order terms could be effected by setting
u^f*
=0 for «>0 in all of
the series-expressions, but the result would be of little practical value.
This is essentially because the zero-order thickness-stretch depends only
on the first-order thickness-displacement (i.e., Sf^ = u^, see Fig. 3.031)
so that, if u^ = 0, the plate is constrained to remain at constant
thickness during any deformation. For example, a simple tension in the
plane of
the
plate would not be accompanied by thickness-contraction. In
addition, if we consider the possibility of variation of strain with xi and
x
3
, we see that, if uSf =0 for «>0, the strains S\
l)
and S^ would
be suppressed (see Fig. 3.032). These strains are required if we are to
have zero-order thickness-stretch which varies with x\ and X3. The
difficulty does not arise to as great an extent with u^ and u^ for,
although they appear in the zero-order strains S^
0)
and Sf^, they are
101

102 Mathematical Theory of Vibrations of Elastic Platesy
not the sole contributors to those strains. Accordingly, we begin by
setting
«<">=0, M
3
(n)
=0, «>0
w<
n)
=0,
n>\
(4.011)
These assumptions reduce the kinetic energy-density (3.0514) to
K=pb(u\
0)
u[
0)
+ «<°>
«<°> +u<%™ ) +
-pb
3
u^ (4.012)
and the strain-energy-density (3.0511) to
£7
=
1
2
rh/W dw
(0)
^»
(0)
T
(0)
0U
\
+
yr(O) ^3
+ T
(0)
OU
2
+
j,(0)
dx,
dx dx,
(du™ du\
0)
i,
8x
l
dx
3
J
rbA
0)
rhjW rbjW
&!
3x,
(1)
dx,
(4.013)
We may eliminate the contribution of u\' to the vibrational energy.
without suppressing u^
itself,
by setting
««=0
(4.014)
in (4.012) and
r2
(0)
=7
.0)
=r<
(i)
=0
(4.015)
in (4.013). In so doing, we eliminate the lowest order of thickness-stretch
vibrations, just as we have already eliminated the higher order
thickness-stretch vibrations, by setting u^ =0 for n>\, and all the
thickness-shear vibrations by setting u[
n)
=
u
(
3
n)
=0 for n > 0. By
setting r
2
(0)
= T
4
(1)
= T
6
(1)
= 0 in (4.013) and wf=0 in (4.012), we
permit the free development of not only the zero-order thickness-stretch
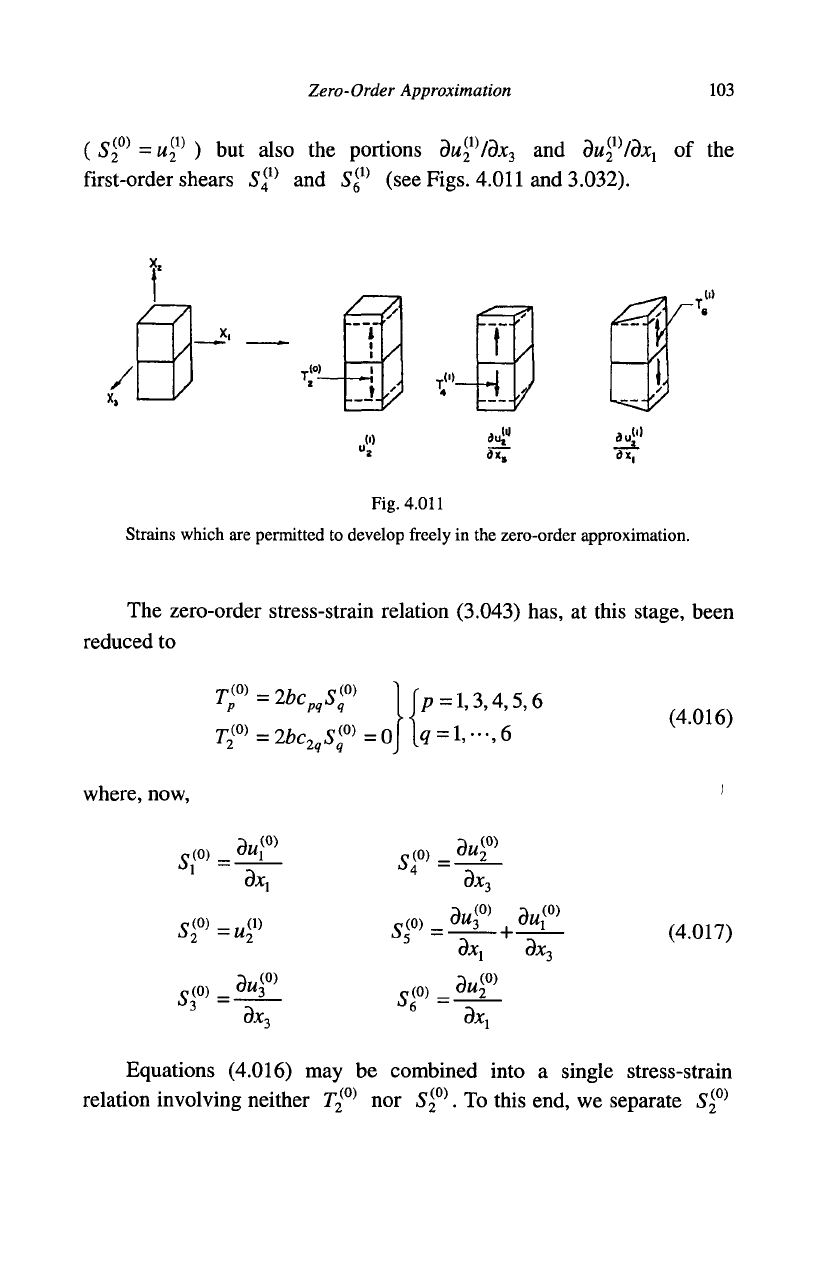
Zero-Order Approximation 103
( Sf
=
M
2
) but also the portions du^'/dx^ and du[
)
/dx
l
of the
first-order shears S^ and S^ (see Figs. 4.011 and 3.032).
/
x,
/_
to)
1
.__ —
1
'/
-J
V
y
a*.
Fig. 4.011
Strains which are permitted to develop freely in the zero-order approximation.
The zero-order stress-strain relation (3.043) has, at this stage, been
reduced to
-(0)
_ .
(0)
Tr=2bc
pg
S^> I fp = l,3,4,5,6
T™ =2bc
2q
S™ =0) U
=
l,-,6
(4.016)
where, now,
£(0) _
aU
l
dx,
1J9 — W9
^(0) _OU
3
dx^
o(0)
O4
S
5
(0)
=
c(0)
°6
_a
M
f
9JC
3
_M
0)
dx
x
_a«f
a
Ml
(0)
3^3
(4.017)
Equations (4.016) may be combined into a single stress-strain
relation involving neither r
2
(0)
nor S^
0)
. To this end, we separate S^

104 Mathematical Theory
of
Vibrations
of
Elastic Plates
(0)
2
in the first of (4.016) and solve the second equation for
S^
T^=2b(c
pq
S^-c
p2
S^)
+
2bc
p2
S
5
(0)
=
_^
5
(
0)+5
(0)
(
4
-
018
>
c
22
The expression for
S
2
0)
in the second of (4.018) is then substituted for
the
S
2
0)
outside the parentheses in the first of
(4.018),
with the result
T
p
[
0)
=2bc
pq
S
q
°\
p,q
=
l,-,6
(4.019)
where
C
PI
c
pq
C
pl
C
2q
'22
This is the stress-strain relation for the zero-order approximation.
It
may
also be written
Tj
0)
=2bc
ijkl
S<$\
i,j,k,l
=
l,2,3 (4.0110)
where
c
ykl
-c
vkl
-^^L
(4.0111)
C
2222
The stress-displacement relation is, from (4.0110) and (4.017)
TP=bc
m
iufJ
+
u^)
(4.0112)
The final expressions for the energies are, from (4.012)-(4.015),
K
=
pbitfuf
(4.0113)

Zero-Order Approximation
105
Then
-he <?(°><f<
0)
-
OC
ijkl^ij
°H
p
dS™
9
35<°>'
^<
0)
' "
(4.0114)
(4.0115)
In view of the approximations, the zero-order stress-equations of
motion reduce to
T^+Fp=2bpiif
(4.0116)
or
ox,
ax
3
•}
T
(0)
WO)
^i-
+
^
+
F
2
(0)
= 26/»<
0)
(4.0117)
OX,
OX
3
ar
(0)
wo)
—— + —-
dx
l
dx
3
+
^^
+
F
3
m
=2bpu?
It then follows, from (4.0112), that the displacement-equations of motion
are
c
ijkl
[b{uf) +«<»>)],
+
F}'
n
=2bpu™ (4.0118)
There remain stresses and equations of motion of orders higher than
zero;
but,
as
shown in the next section, they need not be taken into
account.
4.02 Uniqueness of Solutions
We consider two sets
of
displacements, strains, tractions and

106 Mathematical Theory
of
Vibrations of Elastic Plates
stresses in
a
plate and designate their respective differences by starred
symbols. Then the kinetic energy-density and strain-energy-density
of
the difference system are
K*=bpuf*uf*
(4.021)
iT=bc
m
S^sr
(4-022)
If K*
and U*
are the total kinetic energy and strain-energy
of
the
plate, calculated from
K* and U*
and reckoned over
a
time interval
t-t
0
, we have, as in (1.051),
K* + U* = K*(/
0
) + U*(t
0
) +
f'
dt
f
(K*
+
U*)dA
(4.023)
Now
K*
=
2bpiif*uf*
and
-,
_ dU
•
(0)
.
M
v
=
7
,
*
0)
*w
(0)
*
=(rr«D.i-^
(
7«r
where use has been made of the fact that, since the quantities
in
each
system satisfy
the
stress-equations
of
motion
and the
stress-strain-displacement relations,
so do
their differences. We have,
then,

Zero-Order Approximation
107
j
A
(JT
+U*)dA
=
l
A
[(T^uf^)
J
+FJ
0)t
uf
)
*]dA
Remembering that (), ,=0 when
i=2,
we have
j
A
(T^u^X
i
dA
=
§v
i
T^uTds, v
2
=0
where s is the coordinate along the edge of the plate. The integrand of the
line integral may be expressed in terms of coordinates n, s, 2 where n is
the outward normal to the edge:
y^uf^vj^u^,
h,g=n,s,2
=
T
(0)*-(0)*
ng
u
g
since v„=l, Vj=0, v
2
=0. Hence
i<"+n'=K*((„)+u*((
0
)
+
j;
djT^r *
+
14
fr*r*
<4024)
Accordingly, by the same argument as that employed in Section 1.05,
sufficient conditions for a unique solution of the equations of motion are
a. Specification of the initial displacement HJ
0)
and initial velocity
iiy
0)
throughout the plate.
b.
Specification of one member of each of the pairs
F™u?\
F
2
(0)
«f,
F
3
<
0)
H<
0)
throughout the plate.
c. Specification, at each point of the edge, of one member of each of the
nail-* T
(0)
7/
(0)
T
(0)
»v
(0)
T
(0)
r/
0)
pairs i
m
u
n
, l
m
u
s
, l
n2
u
2
.
108
Mathematical Theory of Vibrations of Elastic Plates
4.03 Stress-Strain Relations
For the triclinic crystal, the stress-strain relation in the zero-order
approximation is, from (4.019)
-(0) _
2b
c
2
^
c
12
s<
0)
+
'22 )
Cf) C
c,, --
C,c ~-
12^23
'22 J
si
0)
+
C\iC
12
c
24
'14
sf
'22 J
T
3
m
=2b
12^25
'22 J
C-tfC-
S<
0)
+
'16
^
32^-21
'31
sl
0)
+
'22 J
'22 J
c
2
^
c
32
'22
s
3
(0)
+
s\
0)
'22 J
C-nC
32^25
T^=2b
'35
f
C
V
S
5
(0)
+
'22 J
CAOC
C
3
6--
p(0)
^6
42^21
sl
0)
+
'22 J
'22 7
CA^C
42
L
23
'43
S<
0)
+
'22 J
C
44
.2 >*
'42
S<
0)
+
'22 y
C47C
42° 25
sf +
-22 y
'46
c(0)
°6
-22 y
7
5
(0)
=2Z>
CciC
52^21
-22 y
s,
(0)
+
C^C
'53
52^23
'22 J
si
0)
+
sj
0)
+
'22 J
^55-
~
2
^
'25
S^ +
-22 ^
£^?£
C
56-"
52^26 o(0)
°6
r
6
(0)
=2Z>
V "22 J
r
C S[
0)
+
'22 J
C
62
C
23
'63
V
s
3
(0)
+
'22 J
'64
sl
0)
+
-22 y
C(-,C
bl^li
5
5
(0)
'66
'22 7
~
2
^
'26
(
'22 j
:W
(4.031)

Zero-Order Approximation
109
For
the
monoclinic crystal with
the
x
r
axis
the
axis
of
two-fold
symmetry,
Cl5=Cl6
=
C25
=
C26=C35
=
C
3
6=C45=C46=0
(4.032)
Hence
T
l
(Q)
=2b
T}
0)
=2b
T}
0)
=2b
„2
~\
:<o)
sr+
-22
J
si
0)
+
C
tt
C
2\
'31
C
CA-JC
s<
0)
+
22
J
C
33~
'22
J
.2
>\
'32
C,fC
'14
42^21
S™
+
12^24
'22
J
sT
'22
J
'34
s<°>-
'22
J
C,-,C
C
43-
42*-23
'22
J
s<
0)
+
'44
'22
/
„2
\
'22
J
:(0)
:<o)
Tr=2b(c
55
S^
+
c
56
Si
0)
)
'55
u
5
'65°5
rr=2Kc
65
^
0
>
+C66
^)
56^6
,
c(0
66^6
In the isotropic case, we have,
in
addition to (4.032),
(4.033)
C
14
—
C
24
—
C
34
~~
C
56
—
"'
C
12
—
C
13
—
C
23'
C
ll
~~
C
22
—
C
33
-L
_ ^
c
44
~
C
55
—
C
66
—
~
V
c
l 1
C
12 /
(4.034)
Then

110 Mathematical Theory of Vibrations of Elastic Plates
T
(0)
r
(0)
i
2
=
2b
=
2b
y
c
u
\
y
C
12
A
2
^
c
12
C
22 J
S,
(0)
+
(
c
\1
K
J^
A
c
12
C
22 V
s,
(0)
+
c
\\
V
2 \
c
12
C
22 J
5<
0)
2) 1
c
12
C
22 )
S<
0)
-(0) _ (0)
Tr=b(c
n
-c
l2
)S'
TP=b(c
u
-c
l2
)S^
(4.035)
r
(0) _ ,
•b(c
n
-c
l2
)Si
0)
or (see Table
1.041)
r
(0)
=
^
(5
(0)
+<
)
) =
^_
[2(/l +
^(0) ^(0)-,
1
—
V
A +
ZJU
T
(0) _
V
2bE
1-v
2
(5
3
(0)
+v5
1
(0)
) = -^-[2(/l
+
//)^
0)
+^
1
(0)
]
A
+
2/i
r
(0)
T
(0)
r
(0)
1
+
v
1
+
v
6£
sf
S<
0)
sT
=
2bjuS™
= 2bjuSf
= 2bpSP
(4.036)
1
+ v
4.04 Displacement-Equations of Motion
The displacement-equations of motion may be obtained, in scalar
form, either by expanding (4.0118) or by substituting the stress-strain
relations of the preceding section in the stress-equations of motion
(4.0117) and replacing the strains by the differential coefficients of
displacements given in (4.017).
For the triclinic crystal, we have
