Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Infinite Power Series of Two-Dimensional Equations 91
where B
mn
is given by (3.029). Thus, the «* order stress depends on all
the strains of even order if
n
is even and on all the strains of odd order if
n is odd. For example
L
P -^Cpq^c, +
3
C
pq
b
q
+
5
C
pq
b
q
+
l
p -
3
C
pq*q +
5
C
pq*q +
(3.044)
7
P ~ 3
C
«\
+
5
C
w\
+
7
C
w\
+
r
(3)_26 e(D,2*_
r
C(5)
+
...
In the unabbreviated notation, (3.043) is written as
TS»=c
Vi
ZB
nm
SV> (3.045)
m
3.05 Strain-Energy and Kinetic Energy
The strain-energy-density
becomes
1
x
-
"*
x~*
m+« ri(m) rt(n)
We define a plate-strain-energy-density
cr =
\
b
_udx
2
=\c„YL
B
^^
(
3
-
051
)
2
m n

92
Mathematical Theory of Vibrations of Elastic Plates
Then, forr=l, ...,6,1=0, ..., °°,
dU
dSl
l)
2
C/,?
??
5
"
(dS[
m)
_,_, dSi
n)
•si
n)
+ -
•7 p(w)
355°
"
?
"
as,
(/)
(3.052)
Now
dS™
(i)
dS
as}-'
95^
so that (3.052) reduces to
0, r*p
0,l*m
1,
r = p, I
=
m
0, r±q
0, /*»
1,
r
=
q, I
=
n
(3.053)
dS
0)
~ 2
Crq
^-
jB
'"
Sq
"
+
^
c
P
r
'^
B
'"'
S
p
m
(3.054)
Since/? and n are dummy indices they may be changed to q and m. Then
(3.054) becomes
-^y
=
\ZKB
lm+
c
qr
B
ml
)S^ (3.055)
but
c
rq
=c
qr
and
Bi
m
=B
ml
\
hence
at/
as<
/}
-
C
rqZ
m
jB
m
lSq
m)
(3.056)
Comparing (3.056) with (3.043), we see that

Infinite Power Series of Two-Dimensional Equations 93
r<»)=_£!i_ (3.057)
P
dS
(n)
We
may also write
tf^II^JW
(3.058)
T
(n)
=
JU
(3{)59)
provided we adopt the convention (see Section 1.03)
dSf
^k =
0>
i*j (3-0510)
Finally, from (3.043) and (3.051), we have
U
=-Y
d
T<"
)
S
<
p
"
)
(3.0511)
and similarly, from (3.044) and (3.058),
U=-YJi
n)
Sf
(3.0512)
The kinetic energy-density K is treated similarly. Thus, we define a
kinetic energy-density of the plate as
K=\
b
Kdx
2
=
- J*
pitjUjdxz
(3.0513)
Replacing
Uj
by its power-series expansion (3.012) we have, as in
(3.028),
K^YLpB^uf
(3.0514)

94
Mathematical Theory of Vibrations of Elastic Plates
or
J
J 3 J J 5 J J
+
lb
3
uW+-b
5
u
l
Pu^+...
3
J }
5
}
'
3
J J
5
J J
7
J J
(3.0515)
5
'
J
7
J
'
+
-b
5
u^u^ +-6
7
*iW
)
+h
9
ufu
(
? +...
5
v ;
7
y y
9
J J
3.06 Uniqueness of Solutions
The uniqueness theorem for the three-dimensional theory (Section
1.05) is based on the expression (1.053) of the total energy in terms of
the initial energy and the work done by the external forces:
K* +U* =K*(/
0
) + lT(r
0
)+ \' dt f
t'ji'jdS
(3.061)
where t* and w* are the differences between the two surface-tractions
and the two surface-velocities associated with two systems of stress and
displacement satisfying the stress-equations of motion and the
stress-strain-displacement relations. To adapt the uniqueness theorem to
the infinite series of plate-equations, it is only necessary to specify the
surfaces over which the surface integration in (3.061) is to be performed,
replace the integrand by its series-expansion and perform the integration
with respect to the thickness-coordinate.
The plate is bounded by the faces x
2
=±6 and the cylindrical surface
(or surfaces) £" whose generators are normal to the middle plane xj=0
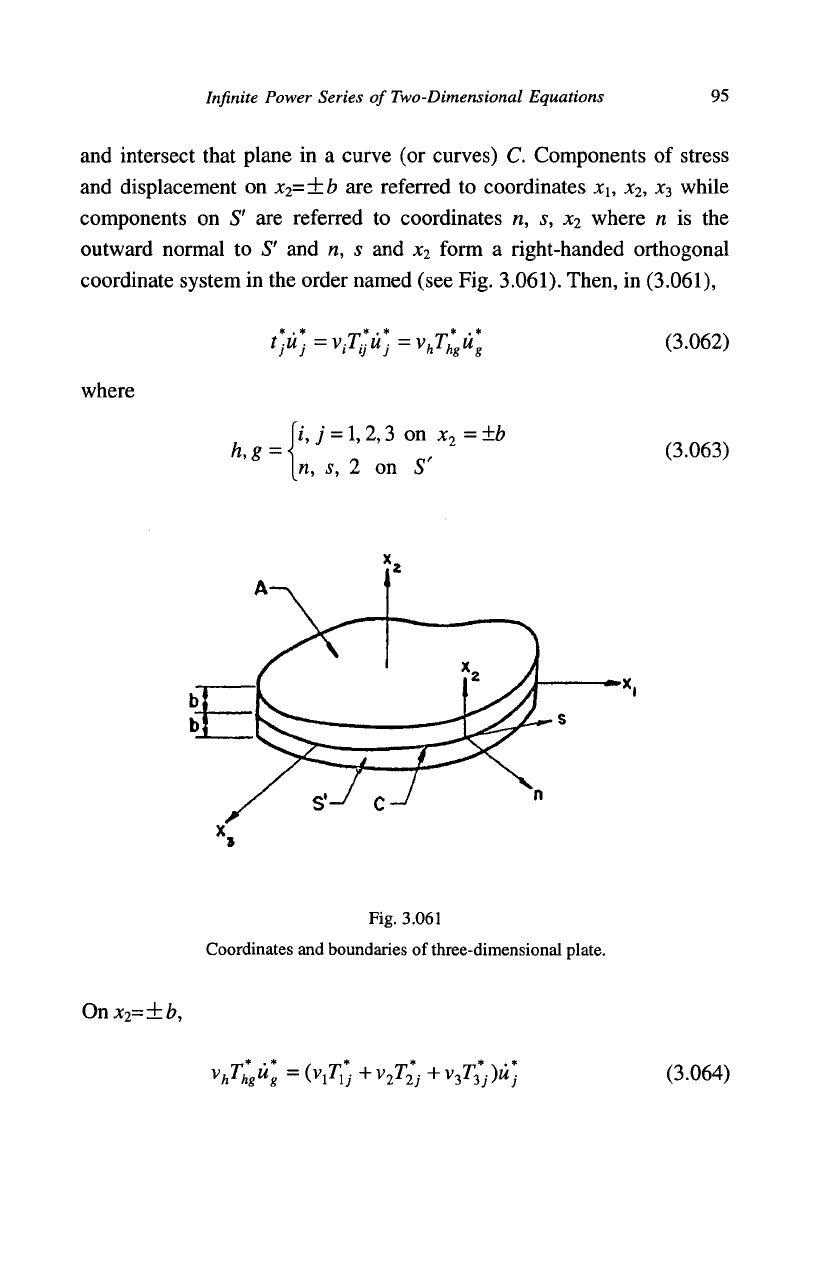
Infinite Power Series of Two-Dimensional Equations
95
and intersect that plane in a curve (or curves) C. Components of stress
and displacement on x
2
=±b are referred to coordinates
JCI,
x
2
, x
3
while
components on S' are referred to coordinates n, s, x
2
where n is the
outward normal to S' and n, s and x
2
form a right-handed orthogonal
coordinate system in the order named (see Fig. 3.061). Then, in (3.061),
where
».»
_*.» * .*
t u
•
=vT-u- =
VuTu
u
J
J i ij ] n «{"{
(3.062)
h,g =
[i,
j
=
1,2,3 on x
2
=
±b
In, s, 2 on S'
(3.063)
*-x,
Fig. 3.061
Coordinates and boundaries of three-dimensional plate.
On x
2
=+b,
V/JAX =
(
v
i
r
u
+
v
i
r
2j
+
v
3
T
v)«] (3-064)

96
Mathematical Theory of Vibrations of Elastic Plates
where
v, =0, v
9
=1, v, =0 on x-, =b
3 2
(3.065)
Vj =0, v
2
=
-1,
v
3
= 0 on x
2
=
-b
Hence
V
h
T
hgK
=
±7
2*;«*
=
iC
7
^"!*
+
T
2l»*2
+
r
23"3
) °
n X
2
=
±b
(3.066)
On the cylindrical surface
n^ng
+V
s^sg "*"
V
2^2g)"g (3.067)
where
v„=l, v
s
=0, v
2
=0 (3.068)
Hence
V
h
T
hgK
=T
ngK =
T
mK
+T
«»*
+T
n2'*2
0Ti S
'
(
3069
>
Using (3.062), (3.066) and (3.069), we have
jt]ujdS =\[T*
2j
u)t
b
dA
+\r
ng
u]dS'
(3.0610)
S A S'
where A is the area within C or between C and internal boundaries if the
plate is multiply connected.
When it* and u*
g
arereplacedby their series-expansions, (3.0610)
becomes
j
s
t'ju'dS
=j^lT*
2j
xl£
b
u*
w
dA +1j^£T*
ng
x
n
2
u
g
w
dx
2
ds (3.0611)

Infinite Power Series of Two-Dimensional Equations 97
Now, from (3.025) and (3.027)
_T;
g
x
n
2
dx
2
-T™ p,^)
fT* ir
n
t
b
— F*(
n)
Hence, the surface-integral in (3.061) becomes
n c »
n
+£E(e
)
»;
(n)
+ryuy
+
T^u
2
(n)
)ds
where a and y are orthogonal direction in the x
r
x
3
-plane.
The initial values of the kinetic and potential energies in (3.061) are
also expressible in terms of their series-expansions, through the use of
(3.051) and (3.0514). Then, sufficient conditions for a unique solution of
(3.0211), (3.045) and (3.037) are found by the same procedure as in
Section 1.05, leading, in this case, to
a. Specification, for each and every order n, of the initial
displacement «j
n)
and initial velocity u^ throughout the plate.
b.
Specification, for each and every order n and at each point on the
edge of the plate, of any one of the eight combinations formed by
choosing one member of each of the three products
T^u
(
n
n)
,
T^u^,
T(«)„(n)
l
n2
U
2
.
c. Specification at each point in the interior of the plate, for each
and every order n, of any one of the eight combinations formed by
choosing one member of each of the three products F„ '

98
Mathematical Theory of Vibrations of Elastic Plates
Fi
n)
ui
n)
.
These components are illustrated in Fig. 3.062. The conditions for
uniqueness are, of course, subject to the same limitations and extensions
as those in Section 1.05.
in) tn)
F
2
,u
2
in) m)
T
nn,
u
n
Fig.
3.062
Components of face-traction, face-displacement, edge-traction
and edge-displacement of two-dimensional plate.
3.07 Plane Tensors
It may be observed that u\
n
\ F
t
(n)
, TJ
n)
and s,y are
c-(n)
components of plane tensors; i.e., the tensors are invariant with respect to
rotation about the normal to the *
r
x
3
-plane. If the axes x\, x
2
, x
3
are
rotated about x
2
to x[, x
2
, x\ according to the scheme of direction
cosines

Infinite Power Series of Two-Dimensional Equations
99
/
x
l
x
2
x
3
x
l
'n
0
'31
x
2
0
1
0
*3
In
0
'33
the usual transformation formulas apply. Thus, if primed symbols refer
to
rotated axes and r, s,t,u=l,2,3:
y'(»)
—
7
/ T(")
rj
l
ri sj ij
T(")
_
7
I J'(")
ij
ri sj rs
C'(»)
—
/ / c(")
°»
_
'ri'sj^ij
e(«)
_
7
7 o'(")
17
l
ri sj rs
y'(")
_/ 7 y(«) _
7
7 „ c(«) _
7
7 „ 7 / c'(«)
"•re ~
l
ri
l
sj
l
ij
~
l
ri
l
sj
c
ijkl°kl
~
'ri'sj
c
ijkl
l
tk
l
ul
,3
tu
or
where
'(")
_ ' c"(«)
f'(") ' a
rafti V/
'$/
'/£ ^ul
C
ijkt

