Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


First-Order
Approximation
121
dT
(0)
dT
m
i—
+
^J-
+
F
(<»=2bpul
0)
S—
+
^2-
+
F?
)
=2bpu?
)
(5.0117)
dx
i
dx
3
ar(O)
a
r
(0)
^-
+
-^^
+
F
2
(0)
=2feX
0)
—-—
+ —-
dx
x
&
3
^«
+
OTf
_
(0)
+/?
0)
=
|
6
,
fi0
)
ox,
3x
3
3
^
+
^_
r
(0)
+F
(.)
=
^3
A
,-O)
oxj
ox
3
3
ox,
ox
3
3
Finally, from (5.0116) and (5.0112) the displacement equations of
motion are
C
,
W
[K«1
U
/
+<l+W+<?X'%
+
F;
U
'
=
2^
'ijkt
C„„[6
3
(K?J+«#)],
(5.0118)
(i)
-3fc
2
,«(
W
i°) +
«<»>
+
S
2l
u? +S
2k
uj
l)
)
+
3FV =2b>
Pl
u«
5.02 Adjustment of Upper Modes
The six equations of motion (5.0118) on the six displacements
(u\
0)
,
uj*) yield six modes of vibration of an infinite plate, each mode
with
its
own relation between frequency and wave-length. As the
wave-length approaches infinity, three of the frequencies approach zero
and three do not. The frequencies for the limiting case £=0 are readily
found from (5.0118) by setting

122
Mathematical Theory of Vibrations of Elastic Plates
F
(0) _ zr(l) _ Q
j j
uf=Afe
ia
>>\
uf=A?e"»,
r = l,2,3
5 = 1,2,3
(5.021)
where Aj and Ay are constants. Then (5.0118) reduce to
4
o
y
2)
=o
^
2Jkl
(S
2l
Ai
l)
+
5
2k
4
)
)
=
2
Pl
b
2
a>
2
s
A?
Hence, when Af * 0, Af * 0,
(5.022)
0)
r
= 0,
r = 1,2,3
V3
f^7
b \P\
where the c
s
are the roots of
5 = 1,2,3
(5.023)
-66
'26 '46
'26
'46
'22
'24
'24 '44
= 0
(5.024)
The three non-zero frequencies should be those of the three
fundamental modes of simple thickness-vibration, that is, they should be
given by (2.051) with «=1. However, it may be seen that the frequencies
are in error by a factor Wl2. The reasons for the discrepancy, and its
remedy, can be found from a study of the limiting frequencies and
mode-shapes obtained from the solution of the three-dimensional
equations. It is sufficient to examine the case of isotropic, plane strain
(Section 2.11).
In the case of flexural vibrations of an isotropic plate, in a state of
plane strain, the relation between frequency and wave-length of the

First-Order Approximation
123
fundamental mode is illustrated, for example, by the lowest dashed curve
in Fig. 2.113(a). As the wave-length increases, the frequency approaches
zero.
At the same time the displacement normal to the plate (w
2
)
approaches the form uf^ + x^u^ and the displacement parallel to the
plate («i) approaches the form x
2
u^. Similarly, for the fundamental
extensional mode, as tHb—0, u
2
~*
XjU®
and u\-~ wf'. The relation
between frequency and wave-length of the fundamental extensional
mode is illustrated by the lowest full curve in Fig. 2.113(a). Thus, for
both flexural and extensional fundamental modes, the exact solution, for
long wave-lengths, is described by just those displacements that appear
in the first-order approximation. Consequently, we may expect the
first-order approximation to be very good for long waves of the lower
modes (see Section 5.7).
Turning, now, to the second flexural and extensional modes, the
relations between frequency and wave-length, in the exact solution, are
given by the next higher dashed and full curves in Fig. 2.113(a). As £&-*•
0 these modes approach the fundamental simple thickness-shear and
thickness-stretch modes. In this case, as gb—O,
(5.025)
. . TtX
w,
—>
A, sin-
2b
The corresponding displacements in the first-order approximation are
w^ and u-f* which represent displacements linear in x
2
and lead to
limiting thickness-frequencies

124 Mathematical Theory
of
Vibrations
of
Elastic Plates
(5.026)
The error,
a
factor
Wl2, is
seen
to be due to the
incorrect variation
of
displacement through
the
thickness.
If
an
expansion
in a
series
of
trigonometric functions, instead
of
powers,
had
been employed,
we
could have obtained correct frequencies
for
the
simple thickness-modes
but the
frequencies
of the
fundamental
flexural
and
extensional modes would have been
in
error.
We can,
however, make adjustments which will correct
the
limiting frequencies
of
the
upper modes without affecting
the
fundamental flexural
and
extensional frequencies
at
long wave-lengths.
We proceed
to
trace
the
influence
of the
displacements
on the
simple thickness-frequencies.
The
latter
are
determined
by the
kinetic
energy
and
strain-energy densities.
In the
kinetic energy only
the
first-order terms
—b
3
p
l
uf
)
uf
)
contribute
to the
simple thickness-modes
and,
in the
strain energy, only
the
zero-order strain-components
Sy*
contribute.
In the
expression (5.023)
for the
simple thickness-frequencies,
the kinetic energy terms
are
represented
by the
first-order density
p\ and
the strain-energy terms
are
represented
by the
elastic constants
c
s
which,
in turn, depend only
on
c
pq
,p, q=2,
4, 6 as
shown
in
(5.024).
Thus,
we can
correct the limiting frequencies
of
the
upper modes
by
replacing
p
u
in the
kinetic energy-density
by
/J/K
2
where K
=
n/s\2 , or
by replacing
the Sfj , in the
strain-energy,
by
KS^
1
.
Neither
of
these
alterations affects
the
fundamental flexural
and
extensional modes
at

First-Order Approximation
125
long wave-lengths inasmuch
as the
altered terms contribute negligible
amounts
to the
total energy-densities
of the
lower modes when
the
wave-length
is
long.
In
this
way, we may
adjust
the
higher modes
without appreciable influence
on the
lower modes
in the
range
of
wave-lengths
to
which
the
equations
are
restricted
in any
event.
To effect
the
adjustment
of
the strain-energy,
we
have
to
replace
the
strain-energy-density (5.0113)
by
U=bK
a
K
Pc
m
sf^
+
±b%
kl
SJPsj» (5.027)
where
a-
cos
2
{ijnll)
P
=
cos
2
(kljc/2)
(5.028)
K =
ni4n
The powers
a and /?
serve
to
distribute
the
factor
K to the
thickness-strains
sf)
only
and to
multiply those strains
by
K
if the stain
appears
to the
first power
and by
K
2
if the
strain appears
to the
second
power.
In
the
abbreviated notation, (5.027) becomes
U=b
K
°K"c„sV>sV>
+
l
-b'c
pq
Sf
S
V (5.029)
where
a
-
cos
1
{pnIT)
j3
= cos
2
(q7c/2)
(5.0210)
*r
=
;r/Vl2
Then
the
stresses
are
given
by

126 Mathematical Theory
of
Vibrations
of
Elastic Plates
or
T
(0)__dU__
a
p
(
o)
iJ
~
3s<
0)
~
vu^ki
T
m __du__2.
,3-
MI)
(
0)
_ 917 _ „ « (0)
p
~as
(0)
~
w
*
r
(D _
dU
=
2
h
l
F
cO)
The stress-displacement relations become
y
iy
-OK K C
ijkl
[U
k
, +U,
k
+0
2l
U
k
+0
2k
U
l
)
r
0)_I/,3
F
/•„(•)
...OK
(5.0211)
(5.0212)
(5.0213)
and the stress-equations of motion remain unchanged.
To effect the alternative adjustment (on
the
kinetic energy)
it
is
only
necessary
to set
A=4
=
1
¥
(5-0214)
K
n
in the equations
of
Section 5.01.
It
is
apparent that the correction
on
the
kinetic energy
is
the
simpler
one
to
apply. Furthermore,
it
has been pointed
out
(Benscoter, 1955) that
this correction has
the
advantage
of
disappearing
in
the case
of
equations
of equilibrium
and
also leaves
the
elastic constants available
for
separate
adjustments appropriate
to
static problems. Accordingly,
we
shall adopt
(5.0214)
in
the
sequel (except
for
the
intermediate approximation given
in Section 6.04).
We
note that subsequent study revealed that this
was
a
poor choice. See Q. Appl. Math., vol. XIX (1961), p. 51.

First-Order Approximation 127
5.03 Uniqueness of Solutions
The establishment of sufficient conditions for unique solutions of
the equations of motion follows the pattern established in Section 4.02.
We consider two sets of displacements, strains, tractions and stresses in a
plate and designate their respective differences by starred symbols. Then
the kinetic energy-density and the strain-energy-density of
the
difference
system are
3
(5.031)
If K* and U* are the total kinetic energy and strain-energy of the
plate, calculated from K* and U* and reckoned over a time interval
t-to,
we have
K* + U*=K*(y
0
)
+
U*(y
0
)+ fdt\(T +U*)dA (5.032)
Now
T
= IpbiifufT
+-p
x
b'ufuf
(5.033)
and
fj*
=
du
c(or ,
du
c(D»
asj
0)
*
iJ
dsjp*
iJ
where the last step is a consequence of
the
symmetry of 7^
0)
* and T^*.
Noting that

128 Mathematical Theory of Vibrations of Elastic Plates
r
(0)*r •(D*_
r
(0)*-(1)*
l
ij °2i
u
j
~'2j
u
j
we have
which is converted, through the use of the equations of motion (5.0116)
to
fr
=
ff^uf*
+
T^uf*), + FJ
0),
«<°>* + FfTuf
0
(5.034)
-2pbiif
i
'uf
)
'--p
l
b
3
u^uf
Hence, from (5.033) and (5.034),
f (F+U*)dA=[ [(T^u
(
r +TV*u?*)
i
+FJ
0)
*u?
)
*+FJ
l)
*u?*]dA
JA
JA ' ' ' ' ' ' ' ' '
Then, noting that ( ),,=0 when
i=2,
we have
Icrfufr +T^uf),dA
=
§
Vi
(T^u^
+
T**u?*)ds, v
2
=0
where s is the coordinate along the edge of the plate. The integrand of the
line integral may be expressed in terms of coordinates n, s, 2 where n is
the outward-drawn normal to the edge:
Vi
a^u^
+
T^u^)
=
v
h
(^u^
+
T^u^), h,
g
=
n,s,2
_
r
(0)*-(0)*
,
T
(l)*-(1)*
1
ng
u
g
Ti
»g
u
g
since v„=l,
v
s
=0,
v
2
=0. Hence
K*
+U*
=
K*(r
0
)+U*(>
0
)
+
f '4(C*«r
+
C"D^
0
(5.035)
+ \'dt\
{F^'uf*
+
Ffuf*)dA

First-Order Approximation 129
Accordingly,
by the
same argument
as
that employed
in
Section
1.05, sufficient conditions
for
a
unique solution
of the
equations
of
motion are (see Fig. 3.062)
a. Specification
of
the initial displacements
uj
0)
, u^f and
initial
velocities
uf\
wj
1}
throughout the plate.
b.
Specification
of one
member
of
each
of the
pairs
F^u^,
F™u?\
F
3
(0
M°\
F^u®,
F®u<t\ F
3
m
u® throughout the plate.
c. Specification,
at
each point of
the
edge, of
one
member of each of
,.(0)
T
(0) (0)
r
(i)„(D
r
(i),,(i)
T(1),,(']
4
s
>
1
n2
u
2
'
1
nn"n »
1
ns"s >
1
n2
u
2
thenairs
T(°),,(°) T«>),,(0)
r
(0) (0)
r
(l)„(D
r
(l),,(l)
T(I)„(D
me pairs v„„
M„
,
i
nj
w^
,
i„
2
u
2
,
i„„
H„
,
i„
s
u
s
,
i„
2
u
2
5.04 Stress-Strain Relations
The scalar expression
of
the stress-strain relation
is
obtained
by
expanding (5.0110) and the first of (5.018).
For the triclinic crystal, we have
T™
=
2b[c
n
S™
+
c
l2
S™
+
c
a
S«»
+Cl4
5f +rf+rf]
T
2
=
2b[c
2l
S
l
+c
22
S
2
+
c
23
S
3
+
c
24
S
4
+c
25
S
5
+c
26
S
6
]
r<°>
=2^3,^
+
C
32^
0)
^33^
0)
+C
M
S<>»
+
C
35
5f
+C36
5<°>]
7-W = 2%
4l
5f
>
+
c
42
Sf>
+
c
43
5f
+
c
44
5f
+
c
45
^
+
c
46
^°>]
r
5
=2o[c
51
5'
1
+05252
+c
53
5
,
3
+c
54
o
4
+05505
+c
56
S
6
]
7f> = 26[c
61
of
>
+ <rf> +
c
63
if
>
+
c
64
Sf
+
c
65
if
>
+
crf]
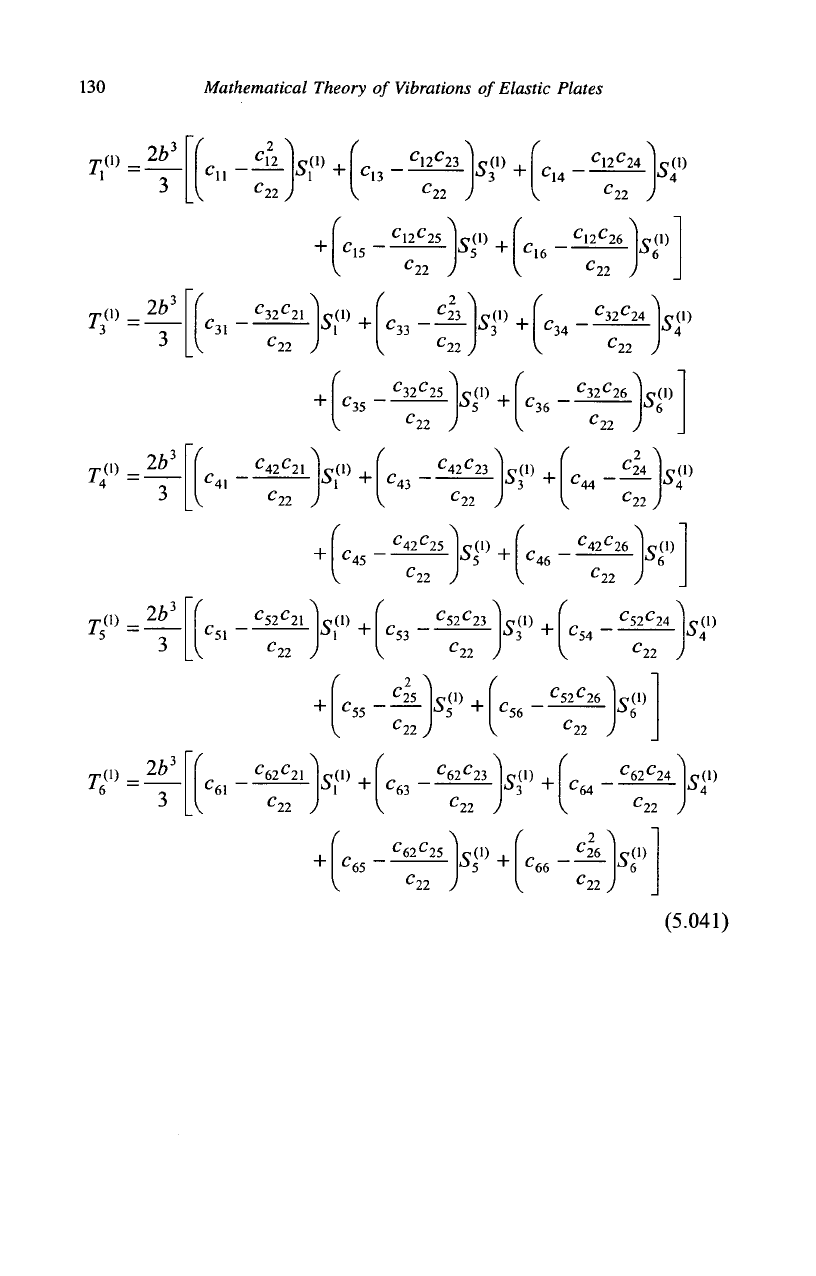
Mathematical Theory
of
Vibrations
of
Elastic Plates
2b
3
,2
\
'12
'22
^
+
+
Ct-jC
12*-23
s™
'22
J
C17C
12^24
s
4
'
(1)
C19C
12^25
$°
+
-22
y
C|
9
c
'22
7
12
t
-26
'16
•c(D
°6
-22
y
2b
3
'31
A
^
:(•)
Si
1
'
+
-22
y
+
c^c
'23
:
22y
\S™
+
C~>-fC
C34
32^24
s\
(1)
-22
y
32^25
sf
+
2b
3
'41
v
"22 y
'(1)
C-i-iC
32^26
'36 ^6
-22
y
s,
u;
+
-22
y
C
43~-
V
5
3
(1)
+
-22
y
-44
+
CA*)C
42
L
25
5«
+
2Z>
3
C^TC
52^21
v
"-22 y
,2
A
'24
-22
y
?(')
'46
cd)
°6
-22
y
s,
(1)
+
-22
y
C
52
C
23
'53
5<
,}
+
c„c 52^24
'54
s\
(1)
+
,2
A
-25
'55
26
3
Cf-fC
62^21
-22
y
v
L
22 y
Sf-H
C
62
C
23
'56
v
^22 y
c(l)
°6
-22
y
s
3
(1)
+
-22
y
^64-"
:<»
-22
y
+
'65
5^
+
-22
y
,2
A
'26
c(D
^6
-22
y
(5.041)
