Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


First-Order Approximation
131
For
the
monoclinic crystal with
the
xi-axis
the
axis
of
two-fold
symmetry,
Cl5= Cl6=
C
2
5= C
2
6=
C
35
= C
36
= C
4
5= C
4
6~0
(5.042)
Hence
rr=2b[
Cn
sr+c
n
sp
+
c
l3
s^
+CI
A
O)
]
T
2
=2o[c
21
5'
1
+c
22
S
2
+
c
23
S
3
+c
24
o
4
]
T^
=2b[c
3l
Sr
+
c
32
S^
+
c
33
S^
+
c
34
Si
0)
]
7f =2Z,[c
41
^
0)
+
c
42
5f
+C4
3^
(0)
+c
M
S?>]
T
5
^=2b[c
55
Sr
)
+
c
56
Si°
)
]
TW=2b[c
65
S™
+
c
6
X
)
]
T
m
•M
1
i
•'4
T
(i)
T
m
2b>
3
26
3
3
2b
3
3
2£
3
3
2b
3
„2
\
'12
'22
J
s[» +
Cs\")Cs
12^23
S? +
c„
-•
32
1
'21
sl
l)
+
'22
y
'33
'41
£^2Lk
(I)
+|
C
.
c
22
y
43
k^>
+C56
S«]
[c
65
S?
+
c^S,
(i)
66^6
'22
J
c
23
c
22
y
C^C
C,i
-"
12^24
'14
^
(1)
'22
y
s
3
(1)
+
^34"-
32
t
'24
^
(1)
42^23
'22
J
s<? +
'44
-22
y
4^
'22
•S«
(5.043)

132 Mathematical Theory of Vibrations of Elastic Plates
In the isotropic case we have, in addition to (5.042),
Then
'14
—
C
24
—
C
34
—
C
56
—
"
-44
—
C
55
-
C
66
_
r. (
C
l
1
C
12 )
(5.044)
7i
(0)
=2b[c
n
Sl
0)
+ c
12
(S<°> +
S
3
(0)
)]
=
2Z>[(,l
+ 2//)S<
0)
+/l(S<
0)
+
1
S
3
(0)
)]
7
2
(0)
=
2b[c
x
,
5f + c
12
(S
3
(0)
+ S
<°>)]
=
2b[{X +
2<u)S?
)
+
A(S
(
3
0)
+
5,
(0)
)]
r
3
(0)
=26[
Cll
S<
0)
+ c
I2
(S
1
(0)
+^
0)
)]
= 26[a + 2//)5<
0)
+ A(S<
0)
+ S<
0)
)]
r
4
(0
>=K
C
„-c
12
)sr
)
=2^
0)
T™=b(c
u
-c
u
)S™
=2bMSJ?>
Tr=b(c
n
-c
l2
)S^=2
bM
S^
T
m
=
T
m _
26
3
3
2b'
2
A
S,
(
(i)
C
12
-11
J
„2
A
-12
-ii;
-12
S,
(1)
,2
>\
-12
-li
y
,2 *N
'12
-11 J
-(1)
S"
2b
3
E
3(1-v
2
)
2b
2
E
3(1-v
2
)
O^+vSf)
rf^^.-c,)^^
3
/^
0
_2
3
T^=^bHcn-c
a
)S^=±b
3
MS^
(5.045)
First-Order Approximation
133
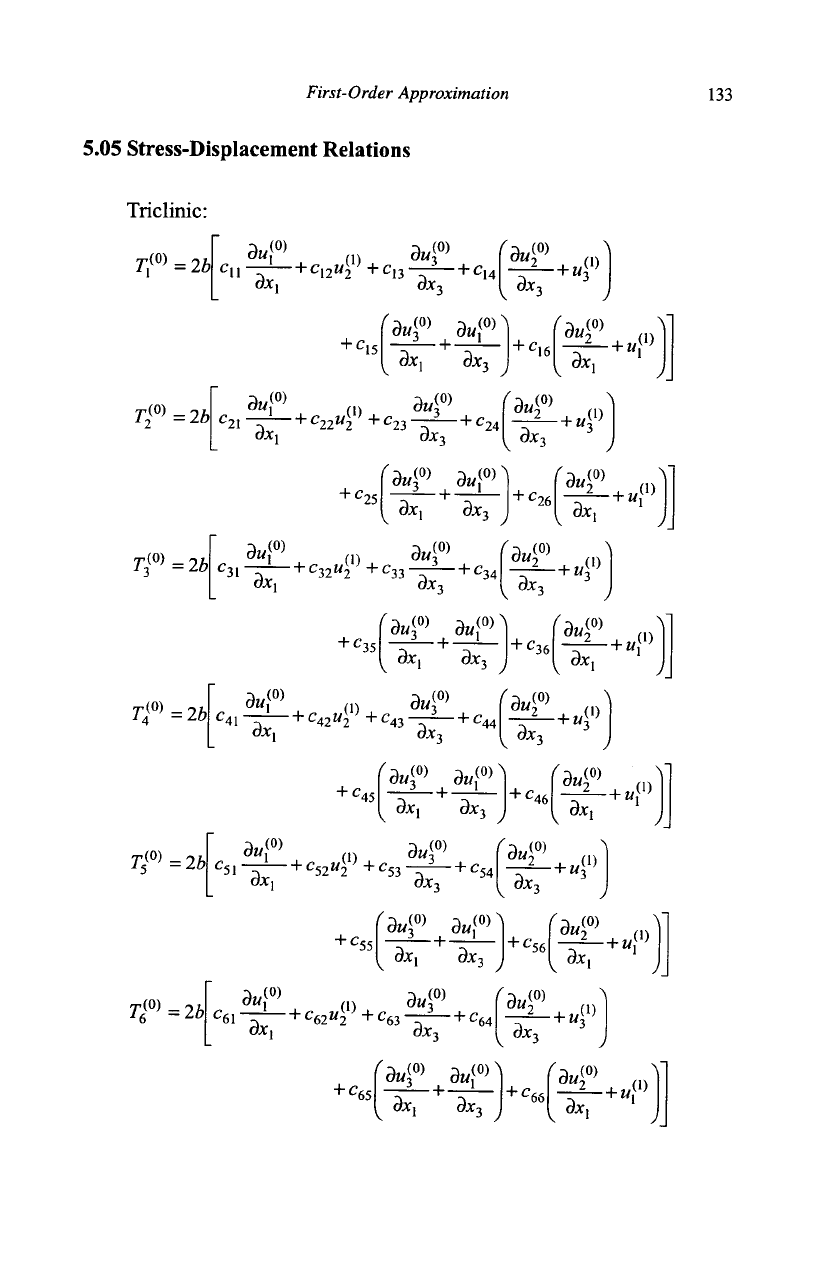
5.05 Stress-Displacement Relations
Triclinic:
3«f
- + C
14
Tf
0)
=2b
c
u^
+
c
l2
u
2
+ c,
3
——
OJC] d;c
3
I
a*, 3*
3
'*2.
+
I<
0>'
a*
3
"
3
A (
l
+
C
16
3„
+M
1
3*!
TP=2b
C
2V
ar,
+C22
"
2
+C23
1^
+C24
\-dxV
+Ui
+ c
25
T^=2b
dx
x
dx
3
j
M
0)
(,) 3«f
c
31
——
+
c
32
u
2
>+c
33
—±-
+
c
34
ox,
djc
3
3«f du\») (du^
m
^
+w
o>
9A:,
+ c
35
3
W
<
0)
3
M
,«M (du^
(1)
3x, 3x
3
r
4
(0)
=2Z>
3«<°>
(1)
a„(°)
fa
M
(")
'
o^! dx
3
[ dx
3
"2 +„('
dx,
+ c
45
TO) 1(,
3M
1
<0)
, (1)
9M
3
(
ax, 3x
3
r
dui
0)
du\
0)
—J— + —!_
. ax
l
dx
3
j
+ c
46
'*£U^
-l-M,
dx,
/J
—+C54
+ c
55
,(0)
r
6
(0)
=26
J
+——
ax
l
dx
3
M
0)
(.)
3»<°>
3x,
-+«$'
,d)
+ c
56
(
*P^
V
3x,
+ c
65
[3»f
(
3»<'
3xj 3x
3
V
)
+ M
3
dx
3
! +
C
6
6
^»(°)
...^
3JC,
-
+ u\
,(')

134 Mathematical Theory
of
Vibrations
of
Elastic Plates
-(') _
2b'
c„
—
c,-,c
„2
^
'12
a
Ml
(1
>
dx
x
+
22
J
Va.,0)
3M
(1)
nL
.
2i
,au
3
C,-)C
'13
'15
'
12
L
25
'22
J
3M,"
du.
+
0)^
V
dx,
dx-,
'22
Clfi
—
dx->
+
1
C
14
"
CITC
12^24
'22
J
du
(1)
dx-,
'12°26
'16
di/?>
'22
)
dx,
J
1 —
2b>
CiiC
(
+
c
35
V
r
(l) -
2fc3
4
" 3
'45
c
31
—
Cv)C
32
t
"21
3M
(i)
r
«-22
7
Va.,m
ate,
'33
'
,2
>
'23
'22
du
i
l)
J c
32
c
2A
]du^
+
1
c
34
32
t
-25
'22
J
du™
du\
QA
dx,
dx-, ,
V
'
3
J
+
c
36
—
3x?
'32
c
26
°"2
'22
3.x:,
'22
dx,
CA->C
'41
C
i?
C
42^21
c
22
;
Va.,0)
3M
(') /
3x,
c
43
—
'42<-23
42^25
'22
J
3«f
3M.
(1)
du
(1)
v
a
*i
3JC
3
y
-22
y
c^c
3x,
,2
^
'24
-44
ai/^
dx,
-46
'
42^26
'22
J
3M?>
3XI
7
5
-
2ft
J
c„c
c
51
—
52
t
-21
-22
y
3«,
(1)
dx,
c
^^V"^
,
C
22
J 3*3
Cc,C
'54
'
52
c
24
'22
J
du
(1)
dx-,
I
Y 3M
0
3M
,(D
'55
'25
'22
3
+
<,n,
3x,
3x,
c
56
—
'52*-26
'22
J
^du
2
»
dx,
T
m
=
lb'
c^c
62
L
21
:
22
J
du
(1)
dx,
CfoC
'63
62° 23
'22
J
du
(1)
dx-,
C(oC
'64
62^24
'22
J
du
(1)
3x,
Cf.->C
c
65
—
62° 25
'22
7
du?
3M.
(1)
—i_
+ —!_
dx,
dx-, ,
c
66
—
,2
^
'26
'22
3M
2
I}
3x,
(5.051)
First-Order Approximation
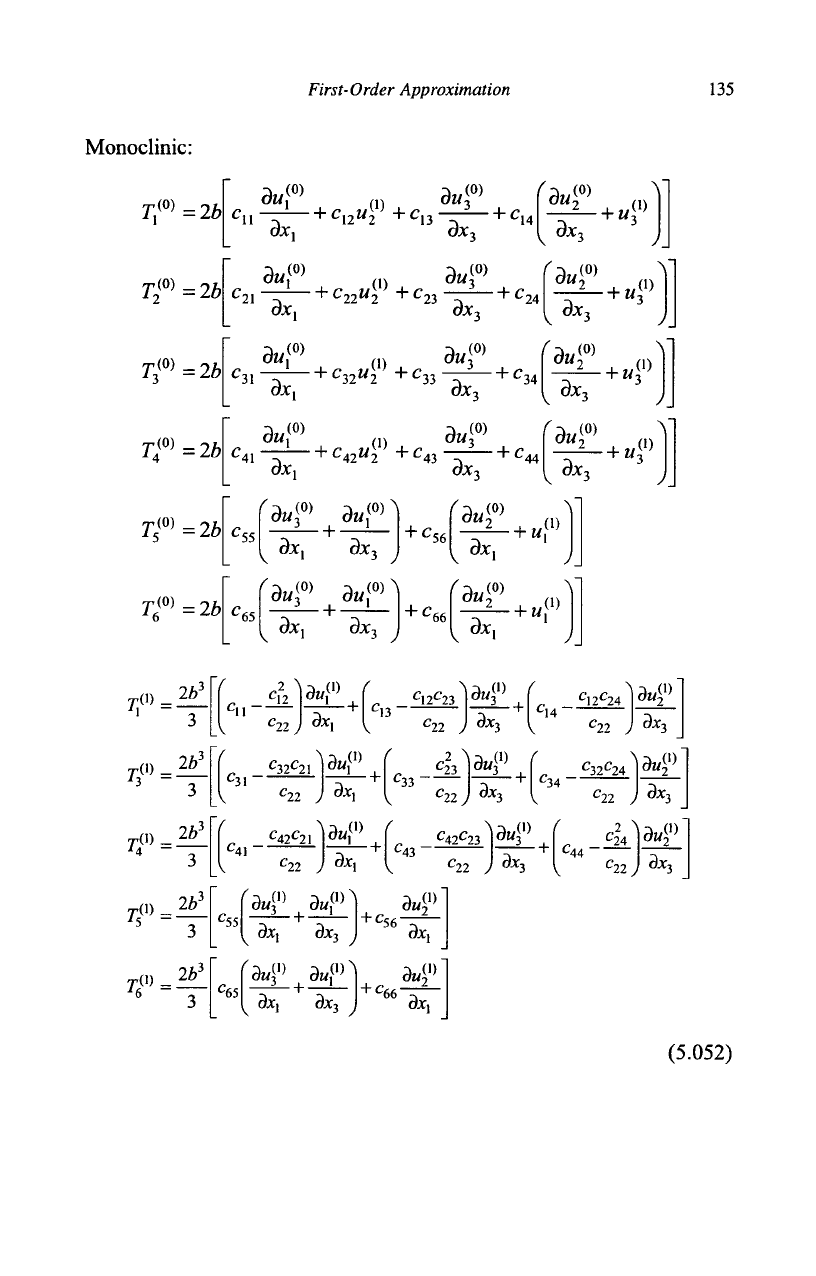
Monoclinic:
T
l
(0)
=2b
r
2
(0)
=26|
T
3
{0)
=2b\
T™=2b
T
5
m
=2b\
<0)
_
'21
du\
0)
3x,
dx,
+
C
12
M
2
+
c
13
+
C
22
W
2
+ C
2
3
dx
{
+ CTQUJ
(1)
'33
3wf
9x
3
3x
3
9i/l
0)
3x
7
+
c
14
3x,
+
W
(1)
+ C
24
3x,
•
+ u
(1)
f
;>..«»
+ c
34
du
+
C
42
M
2
+ C
43
— +
C
dx,
-
+
W
(1)
8x
44
+ C
56
'66
V
5
*i
fdu
m
du
V
3
*3
V
+
14
(1)
•
+
M
V
3
*1
2
+
M
,
(1)
r
(l)
_
jf
=
7-0) _
2A
J
2fc
J
26
J
£W>
f
L
22
3xi
c
12
c
23
3a?'
f
—*—+
L
32
c
21
L
22
J
ai/W
3x,
c
47
c
7
,
)3w,
„(')
L-22
J 3x,
L
33"
L
43~
^22 J
C
2
^
c
23
c
22;
3x,
——+
c
12
c
24
C
22
J
3x,
c,-,o
L
34"
32
L
24
L
22 ;
dx
3
dx-,
c
42
c
23
d»<'>
L
22 >/ ^3
C44
c
22
J 9x
3
7-0).
2b
3
(du^
+
Btf_)
K
3x,
X
3
7
+ C,
56"
a««
3XJ
7?)
=
2£
j
u
65
3n|'>
|
3K,
(1)
.
3xj 3x
3
1
+ C,
66"
3
M
<'>
dx,
(5
136 Mathematical Theory of Vibrations of Elastic Plates
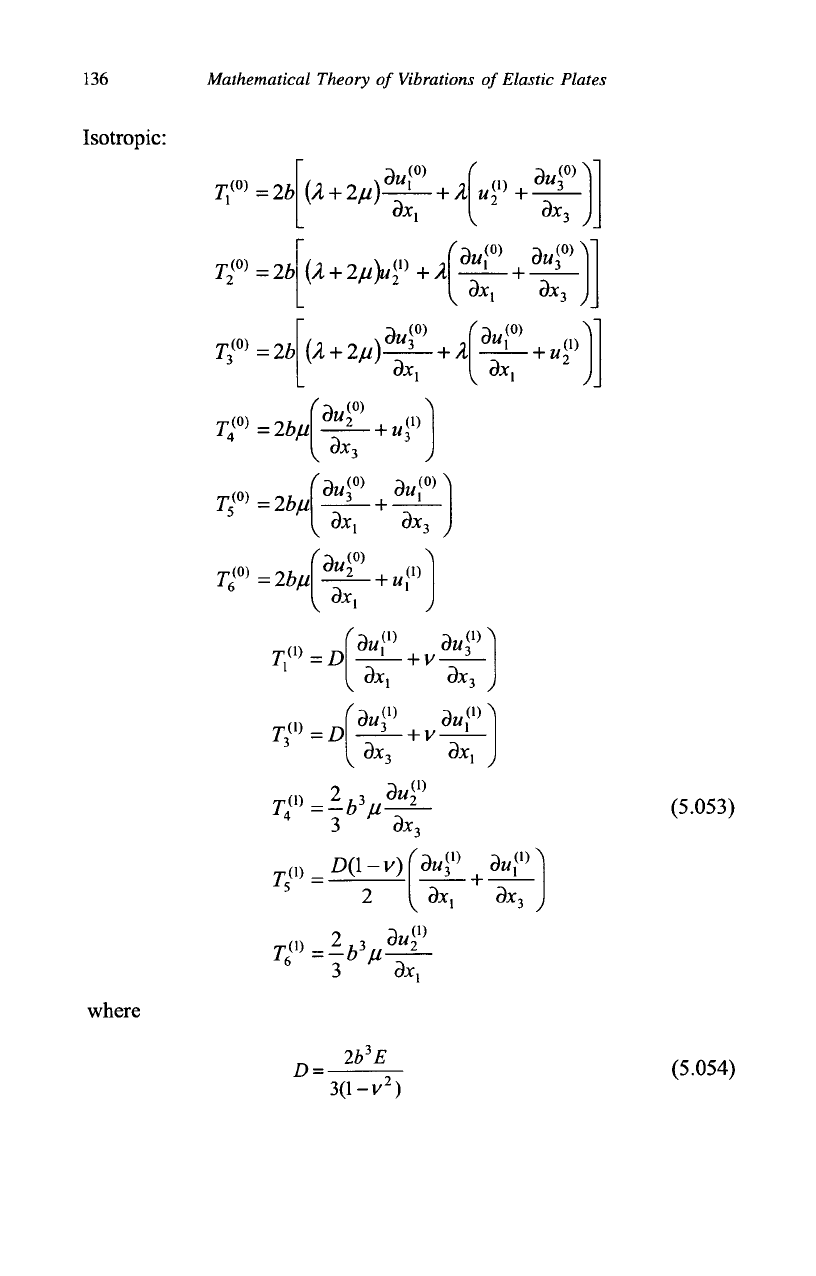
Isotropic:
-(0) _
T
l
w
=2b
7f
}
=2Z>|
T^=2b\
(A
+ 2//)^- + A|
dx,
{A +
2{i)u
(
2
)
+A
(.).^°M
«r +
dx
- + -
a«
3 ;
(0) V
3JC,
a
M
(0)
dx,
d
"'
+I/
C)
-|-M
2
T}
0)
=2b[l
(du
(0)
a*,
+
M
(1)
^
r
5
(0)
=26//
v
fa
M
(0)
r
(0) _
v
dx
i
3 +
dul
2b/i
du
l
3 y
V
3x
i
•
+ W
(1)
T^=D\
f^.m
du"
du'
+ v-
v
3x
3x
3 ;
r
3
(1)
=D!
^a^
a
M
,
(1)
^
3x,
3JC,
2,3 a^
0
^-j*'"*.
r
(l) _
i
5
_
D(l-v)
3
a«
j"
a»
0)^
v
3x
i
dx
3 ;
2,3 a^
1
'
r
6
(1)
=T*>
a*,
(5
where
£>
=
-
2b
3
E
3(1-v
2
)
(5

First-Order Approximation
137
5.06 Displacement-Equations of Motion
The displacement-equations of motion are obtained by substituting
the stress-displacement relation (Section 5.05) in the stress-equations of
motion (5.0117). The equations which follow are for plates of uniform
thickness.
For the triclinic crystal, we find
dx,
+c
dx,
+
C,-,wi
+C
a»f
(du
(0)
'12"2 "
rt
-13 ->
+c
14
dx
3
dx
2
+M
f
+ c
15
du\
U)
du
3
+- '
dx, dx-,
\ '
3
J
16
V
dx
J
dx-,
3 (0)
dx,
+
C
52
W
2
1)+C
53
du^_
dx-,
+ c 54
0X3
V
y
+ c
55
3»<
0)
a
M|
(<
M
—— +—-
dx, dx-,
V
'
3
7
+ c 56
^
+
„»
\
3x
/
A0)
+
^-
=
p*r
dx,
+ c,
'61
dul
0)
dx,
(1) ^
+
C
62
W2
+c
63~
+ c
9x
64
f^ (0)
V
3x
66
f^ (0) ~\
ax,
V
dx,
3
Ml
(0)
3bci
+
CA-,UX +C
(i)
+ c,
65
2b
•+-
J
dx, dx-,
V
'
i
J
3
M
<
0)
+ c
d
f3
M
<
0)
-42"2
"
rc
43
"T
r<
-44
dbt
3
3x
2
+ «<'>
+ c
45
3«<
0)
3
Wl
(0)
•+
3tC] 3x
3
+
c
46
MU.«>
3x
3x,
3x,
+
C
52
M
2
+c
53—
+
c
dx-,
54
J V J
+ c
^
+M
f
V
dx
'55
y
3«<
0)
3
M
<
0)
—*—+—-
dx, dx-,
\ '
3
y
+ c
56
*£
+
.»
3x
3x,
'31 '
dul
0)
dx,
+
C
3
2«2
I)+C
33
3«f
dx?
+ c
34
ar,
3
V
+ c
35
3«<
0)
du™
— • •+• '
dx, dx-,
v '
3
y
+
C
36
*£«?>
V
3x
y
F,
(0)
26
y
:/*f>
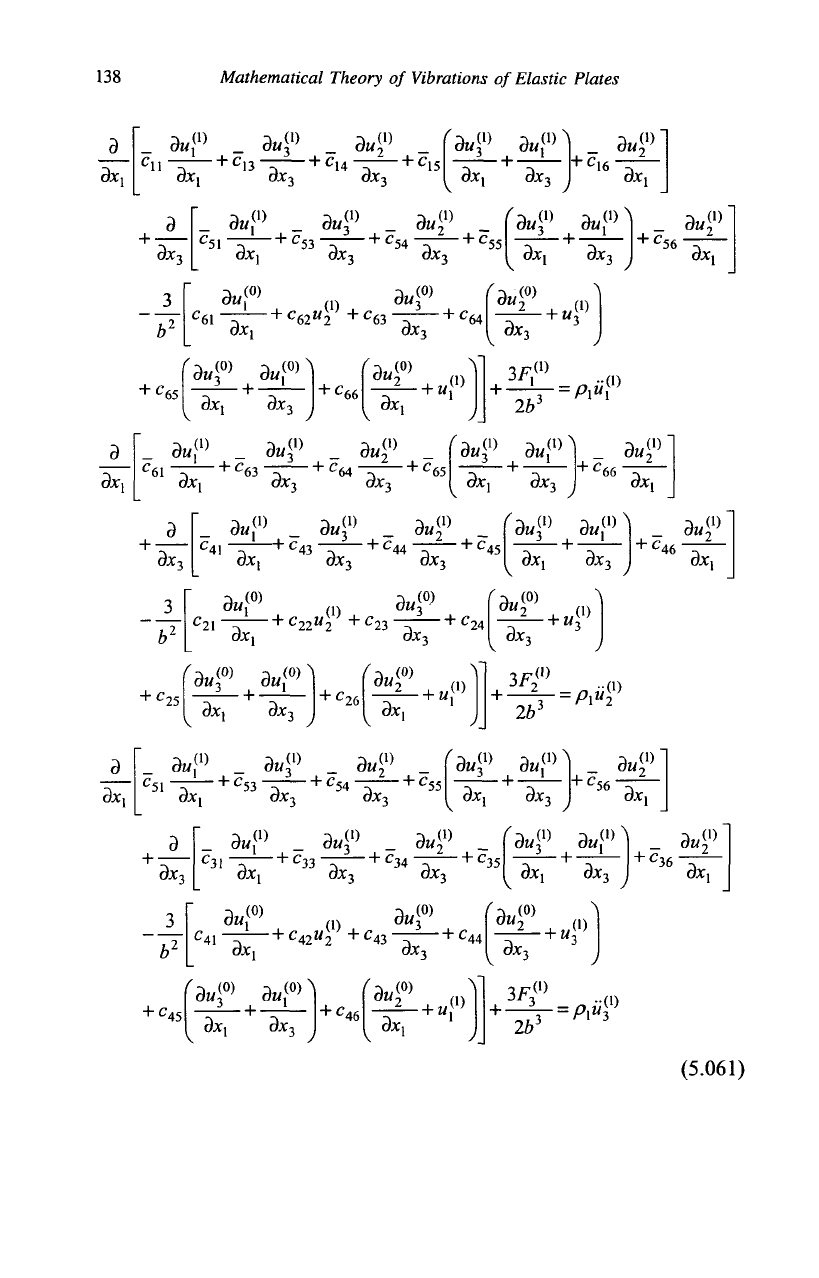
138
Mathematical Theory
of
Vibrations
of
Elastic
Plates
du{
(1)
dx, dx,
•
+ c
13
du?_
dx?
+ c
du? _
14'
dx,
• + c
15
du? du?
dx, dx-,
\ '
J
y
+ c
du?
16 '
dx,
dx,
du? - ^? - 3«f - 1^"
3".
(,)
3JC,
-+c
53 '
3x,
-
+ c. 54'
3x,
-
+
c
55
3JC[
3JC
3
+
c
56'
du?_
dx,
-61
3«,
(0)
(!)
+ c
62
u
2
+
c
63
dx
{
duf_
dx-,
+
c,
fa..(°>
+ c,
65
3w, du,
i
+ '
W\
v
^i dx
3
,
+
c,
66
dx
64
'*£-•.,»
V
3x,
M
y
r(D
•l^--"*"
3x,
du? _ du? _ du?
Cfi,
— + C.r, — + C
M
— + C,
'61
3xi
-63
3x,
-64
3;c,
65
du? du?^
+
dx
x
3x
3
,
+ c,
du?
dx,
dx,
du? _ du? _ du?
c
41
—
I-
c
43
— + c
44
—
I-
c
45
fn..O)
3A:
3XI
3;c,
3w, 3M,
O^
dx, dx,
v '
3
y
+
c
46'
a«2_
3x,
-21
dtf_
dx,
+ C
22
M
2
+C
23
3
M
f>
3JC
3
+
c
+
c
25
f3«f 3«<°>
3x, dx,
+
c
26
(^ (0)
24
V
dx,
3 (0)
-t-M
3
dx,
•
i
^2 -(I)
dx,
du? _ du? _ du?
Csi^—+ c„
—
+
c<
4
—
+ c
55
dx, ax
~
54
a
3
^3
du?
3«
(1)A
<3
_
+
„„,
3x, dx,
v '
3
y
+
c
^
56'
dx,
3x
3
C31
du?_
dx,
+
c
33
du?
dx,
+
c
34
3_^
dx,
+
c
35
j
- + -—-
dx
x
dx
3
,
+ c
3
6
du?
dx,
M
0)
(.)
£41 ~ ^"^42^2
~*~
^43
-41
dx
3wf_
dx,
(hu™
+
c.
44
2
+
U?
+
c.
45
3«<
0)
3
M
,
(0
>1
. 3xj 3x
3
(du™
+
c.
46
3x
2
+M
,
(1
>
dx
""-pun
(5.061)
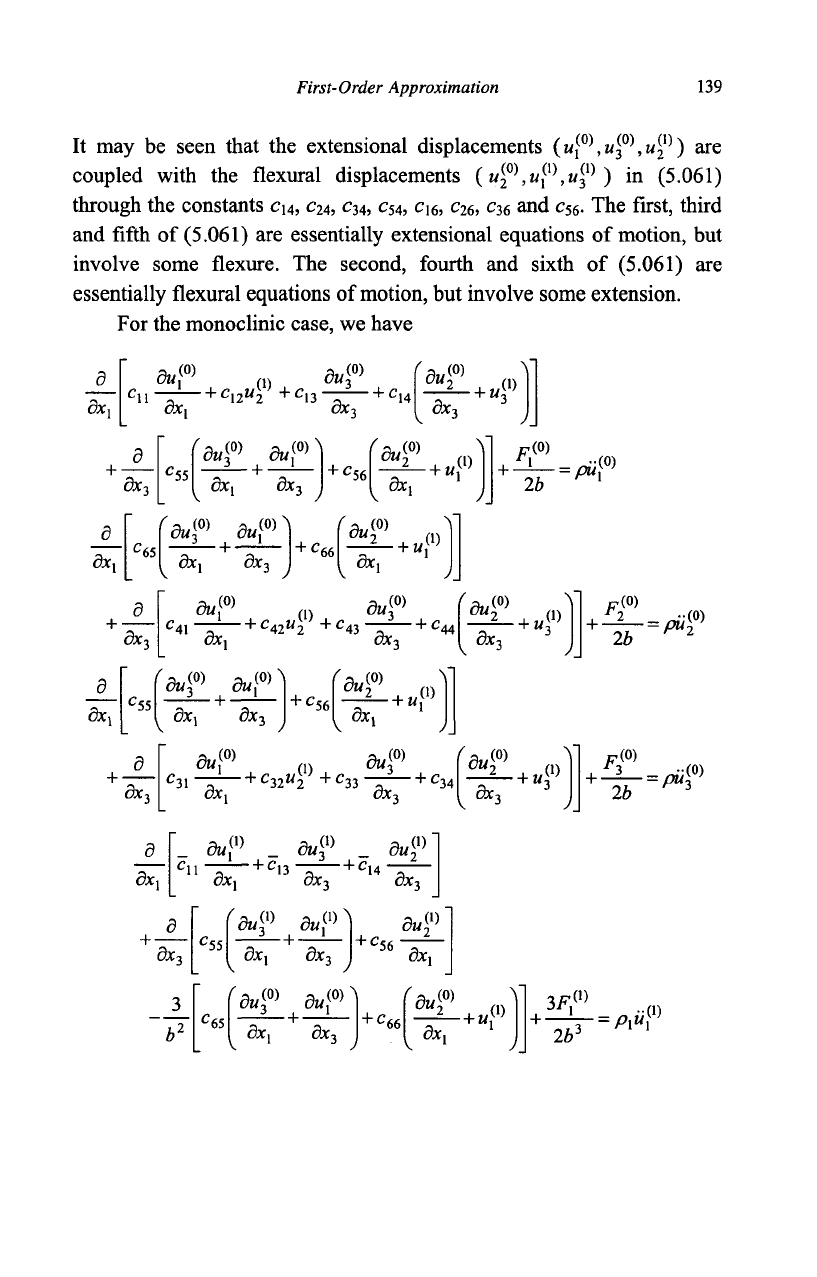
First-Order Approximation
139
It may be seen that the extensional displacements {u\°\uf\u^) are
coupled with the flexural displacements (u™,u?,u? ) in (5.061)
through the constants cu, c
2
4, c
34
, c
54
, c
i6
, c
lb
, c
36
and c
56
. The first, third
and fifth of (5.061) are essentially extensional equations of motion, but
involve some flexure. The second, fourth and sixth of (5.061) are
essentially flexural equations of motion, but involve some extension.
For the monoclinic case, we have
dx,
du
dx-,
dx
'55
(0)
' +C,
2
«2
1)+C
13
du™
du™ du.
3x
3
(0)\
f
+
c
14
dx-,
+
14
0)
dx
l
d
dx
x
-65
(du™ du,
—— + —-
dx
(0)\
+ c
56
du
V
dx
(0)
2
+u®
r(0)
26
:
PU\
(0)
dx, dx-,
(du™
+
c,
66
dx
*-
+
««
dx?
du
(0)
'41 '
3x,
+ C
d
,MT +C
-42"2
43"
du™
dx-,
+ c,
_d_
dx,
'55
dx-,
du
(o) ^
V
&, u*
3 j
dx-,
+
c
56
*^
+
.»
dx
'31
+ C
3
2«2
)+C
33'
du™
dx-,
+ c
du
(0)
dx-,
•
+ u
0)
2b
-puT
'*2U.!>'
V
ck,
26
:
P«3
(0)
d
dx,
du
(i)
5«
(i)
dx,
• + c
13
dx-,
• +
c
14
fix,
ck?
'55
'65
'du? du^
+
dx
]
'du™
V
dx-,
+
c
du?
56
/
^_
+
dul
dx
x
dx
3
+ c, 66
dx,
du™
dXy
+ u
(1)
3F
(1)
Dr
\ --(ft
-53--*".°
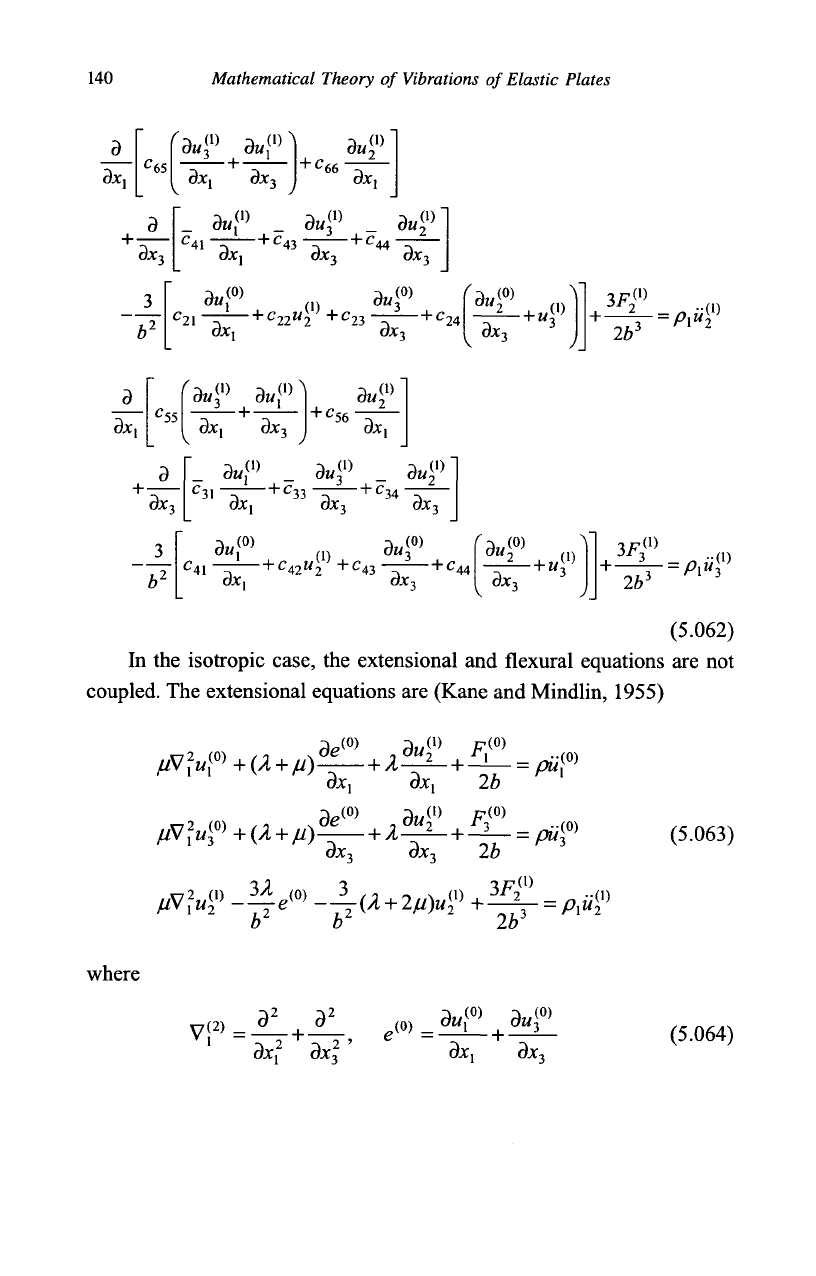
140 Mathematical Theory of Vibrations of Elastic Plates
d
dx
x
c
65
-r-+^r— +c
6
6^r-
,(')'
dx, dx
dx,
dxj
'_
3«,
(1)
_ 3»f _ duf
c
41 ~^
l
"
c
43 "^
l
"
c
44 "^
dx,
dJC
3
dx:
3
(0)
3«,
(0)
(„ K
]
C
2
\ — +C
2
2
U
2
+c
23 ~X
OX
x
0JC3
-+c
24
V
^3
3
3F
(D
2 -(n
_d_
dx
l
^55
dx,
(duf du
m
+
A
\
du\
dx
l
dxi
du?
du
2
l)
+
C
56^
dx,
du?
i—+ r„
3tt5'>'
c
31 "T '"^ ~^
hC
34 ~^~
dx, dx
3
dx
,(»)
a
M
<°>
(1)
a.™
C41
+C
42
U
2
+C43 —
dx, dx
3
•
+c
44
dx
3
/_
3F
(1)
J
3 -(I
,•;(»
CO
In the isotropic case, the extensional and flexural equations
mpled. The extensional equations are (Kane and Mindlin, 1955)
(5.062)
are not
VT2 (0) ,i
x
de
(0)
, du
(
2
ax
x
ox,
de
m
,du
(
2
x)
F,
(0
> ...
+
X——+
—!— = pu[
:(0)
1
,(•) C-(O)
1
r
* _ _ --(0)
^
(0)
dlA
l)
9x
3
9x
3
//Vf
M
<')-M
e
(0) 3
(/l +
2//)M
«
I)
+
3^
b b 2b
(5.063)
,3 M"2
where
vp=il+.
a2
9x, 9x
3
g(0)=
a«r
+
a
M
r
9x, 9x,
(5.064)
