Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Intermediate Approximations
161
In an isotropic plate, extension and flexure are not coupled in the
differential equations. The extensional equations reduce to the zero-order
approximation (see Chapter 4) and the flexural equations are those of
Chapter 5.
6.03 Thickness-Shear and Thickness-Flexure
Equations governing thickness-shear and flexural vibrations alone
may be obtained by setting
,(0)
-u?>=uV
-0
(6.031)
in the equations of the first-order approximation. Identical equations are
obtained by setting
Cl4= C
U
= C
3
4=
C
54
=
C]6= C
2
6=
C
i6
=
C
56
=0
(6.032)
in either the equations of the first-order approximation or the equations
of Section 6.02.
In the case of the triclinic plate we obtain the stress-displacement
relations
(6.033)

162 Mathematical Theory of Vibrations of Elastic Plates
and the displacement-equations of motion
dx,
'64
du^_
+ u
(1)
+
c,
66
*£V
V
dx
\
J
+
-
dx,
-44
<9w,
V
8x
3
•
+ u
(1)
+ c
46
V
5
*i
/
_5_
cbc,
_
5
Ml
(1)
- 5wJ
!)
-
dx,
•
+ c
13
dx,
•
+ c,
5^
SM^I
V
5
*i
1L.
+ ^L
Sx
+
-
dx
3
_3_
6
2
_
a»,
(1)
_
a»<'>
_
C
51 -
+ C
53 -
+ C
55
8x
l
dx,
3 v
V
dx
i
dx
3 y
'64
(
^T
,
..(.)'
V
9X
3
• + Ui
+
c,
66
dx,
+ u
(i)
+
3F
0)
2b
3
M
(,)
3x,
_ du\
l)
_ aw*
1
) _
- —— +
c„——
+
c
'51
cbc,
b
2
'53
3x,
55
dx
t
dx
3
du™
_ du^ _ fa/^ a/}"
-44
cbc,
'duj
0)
•
+ c
33
dx,
+ c
35
+
i etc, dx
3
j
•
+ u
(i)
+ c.
46
a«<
0)
v
dx
\
\
•
+ u
(1)
1P(I)
•"l
"(11
(6.034)
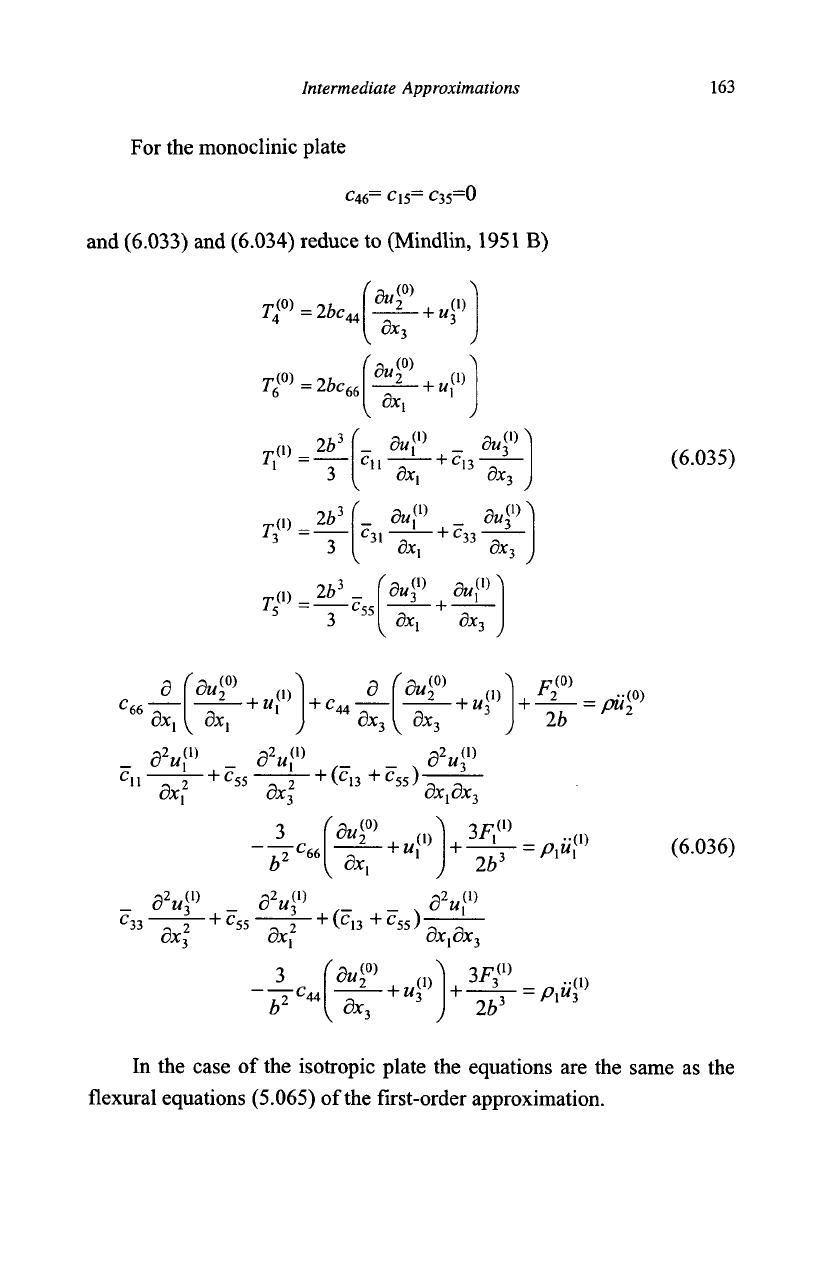
Intermediate Approximations
163
For the monoclinic plate
C
4
6=
Ci5=
C
35
=0
and (6.033) and (6.034) reduce
to
(Mindlin, 1951
B)
•*«>)
,(0)
:26c.
(du
m
44
dx
2
-
+
u^
rr=2bc,
fdu
m
66
dx
2
+M
,
(1)
r,
(1)
=
26
3
r,
(l)
=
26
_
Siil
0
_
en—— +
c,
OXi
9M
0)^
dx->
-0)
3
26
3
_
a*.
(1)
_ St/f
-31"
&•
'33 '
dx-,
-55
+
V
fix
5x
(6.035)
-66
fix,
^fi7y
(0)
^2_
+
M
<>)
V
_
e
2
w
,
(1)
fix,
+ c
44
fix,
a,<°>
fix,
+
W
(1)
+
F
2
(0)
26
= /*?>
•2„(D
fix,
2
•
+ C
a^u
55
dx
2
•
+ (c
13
+c
55
)
_
x
e
z
w
2„<1>
fix^Xj
A
2
'
66
^
0)
V
dx
l
\
-
+
u
(1)
;-(!)
1F
V
y
26
J
_ 3V'>
-33
fix
+ c«
3
—
+
(c
u
+c
55
)
-55
fix
5x,5x
3
fix,
+
W
(1)
+
3F
3
(1)
26
3
:
A
«»
(6.036)
In
the
case
of
the isotropic plate
the
equations
are the
same
as the
flexural equations (5.065) of the first-order approximation.

164 Mathematical Theory of Vibrations of Elastic Plates
An alternative procedure, which leads to equations of the same form,
but with slightly different constants, is to set
T
m
=T
{0)
=T
(0)
=Q
(6.037)
in (6.025) and eliminate the strains
5'
1
(0)
, 5
3
(0)
,
S
5
(0)
. The only changes
in (6.034) are the replacement of the c
pq
by y
pq
and the replacement of
C44,
c
66
and c
46
by
'66 °44
_ 2 ' _ 2 ' _ 2
S
M
S
66
S
46 * 44*66 ^46 * 44*66 ^46
respectively.
(6.038)
6.04 Classical Theory of Low-Frequency Vibrations of Thin Plates
The equations of the classical theory of thin plates are obtained by
suppressing the thickness-shear strains in the equations of Section 6.02.
The result is a set of coupled flexural and extensional equations of
motion (Cauchy, 1829, p. 9). When the coupling coefficients are dropped,
the equations separate into a single flexural equation and a pair of
extensional equations (Cauchy, 1829, p. 13). In the isotropic case, the
extensional equations are those of Poisson (1829, p. 499) and the flexural
equation is that of Germain (1821) except for the term accounting for
rotatory inertia, which was given later (and then dropped) by Poisson
(1829,
p. 533).
To effect the reduction of the equations of the preceding section to
those of the classical theory, we begin by setting
Sf> =Q, ^
0)
=0 (6.041)
so that

Intermediate Approximations
165
,0)
dx,
,0)
du
(0)
dx-,
(6.042)
It is to be noted that the components of rotation
duT
dx,
—
u
(1)
dufl
dx-,
-u
(i)
(6.043)
do not vanish as a result of (6.042).
In view of (6.042), the first-order stress-displacement relations
(6.025) become
r,
(1)
=-
„(i)
T®=-
.2*1
3
.2*!
3
26
3
Xn
e
2
M
f
ftl
d
2
uf
dx
2
a
2
«f
+ rn
5
2
M
f
e
2
«f
+ 2y
x5
-
2
-
+ ^33-
a
2
»(
0)
dx
• +
2y
35
dx
i
dx
J
+
T53
d
2
uf
S
2
wf
+ 2^55
dx
2
dxidx
3
(6.044)
The zero-order components of stress r
6
(0)
and T^ may be
expressed in terms of the displacement uf^ by means of (6.044) and
the fourth and sixth of the stress-equations of motion. Thus, from
(5.0117)
-(0) _ pd)
6
-
M
ST*
(1)
dT,
(i)
dx
x
dx-,
(m m
ar,
(1)
ar,
(1)
r
4
(°)=F
3
(1)
+—^—+•
3
2*_
3
2b
3
,-;(!)
fix
fix-
•A«I
A"f
(6.045)
The last terms in (6.045) account for rotatory inertia. They will be
omitted (following Poisson) inasmuch as they provide a negligible
contribution at the low frequencies to which the ensuing equations are

166 Mathematical Theory of Vibrations of Elastic Plates
restricted. Then, inserting (6.044) in (6.045), we have
2
6
-r
l
2b
3
3
Yn
dx>
+3ri5
dx
2
dx
+(rn+2r55)
dxd
X
>
+r35
J
L/Aj t/Ai CM-3 C/Aj l/Ai CM-3
2b'
3
ox
l
ax
l
ox
3
ox
l
ox
3
ox
3
(6.046)
As for the remaining three components of zero-order stress, we first
rewrite (6.025) in the form
9
fcc(0) _ .
r
(0) , „
r
(0)
r
(0)
r
(0) ~(0)
Z0^,
-5,,^!
+S
13
7
3
+S
i4
I
4
+S
i5
l
5
+S
l6
l
6
2bSl
0)
>31
J
1
-(0)
2bS^
0)
=s
5l
T
i
(0)
5
33
J
3
s
53
y
3
,(0)
lll'l
TJIJJ,
TSijJi Tj«i(
tl«J,
>34
2
4
s
54"<4
(0)
•,(0)
35'
£
5
.(0)
5
36*6
+
*„rf
)
+^ri
0)
+555
r
5
w
+s
56
r
6
,(0)
(0)
(6.047)
where
5
(Q) _
8u
\
(0)
fix,
j(0)
fix-.
,(0)
——+
-
dx,
dx,
(6.048)
Then, solving (6.047) for r/^, r
3
(0)
and r
5
(0)
in terms of the remaining
quantities, we find
T
(0)
•M
r
(0)
*3
r
(0)
= 2b
= 2b
= 2b
a,<°>
7i\
Ys\
du{
0)
dx,
du[
0)
dx
l
+ /33
+ r$3
duj
0)
dx-,
Sx->
+ /15
+ ^35
+ ^55
-a
ld
ri
0)
-a,^
'14*4
16*6
(0)
- a 7
(0)
- n T
'34*4 36*6
(0)
«54*"
4
(0)
»56
r
6
(0)
(6.049)

Intermediate Approximations 167
where
r
4
(0)
and 7;
(0)
are given by (6.046) and
a
\4
=
T'll^M
+
7li
S
i4
+
^15*54
a
l6
=
?'ll'
y
16
+
^13
5
36
+
J'l5'
S
's6
^34
=
73l
S
l4
+
^33'
S
34
+
^35*54
a
36
=
^31
5
16
+
^33
5
36
+
Y
15
s
56
«54 =r
5
l
5
14
+
r53^34+/55'
S
54
«56=r51^6
+
r
5
3^6+r55'
S
56
(6.0410)
It will be observed that the
a
are constants which couple flexure with
PI
extension.
To obtain
the
displacement-equation
of
motion
we
insert
the
stress-displacement relations (6.044), (6.046)
and
(6.049)
in the
remaining stress-equations of motion
dx
i
dx
z
^
+
^
+
F
2
(0)
=2M*f (6.0411)
dx
x
dx
3
•a
T
(0)
o
r
(0)
fix,
cbc
3
and obtain

168 Mathematical Theory of Vibrations of Elastic Plates
ox, ox:
F)
2
r i F
(0)
h
2
+_*_[
2r
,
5M
,«»
+
(y
I3
+r
55
)«r]
+
4r+V
fixjfixj
r
5
i
2*
or 14
V
fix,
•
+
a,
54
fix
3 7
5
3
M
f
, ^ , „„
x
fi
3
M
f
fix,
3
+ (r
3
.+2
r55
)^-^-
+
3r
:
fi
3
M
f
fix, fix
3
35
fix,fix
3
8
3
u™
3F
3
(1)
dxi
2b'
+
-
a
16
fix,
•
+ a
^^
56
fix
3 7
5
3
"f , „ ,3
3
«f
r
53
-Ti- + (r3i+2
r55
)-
fix,
fix, dx
3
S
3
M
f
+
3
^^3t-
+
^' ,3
5
3
M
f
3F
3
(I)
fix, fix
3
dx{
2b
3
-pu\
0)
Y\\
S
4
M
<
0)
A
5
4
M
f
^ „ fi
4
M
<°> , 5
4
„<°>
fix,
4
fix,
5x
3
fix,
2
fix
2
fix, 5x
3
5
4
M
<
0)
+ r
" fix
4
2Z>
3
/r
2
(0)
+
££j_
+
57?
3
V
fix,
5x
3
i
3
/> v;(0)
V
2
fix. fix,
+
^^3^55)«,
(0)
+
2,
35
<>]
+
4-
+
(0)
b
i r
fix, fix
3
2*
a
54
V
fix,
•
+
or
34
fix
3
7
7 si
5
3
M
f
, „ fi
3
M
<°> , fi
3
M
f
2
- + (r31+2r55)TTf-
+
3
?'35
~
dx
fix,
2
5x
3
fix, fix
3
d
3
u™
3F
3
(1)
2
+
^3 -
3
fix'
2fe
J
+
•
a
56
V
fix
•
+ a
36
fix
3
7
r
53
d
3
u^
t
„ fi
3
«<
0)
+(^31+2^55)
fix' 5x,5x
3
„
5
3
M
f
5
3
i4
0)
3F,
(1)
fix,
5x
3
fix
2Z>
3
=
/*f>
(6.0412)
Equations equivalent to (6.0412) were obtained by Cauchy (1829,
p.
9).

Intermediate Approximations
169
Suppression of the thickness-shear deformation results in a
reduction of the number of edge-conditions sufficient for a unique
solution of the equations. Upon expansion of the terms in the integrand
of the line integral in (5.035) we get
|
(T
(0) .(0)
+T
v> .(0)
+T
(0) .(0)
+r
o, -a)
+T
v^
)ds
(6.0413)
The first two products relate to extension and the last three to flexure.
The term T^u^ *
s not
present because we have set r
4
(1)
and r
6
0)
equal to zero (see Section 6.02). Now, by virtue of
(6.042),
we have
,
1)=
_d^_ (6.0414)
ds
Hence
du™
dT
W
(6.0415)
The term outside the integral vanishes if the traction and displacement
are continuous. Then (6.0413) reduces to
i
r
(0)
ii
(0)
+T
m
ii
m
+ (T<
0)
+^-)4
0)
+T
m
it
m
ds (6.0416)
that is, the three edge-conditions relating to flexure reduce to two
(Kirchhoff, 1850).
If the coupling coefficients (a
pq
) are omitted, (6.0412) separate into
a pair of extensional equations and a single flexural equation (Cauchy,

170 Mathematical Theory of Vibrations of Elastic Plates
1829,
p.
13;
Voigt, 1928, pp. 675-698).
The extensional equations are
8
2
r
n
JT(°)
ox,&
3
26
ox
3
and the associated stress-displacement relations are given by (6.049) with
a
pg
= 0
. In the isotropic case, (6.0417) reduce to the zero-order
extensional equations, i.e., the first and third of (4.043). The relation
between frequency and wave-length is given by the curve marked
"Zero-Order (Classical)" in Fig. 5.072. It may be seen that the
approximation is very good for
a>la>
s
< 1.
The flexural equation is the same as the second of (6.0412). In the
isotropic case this reduces to (Germain, 1821)
DVf«f +2ptaf
=F
2
(0)
+
^J-
+
^2- (6.0418)
dx
x
dx
3
If
we
set the face-tractions equal to zero and
u^ =Asm%x
l
e
il
(6.0419)
