Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.

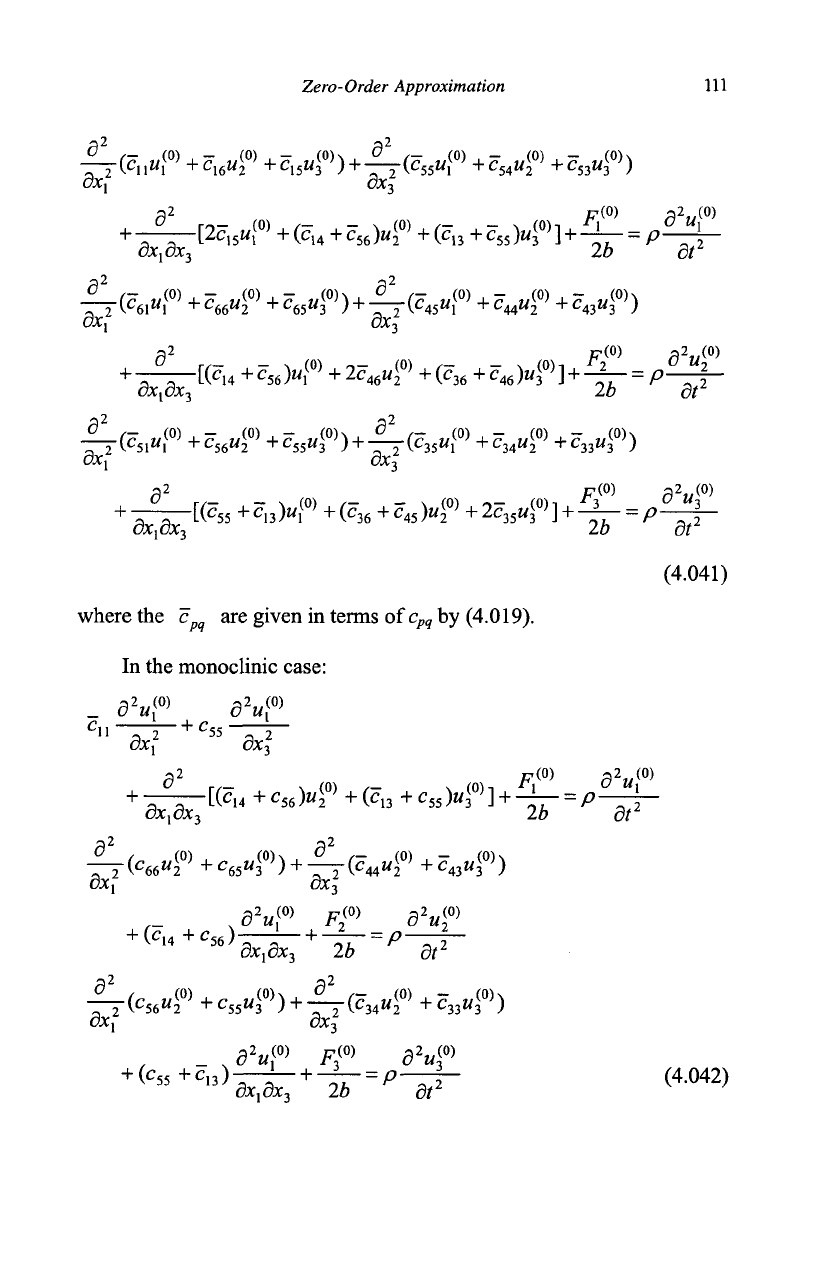
Zero-Order Approximation
111
^(C
U
U^
+
C
16
«f +C
I5
«3
W
)
+
-|i-(c
55
«l<
0
>
+
C
54W
f
+
C
53M3
(0)
)
ox,
ox
3
+ -^—
r2c„
W
,
(0)
+(c
lA +
c^)ui
0)
+(c„+c„)u?
)
^^—
P^A
S2
(C
6
M
0)
+C««f +C„«
3
W)
+
il(c„ll
1
<">
-f^f ^f)
or,
ox
3
+ ^V[(ft4 +^)»,
(0)
+2c
46M
f
+ (c
36
+
c
46
)«f ] + £_
=
,£-£_
ox, ox
3
2b dt
|V(ft.«.
W
+
c
56M
^
+
c
55M
f )
+
|l(c
35
^
+
c
34M
i°)
+
c
33W
f
)
ox,
0X3
fl2
F
(0)
fl
2 (0)
+ 7V^ +^3)11^
+(?
M
+C«)«
2
W
+2C3
5
«<°>]
+
^-
= />^-
x,6x
3
ox,6x,
2b dt
(4.041)
where
the c
p?
are
given
in
terms
of
c
pq
by
(4.019).
In
the
monoclinic case:
2
„(°) P)
2
„(°)
><°> ^
2
„(°)
C
ll J—
+
C
55
T
6x,
dx
3
+ T4"[(C
14
+C56
)
M
f +(?
13 +
C
55
)
W
f
]
+
^
=
P
^i-
ox, 0X3
2o dt
«
2
*.
C
66
M
2
+
C
65
M
3
>>
+
^rYv
C
44
M
2
+
C
43
M
3
/
OX,
OX3
N
o
2
«,
(0)
F
2
(0)
a
2
«f
+ (C,4
+
^56
) ^— + ^T7-
=
/>
—f-
ox^Xj
2b dt
^(C
56
«f
+
C
55
<>
)
+
^(c
3
4
W
f
+
C
33W
3
(0)
)
OX,
OX3
_
N
e
2
w
,
(0)
F
3
(0)
d
2
W
3
(0)
+ (c
55
+ c
13
) —J-
+
^r-
=
P -A-
(4.042)
ox, 0X3
2b dt

112 Mathematical Theory of Vibrations of Elastic Plates
It is to be observed that, in (4.042), c
55
, c
56
and c
66
appear rather than
c
55
, c
56
and c
66
.
For an isotropic plate:
d
2
ul
0)
|
i-vay
o)
Oxf 2 dx
2
i
l
+
vd
2
uj
0)
|
(l-v
2
)F
1
(0)
_p(l-v
2
)aS
(
2 &,5x, 2bE E dt
2
7(0) „
fl2,
f
a
2
M
f
5
2
M
f
F
2
(0)
pd
2
uf
h
+
^-
+
TT—
=
—
f-
(4.043)
fix
2
dx
2
2bn n dt
2
l-v5
2
«f
S
2
«|
0)
dx
2
dx
2
|
i+va
2
»,
(0)
,
(i-v
2
)F
3
(0)
_
/?
(i-v
2
)a
2
»<
0)
2 Sc^ 26F £ dt
2
In all three sets of equations [(4.041)-(4.043)] we have set 6=const.
Equations equivalent to the first and third of (4.043) were obtained
(also as zero-order approximations in a power-series expansion) by
Poisson (1829) and Cauchy (1828) and are commonly called the
equations of the classical (or elementary) theory of extensional vibrations
of thin plates (Love, 1927, p. 497). If the accelerations and face-tractions
are omitted from the first and third of
(4.043),
the two equations become
identical with the corresponding equations of Filon's theory of
generalized plane stress (Love, 1927, p. 138).
4.05 Useful Range of Zero-Order Approximation
The zero-order equations do not contain the simple thickness-modes
and hence are limited to frequencies well below the frequencies of these

Zero-Order Approximation
113
modes. This is to say that the wave-length in the x\ or x
3
direction must
be large in comparison with the thickness of the plate, i.e., #><1. An
estimate of how small the frequency and wave-number must be can be
obtained by a comparison of solutions of the zero-order and
three-dimensional equations. An appropriate solution of the
three-dimensional equations is the one obtained in Section 2.11 for an
isotropic plate. In Section 2.11 we found that, for <f&< 1, the frequency of
the lowest extensional mode is given by (2.1121), i.e.,
fl,=
^hr-2T
(4
-
051)
and the frequency of the lowest flexural mode is given by (2.1116), i.e.,
<° =
?
b
L
2
. (4.052)
V
3/7(1
-v )
To obtain the corresponding solutions of (4.043) we set
u?
"f
= 5sin^x
1
e'
a
"
= 0
Then we find, for the extensional vibrations,
-t\
and for the flexural vibrations
E
p(l-v
2
)
(4.053)
a
=
£\ \
=
HTim
(4
-
054)
\P V
2
P(l + v)
Thus,
the frequency of extensional vibration, obtained from the
zero-order equations, coincides with the frequency given by the exact
equations for very long waves. In the case of flexure, however, the exact
and zero-order equations give quite different results.

114 Mathematical Theory of Vibrations of Elastic Plates
The frequencies are plotted, along with the exact frequencies, in
Figs.
5.071 and 5.072, for
l=2/u.
The ordinate in both figures is
co/co
s
where
i.e., the frequency of the lowest, simple thickness-shear mode.
From Fig.
5.072
it may be seen that the zero-order extensional
equations give satisfactory results for vibrations of the first mode in the
range $><1, i.e., for ratios of half-wave-length to thickness greater than
nil. This is not to say that the zero-order approximation is good for finite
plates whose ratio of face to thickness dimensions is as small as nil,
because the frequency is restricted to the range
co/co
s
<
1
due to the
absence of a second mode in the zero-order approximation. This
restriction confines the usefulness of the zero-order approximation to the
lower modes of thin plates.
From Fig. 5.071 it may be seen that the zero-order flexural
equations are of no value. Hence, in the case of crystal plates in which
extension and flexure are coupled, equations (4.041) are not suitable. For
appropriate equations, see Sections 6.03 and 6.04.

Chapter 5
First-Order Approximation
5.01 Separation of
Zero-
and First-Order Terms from Series
The establishment of a set of approximate equations, in which only
the zero-order and first-order displacements appear, follows a course
similar to that employed in obtaining the zero-order approximation. Thus,
corresponding to (4.011) we begin by setting (see Fig. 3.011)
u\
n)
=
0, ui
n)
=0, n
>
1
(
5011
)
w< >
=0, n
>
2
The retention of u^ is necessary in order to accommodate the
thickness-strains which accompany low-frequency flexure. Consider, for
example, an isotropic plate, in a horizontal position, subjected to simple,
static bending such that the upper face of the plate is concave. Then the
upper half of
the
plate is in compression (in its plane) and the lower half
is in tension. Due to the effect of Poisson's ratio, the upper half must
expand in thickness and the lower half contract. This is a strain of the
nature of S^ (= 2u^, see Fig. 3.032). In addition, if we consider
variation of bending with x\ and x
3
, we see that we must permit the
contributions du^/dx
{
and du^/dx
3
to the strains Sj
2)
and 5g
2)
(see Fig. 5.011).
115

116 Mathematical Theory of Vibrations of Elastic Plates
/
/
A
_c>
V
I
H-
J*>
du
17
du'
17
Fig. 5.011
Strains which are permitted to develop freely in the first-order approximation.
The assumptions (5.011) reduce the kinetic energy-density (3.0514)
to
K=pbufuf
+-pb'ufuf
+
-pb
3
u™u™ +±pb
s
uV>u<P (5.012)
and the strain-energy-density (3.0511) to
U
=•
rhA
X
~>
ftu
m
AyO
P P
dx, dx, dx-,
+
7f
'&U® du?\
dx
l
dx
mm fa?
+ TP —
2
—
3 J
dx,
+
2TiM
2)
+
TP ^2- + TP ^-
i
2
»
2
dx-,
dx,
(5.013)
The presence of uf, 7
2
(0)
, r
4
(0)
and r
6
(0)
in the energies
accommodates motions which represent the three fiindamental
thickness-modes, i.e., the lowest x\ and
x
3
simple thickness-shear modes

First-Order Approximation
117
and the lowest simple thickness-stretch mode (see Figs.
2.031,
2.032 and
3.011). The lowest, symmetric, simple thickness-shear mode (Fig. 2.032,
q=2) is not included; that is, its frequency is assumed to be higher than
that of the lowest symmetric, simple thickness-stretch mode (Fig.
2.031,
p=\).
In an isotropic plate, for example, this limits the applicability of
the extensional equations
to
v<l/3.
The displacement
u^ ,
which
appears in both energies, is associated with the second thickness-stretch
mode (see Fig. 2.031,/?=2, and Fig. 3.011). We choose to eliminate this
mode from the first-order approximation, just
as we
have already
eliminated the third and higher thickness-stretch modes and the second
and higher thickness-shear modes
by the
assumptions (5.011).
To
accomplish the elimination without suppressing z4
2)
completely, we set
in (5.012) and
i<
2)
=0 (5.014)
7-
2
a)
= 7
4
(2)
= 7
6
(2)
= 0 (5.015)
in (5.013). In this way we permit the free development of the first-order
thickness-stretch
( S^
=
2u^ ) and the
portions du^ldx
x
and
du^/8x
3
of
the second-order shears
S^
2)
and S^\ as
shown
in
Fig.
5.011.
As a result of (5.014) the kinetic energy-density (5.012) becomes
K
=
pbitfuf
+
-p^ufuf
(5.016)
In anticipation of an alteration, to be made later, we have identified the

118
Mathematical Theory of Vibrations of Elastic Plates
density, in the first-order kinetic energy, by writing it as p
x
.
As a result of (5.015) the strain-energy-density (5.013) becomes
U
1
3
M
,
(I)
du?
du?
p p
dx, dx-, 9x,
+
T<
0)
dXy 9Xj I 9.X,
(5.017)
while the zero-order and first-order stress-strain relations are
T^=2bc
pq
S^\ p, q = \, 2,3,4,5,6
/>
=
1,3,4,5,6
9 =
1,2,3,4,5,6
(5.018)
where the Sj. ' are given by their full expressions in terms of the
displacements (see Fig. 3.031) but the first-order strains are now
dx,
S^=2u
(
2
2)
s
v
=
M
n
dx-,
S\
l)
=
S?
du
(i)
dx,
du^
Bu\
(i)
+ -
9x, dx
3
dx,
(5.019)
In the first of (5.018) the terms
2b
3
p
dx
3
p
dx
x
,

First-Order Approximation
119
are omitted, as it is desired to permit the free development of these
strains, without contribution to the strain-energy (see Fig. 5.011).
The second and third of (5.018) may be reduced to the single
expression
T*>=h*c„S®
(5.0110)
where
-
C
p2
C
2q
C = C - —
by the same procedure as that followed in the reduction of (4.016) to
(4.019).
In unabbreviated notation, (5.018) become
T
(0) _
lh
„ o(0)
2 (5.0111)
where
C
ijki —
C
ijkl
C
ij22
C
22kt
'2222
The stress-displacement relations are, from (5.0111), (3.037) and
(5.019),
TP=bc
m
(u?}
+
u%
+
8
21
u?
+
5
2k
u?)
i (5.0112)
a -i
v
kl
^
*.' '.*'

120 Mathematical Theory of Vibrations of Elastic Plates
At this stage, the strain-energy-density in terms of the strains is
Then
or
U=bc„SV>Sl°>
+
±b
3
c„SVS?
=
bc
yk!
si?sj!?
+
h%
l
s?s,
(i)
kl
(5.0113)
T
(Q) _ W
p
asf
T
m -
dU
p
ds?
(5.0114)
r
(Q) ^
du
Ij
dS
(0)
'
T(i)
=
i^_
lJ
ds<P
0, i*j
(5.0115)
The zero-order and first-order stress equations of motion (3.0212)
reduce to
7(0) ,
F
(0) _
2bpiij
(0)
TS-Tff+FJO^nii?
(5.0116)
or
