Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Infinite Power Series of Two-Dimensional Equations
81
various orders of approximation and in understanding the implications of
what has been discarded and what retained.
The establishment of plate-equations as early terms in a
power-series expansion of the three-dimensional equations of elasticity
was first accomplished by Poisson (1829) and Cauchy (1828). However,
that was before full use was made of energy and variational methods,
which were introduced in the theory of plates by Kirchhoff (1850). The
method of development of the theory of plates in this and the following
two chapters is a systematic exploitation of
a
combination of the methods
of Poisson, Cauchy and
Kirchhoff.
3.02 Stress-Equations of Motion
We may write, from (1.063), (1.065) and (1.0314),
\
jr
(T
VJ
-pu
J
)&i
J
dV
=
0 (3.021)
The integral is over the volume of the body which, in our case, is
bounded by the surfaces x
2
=+b and a right cylindrical or prismatic
surface 5"(see Fig. 3.061) which intersects x
2
=0 in a curve or polygon C
enclosing an area A. If the plate is multiply connected there are interior
closed curves or polygons C, and A does not include the areas within
them.
Except where otherwise noted, the plate may be of slightly varying
thickness. Thus
b
=
b(x
u
x
3
), — «1, / = 1,3 (3.022)
8x,
On substituting (3.011) into (3.021), we obtain

82
Mathematical Theory of Vibrations of Elastic Plates
\
b
\
A
{T
ijt
-p^ii^iZx-Mpdx.dA
=
0 (3.023)
m n
Now, for /=1 or 3, we write
r*
-b
n
where
rb
-b
are defined as the «
th
order components of
stress.
For i=2,
\
b
T
2j
^
n
2
Sufdx
2
=Y,&
x
2
T
2jt
b
-nl
b
T
2j
x
2
"-»dx
2
}Suy
(3.026)
=2(^
(
"
)
-»^r
,)
)
&
?
)
where
^•"
)=
[^^]-
ft
(3-027)
are defined as the «
th
order components of face-traction. (The first two
orders of
stress
and face-traction are depicted in Fig. 3.021.) Finally,
"
m
" (3.028)
where
=
[2^
+
"
+1
(m + « +
l)-
1
,
m + «even
0, w + « odd
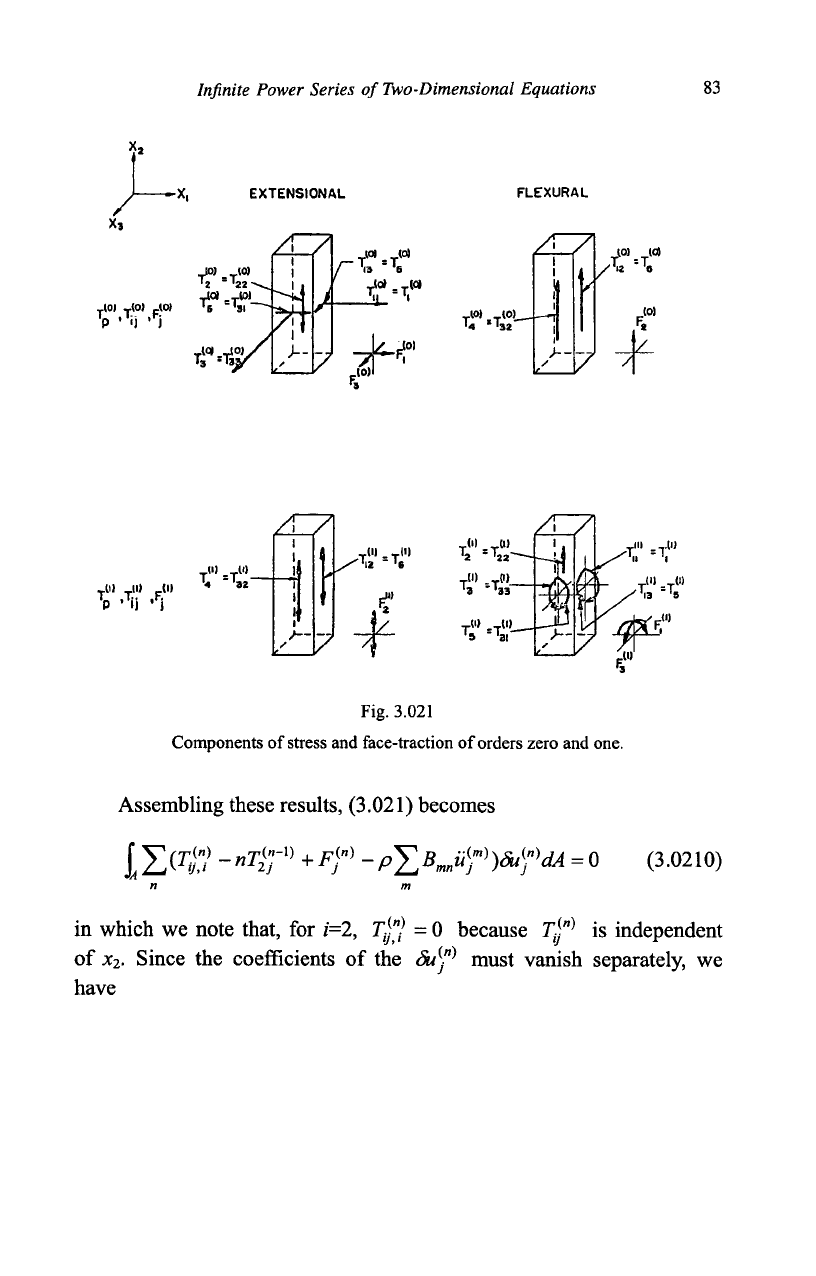
Infinite Power Series of Two-Dimensional Equations 83
X
3
-101 _(0) JO)
'p'
ij • i
EXTENSIONAL
/T7\
JO) (0)
FLEXURAL
_lo) _»>
>-
10) 10)
/•is
=T
«
to)
#
T
W
=T
W
-
—01 _ll) _0I *
32
P • ii ' i
/—
'» 'ai
h7 vti
• • tit m _lLJ
u-
l^'""'
:&>^
f
Fig. 3.021
Components of stress and face-traction of orders zero and one.
Assembling these results, (3.021) becomes
IX^"'
~
nT
V
X)
+F
j
n)
-p
J
Z
B
m
niif)^
(
,
n)
dA
= 0
(3.0210)
n m
in which we note that, for i=2, T$
=
0 because T]j
n)
is independent
of x
2
. Since the coefficients of the du^ must vanish separately, we
have

84
Mathematical Theory
of
Vibrations
of
Elastic Plates
Tff-nTW+F}
H)
=Pl,B
lim
ulj
m)
(3.0211)
which
are the
stress-equations
of
motion
of
order
n. For
example,
the
first four orders
are
-(0)
, ir(0)
T?>+F
W
=p
IJ.I
J "
2b
u?
)
+—^
2)
3 '
J
T}n-n?+Fj
m
=P
26 ..
m
2b ..a)
3
J
5
J
Tff-2Tff
+
F™=p
2b
..
(0)
2b
(2)
v
3
J
5 '
2b
..
(1)
2b ..
(3)
5
7
1
J
(3.0212)
In scalar form the
first
two of these
are
art
0)
97;
(0)
dx,
dx?
•+Fr=p
2bu\
0)
+
2b
5
u\
2)
+-
dT,^ dr,
M2
+ -
(0)
32
dx
l
dx
3
dT\
0)
dT^
+
F.
(0)
2b
3
2bu?
)
+—u?
)
+-
•
+
-
33
7(0)
3x[ 9x
3
+ F
3
W
=^
26*/<
0)
+
3
2b
3
u?+-
(3.0213)
9x,
ar/
2
»
9x,
3^
3r
d)
3x
3
34°
+——
3x
3
.
0i
33
.
r
(0)
F
(D
7
21
+ /
1
2b
..m 26 ../
3)
u\
}
+
u\
}
+••
-T£>+F?>=p
(i)
26 „(n 26
-«<'>
+
dx,
dx-,
•Tg>
+
FV=p
v
26 ..(n
3
3
5
5
26
5
.
«<»+.
«f+••
(3.0214)

Infinite Power Series of Two-Dimensional Equations
85
The left hand sides of
the
first and third of (3.0213) are the usual ones of
Poisson's theory of a thin plate stretched in its plane (Poisson, 1829;
Cauchy, 1828; Timoshenko, 1940, p. 138) or of Filon's theory of
generalized plane stress (Love, 1927, p. 138). The left hand sides of the
second of (3.0213) and the first and third of (3.0214) are the usual ones
of Lagrange theory of flexure of thin plates (Timoshenko, 1940, pp. 86,
87).
Referring to Fig. 3.021 we see that components of face-traction
FJ
n)
are associated with extension wheny'+n is odd and with flexure
wheny'+« is even, just as in the case of displacement wj"\ On the other
hand, the stress 7^
n)
is associated with extension when i+j+n is even
and with flexure when
i+j+n
is odd.
In the abbreviated notation we may write, in place of (3.025),
n
n)
=t^2
(3.0215)
Then (3.0213) and (3.0214) become
Q
T
(0)
dx
x
dT
(°)
dx
x
Q
T
(0)
+
—-—
dx
3
dT
(0)
+ —
3x
3
er
3
(0)
-i—-—
+pr=P
2bii
(0)
2b
2
u{
2)
+-
+ F
2
m
=P
2buf +
fix, dx,
+
F^=P
2biii
0)
+
2b
3
2b
3
;(2)
;(
2
)
+ •••
+
•
(3.0216)

86
Mathematical
Theory
of
Vibrations
of
Elastic Plates
^
'
dT
>
l)
-T™+FV=p
•
+
•
9xj
dx
3
9x,
dx
3
r
(0)
2
2
(1)
_
+
F?'=P
dT
5
w
dx,
Zh—r
4
(0)
+F
3
(1)
=,
dx,
2b
..,t\ lb
u\' +
3
3
2b
3
:;(D
;0>
5
2^
5
26
5
;«
w<
3)
+-
«?>+•
(3.0217)
In
the
notation employed
by
Timoshenko (1940) (except
for the use
of subscripts
1, 2, 3 in
place
of x, y, z and the
adoption
of the
x
2
-axis,
rather than the z-axis,
as the
normal
to the
faces)
we
should write
r
(0)
_
r
(0) _
N
r
(0)
_
r
(0) _
1
2
~
*
22
~~
r
(0)
_
r
(0) _
M
1
3
-''33
_iV
3
r
(0)
_
r
(0) _
n
2
4
~
1
32
-
VS3
T
(0)
_
T
(0) _ )y
1
5
-i,
3
-JV
13
T
(0)
_
T
(0) _
n
F
(0)
r
2
=
1
T
m
=T
m -
M
r(')
-
T(>)
-
1
2
—
J-
22
—
TW=T£=M
3
T
(n _
T
m _
M
-•'32
_
^5
J
13
iw
13
r
(0
_
r
(D _
*6
_i
12
_
3.03 Strain
The expression (1.012) of the strain
in
terms of displacement,
i.e.,
Sy
=^(
u
u
+u
j,d
(3.031)
becomes,
on
substitution of the series-expansion (3.011),
£(*><? +/*
2
-
,
*
2)
;«/"
)
)
+
£(*-«# +nx"i
X
x
u
uf)
(3.032)

Infinite Power Series of Two-Dimensional Equations
87
We write x
2j
—d
2
j and
x
2>
,—S
2i
where, for
k=i
or
j,
[Ik
=
2
8
2k
=\ (3.033)
2k
0, k*2
Using this notation and rearranging terms, we have
S
9
=^kkj
+u
(
fj)
+
ru"
2
~is
2j
u^
+
S
Zi
u^)} (3.034)
In order to define a strain of order n it is necessary that it appears with a
factor x" in the above expression. To this end, we shift terms in the
series to obtain
S
V
=\H
X
2
I"!?
+
U
H
+
(»
+
l
i
S
2j4"
+l)
+
^j"
+l)
)]
(
3
-
035
)
or
•Sj,=2>
2
"4"
)
(3-036)
where
4
n)
=}k"
)
+«5
B
;+(«+ixM"
+,)+
^/«r
)
)]
(
3
-
037
)
are the components of strain of order n. These are illustrated, for orders
zero and unity, in Figs. 3.031 and 3.032, respectively. It will be observed
that, as with stress, a component of strain S^ is associated with
extension of the plate when
i+j+n
is even and with flexure of the plate
when
i+j+n
is odd.
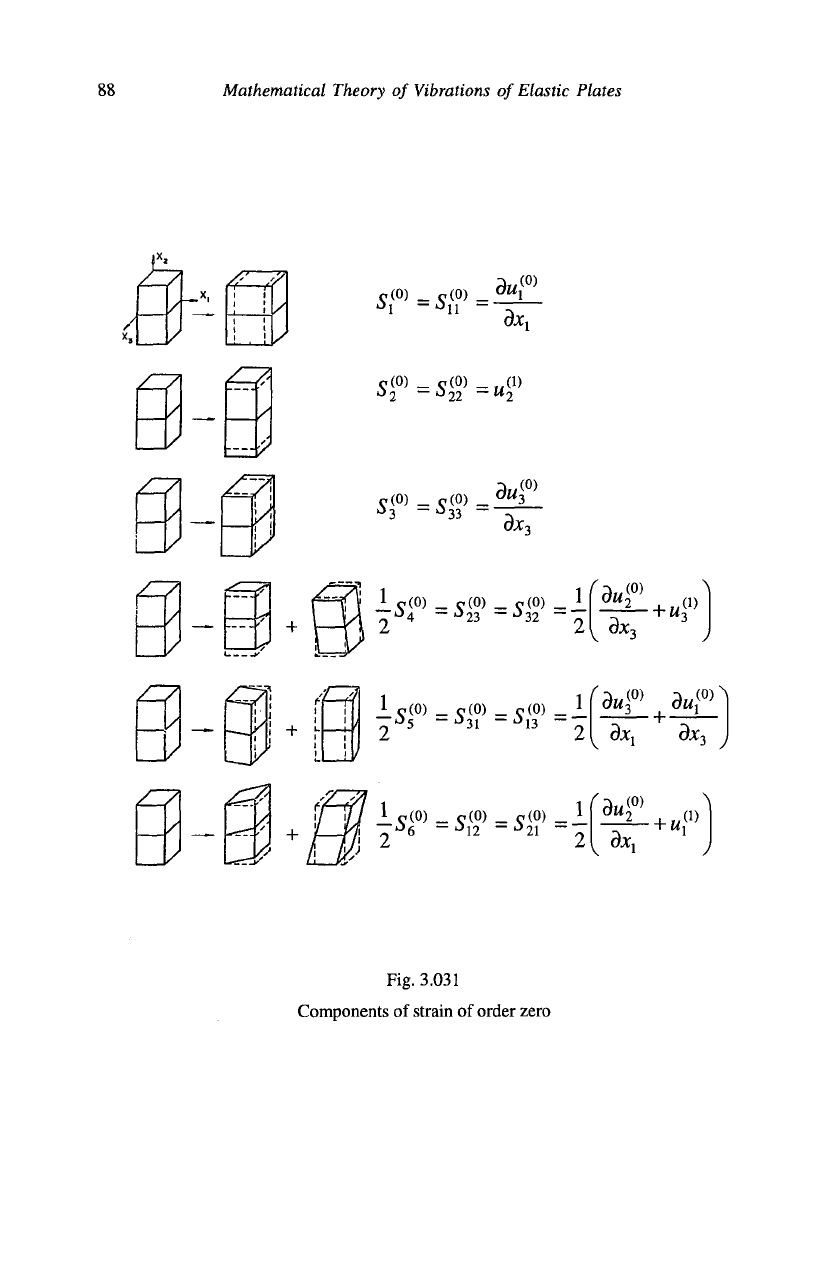
88
Mathematical Theory of Vibrations of Elastic Plates
/?—71
&f—ff
/
$(0) _£«>) _
(0)
11
dx
x
/Z7\
£3\
c(0) _ r-(0) (1)
Jo — O 99 — «0
'22
P
c(0) _ n(0) _
OM
3
'33
dXrt
/£?[
£J\
(Cp\
4&i
1
c(0) _ c(0) _ o(0) _ 1
»23 '32
•
+ u
(1)
1 P(0) _ o(0) _ n(0) _ 1
0
5
- J
31
- J
13
-
^«f>
a
M
,
(0)
'
.
3
^
+
y»
L
v
3*! dx
3
)
1
c(0) _ o(0) _ r,(0) _ 1
—
Of. —On - Jii — _
'12 '21
3*,
•
+ u
(i)
Fig. 3.031
Components of strain of order zero
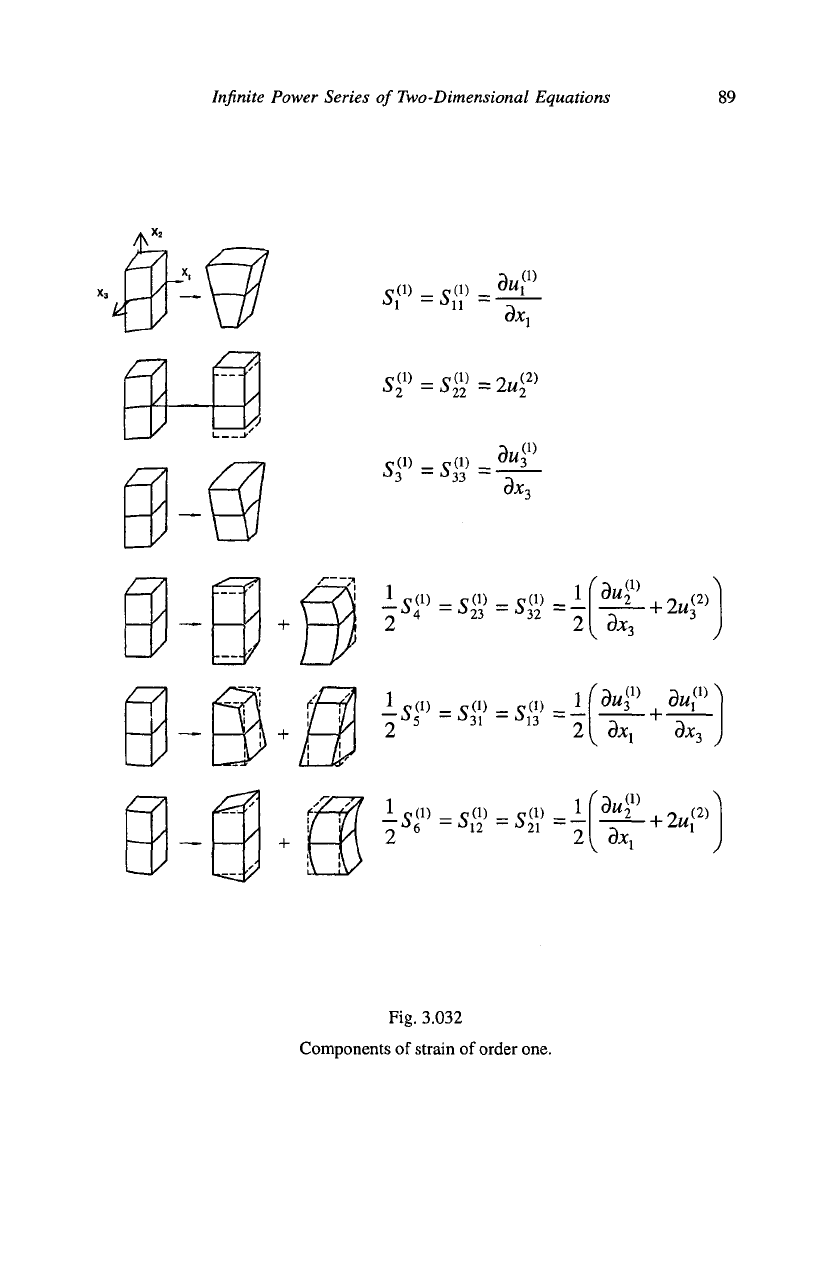
Infinite Power Series of Two-Dimensional Equations
89
PA
PA
V>
PA
PA
PA
cO) _ cd) _
au
l
°1
_0
11 - 2
c(D _ cd) _0„(2)
°2
—
°22 ~ ^
M
2
'(1) _ od) _
'3 - °33 ~'
du
(i)
od) _ cd)
"°4
_
°23
3x,
od) _ 1
^32 ~
2
^
M
(1)
V 3*3
2
+
2«<
2)
1
od) _ od) _ cd) _ *
_ Oc — On —On ~
V
4--^-
J_od) _ PO) _ cd) _ *
o
6
- J
12
-^21 ~ „
ax
x
\
Fig. 3.032
Components of strain of order one.

90 Mathematical Theory of Vibrations of Elastic Plates
In the abbreviated notation (S^), (3.037) becomes
£(-) =
5
(-) = ^1 25g> = 25g> = S<
n)
= ^ + (if + lX"
+1)
ox, ox
3
Sg>
=
Sf
= („ +
1)
M
<"
+1)
2S#>
=
2^3
n)
=
S<
n)
=
M!i + Mil.
ox, 9x
3
0X3 dCj
(3.038)
and (3.036) may be written as
S„=£*2^"\
/>
= l,-,6 (3.039)
3.04 Stress-Strain Relations
The stress-strain relations
T
p
=c
pq
S
q
(3.041)
become, on using (3.039),
r,='
w
I*
2
"S{° (3-042)
n
Then, from (3.0215),
7j-> = \
b
_T
p
x
n
2
dx
2
=0^^ t
b
x
2
+n
dx
2
m
or
n
n)
=c
p
XB
mn
S^ (3.043)
