Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.

Solutions of the Three-Dimensional Equations
61
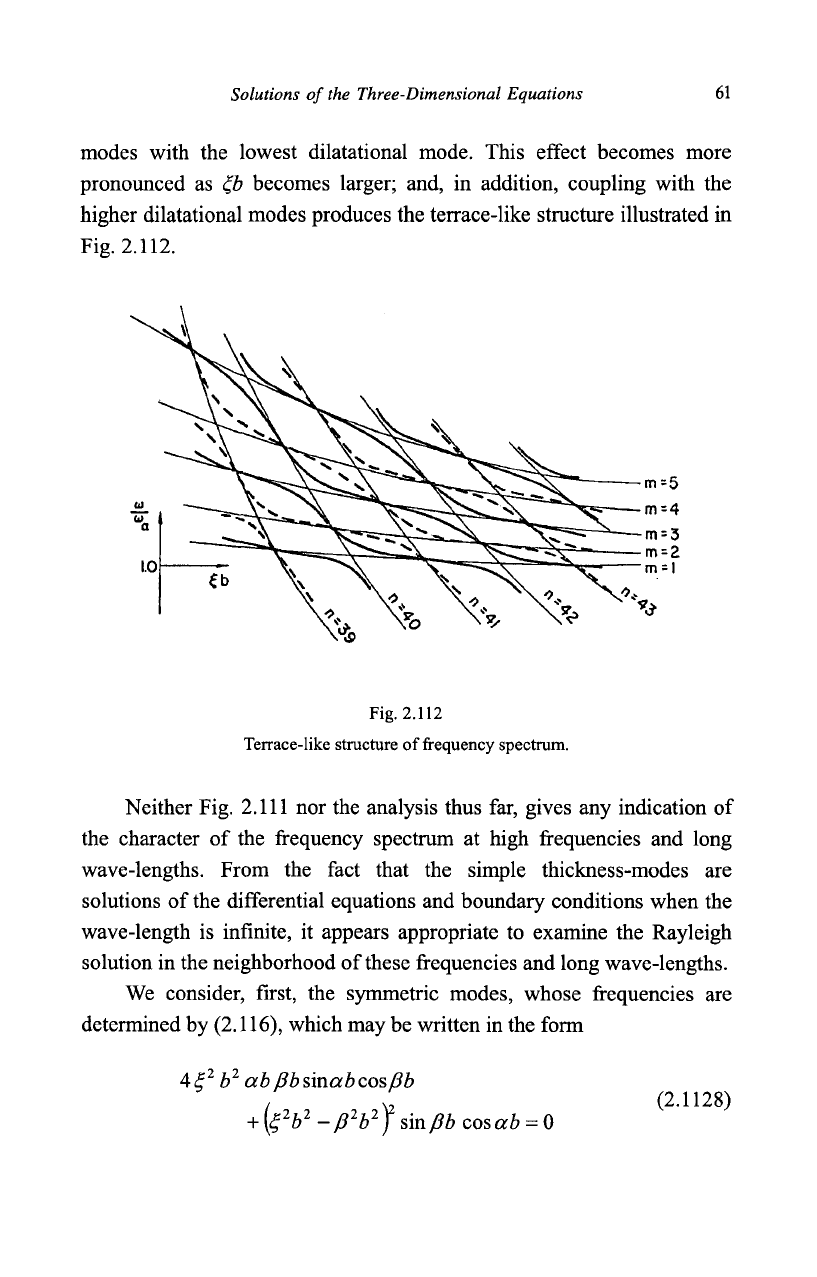
modes with the lowest dilatational mode. This effect becomes more
pronounced as £b becomes larger; and, in addition, coupling with the
higher dilatational modes produces the terrace-like structure illustrated in
Fig. 2.112.
Fig. 2.112
Terrace-like structure of frequency spectrum.
Neither Fig. 2.111 nor the analysis thus far, gives any indication of
the character of the frequency spectrum at high frequencies and long
wave-lengths. From the fact that the simple thickness-modes are
solutions of the differential equations and boundary conditions when the
wave-length is infinite, it appears appropriate to examine the Rayleigh
solution in the neighborhood of these frequencies and long wave-lengths.
We consider, first, the symmetric modes, whose frequencies are
determined by (2.116), which may be written in the form
AE
2
b
1
ab Bb sinab
cos
8b
, \z (2.1128)
+ \?b
2
-
P
2
b
2
[ sin fib cos ab = 0

62
Mathematical Theory of Vibrations of Elastic Plates
where
ab
=
yla)
2
b
2
v;
2
-^
2
b
pb
=
^G>
2
b
2
v-
2
-?b
T-Ul
We seek solutions in the neighborhood
£,b
<
1
and
\{p
+
e)o),,
/7 = l,3,5,...j
K«r +
eK, q
=
2,4,6,...]
' '
where
(2.1129)
(2.1130)
<a
TTV.,
«„ =•
26
(2.1131)
Inserting (2.1130) in (2.1129), expanding the radicals and dropping
products and powers of
<fZ>
and s higher than the second degree, we
obtain
ab-
nn ne c b '
-—
+
—
2 2
/?#
2 £2.2 A
, p
=
1,3,5,.
#;r ^-f c £ b
2 2 qn
r
r
/?*>=
/?;r #£• £6
2J.2 "\
2 2
/OTC
2
(V Jg ?b
2
\
2 2 qn
, ? = 2,4,6,..
, /? =
1,3,5,...
,
?
= 2,4,6,...
(2.1132)
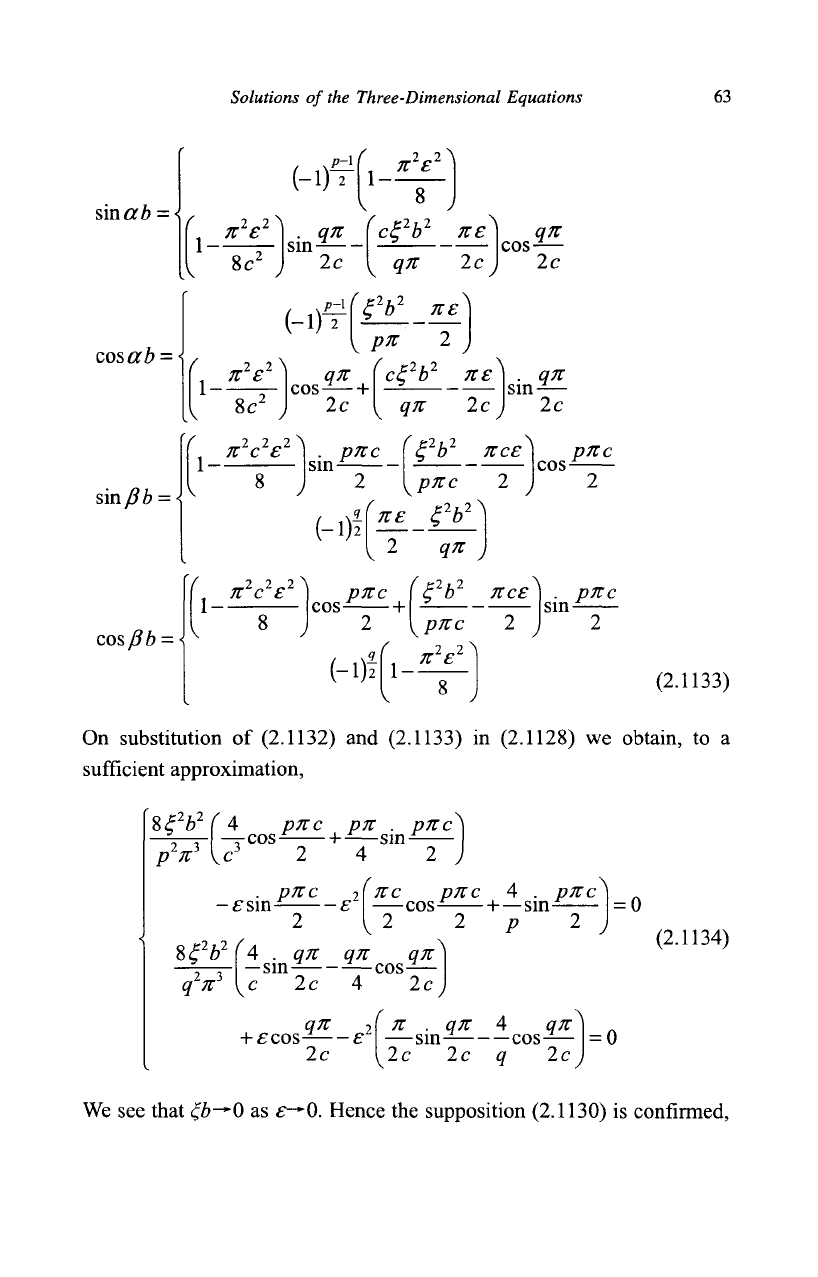
Then, to the same approximation, we find, for/?=l, 3, 5, ..., q=2, 4,
6,...,
Solutions
of the
Three-Dimensional Equations
63
sin a b
=
p-i
(-1)-
2„2A
\
x*e^
v
8c
z
sin
J
qK
~2c
K
£
V
" J
(
_£2L2
cosab
=
(-.)"
9^" 2 c
?b
2
K£
pK
2
COS
qK
~2c
\_n^}
sin Pb
=
Sc'
j
qK
cos
V
2c
( „&l3-
C^
2
b
2
K£
qn
2c
sin
qK
~2c
K
2
C
2
£
2
^
sm
pnc
C
£2,2
pKc
2
cos
/?^c
(-1)"
2
qK
cos J3b
=
f
K
2
C
2
£
2
^
V
PKC
COS
h
^e2.2
J
^b
1
KC£
pKc
2
sin
pKc
(-1)
V^-
n
V
J
(2.1133)
On substitution
of
(2.1132)
and
(2.1133)
in
(2.1128)
we
obtain,
to a
sufficient approximation,
2L2
%?b
p
2
K
3
4
DKC DK . DKC
—rcos-
+
-—sin-
\c
%?b
q
2
K
3
•
PKC 2
-£sin-
£
2
q
2c
4
KC
DKC 4 . DKC
—cos-
1—sin-
2u2
(
4 . qK qK qK^
sin
cos
=
0
(2.1134)
q
K
2
+ £COS-
£
2c
2
Cj
K
. qK 4 qK
—sin- cos-—
2c
2c q 2c
=
0
We
see
that £Z>—0
as
£—-0. Hence
the
supposition (2.1130)
is
confirmed,

64
Mathematical Theory of Vibrations of Elastic Plates
i.e., the limiting frequencies of the symmetric modes, as #>-*0, are the
frequencies of the symmetric, simple thickness-stretch and
thickness-shear modes. We proceed to find the limiting slopes and
curvatures of the curves
co/co
s
vs. gb.
From (2.1130),
£ = i
1 CO
p
cco
s
a>
—q
Hence, for small s, from (2.1134) and (2.1135),
(2.1135)
\6c^b( pn 4 pnc
16£6
?v
qn
T
+—cot-
c
3
2
4 qn
-—tan
J
—
c 2c
(2.1136)
d
2
(<o/co
s
)
dW
16c
16
pn 4 pnc^
-£—+—cot-—
4 c
3
2 y
q n
qn 4 #;r
tan
J
—
4 c 2c
(2.1137)
Accordingly, if
sin^*0,
p
=
1,3,5,.
cos—^0,
q
=
2,4,6,.
2c
(2.1138)
the slopes at £ft=0 are zero and the curvatures are positive or negative
according as

Solutions of the Three-Dimensional Equations 65
pn 4
»;rc>
=—+ -r-cot-— 0
4 c
3
2 <
qn
~~4~
4.
qx>
rk
—tan-— 0
c 2c <
(2.1139)
If, however,
sin = 0
2
cos-—
= 0
2c
(2.1140)
the corresponding curvatures become infinite and the slopes cannot be
determined from (2.1136). In this case, from both of
(2.1140),
we have
c =
jr_ J?
=
2,4,6,...
P |P =
1,3,5,...
(2.1141)
Then, inserting (2.1140) and (2.1141) in (2.1134) we find
d({b)
•
= +-
qn
-, q = 2,4,6,...
(2.1142)
Now, the condition (2.1140), or (2.1141), is the criterion for
coincidence of the frequency of a simple, symmetric, thickness-stretch
mode with the frequency of a simple, symmetric, thickness-shear mode.
Expressed explicitly in terms of elastic constants, we have
U + 2// _ (2(l-v)_ q
' n
V
l-2v ~ p
or

66
Mathematical Theory of Vibrations of Elastic Plates
v =
^4
0.1143)
2(? -P )
For example, v=l/3 when/>=l and
q=2;
or alternatively, when v=l/3 the
lowest symmetric thickness-stretch mode (Fig. 2.031) has the same
frequency as the lowest symmetric thickness-shear mode (Fig. 2.032).
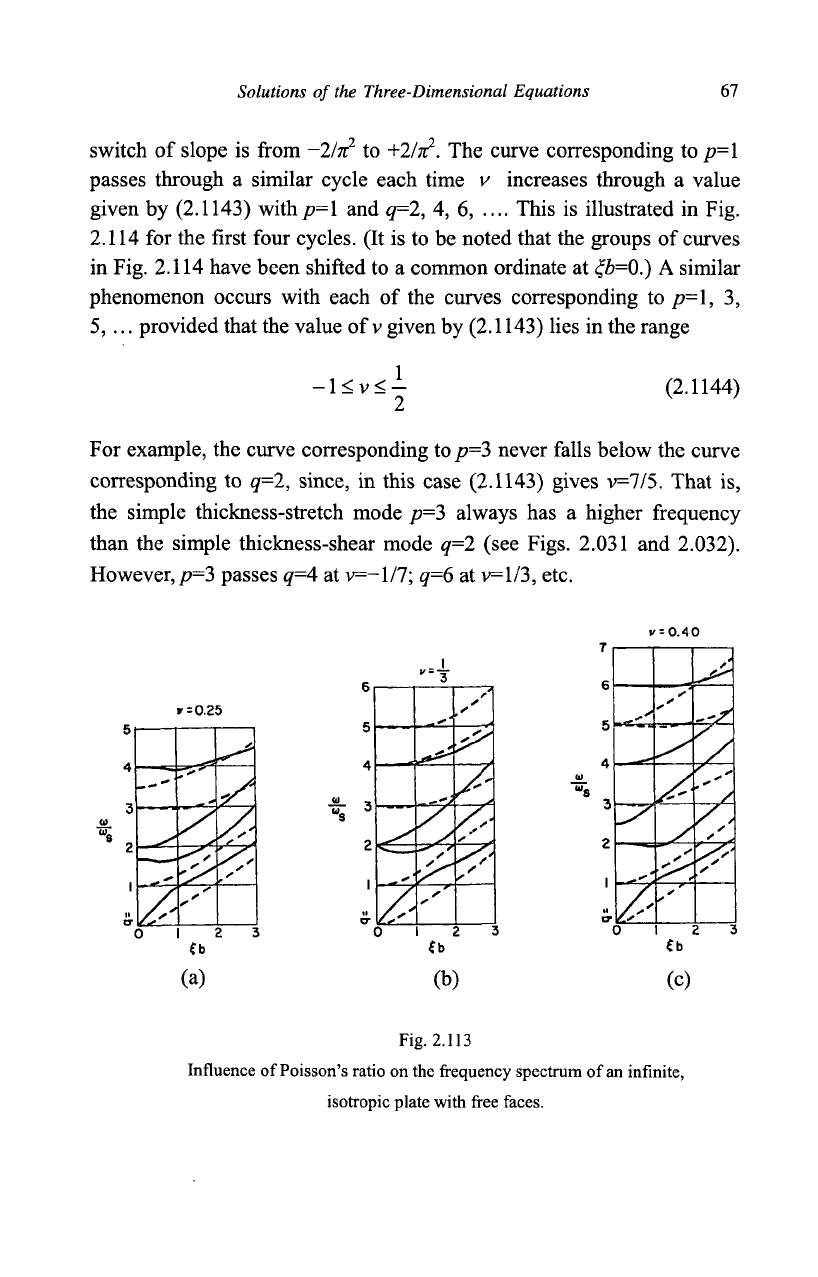
The character of the coupled modes as v passes from below to above
1/3 is illustrated by the heavy, full lines in Fig. 2.113. We shall examine,
in detail, the behavior of the curve corresponding top=l as it rises in the
spectrum with increasing Poisson's ratio. When v=0.25, the curve for the
second symmetric mode in Fig. 2.113(a) approaches
cola>
s
= v3
as £b-*0.
This is the frequency of the symmetric, simple thickness-stretch mode
p-\.
From the first of (2.1136) the slope is zero at gb=0 and, from the
first of (2.1137), with p=\, the curvature at gb=0 is negative. As v
approaches 1/3, the slope remains zero, the curvature approaches
negative infinity and the frequency approaches
a>/co
s
=2,
i.e., the
frequency of the symmetric, simple thickness-shear mode q=2. At
v=l/3,
the slope, from (2.1142), with q=2, is -4/7t
2
. As v exceeds 1/3 the slope of
the curve corresponding top=l switches from -4/%
2
to +4/7i
2
and then to
zero slope and positive curvature. The curve corresponding to p=\ has
now become the third symmetric mode, having passed above the curve
corresponding to the symmetric thickness-shear mode q=2. This is
illustrated, in Fig. 2.113, for v=0.40, for which
co/co
s
is about 2.5 for/?=l
and gb=Q. As Poisson's ratio increases above 0.40, the curve
corresponding to p=\ approaches the curve corresponding to q=4 (at
co/a>
s
=4).
Its slope at £b=0 remains zero, but its curvature diminishes,
passing through zero at v=0.46. (This is the second root of the equation
obtained by setting the first of (2.1137) equal to zero. The first root
occurs at v=-0.5.) Then, as v—7/15 the curvature again approaches
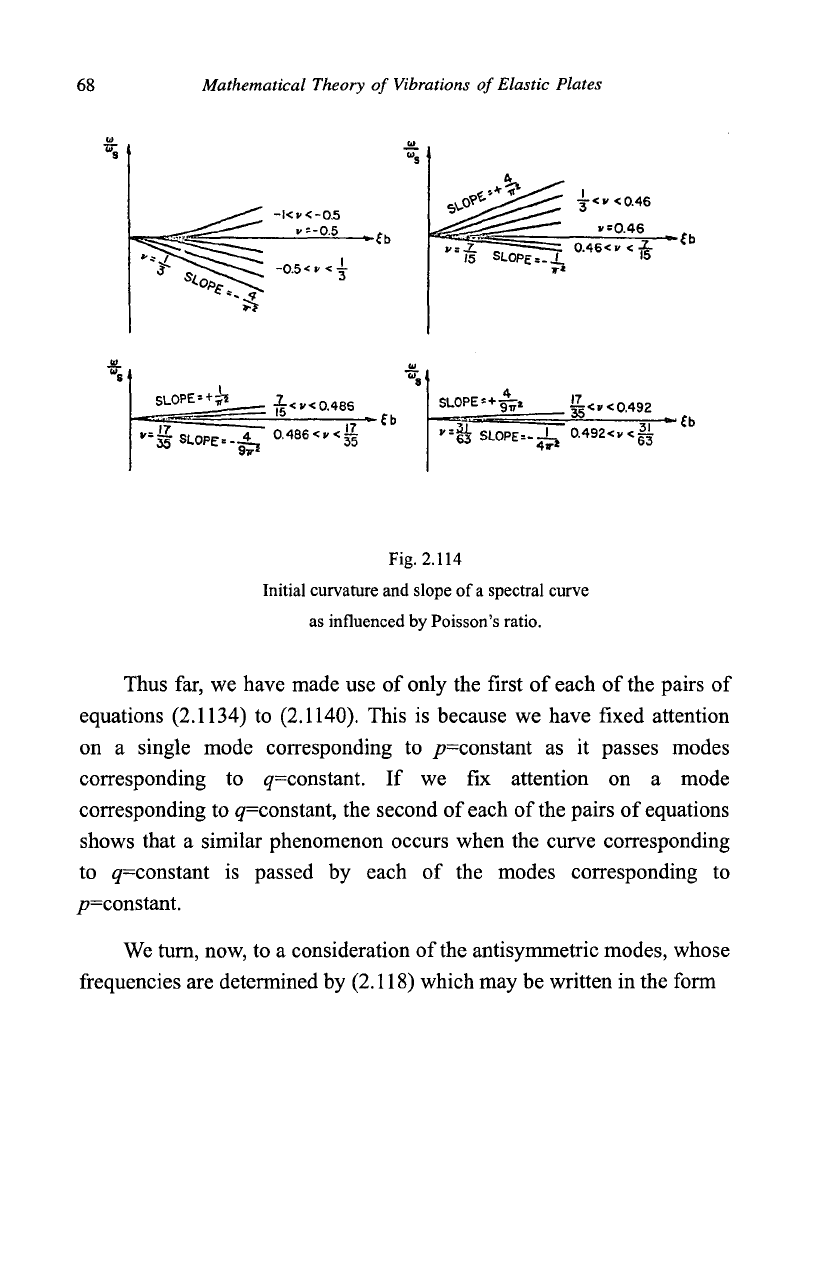
negative infinity and the cycle is repeated as the curve corresponding
to p=\ passes the curve corresponding to q=4. This time, however, the
Solutions of the Three-Dimensional Equations
67
switch of slope is from -21 it
2
to
+211?.
The curve corresponding to p=\
passes through a similar cycle each time v increases through a value
given by (2.1143) with/?=l and q=2, 4, 6, .... This is illustrated in Fig.
2.114 for the first four cycles. (It is to be noted that the groups of curves
in Fig. 2.114 have been shifted to a common ordinate at
£b=0.)
A similar
phenomenon occurs with each of the curves corresponding to p=\, 3,
5,
... provided that the value of
v
given by (2.1143) lies in the range
•l<v<-
2
(2.1144)
For example, the curve corresponding
to p=b
never falls below the curve
corresponding to q=2, since, in this case (2.1143) gives v=7/5. That is,
the simple thickness-stretch mode p=3 always has a higher frequency
than the simple thickness-shear mode q=2 (see Figs. 2.031 and 2.032).
However,
p=3
passes q=4 at v=-l/7; q=6 at
v=l/3,
etc.
v = 0.40
= 0.25
^^ y • s
~"^ ^X^'
r
s^
S *
Cte. 1
I 2 3
;
^: ,
Cell
I 2 3
^£ ^
/ *
IS I
2 3
(a)
(b)
£b
(C)
Fig. 2.113
Influence of Poisson's ratio on the frequency spectrum of an infinite,
isotropic plate with free faces.
68
Mathematical Theory of Vibrations of Elastic Plates
Fig. 2.114
Initial curvature and slope of
a
spectral curve
as influenced by Poisson's ratio.
Thus far, we have made use of only the first of each of the pairs of
equations (2.1134) to (2.1140). This is because we have fixed attention
on a single mode corresponding to /?=constant as it passes modes
corresponding to #=constant. If we fix attention on a mode
corresponding to ^=constant, the second of each of
the
pairs of equations
shows that a similar phenomenon occurs when the curve corresponding
to <7=constant is passed by each of the modes corresponding to
/?=constant.
We turn, now, to a consideration of
the
antisymmetric modes, whose
frequencies are determined by (2.118) which may be written in the form

Solutions of the Three-Dimensional Equations
69
4£ b ab fibsinflbcosab
+
(%
2
b
2
-J3
2
b
2
)
2
sinabcos/lb = 0
This time we seek solutions in the neighborhood £b <
1
and
\{p
+
e)co,,
/>
= 2,4,6,...| , .
[(<7
+ fK, 9 =
1,3,5,.../'
M
ab-
pn ne
E,
2
b
2
^
pn
.2 e2.2
To the second degree in
<^b
and £we find
/>
= 2,4,6,...
9 =
1,3,5,...
/>
= 2,4,6,...
, 9 =
1,3,5,...
qn ne c g b
2 2 qn
0b
=
f
pn_
ne ?b
2
^
2 2 pnc
2
j
qn_
ne 4 b
qn
(2.1145)
(2.1146)
(2.1147)
sina6 =
-
{-l)\
n
2
e
2
^
8c
2
sin
qn
'1c
ne {
2
b
2
^
2 pn
( „fi2.2
c£
2
b
2
ne)
qn 2c
cos
qn
1c
cosab-
(-D
1-
_2„2
N
\
n e
lv
8c
2
qn
cos-—
+
2c
v
u
J
f _£2>2
c^b
2
ne
qn 2c
sin
qn
1c
70
Mathematical Theory of Vibrations of Elastic Plates
s'm/3b
=
1-
2 2 2 A
nee ^
. pne
sin-*-
( £2,2
fb
2
nee
cos pb
=
1-
2 2 2 A
nee
x
(-0
pne
1-
pne
2 2\
n e '
cos
pne
8
V
"J
( £2
7.2
COS
?b
2
nee
pne 2
sin
pne
(-0
qn 2
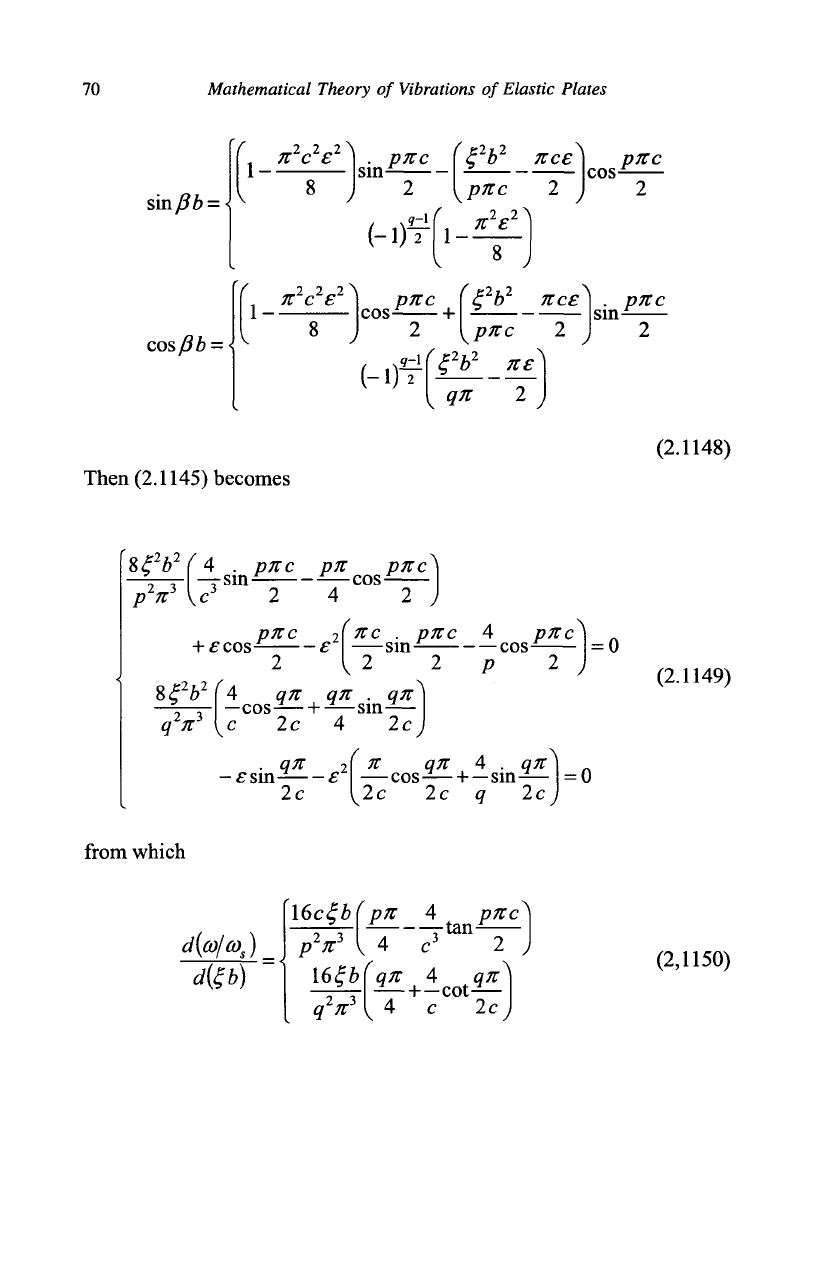
Then (2.1145) becomes
(2.1148)
8<fV
pV
4 . pne pn pne
-^-sin- -—cos-
1
-
Vc
3
2 4 2
pne
2
+ £cos- e
S£
2
b
2r
nc . pne 4 pne
—sin-*- cos-
2 2 » 2
q
2
n>
4 qn qn . qn
—cos-
1
—h -—sin—
c 2c 4 2c
• qn 2
-£sin- e
2c
n qn 4 . qn .
n
—cos-*—h—sin-—
|
= 0
2c 2c q 2c
(2.1149)
from which
d(£b)
\6c£b
p
2
n
3
I6£b
pn
~4~
4 pne
—tan-—
c
3
2
q
2
n
3
qn 4 qn
—+-cot—
4 c 2c
(2,1150)
