Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Solutions of the Three-Dimensional Equations 31
where
c =
pa>
(2.046)
Thus,
modes odd in x
2
are not coupled with modes even in x
2
; but
thickness-stretch and X3-thickness-shear are coupled through the constant
c
2
4- For a non-vanishing solution, the determinants of (2.044) and (2.045)
must vanish:
'24
'24
= 0
(2.047)
or
2c = c
22
+
C44
±
V(C
22
-
C44
)
2
+
4c
2
2
4
(2.048)
Equations (2.044) and (2.045) also yield the amplitude ratios
5,
'24
c-c
44
c-c
(2.049)
22 '24
The equations from which the frequencies are determined are
obtained by substituting (2.043) in the second and third of the boundary
conditions (2.042), with the results
Bj =0, Ajcos7]b
=
0
or
(2.0410)
Aj=0, Bjsm?jb
=
0
These equations have the roots
77
/2b
(2.0411)
where n is an odd integer for modes odd in x
2
and an even integer for
modes even in x
2
. Hence, from (2.0411) and (2.046), the frequencies are
a>
=
-
~2b'
(2.0412)

32 Mathematical Theory of Vibrations of Elastic Plates
where the two values of c are given by (2.048).
If the coupling constant cu were zero the two frequencies would be
(2.0413)
It may be seen, from (2.048), that the larger of these is raised and the
smaller is lowered when c
2
^0.
As an example, we consider the AT cut of quartz, for which
#=35°15'
(see Fig.
1.041).
Then c
22
,
C44
and cu in (2.048) are given by the
second, fourth and eleventh of (1.046), with
0=35°
15'.
Using Mason's
values of c°
pq
as given in (1.047), we find, in units of 10
10
dyne/cm
2
,
c
22
=129.9 c
44
=39.06 c
24
=-5.82 (2.0414)
Then, from (2.048), the two values, say c
2
and
C3,
of
c
are given by
Cl
-= 1.001 p- = 0.995
Thus,
due to the coupling, the higher frequency is raised 0.1% and the
lower frequency is lowered 0.5%. The mode shapes corresponding to
these frequencies may be obtained from (2.043) and (2.049). For
example, the modes odd in x
2
, with n=\, have the shapes
7TX-,
u
2
=
A
2
sin
2b
w, =
A-,
sin —-
3 3
2b
A
2
_
J-15.7,
c
=
c
2
A
3
~ [0.064, c
=
c
3
Thus,
in the mode with the higher frequency, the thickness-stretch
predominates; whereas, in the mode with the lower frequency, the
thickness-shear predominates. The two mode shapes are illustrated in

Solutions of the Three-Dimensional Equations
33
Fig.
2.041.
1-JLJL.J
t
Jl\~
Fig. 2.041
Coupled thickness-stretch and x
3
-thickness-shear
in a simple thickness-mode of a monoclinic plate.
As noted above, thickness-stretch odd in JC2 couples only with
thickness-shear odd in x
2
. However, the former is symmetric, whereas the
latter is antisymmetric, with respect to the middle plane of the plate.
Hence, in a monoclinic plate, symmetric thickness-stretch couples with
antisymmetric thickness-shear. It will be seen, later, that this has an
important bearing on coupling between extensional and flexural
vibrations of plates, inasmuch as the former are essentially symmetric,
and the latter are essentially antisymmetric, with respect to the middle
plane.
2.05 Simple Thickness-Modes in an Infinite, Triclinic Plate
In the case of a plate of general triclinic material, all six elastic
constants in (2.025) and (2.026) are non-zero. As a result, all three
thickness-strains are coupled in each mode of vibration. By the same
procedure as in the preceding section, the frequencies are found to be
(Koga, 1932)
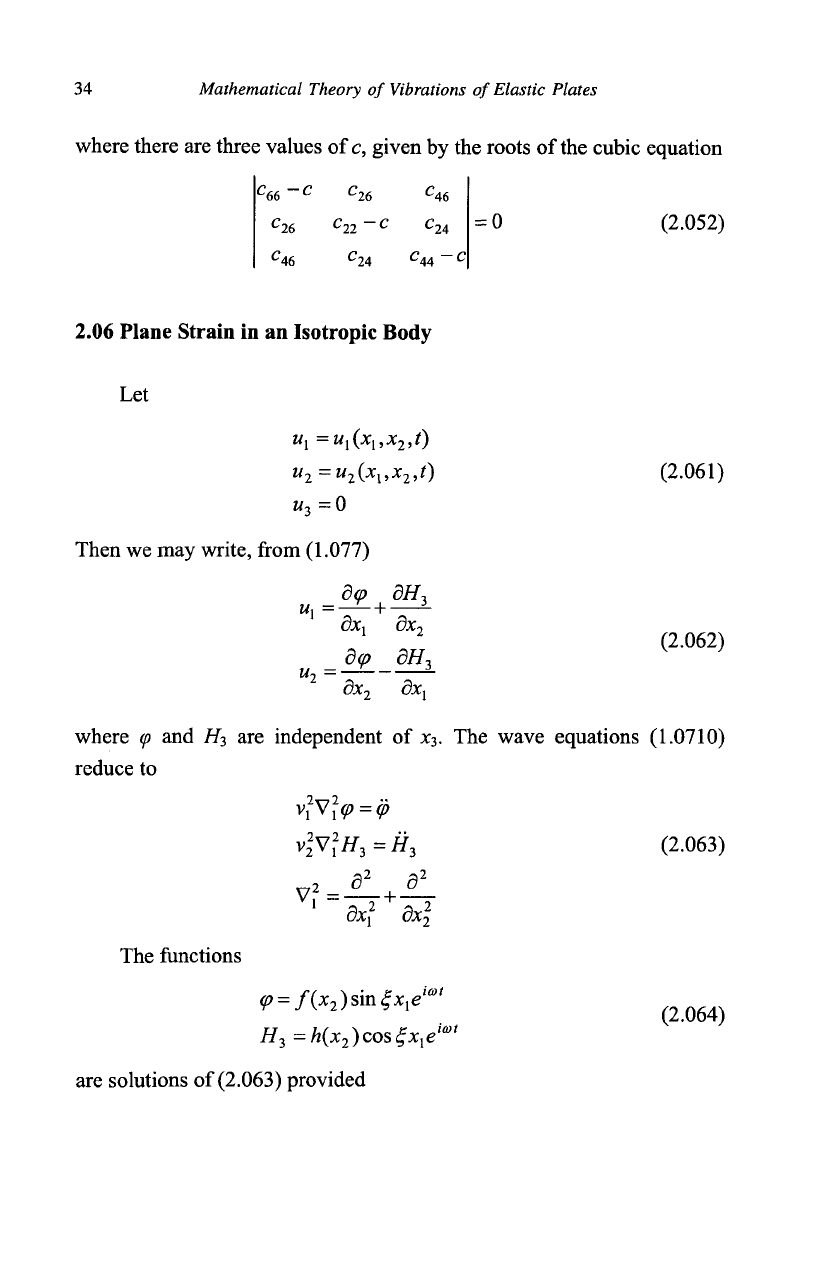
34 Mathematical Theory of Vibrations of Elastic Plates
where there are three values of
c,
given by the roots of the cubic equation
'66 '26
'26
'46
'22
'46
'24
'24
C
AA
~C
= 0
(2.052)
2.06 Plane Strain in an Isotropic Body
Let
Then we may
"i =«i(*i,
M
3
=0
write, from (1.077)
cbt,
w
2
=
cbc,
,X2,t)
8H
3
dx
2
dH
3
dx,
(2.061)
(2.062)
where
<p
and H are independent of x
3
. The wave equations (1.0710)
reduce to
v
1
2
V\
2
H
3
=H
3
(2.063)
The functions
V
-
+
•
dxf dx\
<p =
f{x
2
)sm.^x
x
e"
ot
H
3
=h(x
2
)cos%x
x
e"
are solutions of (2.063) provided
(2.064)

Solutions of the Three-Dimensional Equations
35
h"
+
p
2
h
=
0
where prime denotes differentiation with respect to xj, and
a
2
+C=^
j3
2
+£
2
=o>
Hence
/ = A sin ax
2
+
B
cos
ax
2
h
=
C sin Px
2
+
D cos ftx
2
and
(2.065)
(2.066)
(2.067)
u
:
=(4f+ h')
cos
^
Xl
e
i0
"
u
2
={f'
+
4h)sm%x
x
e
ia
"
T
n
=-M[(fi
2
+ <f -2a
2
)f
+
2£h']sm£x
l
e
ia
"
T
22
= /4(<f -/3
2
)f
+
2£h']sm%x
l
e"
>
" (2.068)
r
33
=
-X{a
2
+Z
2
)fsm%x
l
e
ia
"
T
X2
=ju[2tf'
+
({
2
-p
2
)K\cos^x
x
e
iat
U
3=
T
23=
T
31=°
2.07 Equivoluminal Modes
In the absence of dilatation
(f=0)
the solution (2.068) becomes
w, = h' cos
S,x
x
e"°'
u
2
=^hsin^x
l
e"
01
T
u
=
-
T
ii
=-2ft4h'sm4x
l
e'
a
" (2.071)
T
l2
=^
2
-fi
2
)hcos^
Xl
e""
W
3
=
^23
=
^31
=
^33
=
0

36 Mathematical Theory of Vibrations of Elastic Plates
We note that
T
X2
vanishes throughout if
£
2
=/?
2
,
i.e., if
co =
4lfy
2
=
4lpv
2
(2.072)
Then the only remaining requirement for traction-free faces of the plate
is h'=0 on x
2
=+b. For modes symmetric about the middle plane x
2
=0,
h'
= C/3cosj3x
2
(2.073)
and, for antisymmetric modes,
h'
=
-D/3smpx
2
(2.074)
Hence, 722=0 on x
2
=+b if
P =
nn
/
n
(
2
-
075
)
where n is an odd integer for the symmetric modes and an even integer
for the antisymmetric modes. Then, from (2.072), the frequencies are
a> =
—J—— (2.076)
2b
V
P
The complete solutions are, for the symmetric modes (« odd),
„, „ 2fin
2
n
2
C . nnx
x
nnx
2 icot
T
u
=-r„ =———: sin
L
cos -e
11 22
4b
2
2b 2b
nnC nnx, nnx
7 icat
u, = cos
L
cos -e
1
2b 2b 2b (2.077)
nnC . nnx, . nnx
1 ia>
,
w, = sin
L
sin -e
2
2b 2b 2b
and, for the antisymmetric modes (« even),
Solutions of the Three-Dimensional Equations
37
-Ml
—
^22
—
2/jn
2
7T
2
D . nnx
x
rmx
2
Ab
2
•sin-
2b
-cos-
2b
nnD
nnx,
u,
=
—
2b
nnD
-cos-
2b
sin
nnx
2
nnx,
-sin-
cos-
26
nnx
(2.078)
V"
26 26 26
M
3
=
^23
=
-Ml
=
^33
=
^12 ~0
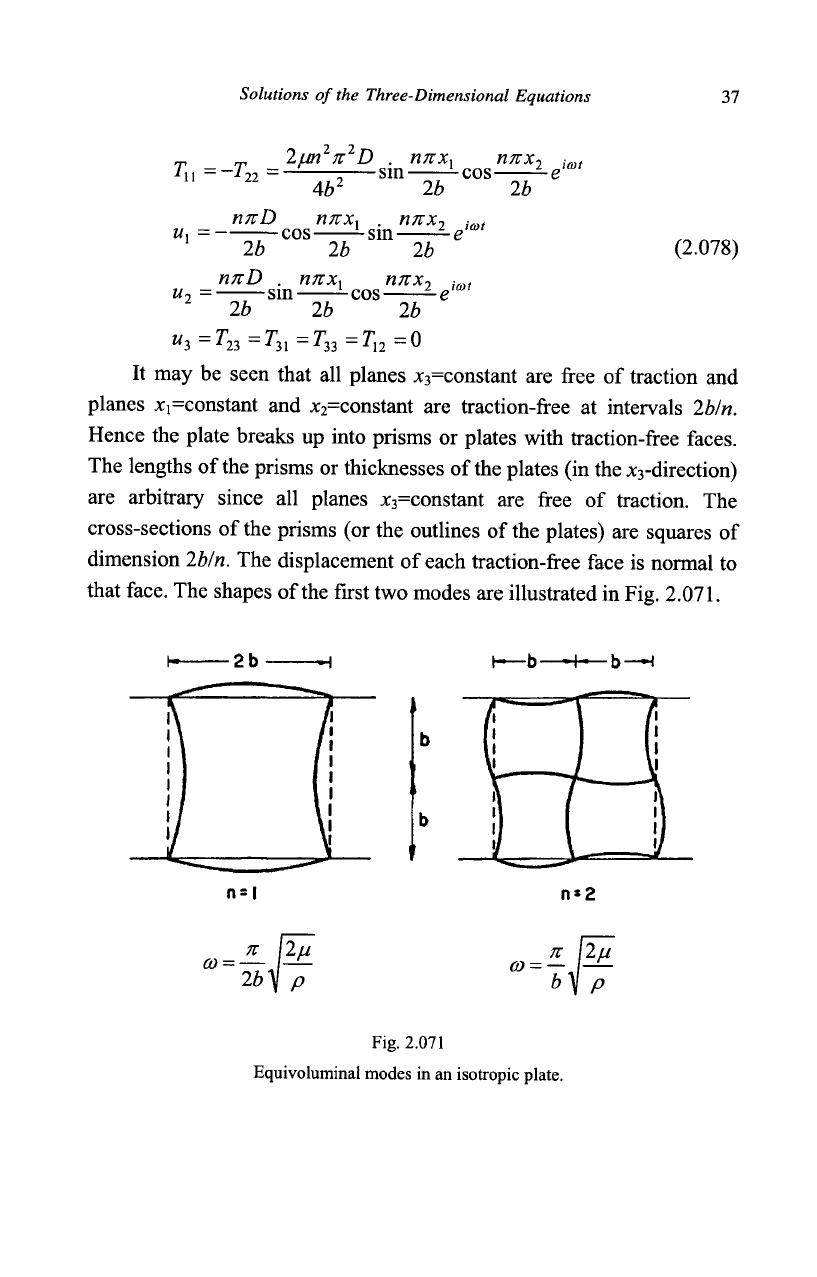
It may be seen that all planes *
3
=constant are free of traction and
planes xi=constant and x
2
=constant are traction-free at intervals
26/H.
Hence the plate breaks up into prisms or plates with traction-free faces.
The lengths of
the
prisms or thicknesses of
the
plates (in the x
3
-direction)
are arbitrary since all planes *
3
=constant are free of traction. The
cross-sections of the prisms (or the outlines of the plates) are squares of
dimension 26/«. The displacement of each traction-free face is normal to
that face. The shapes of the first two modes are illustrated in Fig.
2.071.
2b
n=l
n«2
a>-
£0 =
Fig. 2.071
Equivoluminal modes in an isotropic plate.

38
Mathematical Theory of Vibrations of Elastic Plates
It may be observed that the frequency of the lowest symmetric
thickness-stretch mode is higher than that of the lowest symmetric
equivoluminal mode in the ratio [(k+2fi)/2fi]
m
. However, the frequency
of the lowest antisymmetric equivoluminal mode is higher than that of
the lowest antisymmetric thickness-mode in the ratio 2V2
:1.
The equivoluminal modes described in this section were obtained
by Lame (1866, p. 170). Additional solutions may be obtained by
cyclical permutation of the indices. Linear combinations of these
solutions describe modes of vibration of
a
cube (Sommerfeld, 1947).
2.08 Wave-Nature of Equivoluminal Modes
The vibrations described in the preceding section may be shown to
be composed of four traveling waves. We consider the antisymmetric
modes as an example.
The displacements
u[ = A cos
6
X
sin y(x
l
sin 6
X
- x
2
cos 9
X
- v
2
t)
u'
2
=
Asin0
l
sin^(xj sin^ -x
2
cos^ -v
2
t) (2.081)
u'
3
=0
constitute a wave of amplitude A and wave-number y (=2^/wave-length)
whose wave-normal lies in the xi-x
2
-plane, at an angle 6\ with the jc
2
-axis
(see Fig. 2.081). The direction of the displacement also lies in the
x
r
;c
2
-plane and is at right angles to the wave-normal, i.e., the wave is a
shear wave, or equivoluminal wave. It may be verified that the dilatation
is zero and the displacements satisfy the equations of motion.

Solutions of the Three-Dimensional Equations
WAVE NORMAL
Fig. 2.081
Shear wave u'.
We find, corresponding to (2.081),
V
12
- -Afiysin26
x
cos;K*i sin^ -x
2
cos#
2
-v
2
t)
T[
2
=
-AiJ.yco%2B
x
cosf(x, sin^ -x
2
cos#, -v
2
t)
If #i=7r/4, T[
2
vanishes throughout and, on x
2
=±b,
(2
T'
12
=
-Anycosy
—(x,
+b]yj2-v
2
t
Now consider the wave
u\
=
-A
cos
6
2
sin y{x
{
sin
6
2
+ x
2
cos 6
2
- v
2
t)
(2
u'
2
'
=
A sin
0
2
sin y(x
x
sin
6
2
+
x
2
cos
6
2
- v
2
t)
u
tt
3
=0
40
Mathematical Theory of Vibrations of Elastic Plates
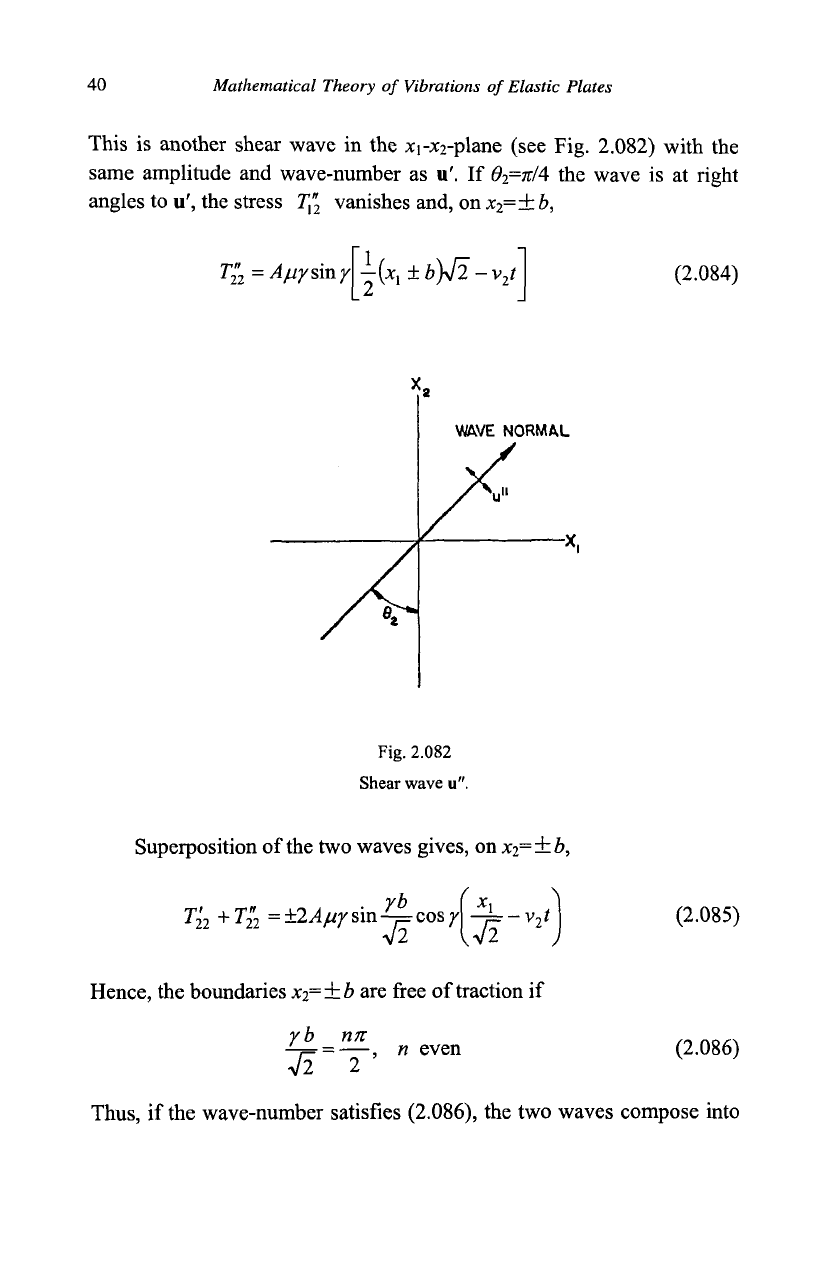
This is another shear wave in the xi-x
2
-plane (see Fig. 2.082) with the
same amplitude and wave-number as u'. If
0
2
=7t/4
the wave is at right
angles to u', the stress T"
2
vanishes and, on x
2
=+b,
Tn=Afiiysiny
-(*,
±b}j2-v
2
t
(2.084)
WAVE NORMAL
Fig. 2.082
Shear wave u".
Superposition of the two waves gives, on x
2
=+b,
T
22
+
T
22
=
±2 Anysinj=
cosy
^= -v
2
t\ (2.085)
Hence, the boundaries x
2
=+b are free of traction if
-
L
j=
=—, n even (2.086)
\2 2
Thus,
if the wave-number satisfies (2.086), the two waves compose into
