Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Elements
of
the
Linear
Theory
of
Elasticity
21
stress-equations of motion (1.015), we obtain
c
IJkl
S
Utl
=puj (1.071)
The strain-displacement relations (1.012) convert these to the
displacement equations of motion
Cijki("k,n
+
u
i,ki)=
2
P
ii
j
(1-072)
In the case of an isotropic material, (1.072) reduces to
M«j.,i +
C*
+
M)«i,,j
=P«J (1-073)
or
//V
2
M/
+(;i
+
J
u)—
=
pu
i
(1.074)
dXj
where V
2
is Laplace's operator and
A
is the dilatation:
d
x,
d x
2
d x
3
. du, du
7
du? .,
n
_
/r
.
A
= ——+ —~
+
T~
(1.076)
d x
t
d x
2
o
x
3
The displacement may be expressed in terms of
displacement-potentials
(p
and H
t
according to
(1.077)
dcp BH,
U
x
=
—?-
+
2--
d
x,
9
x
2
9© dH,
d x
2
d
x
3
a^
a//
2
d x,
d
x,
dH
2
9x
3
a//
3
9x,
a//,
dx-,
provided

22
Mathematical Theory of Vibrations of Elastic Plates
-^-
L
+
-^-
L
+
^—
L
=
0 (1.078)
a
x
x
ax
2
ax
3
Then
Thus,
q>
is the potential which gives rise to the dilatation and the Hj are
the potentials which give rise to the components of rotation. In an
isotropic material, the displacement-equations of motion are satisfied if
the four potentials satisfy the equations (Love, 1927, p. 304; Poisson,
1829,
p. 623)
\ , - (1.0710)
v
2
2
V
2
H
j
=H
j
where
v,=V(/l
+
2//)//>
Y (1.0711)
v
2
=
4^1
P
are the velocities of the dilatation and rotation, respectively.
Equations of the simple forms (1.0710) do not appear to be
available for anisotropic materials except in special cases of high elastic
symmetry (Carrier, 1946).

Chapter 2
Solutions of the Three-Dimensional Equations
2.01 Introductory
In this chapter we consider solutions of the three-dimensional
equations that describe, in closed form, the free vibrations of
plates.
The
aim is to exhibit solutions of the equations for plates with traction-free
surfaces; but other boundary conditions are employed, in certain cases, as
preliminary steps. Most of the solutions pertain to infinite plates. Those
that apply to plates having more than one finite dimension are limited to
specific sequences of dimensional ratios. No solutions in closed form
have been obtained for unrestricted dimensional ratios of plates with
traction-free faces and sides; and none appear to be possible. It is this
circumstance which has led to renewed interest in a method of
approximation which is the subject of the remaining chapters.
2.02 Simple Thickness-Modes in an Infinite Plate
The plate is bounded by the pair of parallel planes
x
2
=
+
b
which are
termed "faces". Simple thickness-modes are defined as those modes of
free vibration in which the faces are traction-free and the components of
displacement are independent of the coordinates in the plane of
the
plate.
Thus
T
2
=
T
4
=T
6
=0 on x
2
=±b (2.021)
23

24
Mathematical Theory of Vibrations of Elastic Plates
Uj=Uj(x
2
,t) (2.022)
In view of (2.022) the strain-displacement relations reduce to
ax
2
S
2
=^
S
5
=0 (2.023)
ax
2
s
3
=o
s
6
=^
9x,
A simple thickness-strain (as distinguished from a thickness-strain)
is defined as one which is independent of
the
coordinates x\ andx
3
. There
are two types: thickness-stretch (£2) and thickness-shear (S
4
, S^)- The
latter two are identified by the designations X]-simple-thickness-shear
(i.e.,
S^) and x
3
-simple-thickness-shear (i.e., S
4
). The simple
thickness-stretch is characterized by displacements normal to the faces of
the plate and the simple thickness-shears by displacements parallel to the
faces of the plate. As will be seen (Sections 2.04 and 2.05) a simple
thickness-mode may contain more than one simple thickness-strain.
When the strains are independent of x
x
and x
3
, so are the stresses.
Hence the stress-equations of motion (1.019), governing simple
thickness-modes, reduce to
dT
6
9x
2
9r
2
9x
2
dT
4
9x
?
d
2
u,
9 w,
=
" a,'
3V
(2.024)

Solutions of the Three-Dimensional Equations
25
and
the
components
of
stress,
appearing
in
these equations,
are
related
to
the displacements, according
to
(1.041)
and
(2.023),
by
_ dw
2
du
3
du
x
If, — Clf.
~Z
r CAC. — r C,
6 ~
u
26 -, ^ M6 -, ^
c
66 ->
a
x
2
dx
2
dx
2
T
2
=c
22
^
+
c
24
^
+
c
26
^-
(2.025)
dx
2
a x
2
dx
2
du
2
du
3
d
u
x
T
•"
C44
— I"
C
46
—
a
x
2
a x
2
dx
2
T
4
—c
24
+
c
44
+ c
46
Substituting (2.025)
in
(2.024)
we
find
the
differential equations
governing
the
simple thickness-modes:
a
2
, x a
2
«,
(c
66
w,
+c
26
u
2
+ c
46
u
3
) = p
dx
2
dt
-\2 -\2
(c
26
u
l
+c
22
u
1
+c
24
u
3
) =
p r
2
-
(2.026)
d
2
, v d
2
U,
——
{c
46
u
x
+c
24
u
2
+c
44
u
3
)
=
p~f
dx
2
dt
2.03 Simple Thickness-Modes in an Infinite, Isotropic Plate
When the material of the plate is isotropic,
c
24
—
C
46
—
C
62
—
0
(2.031)
c
22
=Z
+
3/i,
c
44
=c
66
=//
and
the
equations
of
motion governing
the
simple thickness-modes
(2.026) reduce
to

26
Mathematical Theory of Vibrations of Elastic Plates
d
2
U, 3
2
M.
"j-ri~
=
P-T^> 7 = 1,2,3 (nosum) (2.032)
dx
2
dt
where
c, = c
3
=
ju
,
c
2
=A
+
2{i (2.033)
Assuming a time-factor e"
ay
, omitted in the sequel, we find
a
2
«..
£ +
TIjUj=0
(2.034)
9x^
where
j]j=pcoj/c
j
(2.035)
The solutions of (2.034) are
w
;
- =
^4 •
sin
rjj
x
2
+
Bj
cos rjj
x
2
(2.036)
in which
Aj
and Bj are constants.
The boundary conditions (2.021) reduce, in the isotropic case, to
-^- = 0 on x
2
=±b (2.037)
dx
2
or
± Aj
r\j
cos
r\j
b +
Bj
r\j
sin i]jb
=
0 (2.03 8)
The solutions of (2.038) are
Bj=0, 7jj=r7r/2b, r =
1,3,5,-
(2.039)

Solutions of the Three-Dimensional Equations
27
and
Hence
Aj=0, T}j=rx/2b, r
=
2,4,6,—
(2.0310)
w,=^,sin -, r odd
11
2b
w,=5,cos -, r even
1 J
2b
(2.0311)
and the corresponding frequencies are, from (2.035),
(2.0312)
For convenience, we let
r=p
for the thickness-stretch modes and r=q
for the thickness-shear modes. Then the odd orders of thickness-stretch
designate vibrations symmetric with respect to the middle plane of the
plate and the even orders of thickness-stretch designate vibrations
antisymmetric with respect to the middle plane. Conversely the odd and
even orders of thickness-shear are the antisymmetric and symmetric
modes, respectively. Thus the frequencies are given by
/>
= 1,3,5 (symmetric thickness-stretch)
p = 2,4,6
• • •
(antisymmetric thickness-stretch)
q
=
1,3,5
• • •
(antisymmetric thickness-shear)
q = 2,4,6 (symmetric thickness-shear)
(2.0313)
The shapes of
the
first few modes and the associated frequencies are
shown in Fig. 2.031 for simple thickness-stretch and in Fig. 2.032 for
simple thickness-shear. It will be observed that p or q identifies the
number of nodal planes parallel to the faces of
the
plate.
pn
C0=J
—
t
2b
1
qn
co =
-—,
2b\
lA
+ 2ju
a
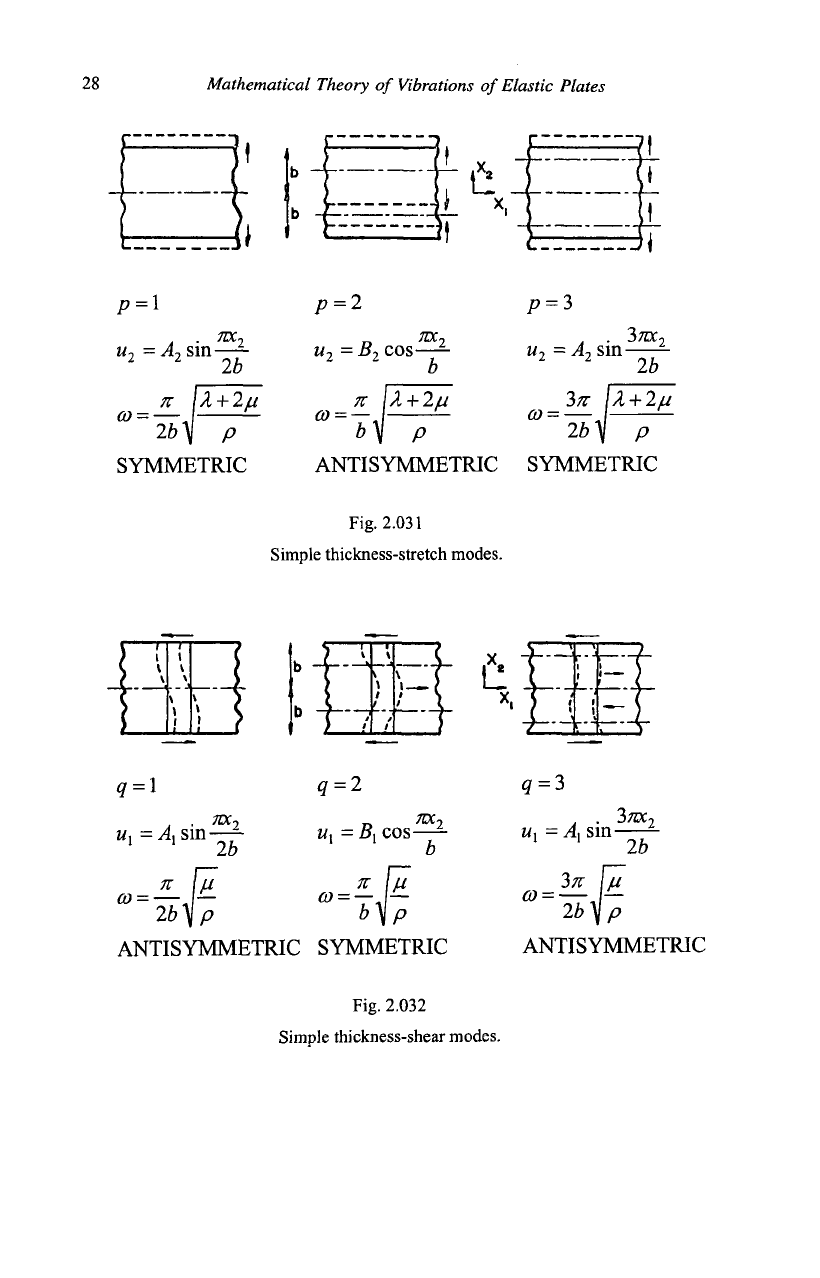
28 Mathematical Theory of Vibrations of Elastic Plates
it
t3
u-y - A-, sin—-
2 2
2b
co-
n
\A,
+ 2p
~2b~i
p
SYMMETRIC
p = 2
7DC
2
u-,
= B
?
cos—-
2 2
6
7T IA + 2p
co = — A —
b\ p
. . 3TEX,
u-,
= A
7
sin-
26
<y =
3;r \A + 2p
lb~V p
ANTISYMMETRIC SYMMETRIC
Fig. 2.031
Simple thickness-stretch modes.
q = \
w, =
A,
sin
:
TDC.,
2b
n p
co
=
—J—
2b\p
q = 2
u> =
B,
cos—-
b
l
\
'V
11 p
co = — , —
b\p
ANTISYMMETRIC SYMMETRIC
q = 3
. . 3nx
?
w, = A, sin-
2b
co =
In \p
2b \p
ANTISYMMETRIC
Fig. 2.032
Simple thickness-shear modes.

Solutions of the Three-Dimensional Equations 29
The antisymmetric mode of lowest frequency is always the
thickness-shear mode q=\. The next higher antisymmetric frequency may
be that of the first antisymmetric thickness-stretch mode (p=2) or the
second antisymmetric thickness-shear mode (#=3), depending on the
value of Poisson's ratio. These two modes have the same frequency when
v=l/10.
Generally, Poisson's ratio is greater than 1/10 so that the second
antisymmetric mode is usually the second thickness-shear mode. In any
case,
the frequency of the second antisymmetric mode is between 2V2
and 3 times the frequency of
the
first antisymmetric mode.
In the case of the symmetric modes, the thickness-mode of lowest
frequency may be either the first symmetric thickness-stretch mode (p=l)
or the first symmetric thickness-shear mode (q=2) according as
v%l/3.
For values of Poisson's ratio commonly encountered, the frequencies of
these two modes may be close together.
Coincidence of frequencies of simple thickness-modes occurs when
p
2
(A
+
2{i)
=
q
2
{i (2.0314)
that is, when
V =
J-Z*£—
(2.0315)
2(q
2
~p
2
)
This phenomenon has an important influence on the character of
the frequency spectrum of more general vibrations (see Section 2.11)
and, accordingly, affects the formulations and ranges of usefulness
of approximate equations of high-frequency vibration of plates (see
Chapter 5).
2.04 Simple Thickness-Modes in an Infinite, Monoclinic Plate
When the material of
the
plate has monoclinic symmetry, with x\ the
two-fold axis, C46=c
2
6=0. Then the differential equations (2.026) reduce

30
Mathematical Theory
of
Vibrations
of
Elastic Plates
to
and,
C66
dx\ ~
P
dt
2
d
2
u
2 i
d
2
u
3
^22 i ^24 1 —
dx
2
dx
2
d
2
u
2 t
d
2
u
3
24 i ^44 •} —
dx
2
dx
2
d
2
u
7
d
2
u
3
from (2.025), the boundary conditions, on x
2
z
dx
2
du
2
9w
3
C
22 -
+C
24 -
ox
2
ox
2
du
2
du
3
C
24 -
+C
44 «
ox
2
ox
2
= 0
= 0
=±b,
reduce to
(2.041)
(2.042)
Thus,
the xpthickness-shear strain is not coupled with the other two
either in the differential equations or the boundary conditions. Hence the
mode shapes and frequencies of Xi-thickness-shear are the same as in the
isotropic case (Section 2.03) with the exception that
pt
is replaced by c
66
.
To find the shapes and frequencies of
the
remaining modes, consider
solutions of
the
form
Uj
=
Aj sin
rjx
2
e
icot
+
Bj cos rjx
2
e
ia
", j
=
2,3 (2.043)
Substituting in the second and third of
(2.041),
we find
(c
22
~c)A
2
+C
24
A
3
=0
c
24
A
2
+(c
44
-c)A
3
=0
and
(2.044)
(c
21
-c)B2+c
24
B
3
=0
C
2
4
5
2+(
C
44-
C
)
5
3
=0
(2.045)
