Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates
Подождите немного. Документ загружается.


Elements of the Linear Theory of Elasticity
11
C
15
_
C
16
~~
C
25
_
C
26
_
C
35
~
C
36
_
C
45
_
C
46,
_
"
(1.042)
Then
(1.043)
7,
—
c,, o, +
c
12
o
2
+
c
13
5
3
+ c
14
o
4
-* 2
= C
21 "1
+ C
22 "2
+ C
23 "3
+ C
24 "4
xi
—
^31
*^1
32 2 31 3 34 4
T
4
= c
41
5, + c
42
S
2
+
c
43
5
3
+ c
44
5
4
^5 -
C
55 ^5 +
C
56 ^6
^6
= C
65 ^5
+ C
66 ^6
In the trigonal, if
x^
is the trigonal axis and x
x
a binary axis, we have,
in addition to (1.042),
(1.044)
c
34
—
0, c
24
—
c,
4
, c
n
—
c
22
, c
2
i
—
c
13
C44=C
55
,
C
i6
=C
u
,
C
66
=— (C,,
—
C
X1
)
so that there are six independent constants. Then
T
x
- c,, 5, +
c
12
5
2
+
c
13
iSj
+ c
14
5
4
^2
=
C
21 "1
+
C
l
1
"2 +
C
13 ^3
—
C
14
^4
T
3
=
C
31
5,
+
C
31
5
2
+
C
33
0
3
r
4
=
C4
,5,-c
14
5
2
+
C44
5
4
(1.045)
T
5
- c
M
S
5
+
c,
4
S
6
^6 -
C
14 ^5 + T (
C
l
1
- C
12 ^
In the case of quartz, which belongs to the trigonal system,
X\,
x
2
,
x-$
are the electrical, mechanical and optical axes, respectively (Mason,
1946,
p. 28). Let us designate these axes as x,°, x\, x°, respectively
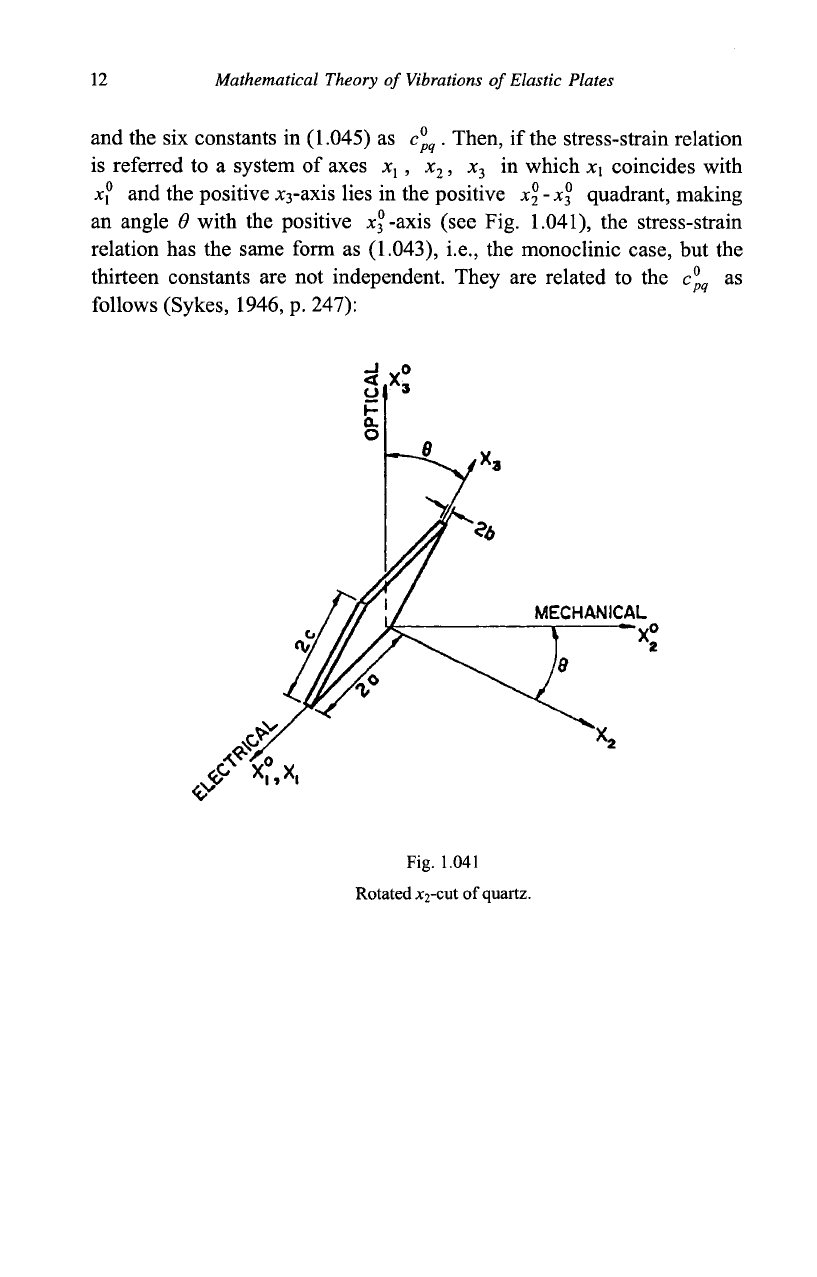
12
Mathematical Theory of Vibrations of Elastic Plates
and the six constants in (1.045) as c°
pq
. Then, if
the
stress-strain relation
is referred to a system of axes x
x
, x
2
, x
3
in which x
x
coincides with
x° and the positive x
3
-axis lies in the positive x\
- x°
quadrant, making
an angle 6 with the positive xj-axis (see Fig.
1.041),
the stress-strain
relation has the same form as (1.043), i.e., the monoclinic case, but the
thirteen constants are not independent. They are related to the c°
pq
as
follows (Sykes, 1946, p. 247):
Fig. 1.041
Rotated x
2
-cut of quartz.

Elements of the Linear Theory of Elasticity
13
c
l
1
~
c
l
1
C
22
= C
l
1
C
"*"
C
33 * "*"
2(2
cl
+
c°
u
)s
2
c
2
+
4
c°
4
sc
3
c
33
=
c,°,
s
4
+
c
3
°
3
c
4
+
2(2
c°
44
+
4 )s
2
c
2
-
4
c°
4
s
3
c
c
44
= 4 + (cf, + 4 - 4
c
4
°
4
-
2
Cl
°
3
)s
2
c
2
-
2
4
(c
2
-
j
2
)s c
0 2 , 0 2 , r. 0
c
55
=c
A4
c +c
66
s +2c
u
sc
_ 0 2,0 2_T0
C
66
—
C
44 *
+
C
66
C
^ C
14
J C
„0 2 , 0 „2
c
12
= 4 c
z
+ 4 5-2 4 s
c
(1.046)
Cti — ^19 " 1 ^ ^14 " ^
0^2 2V f 0 0 ^
C
14
=C
l
4
l
C
~S )+{Cl2-Ci
3
)SC
c
23
=c,
0
3
(c
4
+/)+(c
1
°
1
+4 -4c
4
°
4
y
c
2
-2c,°
4
(
C
2
-s
2
)sc
c
2A
=cl(As
2
-\)C
2
+ [C,V
2
-C3V
2
-(2C
4
°
4
+
Cl
0
3
)(c
2
-,
2
)],C
C34
=
-C,
0
4(4C
2
- l),
2
+ [
C
,V
2
-
C
3
V
2
+
(2C
4
°
4
+ &\c
2
S
2
)]SC
C
56 =
C
1°4
(c
2
- S
2
)+
(c
6
°
6
- C44 )s C
where ,y=sin#, c=cos#.
;s ui C
10
1U
dyne/cm",
The values of c for quartz (Mason, 1950, p. 84) are, in units of
10 1 ,/„
m
2
4=86.05
c}!,
=18.25
„0 _
A
or „0
4=4.85 4=107.1 (1.047)
4=10.45 4=
58
-
65
In the case of an isotropic material (2 constants) the stress-strain
relation reduces to
14 Mathematical Theory of Vibrations of Elastic Plates
i
2
=
c
21
S, + c
n
o
2
+
c
12
o
3
*3 =
c
2l
S
{
+
c
2l
S
2
+
c
n
o
3
^4
=
TV
C
11
_C
12/^4
^5
=
TV
C
11
-C
12)^5
*6
=
:i"l
c
ll
_C
12A>6
(1.048)
The relations of the constants c\\ and c
i2
to Lame's constants
(X,
/x)
and to
Young's modulus, E, and Poisson's ratio, v, are given in Table 1.041.
Cll
Cl2
Table 1.041
Elastic Constants of Isotropic Materials
Cn, c
l2
cn
C\l
C\2
k,fi
X+2/u
X
X
c
ll
-c
12
E,v
(l + v)(l-2v)
Ev
(l + v)(l-2v)
Ev
(l + v)(l-2v)
E
M
2
M
2(1+ v)
(c
11
+2c
12
)(c
1
|-c,
2
) fi(3A + 2/i)
c
u
+c
i2
A
+
n
c
\2 h
cn
+c
i2 2(A
+
ft)

Elements
of
the Linear Theory of Elasticity 15
1.05 Uniqueness of Solutions
Subject
to
certain restrictions, initial
and
boundary conditions,
sufficient to assure
a
unique solution of the stress-equations of motion,
may be obtained from Neumann's theorem (Love, 1927, p. 176).
In
a
body occupying
a
volume V, bounded by
a
surface S, consider
two sets
of
displacements, strains, tractions and stresses and
let
their
respective differences be designated by starred symbols. Also, let K* and
U* be the
kinetic
and
strain-energy-densities calculated from
the
difference-displacements and difference-strains and let
K* and
U*
be
the total kinetic and strain-energies
of
the body, calculated from the
difference-energies and reckoned from an initial time
to
to
a
later time
t.
Then, the total energy in the body at time t is
K*+U*=K*(?
0
)
+
U*0
0
)+
\'dt\
(k'+U')dV (1.051)
where K*(^
0
)
and
U*(?
0
) are the initial values
of
K*
and U*.
Now
0'=^S;=T;S;=T;JUI
=
(
T
vUj),i-Ti*j,i«*j
and, by the divergence theorem,
J>i>;)
f
^= frXjii-j dS=\/ju) dS
(1.052)
Also,
£r*
1
B
( ., .
t
\ ... .»
2
dt
K J jJ
'
J
Hence

16
Mathematical Theory of Vibrations of Elastic Plates
l(k*
+
u*)dv =
Up
U'J
-T->;
dv
+
1
1
)
u)
ds
If each of the two systems satisfies the stress-equations of
motion, the difference-system does also, since the equations are linear.
Thus
pu.
-TV.
•
=0
and (1.051) reduces to
K* +U* =K*(?
0
)+U*(O+ \'dt f tj u'j dS (1.053)
that is, the total energy of the difference-system is equal to the initial
energy plus the work done by the difference-tractions acting through the
difference-displacements, on the surface S, during the interval
t-to-
The argument proceeds in three steps: (1) it is shown that, if
K*+U* =0 the two systems must be identical except for a
rigid-body-displacement; (2) conditions sufficient to make K*+U*=0
are established; (3) these results are converted to conditions for the
uniqueness of a solution.
(1) If K*+U*=0, K* and U* must vanish separately, since both are
positive.
If K* vanishes, K* vanishes, since it is positive, and hence the it]
vanish since K* is proportional to the sum of the squares of the w, .
Now, U* is a homogeneous, quadratic function (of the
difference-strains) which must be positive to secure the stability of
the body (Love, 1927, p. 99). Hence if U* vanishes, U* must vanish
and, with it, the difference-strains. If the latter vanish, so must the

Elements of the Linear Theory of Elasticity 17
difference-stresses (through Hooke's Law) and the
difference-displacements, except for the displacement possible in a rigid
body.
Hence, if K*+U*=0, the two systems must be identical except,
possibly, for a rigid-body-displacement (independent of the time since
the difference-velocities vanish) and the latter can be eliminated by
requiring the initial displacements to be the same.
(2) K* +U* will vanish under conditions sufficient to make the right
hand side of (1.053) vanish. If the initial displacements of the two
systems are the same and the initial velocities are the same, then K*(?
0
)
and U*(?
0
) vanish. This leaves only the integral in (1.053) which will
vanish if one member of each of the three terms of the product
t*u*
vanishes at each point of the surface. Thus, if n, s, t are orthogonal
directions at any point of the surface, it is sufficient that T*
n
or w* and
T^ or w* and T*
t
or u* vanish at each point.
(3) Returning, now, to a single system, sufficient conditions for a unique
solution of the stress-equations of motion (subject to the limitations noted
below) are
(a) Specification of the initial displacement and velocity throughout
the body.
(b) Specification, at each and every point of the surface, of any one
of
the
eight combinations formed by choosing one member of each of the
three products
T„„u„,
T
m
u
s
,
T„,u
t
.
[Because of the use of a restricted form of the divergence theorem
in passing from (1.051) to (1.053), these conditions are subject to the

18
Mathematical Theory of Vibrations of Elastic Plates
limitations as to continuity, single-valuedness, singularities and behavior
at infinity associated with this form of the divergence theorem (Kellogg,
1929,
Chapter IV). Some of the limitations may be removed.
For example, conditions which assure single-valuedness of
displacements may be included in the uniqueness theorem by taking into
account the possibility of surfaces of displacement-discontinuity. In that
case (1.052) would have additional terms of the form f t*Au*dS
J
s'
J
'
where the integrations are over surfaces S' across which the
displacements have discontinuities Aw* . Then the condition
AH*
=J du* = 0, where the integration is around any closed curve C,
leads,
by Cesaro's and Weingarten's theorems, (Love, 1927, p. 222) to (1)
the necessity of the equations of compatibility; (2) their sufficiency in the
case of simply connected bodies and (3) the requirement of six additional
conditions for each degree of multiple connectivity. Alternatively, the
possibility Aw*^0 leads to the necessity of specifying (1) the
incompatibility tensor throughout the body; (2) at each point of each
surface of discontinuity, one of the eight combinations formed by
choosing one member of each of the three products
T
nn
Au„,
T
m
Au
s
, T
nt
Au
t
;
or, (3) both (1) and (2).
Another example of an extension of the scope of the uniqueness
theorem is given by Sternberg and Eubanks (1955) who included the
singularity corresponding to a concentrated force.]
It should be noted that (subject to the limitations mentioned) the
uniqueness conditions are sufficient, rather than necessary, so that there
may be other conditions sufficient for a unique solution. For example,
one or more of the three components of surface-traction may be a
function of the corresponding component of displacement, as in the case
of an elastic support.

Elements of the Linear Theory of Elasticity
19
It should also be noted that the uniqueness theorem applies to an
isolated body. In the case of a pair of bodies in juxtaposition, conditions
relating to the continuity of all six components
(T„„,
T
m
,
T„,,
u„,
u
s
, w,)
must be specified at each point of the interface.
1.06 Variational Equation of Motion
When the form of the strain-energy-function U is known, the
displacement-equations of motion may be deduced from Hamilton's
principle (Love, 1927, p. 166).
Let
K= [ KdV
IV
U= [udV
be,
respectively, the total kinetic and potential energies of the body and
let
8W
=
\ t,Su;dS (1.061)
3s
J J
be the work done by the surface-tractions when the displacement
undergoes a variation
SUJ
between fixed values at an initial time t
0
and a
final time t\. Then, by Hamilton's principle,
S{''{K-[))dt+ f' SWdt
=
0 (1.062)
Now,
5
t
Kdt=
£
dt
\Ap^?M
v
=£'
dtlpu^faM
= \
v
Pu
J
Su
j
\dV-^dt[pu
j
Su
j
dV
Since duj vanishes at t
0
and t\, the first term on the right vanishes.
Equation (1.062) then becomes the variational equation of motion

20 Mathematical Theory of Vibrations of Elastic Plates
^(pujSuj+SU)dV = J tjSuj dS
(1.063)
(Note that, if the variations in (1.063) are replaced by time derivatives,
the variational equation of motion is converted to (1.021), i.e., the
principle of conservation of energy.)
Again, with due regard to (1.0315),
5u=2Lss
tl
l du
du
is
::
--
J=
liT
OKUi
>
i+Uj
"
)=
Ts,
<j
du _
du,
K
dS
>J '
>j
K*
S
>JJ
Su,
and
I
dU _
ou,
dS, '
dU
•J J,
3S
U
dV
-J,"
.,_, Su:dS
=
0
S 'dS; '
Hence, the variational equation of motion becomes
I
dU
dS,
•pa j
ij
A;
Su
i
dV+ \
f
dU
\
v
7 dS
'U
S
Ui
dS
=
0
Then coefficients of the variations Suj must vanish separately.
Accordingly
r
du_~"
= piij
(1.064)
throughout the body and, on the surface,
dU
(1.065)
•j
1.07 Displacement-Equations of Motion
If the stress-strain relations (1.0312) are substituted in the
