Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates

Подождите немного. Документ загружается.

Solutions of the Three-Dimensional Equations 71

16c

2 3

p n

pn 4 pnc

— -tan-*—

q n

qn 4 ^qn

—+ -cot-

—

4 c 2c

Accordingly, if

cos——*0,

p = 2,4,6,...

sin—^0,

1,3,5,...

(2.1151)

(2.1152)

the slopes at £6=0 are zero and the curvatures are positive or negative

according as

If, however,

so that

pn 4 pnc > .

— rrt&n— 0

4 c

2 <

qn 4 tf;r > .

-2—

—cot-2—

4 c 2c <

pnc

cos

—

= 0

sin-

—= 0

_ q \ 9 = 3,5,...

"/>[/> = 2,4,6,...

(2.1153)

(2.1154)

(2.1155)

the curvatures are infinite and the slopes, from (2.1149) are

dCy, )

__/fV

•=+-

—, 9 = 3,5,...

(2.1156)

72 Mathematical Theory of Vibrations of Elastic Plates

Thus,

the behavior of the antisymmetric modes is similar to that of the

symmetric modes, but with one important exception. It will be observed

that (2.1154)—(2.1156) do not hold for q=\. This is because v is limited to

the range

-l<v<-

so that

—— <c <oo

Hence, even the smallest value ofp (i.e.,p=2) does not bring c within the

allowable range. This is to say that the frequency of the lowest,

antisymmetric, simple thickness-stretch mode (Fig.

2.031,

p=2) is always

higher than the frequency of the lowest antisymmetric, simple

thickness-shear mode (Fig. 2.032, q=l). Hence the coupled mode

corresponding to q=\ never goes through the cycle of change of sign of

curvature. This is illustrated by the dashed curves in Fig. 2.113. The

second antisymmetric mode always has the same character while

Poisson's ratio varies. The third antisymmetric mode, however, does go

through the cycle, since the frequency of the lowest, antisymmetric,

simple thickness-stretch mode is lower than the frequency of the second

antisymmetric thickness-shear mode (Fig. 2.032, q=i) if v< 1/10. In Fig.

2.113 the lowest value of Poisson's ratio for which the spectrum is

illustrated is v=0.25, so that in (a) the curve corresponding to p=2 (the

fourth antisymmetric mode) is already above that corresponding to q=3.

Its ordinate at

gb=0

is 2V3 , i.e., about 3.5. The next value above v=l/10

for which coincidence occurs is v= 17/42 (obtained from (2.1143) with

p=2,

q=5). This is slightly above v=0.40, for which Fig. 2.113(c) is

plotted. Hence the fourth and fifth antisymmetric modes are shown just

prior to their meeting point at

co/co

=5.

Solutions of the Three-Dimensional Equations 73

2.12 Three-Dimensional Coupled Dilatational and Equivoluminal

Modes in an Infinite Isotropic Plate with Free Faces

The solution given in Section 2.11 may be extended to include

phase reversals in the ;c

-direction.

In (1.077) we take, for the potentials of the dilatation and rotation,

<p =

f(x

)s'm^x

sin^x^e

=Ai(^

)sin^

cos^x

e''

' (2.121)

)cos^x

cos^x

=/J

)COS^X, sm£x

e"°'

These satisfy the equations of motion if (1.078) and (1.0710) are satisfied,

i.e., if

+h'

+£h

0 (2.122)

where

h'j+fhj^O, 7 = 1,2,3

+?+C=

(2.123)

Thus,

(2.124)

Asinax

+Bcosax

Cj sin J3x

Dj cosj3x

, j

1,2,3.

We find, for the components of displacement and for the

74 Mathematical Theory of Vibrations of Elastic Plates

components of traction on planes x

= constant,

(%f

+Ch

) cos gx^'m^x^'

=(f'-Ch

+th

)sm£x

sm£x

" (2.125)

=(£f-<!;h

-^Osin^cos^Xje"

=M(<?

C -p-

2({^-£h{)]smZ

smCx

[2<Zf'-(C

-p

-^h

+^h

]sm^

cos^x

" (2.126)

fj[2Zf'

- #A + £h

{? - p

]cos £*, sin ^e*

For the symmetric modes we take, from (2.124),

/ = 5cosa;c

- Q sin/?;x:

cos fix

(2.127)

- C

sin J3x

Then, the first of (2.122) and the boundary conditions

2=T

3=T

require

^C,-/?Z>

+^C3=0

(<f +^

-j3

)Bcosab -2CJ3C

{

cosj3b

2%j3C

cos/3b

0 (2.128)

-2#*5sina& -(£

-p

smpb +&D

swfib +&C

&in/3b

2%aB

sin a£ - ^C, sin/?6 - #?£>

sin/?6 + (£

-/?

sin^ = 0

When the determinant of (2.128) is set equal to zero we obtain

Solutions of the Three-Dimensional Equations

tan/?6_

Aaj3{?+C,

)

Similarly, for the antisymmetric modes, we obtain

tan

>ff6^

-fi

)

tmab~

4a/3(%

+£

)

(2.129)

(2.1210)

It will be observed that (2.129) and (2.1210) are the same as (2.116)

and (2.118) except that £

takes the place of £. (This was pointed out

by Rayleigh, 1889.) Hence, all the results obtained for the problem of

plane strain, treated in Section 2.11, hold for the three-dimensional case

if the wave-number, £ in Section 2.11, is replaced by ^

. In

particular, the frequency spectra, depicted in all the Figures in Section

2.11,

apply to the present case if this substitution is made in the

coordinates.

2.13 Solutions in Cylindrical Coordinates

The solutions given in Sections 2.07 and 2.11 have their

counterparts in cylindrical coordinates (Goodman, 1951). We refer the

plate to the cylindrical coordinate system r, 0, z and take the faces at z=

±6.

The vector potential (H

H2, i/3) is resolved into cylindrical

components (H

Hg,

) and we consider the axially symmetric case, in

which

and

are independent of

Then (1.077) become,

in cylindrical coordinates,

dq> dH

dr dz

=0 (2.131)

dcp

g |

dz dr r

=•

76 Mathematical Theory of Vibrations of Elastic Plates

and (1.0710) become

V> =

-r'

)

Equations (2.132) have solutions

<p =

f{z)J^r)e'

=h{z)J^r)e

where J

and J\ are Bessel functions and, as before,

?=co

Then

(2.132)

(2.133)

0 (2.134)

=-(£/ +A ViC^y'""

u,=(f'

th)J

tfr)e'»'

=AA

[(Z

-p

2$hVMr)e

°' (2.135)

oz or

Since the quantities in brackets in the expressions for T

and T„ are

the same as those in r

2 and T

in (2.068), and since a, /?, f and

are

related in the same way as before, all the conclusions regarding

frequencies of vibration, which were reached in the case of rectangular

coordinates, apply also to the case of cylindrical coordinates. Figures

2.091 and 2.092 give the frequency spectra for a plate held between

Solutions of the Three-Dimensional Equations 11

smooth, rigid faces and Figs.

2.111,

2.112 and 2.113 give the frequency

spectra for a plate with free faces.

Equivoluminal modes also exist, as may be seen by setting f=0,

<t=p

and h'(±b)=0 in (2.135). In this case T„ is proportional to J[{%r)

and hence the plate breaks up into traction-free rings bounded by

cylindrical surfaces J[(£r)=0. As before, planes z=constant are free of

traction at intervals 2bln.

Three-dimensional solutions in cylindrical coordinates, analogous to

those in Section 2.12, may be obtained by retaining H

and H

and setting

all functions proportional to

co?,n6

or sinw#.

2.14 Additional Boundaries

In Sections 2.11 and 2.12, dealing with coupled dilatational and

equivoluminal modes in isotropic plates with free faces, we saw that, for

either the symmetric or antisymmetric case, there is an infinite number of

modes of vibration for each ratio of thickness to wave-length. Each of

these modes can exist, in an infinite plate, independently of all the others.

This is the analogue of the independence of dilatational and

equivoluminal modes in a body with all its dimensions infinite. Now,

considering, for example, a single symmetric mode in a plate with free

faces,

we find that at intervals tj/^ along

(at every crest and trough)

boundary conditions

u\=T\y=T\

are satisfied. This is the analogue of

the case of smooth rigid boundaries (u

=Ti

=0 on x

=ib) treated in

Section 2.09. In that case we saw that relaxation of

the

condition w

=0 to

2=0

resulted in coupling of equivoluminal and dilatational modes. In an

analogous manner the relaxation of the boundary conditions wi=0 to

=0,

on planes Xi=constant, of a plate with free faces x

=±b, results in

the coupling of the infinity of modes of the type described in Section

2.11 or 2.12. Hence, with the exception of modes of the type treated in

78 Mathematical Theory of Vibrations of Elastic Plates

Section 2.07, the modes of vibration of a plate, with more free

boundaries than the free faces, are not expressible in closed form. This

leads to major computational difficulties because the equations which

then determine the frequencies and mode-shapes, analogous to (2.115)

and (2.116), contain an infinite number of terms. The same difficulty

occurs, of

course,

with crystal plates; and in these there are the additional

complications that, in general, the relation between wave-number and

frequency, analogous to (2.066), is determined by a cubic equation and

symmetric and antisymmetric motions are coupled. Thus, for both

isotropic and crystal plates it is convenient to have available approximate

equations which contain only a finite number of modes of the type

encountered in Sections 2.11 and 2.12. Such approximations are made, of

course, at the expense of limiting the applicability of the equations to

certain classes of modes and ranges of frequencies and wave-lengths.

Chapter 3

Infinite Power Series

Two-Dimensional

Equations

3.01 Introductory

As a preliminary to the establishment of various two-dimensional

approximations, we convert the three-dimensional equations of elasticity

infinite series

two-dimensional equations

expanding

the

displacement

an infinite series of powers of the thickness-coordinate

of the plate and integrating through the thickness. Thus,

the integral

expressions in Chapter 1, we let

and perform the indicated integrations with respect to x

between limits

(3.011) the summation is over integral values of n from zero

infinity and the displacement of order n is

function of

x\,

XT,

and

only,

i.e.,

uf =uf{x

,x-

,t)

(3.012)

Note that

superscript enclosed in parentheses

not

power, but only

indicates the order

the term

which

it is

attached. The first three

orders

of uf

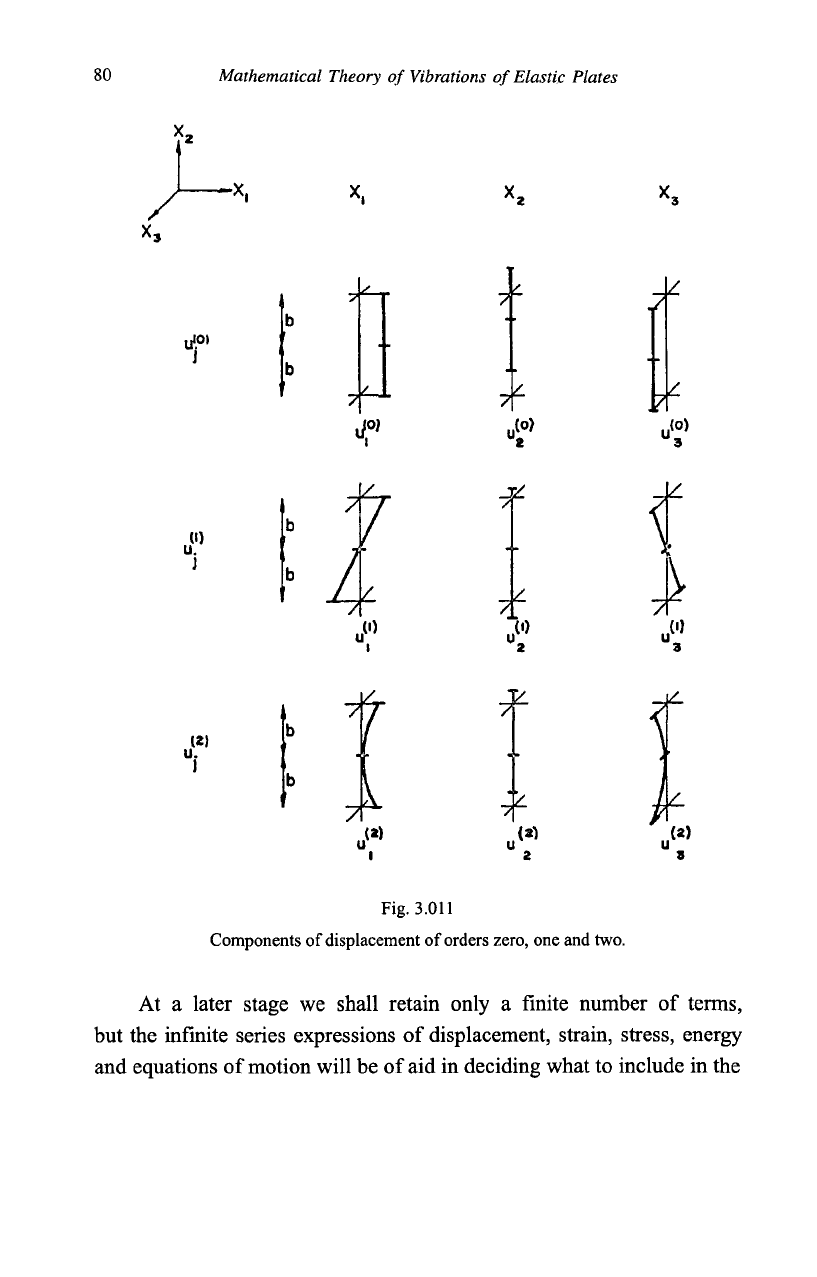
are illustrated in Fig.

3.011.

It is helpful to recognize that

a component

displacement

order

contributes

extensional

motions of the plate ify'+« is odd and to flexural motions ifj+n is even.

Mathematical Theory of Vibrations of Elastic Plates

—x.

UTOI

..C°>

(I)

12)

..«

..<«

..('I

Fig. 3.011

Components of displacement of orders zero, one and two.

At a later stage we shall retain only a finite number of terms,

but the infinite series expressions of displacement, strain, stress, energy

and equations of motion will be of aid in deciding what to include in the