Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


208 5 Discrete-Time Process Models
y(t
k
)=Cx(t
k
)+Du(t
k
) (5.87)
where
Φ(t
k+1
,t
k
)=e
AT
s
(5.88)
Γ (t
k+1
,t
k
)=
T
s
0
e
Aτ
dτ
B (5.89)
Let us denote t
k
= kT
s
. Then equations (5.86), (5.87) can be simplified as
x(k +1)=Φx(k)+Γu(k) (5.90)
y(k)=Cx(k)+Du(k) (5.91)
Matrices Φ, Γ are constant. This follows from (5.88), (5.89). Matrix D is in
majority of discrete-time systems equal to zero.
The input-output model of a system can be easily derived from state-space
description using the following procedure:
Using the relation
qx(k)=x(k + 1) (5.92)
we can write
(qI −Φ)x(k)=Γu(k) (5.93)
y(k)=C(qI − Φ)
−1
Γu(k)+Du(k) (5.94)
If (5.94) is rewritten as
y(k)=G(q)u(k) (5.95)
then
G(q)=C(qI − Φ)
−1
Γ + D (5.96)
or
G(q
−1
)=C(I −q
−1
Φ)
−1
q
−1
Γ + D (5.97)
Consider now a singlevariable case where
G(q)=
B(q)
A(q)
(5.98)
If the system order is n and polynomials B(q), A(q) are coprime then the A
polynomial has degree n. It follows from (5.98) that the polynomial A is the
characteristic polynomial of the matrix Φ and the input-output model can be
written as
5.5 State-Space Discrete-Time Models 209
y(k)=−
n
i=1
a
i
y(k − i)+
n
i=0
b
i
u(k − i) (5.99)
The coefficient b
0
is equal to zero in direct digital control, i. e. there is no
direct feed-through. The output signal is measured before the input signal
u(k) is calculated. y(k) cannot be influenced by u(k).
Of course, the same holds as with continuous-time systems: one input-
output system is equivalent to infinitely many state-space models.
Consider now a non-singular matrix T and define a new state vector as
z(k)=Tx(k) (5.100)
Further we can write
z(k +1)=TΦT
−1
z(k)+TΓu(k) (5.101)
y(k)=CT
−1
z(k)+Du(k) (5.102)
The characteristic equation of the original and transformed system is of
the form
det(λI −Φ) = 0 (5.103)
This follows from the fact that
det(λI −TΦT
−1
) = det T det(λI −Φ) det T
−1
(5.104)
= det(λI − Φ) (5.105)
If Φ has distinct eigenvalues λ
i
,i =1, 2,...,n then there exists a matrix T
such that
TΦT
−1
=
⎛
⎜
⎜
⎜
⎝
λ
1
0 ··· 0
0 λ
2
··· 0
.
.
.
.
.
.
00··· λ
n
⎞
⎟
⎟
⎟
⎠
(5.106)
Hence, the transformed system is diagonal.
If the form of the characteristic equation of the matrix Φ of a singlevariable
system is
λ
n
+ a
n−1
λ
n−1
+ ···+ a
0
= 0 (5.107)
then the system can be transformed into
z(k +1)=
⎛
⎜
⎜
⎜
⎝
01··· 0
.
.
.
.
.
.
00··· 1
−a
0
−a
1
··· −a
n−1
⎞
⎟
⎟
⎟
⎠
z(k)+
⎛
⎜
⎜
⎜
⎝
0
.
.
.
0
1
⎞
⎟
⎟
⎟
⎠
u(k) (5.108)
y(k)=
b
0
b
1
... b
n−1
z(k) (5.109)
210 5 Discrete-Time Process Models
that is called the controllable canonical form.
If the characteristic equation of the matrix Φ of a singlevariable system is
of the form (5.107) then the system can be transformed into
z(k +1)=
⎛
⎜
⎜
⎜
⎝
−a
n−1
1 ··· 0
.
.
.
.
.
.
−a
1
0 ··· 1
−a
0
0 ··· 0
⎞
⎟
⎟
⎟
⎠
z(k)+
⎛
⎜
⎜
⎜
⎝
b
n−1
.
.
.
b
1
b
0
⎞
⎟
⎟
⎟
⎠
u(k) (5.110)
y(k)=
10··· 0
z(k) (5.111)
This is called the observable canonical form.
To solve the state-space equations
x(k +1)=Φx(k)+Γu(k) (5.112)
y(k)=Cx(k) (5.113)
we can use Z-transform. Transformed equation (5.112) is of the form
z[X(z) − x(0)] = ΦX(z)+ΓU(z) (5.114)
Further, we can write
X(z)=(zI − Φ)
−1
zx(0) + (zI −Φ)
−1
ΓU(z) (5.115)
Y (z)=C(zI − Φ)
−1
zx(0) + C(zI −Φ)
−1
ΓU(z) (5.116)
where
G(z)=C(zI −Φ)
−1
Γ (5.117)
is the discrete-time transfer function matrix.
The solution x(k), y(k) can be found using the inverse Z-transform with
equations (5.115), (5.116). However, there is a much simpler way. Let us write
x(1), x(2) as
x(1) = Φx(0) + Γu(0) (5.118)
x(2) = Φx(1) + Γu(1) (5.119)
= Φ
2
x(0) + ΦΓ u(0) + Bu(1) (5.120)
Further continuation gives
x(k)=Φ
k
x(0) +
k−1
i=0
Φ
k−i−1
Γu(i),k≥ 1 (5.121)
5.6 Properties of Discrete-Time Systems 211
5.6 Properties of Discrete-Time Systems
5.6.1 Stability
A discrete-time linear system of the form
x(k +1)=Φx(k) (5.122)
is asymptotically stable in large in origin if and only if for a given symmetric
positive definite matrix Q there exists a symmetric positive definite matrix P
that satisfies solution of the Laypunov equation
Φ
T
PΦ− P = −Q (5.123)
The proof of sufficiency is very simple. Assume that a function V (x)exists
V (x)=x
T
Px (5.124)
such that
V (x) > 0; x = 0
V (0)=0
V (x) →∞ for x→∞
(5.125)
ΔV (x)=x
T
(k +1)Px(k +1)−x
T
(k)Px(k) (5.126)
ΔV (x)=x
T
(k)(Φ
T
PΦ− P )x(k) (5.127)
ΔV (x)=−x
T
(k)Qx(k) (5.128)
Thus,
ΔV (x) < 0 x = 0 (5.129)
as the matrix Q is positive definite. This concludes the proof.
An alternative way to check stability can be the method that determines
eigenvalues of matrix Φ.
If input-output models are studied, it can be stated that a singlevariable
discrete-time system is stable if and only if all roots of the system denominator
1+a
1
z
−1
+ ···+ a
n
z
−n
= 0 (5.130)
are within unit circle with radius in origin. This follows from the equation
z
i
=e
s
i
T
s
(5.131)
where z
i
,i=1, 2,...,n are roots of the characteristic equation. The condition
of negative s
i
is identical with the condition
|z
i
| < 1 (5.132)
212 5 Discrete-Time Process Models
5.6.2 Controllability
A discrete-time linear system with constant coefficients
x(k +1)=Φx(k)+Γu(k) (5.133)
y(k)=Cx(k) (5.134)
is completely controllable if and only if the controllability matrix
Q
Rd
=(
ΓΦΓΦ
2
Γ ··· Φ
n−1
Γ
) (5.135)
is of full rank n.
5.6.3 Observability
A discrete-time linear system with constant coefficients (5.133), (5.134) is
completely observable if and only if the observability matrix
Q
Pd
=
⎛
⎜
⎜
⎜
⎜
⎜
⎝
C
CΦ
CΦ
2
.
.
.
CΦ
n−1
⎞
⎟
⎟
⎟
⎟
⎟
⎠
(5.136)
is of full rank n.
5.6.4 Discrete-Time Feedback Systems – Control Performance
The stability issue explained above is important in feedback control of discrete-
time systems. Stability is the principal requirement in feedback control design
and is included within the general problem of control performance. If stability
is guaranteed, the next requirement is to remove the steady-state control error.
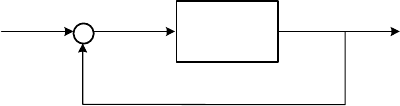
Let us explain briefly the problem. Consider the feedback discrete-time
system shown in Fig. 5.13.
_
()
1
0
−
zG
()
kw
()
ke
()
ky
Fig. 5.13. A feedback discrete-time system
The feedforward path includes a discrete-time controller R(z
−1
) and the
controlled process including D/A converter, the process, and A/D converter,

5.6 Properties of Discrete-Time Systems 213
i. e. the discretised process G(z
−1
). The open-loop transfer function is given
as
G
o
(z
−1
)=G(z
−1
)R(z
−1
) (5.137)
and can be written as
G
o
(z
−1
)=
B
o
(z
−1
)
A
o
(z
−1
)
(5.138)
where
B
o
(z
−1
)=b
o1
z
−1
+ b
o2
z
−2
+ ···+ b
om
o
z
−m
o
(5.139)
The closed-loop transfer function with the input w and output y is
G
c
(z
−1
)=
G
o
(z
−1
)
1+G
o
(z
−1
)
(5.140)
or
G
c
(z
−1
)=
B
o
(z
−1
)
A
o
(z
−1
)+B
o
(z
−1
)
(5.141)
The output in steady-state for a unit step on input can be derived by substitut-
ing for z = 1 into the closed-loop transfer function. To remove the steady-state
control error, the following has to hold in the steady-state
G
c
(1) = 1 (5.142)
From the equation
G
c
(1) =
*
m
0
i=1
b
i
A
o
(1) +
*
m
o
i=1
b
i
(5.143)
follows the condition for the zero steady-state control error
m
o
i=1
b
oi
=0,A
o
(1) = 0 (5.144)
From the requirement A
o
(1) = 0 yields that A
o
(z
−1
) has to be of the form
A
o
(z
−1
)=(1− z
−1
)
¯
A
o
(z
−1
) (5.145)
where
¯
A
o
(z
−1
)=1+a
1
z
−1
+ ···+ a
n
o
−1
z
−n
o
−1
(5.146)
From this follows that if the open-loop transfer function contains a digital
integrator, the feedback control will guarantee the zero steady-state control
error.
214 5 Discrete-Time Process Models
5.7 Examples of Discrete-Time Process Models
This section explains a general procedure how discrete-time process models
can be obtained on some concrete examples.
5.7.1 Discrete-Time Tank Model
Consider a tank filled with a liquid shown in Fig. 2.1 on page 16. Linearised
state-space model of the tank is given as
dx
dt
= ax + bu (5.147)
y = x (5.148)
where
x = h − h
s
u = q
0
− q
s
0
a = −
k
11
2F
√
h
s
,b=
1
F
t is time, h – liquid level in the tank, q
0
– inlet volumetric flow rate, F –
cross-sectional area of the tank, h
s
– steady-state level, q
s
0
– steady-state flow
rate, and k
11
is a constant.
Let us find a model of the tank that makes it possible to find transient
response of the tank in times t
k
for the input variable given as
u(k)=u(t
k
); t
k
<t≤ t
k+1
; k =0, 1, 2,... (5.149)
The solution can be found as follows. Comparing equations (5.147) and (5.148)
with the general state-space model gives
A = a, B = b, C =1, D = 0 (5.150)
The discrete-time state matrix Φ(t)forA = a is
Φ(t)=L
−1
(s −a)
−1
= L
−1
1
s −a
=e
at
(5.151)
Hence,
Φ(T
s
)=e
aT
s
(5.152)
From (5.89) follows
Γ =
T
s
0
e
aτ
dτ
b =
b
a
e
aT
s
− 1
(5.153)
Finally, equation (5.90) gives
x(k +1)=e
aT
s
x(k)+
b
a
(e
aT
s
− 1)u(k) (5.154)
The process output y = x can be found from this equation in sampling times
for u(k).

5.7 Examples of Discrete-Time Process Models 215
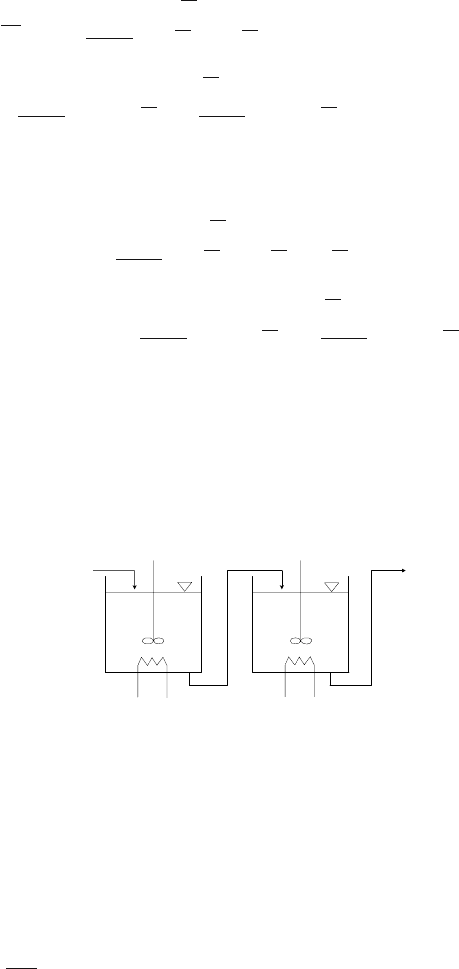
5.7.2 Discrete-Time Model of Two Tanks in Series
Consider two tanks in series shown in Fig 3.10 on page 86. The behaviour of
the second tank is influenced by that of the first tank.
Let us define new variables
x
1
= h
1
− h
s
1
,x
2
= h
2
− h
s
2
y = x
2
,u= q
0
− q
s
0
T
1
=
2F
1
h
s
1
k
11
,T
2
=
2F
2
h
s
2
k
22
,Z=
2
h
s
2
k
22
The symbol definitions are evident from Fig. 3.10 and from Section 5.7.1. The
superscript (.)
s
denotes the variable in steady-state.
The linearised state-space model of the tanks is characterised by matrices
A =
⎛
⎜
⎝
−
1
T
1
0
Z
T
2
−
1
T
2
⎞
⎟
⎠
, B =
⎛
⎝
1
T
1
0
⎞
⎠
, C =
01
(5.155)
The corresponding input-output model of the process is given by the dif-
ferential equation
T
1
T
2
d
2
y
dt
2
+(T
1
+ T
2
)
dy
dt
+ y = Zu (5.156)
The state transition matrix is given as
Φ(t)=L
−1
$
s 0
0 s
−
01
−a
0
−a
1
−1
%
(5.157)
= L
−1
$
s −1
a
0
s + a
−1
%
(5.158)
= L
−1
⎧
⎪
⎨
⎪
⎩
s + a
1
s
2
+ a
1
s + a
0
1
s
2
+ a
1
s + a
0
−a
0
s
2
+ a
1
s + a
0
s
s
2
+ a
1
s + a
0
⎫
⎪
⎬
⎪
⎭
(5.159)
=
T
1
T
1
−T
2
e
−
t
T
1
+
T
2
T
2
−T
1
e
−
t
T
2
T
1
T
2
T
1
−T
2
e
−
t
T
1
+
T
1
T
2
T
2
−T
1
e
−
t
T
2
1
T
2
−T
1
e
−
t
T
1
+
1
T
1
−T
2
e
−
t
T
2
T
2
T
2
−T
1
e
−
t
T
1
+
T
1
T
1
−T
2
e
−
t
T
2
(5.160)
Φ(T
s
)=
⎛
⎝
e
−
T
s
T
1
0
ZT
1
T
2
−T
1
e
−
T
s
T
2
− e
−
T
s
T
1
e
−
T
s
T
2
⎞
⎠
(5.161)
From (5.89) follows
216 5 Discrete-Time Process Models
Γ =
1
T
1
T
s
0
e
−
τ
T
1
ZT
1
T
2
−T
1
e
−
τ
T
2
− e
−
τ
T
1
dτ (5.162)
=
⎛
⎝
1 −e
−
T
s
T
1
ZT
2
T
2
−T
1
1 −e
−
T
s
T
2
+
ZT
1
T
1
−T
2
1 −e
−
T
s
T
1
⎞
⎠
(5.163)
Therefore, the discrete-time state-space representation can be given as (see
also (5.90))
x
1
(k +1)
x
2
(k +1)
=
⎛
⎝
e
−
T
s
T
1
0
ZT
1
T
2
−T
1
e
−
T
s
T
2
− e
−
T
s
T
1
e
−
T
s
T
2
⎞
⎠
x
1
(k)
x
2
(k)
+
⎛
⎝
1 −e
−
T
s
T
1
ZT
2
T
2
−T
1
1 −e
−
T
s
T
2
+
ZT
1
T
1
−T
2
1 −e
−
T
s
T
1
⎞
⎠
u(k)(5.164)
This equation specifies y = x
2
in the sampling times if the input variable u(k)
is a piece-wise constant.
5.7.3 Steady-State Discrete-Time Model of Heat Exchangers
in Series
1
ϑ
0
ϑ
ω
1
ω
2
1
ϑ
2
ϑ
V
2
V
1
2
ϑ
...
Fig. 5.14. Series of heat exchangers
Consider a series of n heat exchangers where liquid is heated (Fig. 5.14).
We assume that heat flows from heat sources into liquid are independent from
liquid temperature. Further an ideal liquid mixing and zero heat losses are
assumed. We neglect accumulation ability of exchangers walls. Hold-ups of
exchangers, as well as flow rates, liquid specific heat capacity are constant.
Under these assumptions for the first heat exchanger holds
V
1
ρc
p
dϑ
1
dt
= qρc
p
ϑ
0
− qρc
p
ϑ
1
+ ω
1
(5.165)
where t is time,
ϑ
1
– outlet temperature of the heat exchanger,
ϑ
0
– inlet temperature,

5.8 References 217
ω
1
– heat input,
V
1
– volume of liquid in the exchanger,
ρ – liquid density,
c
p
– liquid specific heat capacity.
The condition for steady-state is dϑ
1
/dt = 0. This yields for the first heat
exchanger
qρc
p
(ϑ
0
− ϑ
1
)+ω
1
= 0 (5.166)
Let us define state variables
x
m
= ϑ
m
,m=1, 2,...,n (5.167)
and input variables
u
m
= −
1
qρc
p
ω
m
,m=1,...,n (5.168)
The first exchanger is in the steady-state given as
x
1
= x
0
+ u
1
(5.169)
The m + 1th exchanger is in the steady-state given as
x
m+1
= x
m
+ u
m+1
(5.170)
All heat exchangers can thus in steady-state be written as
x
1
= x
0
+ u
1
(5.171)
x
2
= x
0
+ u
1
+ u
2
(5.172)
.
.
.
x
m
= x
0
+
m
i=1
u
i
(5.173)
.
.
.
x
n
= x
0
+
n
i=1
u
i
(5.174)
Variable m in (5.171)–(5.174) denotes one of the heat exchangers. This points
out possibilities to generalise theory of discrete-time systems.
5.8 References
The problem of computer control and discrete-time systems has been fre-
quently dealt with. We give here only some works – the ones that fundamen-
tally contributed to further advance in the field.
