Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.

198 5 Discrete-Time Process Models
f(t) F (s) F (z)
δ(t) 1 1
1(t)
1
s
z
z − 1
1(t) − 1(t − T
s
)
1 − e
−T
s
s
s
1
t1(t)
1
s
2
T
s
z
(z − 1)
2
e
−at
1(t)
1
s + a
z
z − e
−aT
s
te
−at
1(t)
1
(s + a)
2
T
s
ze
−aT
s
(z − e
−aT
s
)
2
e
−at
sin(ωt)1(t)
ω
(s + a)
2
+ ω
2
ze
−aT
s
sin(ωT
s
)
z
2
− 2ze
−aT
s
cos(ωT
s
)+e
−2aT
s
e
−at
cos(ωt)1(t)
s + a
(s + a)
2
+ ω
2
z
2
− ze
−aT
s
cos(ωT
s
)
z
2
− 2ze
−aT
s
cos(ωT
s
)+e
−2aT
s
1
ab
+
1
a(a − b)
e
−at
1
s(s + a)(s + b)
z
ab(z − 1)
+
z
a(a − b)(z −e
−aT
s
)
+
1
b(b − a)
e
−bt
1(t)
+
z
b(b − a)(z −e
−bT
s
)
c
ab
+
c − a
a(a − b)
e
−at
s + c
s(s + a)(s + b)
cz
ab(z − 1)
+
z(c − a)
a(a − b)(z −e
−aT
s
)
+
c − b
b(b − a)
e
−bt
1(t)
+
z(c − b)
b(b − a)(z −e
−bT
s
)
Table 5.1. Laplace and Z-transforms of some common functions
Polynomial Division
The Z-transform definition gives
F (z)=
∞
k=0
f(k)z
−k
(5.40)
From this follows that
F (z)=f (0) + f(1)z
−1
+ f(2)z
−2
+ ··· (5.41)
To simplify expressions, we have replaced f(kT
s
)byf(k). If we can somehow
obtain the function F (z)as
F (z)=c
o
+ c
1
z
−1
+ c
2
z
−2
+ ··· (5.42)
then by equating (5.41) and (5.42) follows

5.2 Z – Transform 199
c
0
= f(0),c
1
= f(1),c
2
= f(2), ··· (5.43)
If rational functions are considered, equation (5.42) can be found simply by
polynomial division.
Partial Fraction Expansion
The inverse Z-transform using partial fraction expansion is similar to the
inverse Laplace transform.
A function F (z) can be expressed as a ratio of two polynomials of the form
F (z)=
M(z
−1
)
N(z
−1
)
(5.44)
where
M(z
−1
)=m
0
+ m
1
z
−1
+ ···+ m
m
z
−m
(5.45)
N(z
−1
)=1+n
1
z
−1
+ ···+ n
n
z
−n
(5.46)
Let us assume that m<nand that the polynomial N (z)hasn unequal real
roots
N(z
−1
)=(1− z
1
z
−1
)(1 −z
2
z
−1
) ···(1 −z
n
z
−1
) (5.47)
Partial fraction expansion gives
F (z)=
K
1
1 −z
1
z
−1
+
K
2
1 −z
2
z
−1
+ ···+
K
n
1 −z
n
z
−1
(5.48)
The corresponding time domain function f(kT
s
)is
f(k)=Z
−1
K
1
1 −z
1
z
−1
+ Z
−1
K
2
1 −z
2
z
−1
+ ···+ Z
−1
K
n
1 −z
n
z
−1
(5.49)
or
f(kT
s
)=K
1
z
k
1
+ K
2
z
k
2
+ ···+ K
n
z
k
n
(5.50)
If the denominator of F (z) has complex conjugate roots, partial fraction
expansion gives fractions with complex denominators. This can be handled
similarly as in case of the inverse Laplace transform.
Example 5.1: Inverse Z-transform using partial fraction expansion
Consider a function F (z)oftheform
F (z)=
z
z
2
− 1.4z +0.4
or

200 5 Discrete-Time Process Models
F (z)=
z
−1
1 −1.4z
−1
+0.4z
−2
The denominator polynomial has roots z
−1
1
=1andz
−1
2
=2.5. F (z)can
be written using partial fractions as
F (z)=
z
−1
(1 −z
−1
)(1 −0.4z
−1
)
=
K
1
1 −z
−1
+
K
2
1 −0.4z
−1
Multiplying F (z)by1− z
−1
and substituting for z
−1
= 1 yields
K
1
=
5
3
Multiplying F (z)by1− 0.4z
−1
and substituting for z
−1
=2.5 yields
K
2
= −
5
3
Table 5.1 gives a corresponding time domain function (step function) for
expression (5/3)(1 −z
−1
)
(5/3) 1(kT
s
)
The term (−5/3)(1 −0.4z
−1
) is in time domain
−
5
3
e
−akT
s
where e
−aT
s
=0.4=2/5 and thus
aT
s
= −ln 0.4=0.916
Therefore, the time domain function corresponding to F (z) is given as
f(kT
s)
=
5
3
1 −e
−0.916k
=
5
3
1 −
2
5
k
,k=0, 1, 2,...
Analytical form of the corresponding continuous-time exponential func-
tion can be found only if the sampling period T
s
is known.
5.3 Discrete-Time Transfer Functions
Let us calculate a transient response of a combined discrete-time and continuous-
time system shown in Fig. 5.9. The signal
u
∗
(τ)=
∞
k=0
u(kT
s
)δ(τ − kT
s
) (5.51)
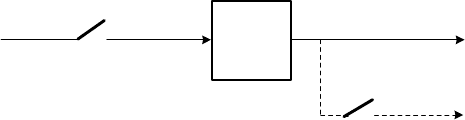
5.3 Discrete-Time Transfer Functions 201
()
tu
()
sU
()
sG
()
tu
∗
()
sU
*
s
T
()
ty
∗
()
sY
∗
s
T
()
ty
()
sY
Fig. 5.9. Sample-and-hold device in series with a continuous-time system
is on the input of the continuous-time system with transfer function G(s).
The system response y(t) is given by the convolution integral
y(t)=
t
0
g(t −τ )
∞
k=0
u(kT
s
)δ(τ − kT
s
)dτ (5.52)
where τ is time and g(t)=L
−1
{G(s)}. Equation (5.52) for 0 ≤ τ ≤ t can be
written as
y(t)=
∞
k=0
g(t −kT
s
)u(kT
s
) (5.53)
Let us further assume only information about y(t) in sampling instants. There-
fore, the output of the process enters a fictitious sampler that is ideally syn-
chronised with the input sampler u
∗
(t). The output sampler gives the signal
y
∗
(t) and its values are the same as the values of y(t) in the sampling instants.
For t = jT
s
holds
y(jT
s
)=
∞
k=0
g(jT
s
− kT
s
)u(kT
s
) (5.54)
Applying the Z-transform yields
Y (z)=
∞
j=0
∞
k=0
g(jT
s
− kT
s
)u(kT
s
)z
−j
(5.55)
If j − k = i, then
Y (z)=
∞
i=−k
∞
k=0
g(iT
s
)u(kT
s
)z
−(i+k)
(5.56)
g(t) is the response of the continuous-time system to the unit impulse with
zero initial conditions, hence g(iT
s
)=0,i<0. The first summation term on
the right-hand side of (5.56) is thus simplified (k falls out) and summations
can be written separately:
202 5 Discrete-Time Process Models
Y (z)=
∞
i=0
g(iT
s
)z
−i
∞
k=0
u(kT
s
)z
−k
(5.57)
The Z-transform definition given by (5.24) gives
Y (z)=G(z)U(z) (5.58)
G(z)=Z{g(t)} =
∞
i=0
g(iT
s
)z
−i
(5.59)
The function G(z) is referred to as discrete-time transfer function of the sys-
tem with continuous-time transfer function G(s).
The term
U(z)=Z{u(t)} =
∞
k=0
u(kT
s
)z
−k
(5.60)
is Z-transform of the input signal u(t).
In the rest of the book will G(z) be simply referred to as transfer function.
Equation (5.58) seems to be the same as its continuous-time counterpart
using the Laplace transform. However, Y (z) only indicates information about
y(t) in sampling times. G(z) does not relate input and output signals at times
between sampling times. A possible way to have information between sampling
times is to employ a generalised Z-transform.
()
tu
()
sU
()
sG
()
tu
∗
()
sU
*
s
T
()
ty
∗
()
sY
∗
s
T
()
ty
()
sY
s
e
sT
s
−
−1
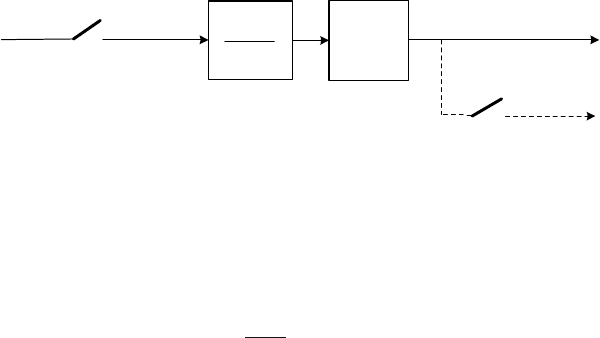
Fig. 5.10. Sampler and zero-order hold in series with a continuous-time system
G(s)
When the sample-and-hold device in Fig 5.9 is assumed to be zero-order
hold (Fig. 5.10) then the relation between G(s)andG(z)is
G(z)=(1− z
−1
)Z
L
−1
G(s)
s
(5.61)
Example 5.2: Z-transform of a continuous-time first order system with zero-
order hold
Let us find discrete-time transfer function of a continuous-time system
given by
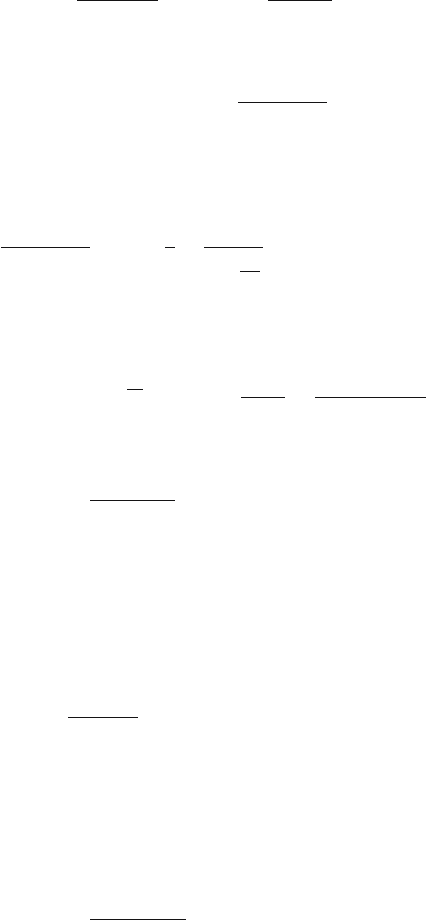
5.3 Discrete-Time Transfer Functions 203
G(s)=G
1
(s)G
2
(s)
where
G
1
(s)=
1 −e
−sT
s
s
,G
2
(s)=
Z
1
T
1
s +1
Applying equation (5.61) gives
G(z)=(1− z
−1
)Z
L
−1
Z
1
s(T
1
s +1)
In this case Z-transform of the term Z
1
/ (s(T
1
s + 1)) is needed. Partial
fraction expansion gives
Z
1
s(T
1
s +1)
= Z
1
⎛
⎜
⎝
1
s
−
1
s +
1
T
1
⎞
⎟
⎠
The right-hand side term corresponds to continuous-time function Z
1
(1 −
e
−t/T
1
). Table 5.1 gives
Z
Z
1
1 −e
−
t
T
1
= Z
1
z
z −1
−
z
z − e
−(T
s
/T
1
)
Finally
G(z
−1
)=
b
1
z
−1
1+a
1
z
−1
where b
1
= Z
1
(1 −e
−(T
s
/T
1
)
), a
1
=e
−(T
s
/T
1
)
.
Example 5.3: Z-transform of a continuous-time time-delayed first order sys-
tem with zero-order hold
Let us find discrete-time transfer function of a continuous-time system
given by
G(s)=
Z
1
e
−T
d
s
T
1
s +1
where T
d
is a time delay. Let us suppose that
T
d
= dT
s
is an integer multiple of the sampling period. The discrete-time transfer
function is of the form
G(z
−1
)=
z
−d
(b
1
z
−1
)
1+a
1
z
−1
where b
1
, a
1
are the same as in the previous example.

204 5 Discrete-Time Process Models
Example 5.4: Z-transform of a continuous-time second order system with
zero-order hold
Let us find discrete-time transfer function of a continuous-time system
given by
G(s)=
Z
2
(T
1
s + 1)(T
2
s +1)
,T
1
= T
2
The discrete-time transfer function is of the form
G(z)=(1− z
−1
)Z
L
−1
Z
2
s(T
1
s + 1)(T
2
s +1)
Partial fraction expansion and Table 5.1 give
G(z)=
Z
2
T
1
T
2
(z − 1)
z
T
1
T
2
z
z − 1
+
zT
2
1
T
2
(T
2
− T
1
)(z −e
−(T
s
/T
1
)
)
+
zT
1
T
2
2
(T
1
− T
2
)(z −e
−(T
s
/T
2
)
)
After some simplifications we find the final form
G(z
−1
)=
b
1
z
−1
+ b
2
z
−2
1+a
1
z
−1
+ a
2
z
−2
where
b
1
= Z
2
-
−
e
−
T
s
T
1
+e
−
T
s
T
2
−
T
1
(1 + e
−
T
s
T
2
)
T
2
− T
1
+
T
2
(1 + e
−
T
s
T
1
)
T
2
− T
1
.
b
2
= Z
2
-
e
−
T
s
T
1
e
−
T
s
T
2
+
T
1
e
−
T
s
T
2
T
2
− T
1
−
T
2
e
−
T
s
T
1
T
2
− T
1
.
a
1
= −
e
−
T
s
T
1
+e
−
T
s
T
2
a
2
=e
−
T
s
T
1
e
−
T
s
T
2
5.4 Input-Output Discrete-Time Models – Difference
Equations
A general discrete-time linear model can be written in time domain as
y(k)=−
n
i=1
a
i
y(k − i)+
m
i=1
b
i
u(k − d − i) (5.62)
Let us now define a shift operator q
−1
as

5.4 Input-Output Discrete-Time Models – Difference Equations 205
q
−1
y(k)=y(k − 1) (5.63)
Equation (5.62) can then be rewritten as
y(k)=−
n
i=1
a
i
q
−i
y(k)+
m
i=1
b
i
q
−(d+i)
u(k) (5.64)
or
A(q
−1
)y(k)=q
−d
B(q
−1
)u(k) (5.65)
where
A(q
−1
)=1+a
1
q
−1
+ a
2
q
−2
+ ···+ a
n
q
−n
(5.66)
B(q
−1
)=b
1
q
−1
+ b
2
q
−2
+ ···+ b
m
q
−m
(5.67)
Equation (5.65) can also be written as
y(k)
u(k)
=
q
−d
B(q
−1
)
A(q
−1
)
(5.68)
Hence, we can define a function
G(q
−1
)=
q
−d
B(q
−1
)
A(q
−1
)
(5.69)
that formally coincides with the discrete-time transfer function G(z)ifwe
replace q
−1
for z
−1
G(z
−1
)=
z
−d
B(z
−1
)
A(z
−1
)
(5.70)
5.4.1 Direct Digital Control
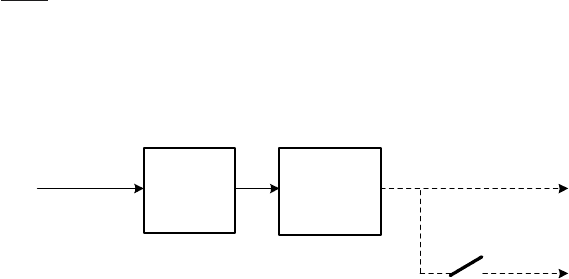
Direct digital control can be represented by the block scheme shown in
Fig. 5.11.
(
)
1−
zR
(
)
1−
zG
()
kw
()
ke
()
ku
()
ky
_
Fig. 5.11. Direct digital control
Difference equation used for determination of the manipulated variable
(discrete-time control law) is given as

206 5 Discrete-Time Process Models
u(k)=−
r
i=1
p
i
u(k − i)+
r
i=0
q
i
e(k − i) (5.71)
where p
i
and q
i
are constants. Computer that implements the control law
remembers the past values of control errors and of manipulated variables. It
then calculates the control law from (5.71) in sampling times. Constants p
i
(i =
1, 2,...,r)andq
i
(i =0, 1,...,r) are calculated in control design procedure.
If the shift operator q
−1
is used then (5.71) can be given as
u(k)=−
r
i=1
p
i
q
−i
u(k)+
r
i=0
q
i
q
−i
e(k) (5.72)
or
P (q
−1
)u(k)=Q(q
−1
)e(k) (5.73)
where
P (q
−1
)=1+p
1
q
−1
+ p
2
q
−2
+ ···+ p
r
q
−r
(5.74)
Q(q
−1
)=q
0
+ q
1
q
−1
+ q
2
q
−2
+ ···+ q
r
q
−r
(5.75)
If we write equation (5.73) as
u(k)
e(k)
=
Q(q
−1
)
P (q
−1
)
(5.76)
we can see that we get a function
R(q
−1
)=
Q(q
−1
)
P (q
−1
)
(5.77)
This is formally equivalent to the discrete-time transfer function if q
−1
is
replaced by z
−1
R(z
−1
)=
Q(z
−1
)
P (z
−1
)
(5.78)
Equations (5.70), (5.78) define transfer functions.
Discrete-time transfer function without time delay with input u and output
y can in general be written as
G(z)=
b
0
z
m
+ b
1
z
m−1
+ ···+ b
m
z
n
+ a
1
z
n−1
+ ···+ a
n
(5.79)
The corresponding difference equation is
y(k + n)+a
1
y(k + n −1) + ···+ a
n
y(k)
= b
0
u(k + m)+b
1
u(k + m − 1) + ···+ b
m
u(k) (5.80)
5.5 State-Space Discrete-Time Models 207
From this follows that a system with a transfer function is only realisable if
the degree of the numerator polynomial is smaller than or equal to the degree
of the denominator polynomial
n ≥ m (5.81)
System poles are roots of the denominator of G(z), i. e. roots of the char-
acteristic polynomial.
System zeros are poles of the inverse system.
5.5 State-Space Discrete-Time Models
Consider a continuous-time system described by state-space equations
dx(t)
dt
= Ax(t)+Bu(t) (5.82)
y(t)=C(t)+Du(t) (5.83)
System order of this system is n, the system has m inputs and r outputs.
A, B, C, D are constant matrices of appropriate dimensions.
Zero-order
hold
Continuous-
time system
()
tu
∗
()
sU
∗
()
ty
∗
()
sY
∗
s
T
()
ty
()
sY
Fig. 5.12. Zero-order hold in series with a continuous-time system
If the continuous-time system given by (5.82), (5.83) is in series with the
zero-order hold (Fig. 5.12) then
x(t
k+1
)=e
A(t
k+1
−t
k
)
x(t
k
)+
t
k+1
t
k
e
A(t
k+1
−τ)
dτ
Bu(t
k
) (5.84)
The zero-order hold ensures that the input signal u(t), t
k
≤ t<t
k+1
, k =
...,−1, 0, 1,..., is piece-wise constant. If the sampling time is constant
T
s
= t
k+1
− t
k
(5.85)
then the sampled data system equations are given as
x(t
k+1
)=Φ(t
k+1
,t
k
)x(t
k
)+Γ (t
k+1
,t
k
)u(t
k
) (5.86)
