Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


188 4 Dynamical Behaviour of Processes
1. the Nyquist diagram,
2. the Bode diagram.
Exercise 4.5:
Consider a system with the transfer function given as
T (s)=
G(s)R(s)
1+G(s)R(s)
where G(s) is in the first exercise and R(s) is in the third exercise. Find:
1. response of the system to the unit step,
2. the Bode diagram.
Exercise 4.6:
Consider a system with the transfer function given as
S(s)=
1
1+G(s)R(s)
where G(s) is in the first exercise and R(s) is in the third exercise. Find its
Bode diagram.
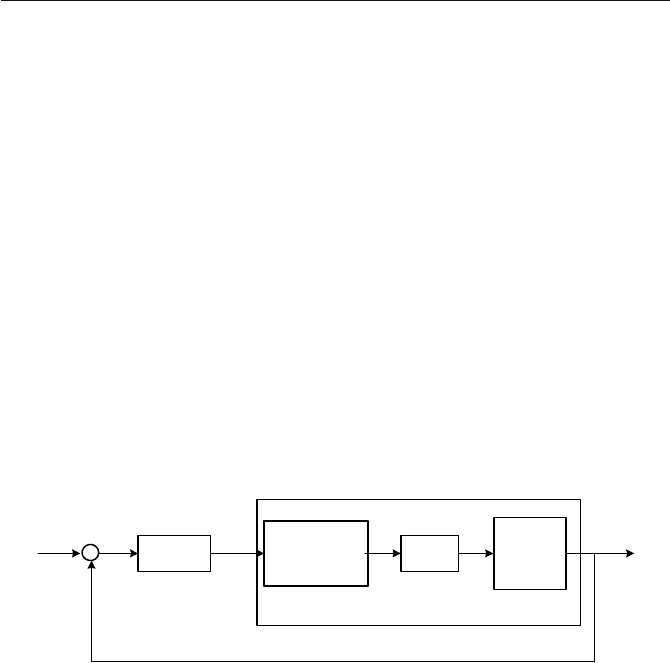
5
Discrete-Time Process Models
The aim of this chapter is to explain the reason why discrete-time process
models are used. It has a close relation to computer control of processes.
The chapter demonstrates how discrete-time processes and discrete transfer
functions are obtained. Basic properties of discrete-time systems are examined.
5.1 Computer Controlled and Sampled Data Systems
()
s
kTw
Computer
Discretised process
D/A converter
with S/H
()
tu
Process
()
ty
AD
converter
with S/H
()
s
kTe
()
s
kTu
()
s
kTy
_
Fig. 5.1. A digital control system controlling a continuous-time process
Computer controlled process control indicates that the control law is cal-
culated by computer. A feedback scheme of such a control is shown in Fig. 5.1.
This is a simplified scheme of direct digital control. The scheme in Fig. 5.1
contains four basic blocks: computer, digital-to-analog (D/A) converter, con-
trolled process, and analog-to-digital (A/D) converter. Both converters con-
tain sample-and-hold (S/H) device (or simply sampler) that holds each sample
constant until a new information arrives. The control error e(kT
s
) is given as
the difference between the setpoint signal w(kT
s
) and controlled process out-
put y(kT
s
) in digital form in sampling times specified by the sampling period
T
s
. The computer interprets the signal e(kT
s
) as a sequence of numbers and
given the control law, it generates a new sequence of control signals u(kT
s
).
190 5 Discrete-Time Process Models
The discretised process represents a system with input being the sequence
[u(kT
s
)] and output being the sequence [y(kT
s
)]. This system is characterised
by a discrete-time model that defines relations between sequences [u(kT
s
)]
and [y(kT
s
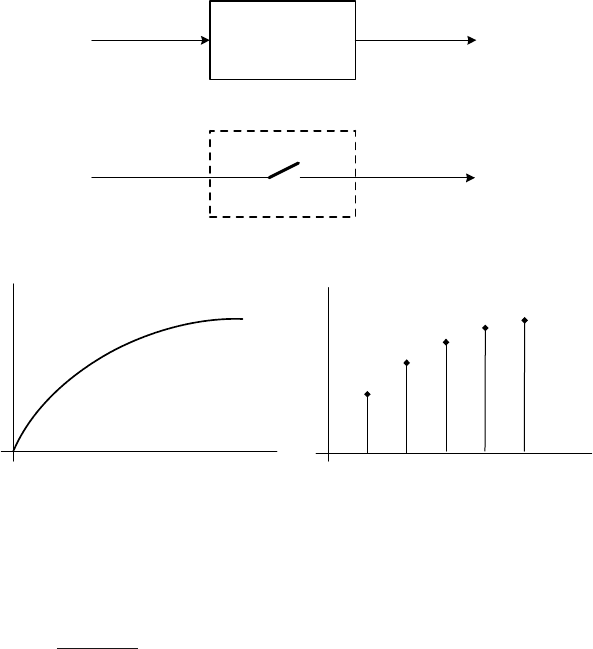
)]. A/D converter implements transformation of a continuous-time
signal to a sequence of numbers (Fig. 5.2). D/A converter with a sampler
implements transformation of a digital signal to a continuous-time signal that
is constant within one sampling period (Fig. 5.3). A/D and D/A converters
operate synchronously.
y
0 t
AD
converter
()
ty
()
s
kTy
Sampler
continuous-time
signal
discrete-time
signal
t
0
s
T
s
T2
s
T3
s
T4
s
T5
∗
y
Fig. 5.2. Transformation of a continuous-time to a discrete-time signal
A possible realisation of a sampler is zero-order hold with the transfer
function of the form
G(s)=
1 −e
−T
s
s
s
(5.1)
When processes are controlled digitally, it is important to choose a suitable
sampling period T
s
that will capture the process dynamics correctly. There
are two contradictory requirements on its choice. When computational load
is considered, the sampling period as large as possible should be chosen. On
the other hand, large sampling times imply loss of information.
In any case, the sampling period cannot be larger than some critical value
at which important information about the continuous-time signal can be lost.
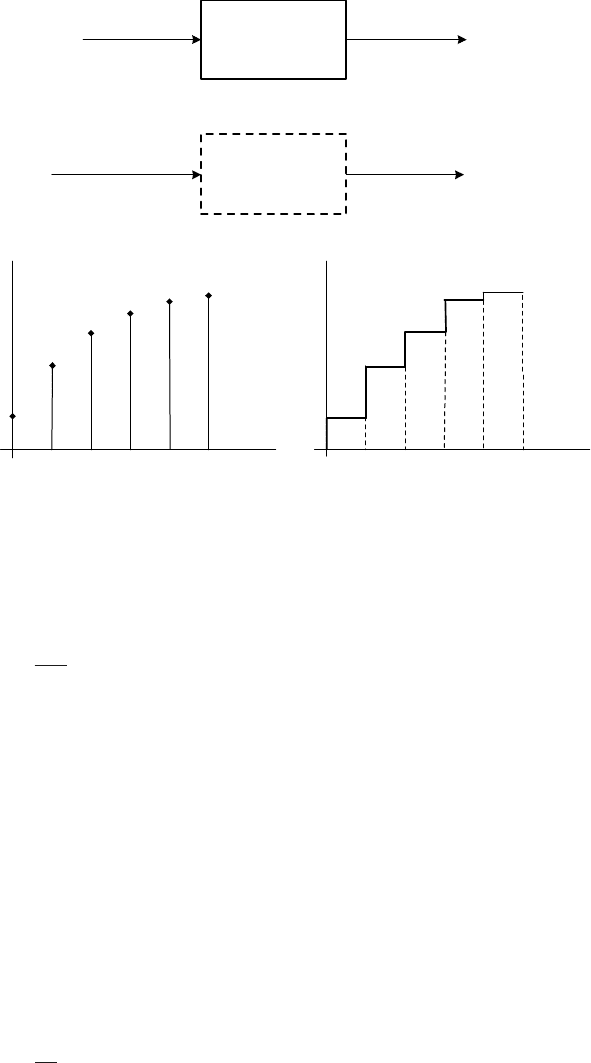
5.1 Computer Controlled and Sampled Data Systems 191
D/A converter
with S/H
()
tu
()
s
kTu
Zero-order hold
continuous-time
signal
discrete-time
signal
t
0
u
u
t
s
T
s
T2
s
T3
s
T4
s
T5
s
T
s
T2
s
T3
s
T4
s
T5
0
Fig. 5.3. Continuous-time signal step reconstruction from its discrete-time coun-
terpart
If a continuous-time sine signal is considered, loss of information occurs
when the following inequality does not hold
T
s
<
T
sin
2
(5.2)
where T
sin
is the oscillation period of the sine signal. This can be seen in
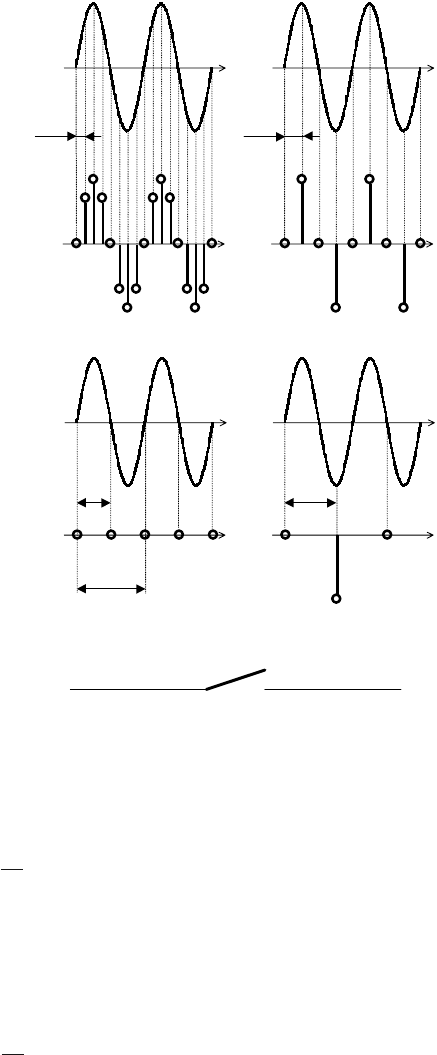
Fig. 5.4.
If (5.2) is not valid, the phenomenon occurring with the sine signal can
also occur with other sampled continuous-time signals.
If this phenomenon is studied using magnitude frequency spectra then it
will be shown by aliasing of individual spectral densities.
Let us now investigate properties of an ideal sampler shown in Fig. 5.5. Its
output variable y
∗
can be represented as a sequence of modulated δ functions.
A periodical sequence of δ functions can be represented as
δ
∗
(t)=
∞
k=−∞
δ(t −kT
s
) (5.3)
Let us define the sampling frequency
ω
s
=
2π
T
s
(5.4)
192 5 Discrete-Time Process Models
T
s1
T
s2
t
t
t
t
T
s3
T
s4
t
t
t
t
T
sin
Fig. 5.4. A possible loss of information caused by sampling
()
ty
()
ty
∗
s
T
Fig. 5.5. An ideal sampler
Then this sequence can be expressed using the exponential form of the Fourier
series
δ
∗
(t)=
ω
s
2π
∞
n=−∞
e
−jnω
s
t
(5.5)
The output variable of the ideal sampler can then be written as
y
∗
(t)=y(t)δ
∗
(t) y(t) ≡ 0,t <0 (5.6)
Substituting δ
∗
(t) from (5.5) into equation (5.6) yields
y
∗
(t)=
ω
s
2π
y(t)
∞
n=−∞
e
−jnω
s
t
(5.7)

5.1 Computer Controlled and Sampled Data Systems 193
or
y
∗
(t)=
1
T
s
y(t)
∞
n=−∞
e
−jnω
s
t
(5.8)
The Fourier transform of this function if y(0) = 0 is given as
∞
0
y
∗
(t)e
−jωt
dt =
1
T
s
∞
0
y(t)e
−jωt
∞
n=−∞
e
−jnω
s
t
dt (5.9)
Next, the following holds
Y
∗
(jω)=
1
T
s
∞
n=−∞
∞
0
e
−j(ω+nω
s
)t
y (t)dt (5.10)
Y
∗
(jω)=
1
T
s
∞
n=−∞
Y [j(ω + nω
s
)] (5.11)
as for the Fourier integral holds
∞
0
y(t)e
−j(ω+nω
s
)t
dt = Y [j(ω + nω
s
)] (5.12)
Substituting s for jω in equation (5.11) gives
Y
∗
(s)=
1
T
s
∞
n=−∞
Y (s +jnω
s
) (5.13)
It is clear from (5.11) that the transform Y (jω) is only nω
s
shifted form of
the function y(t). If the spectral density function of the variable y(t)is|Y (jω)|
(see Fig. 5.7) then the spectral density of the sampled signal y
∗
(t) is given as
|Y
∗
(jω)| =
1
T
s
∞
n=−∞
Y [j(ω + nω
s
)]
(5.14)
-ω
C
ω
C
ω
|Y(jω)|
Fig. 5.6. Spectral density of a signal y(t)
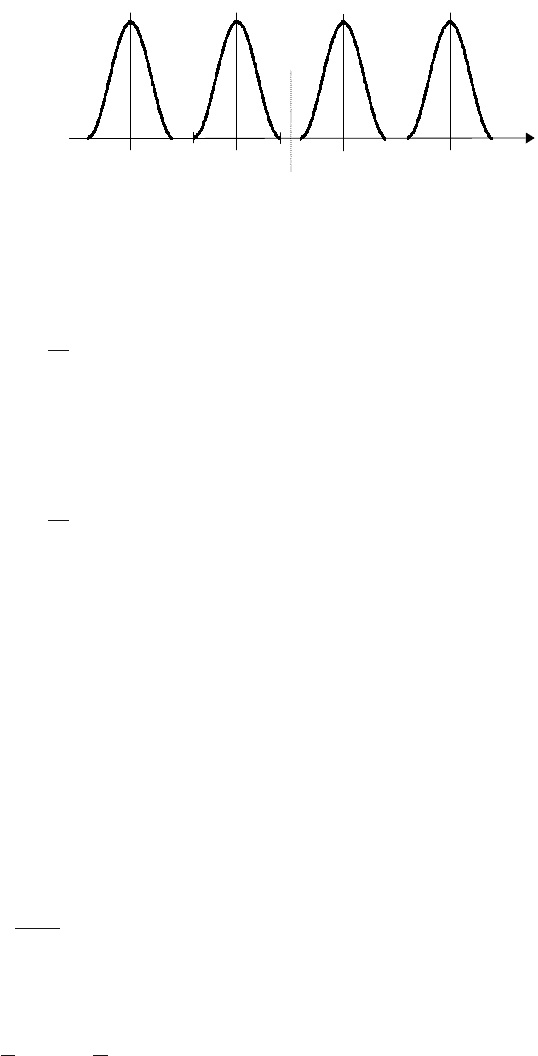
194 5 Discrete-Time Process Models
-
ω
S
ω
S
2
ω
S
-
ω
C
ω
C
0
|Y*(j
ω
)|
ω
ω
S
/2
Fig. 5.7. Spectral density of a sampled signal y
∗
(t)
Two cases can occur. In the first one the frequency ω
c
is smaller than or
equal to half of the sampling period, hence
ω
c
≤
ω
s
2
(5.15)
In this case the spectral density of |Y
∗
(jω)| is composed of spectra of
|Y (jω)| shifted to the right of nω
s
and that are non-overlapping.
The second case occurs if the frequency ω
c
is larger than half of the sam-
pling period
ω
c
>
ω
s
2
Here the spectral density of |Y
∗
(jω)| consists of spectra |Y (jω)| shifted to the
right of nω
s
and overlapping. Hence, the spectral density of the signal |Y
∗
(jω)|
is distorted.
The previous analysis has shown that it is imperative for non-overlapping
spectral densities that the sampling period obeys the relation
ω
s
≥ 2ω
c
(5.16)
Overlapping of the spectra can be removed when a suitable anti-aliasing filter
is used for the original continuous-time signal before sampling.
The sampling period choice is rather a problem of experience than some
exact procedure. In general is has a strong influence on dynamic properties of
controlled system, as well as on whole closed-loop system.
Consider a dynamical system of the first order of the form
T
dy(t)
dt
+ y(t)=u(t) (5.17)
where y(t) is the output variable, u(t) is the input variable, and T is the process
time constant. The sampling period can be chosen based on the relation
T
5
<T
s
<
T
2

5.2 Z – Transform 195
Consider a dynamical system of the second order of the form
T
2
k
d
2
y(t)
dt
2
+2ζT
k
dy(t)
dt
+ y(t)=u(t) (5.18)
where T
k
is its time constant andζ the damping coefficient. The sampling
period is usually chosen within the interval
0.25 ≤
T
s
T
k
< 1.50.7 ≤ ζ ≤ 1 (5.19)
If ζ>1 then an approximate model of the form (5.17) can be used. If
a closed-loop system is considered, the overall damping coefficient should be
larger than 0.7.
5.2 Z – Transform
f
0 t
()
tf
()
tf
∗
()
sF
()
sF
∗
t
0
s
T
s
T2
s
T3
s
T4
s
T5
∗
f
Fig. 5.8. An ideal sampler and an impulse modulated signal
Let us again consider an ideal sampler shown in Fig 5.8. This sampler
implements transformation of a continuous-time signal f(t) to an impulse
modulated signal. Individual impulses appear on the sampler output in the
sampling times kT
s
, k =0, 1, 2,... and are equal to functions f (kT
s
), k =
0, 1, 2,.... This impulse modulated signal containing a sequence of impulses
is denoted by f
∗
(t). The signal f
∗
(t) can be expressed as
f
∗
(t)=
∞
k=0
f(kT
s
)δ(t −kT
s
) (5.20)

196 5 Discrete-Time Process Models
The Laplace transform of this function is
L{f
∗
(t)} = F
∗
(s)=
∞
k=0
f(kT
s
)e
−kT
s
s
(5.21)
Let us introduce a new variable in equation (5.21)
z =e
T
s
s
(5.22)
Then we can write
L{f
∗
(t)} =
∞
k=0
f(kT
s
)z
−k
(5.23)
Z-transform of the signal f(t)orf
∗
(t) is defined by the expression
F (z)=Z{f (t)} =
∞
k=0
f(kT
s
)z
−k
(5.24)
or
Z{f(t)} = F
∗
(s)|
z=e
T
s
s
(5.25)
Z-transform is mathematically equivalent to the Laplace transform and differs
only in the argument. Z-transform exists only if some z exists such that the
series in (5.24) converges.
Consider the unit step function 1(t) defined as
1(t)=
$
1,t≥ 0
0,t<0
(5.26)
Sampled unit step function is given as
f(kT
s
)=1,k≥ 0 (5.27)
and thus
Z{1(t)} =
∞
k=0
z
−k
(5.28)
If |z| > 1 then the series in (5.28) is convergent and Z{1(t)} is
Z{1(t)} =
1
1 −z
−1
(5.29)
or
Z{1(t)} =
z
z −1
(5.30)

5.2 Z – Transform 197
Consider now an exponential function
f(t)=e
−at
1(t) (5.31)
where a =1/T and T is a time constant. Then
L{f
∗
(t)} =
∞
k=0
e
−akT
s
e
−kT
s
s
(5.32)
Its Z-transform is given as
Z
e
−at
1(t)
=
∞
k=0
e
−aT
s
z
−1
k
(5.33)
If
z
−1
e
−aT
s
< 1 then
Z
e
−at
1(t)
=
1
1 −z
−1
e
−aT
s
=
z
z − e
−aT
s
(5.34)
Z-transforms of other functions can be calculated in a similar way. Ta-
ble 5.1 lists some functions and their Laplace and Z transformations.
Z-transform is a linear operation.
Z-transform of a delayed function is given as
Z{f(t −kT
s
)} = z
−k
F (z) (5.35)
where k is a positive integer and f(t)=0fort<0.
For an initial function value holds
lim
k→0
f(kT
s
) = lim
z→∞
z −1
z
F (z) (5.36)
For a final function value holds
lim
k→∞
f(kT
s
) = lim
z→1
(1 −z
−1
)F (z) (5.37)
Reciprocally, given the Z-transform of a function, we can find the function
values in sampling times. The inverse Z-transform is symbolically written as
Z
−1
{F (z)} =[f (0),f(T
s
),f(2T
s
),...] (5.38)
or
Z
−1
{F (z)} =[f (kT
s
)] = f
∗
(t) (5.39)
However, using the inverse Z-transform, only values of f in sampling times
are found. It is not possible to find the sampling time. Also, a unique function
F (z) can be found for several continuous-time functions f(t).
Discrete functions can practically be found from Z-transforms using the
polynomial division or the expansion as a sum of partial fractions.
