Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

158 4 Dynamical Behaviour of Processes

ϕ(ω)=−arctan

2ζT

1 −T

. (4.162)

At the corner frequency ω

=1/T

this gives ϕ(ω)=−90

◦

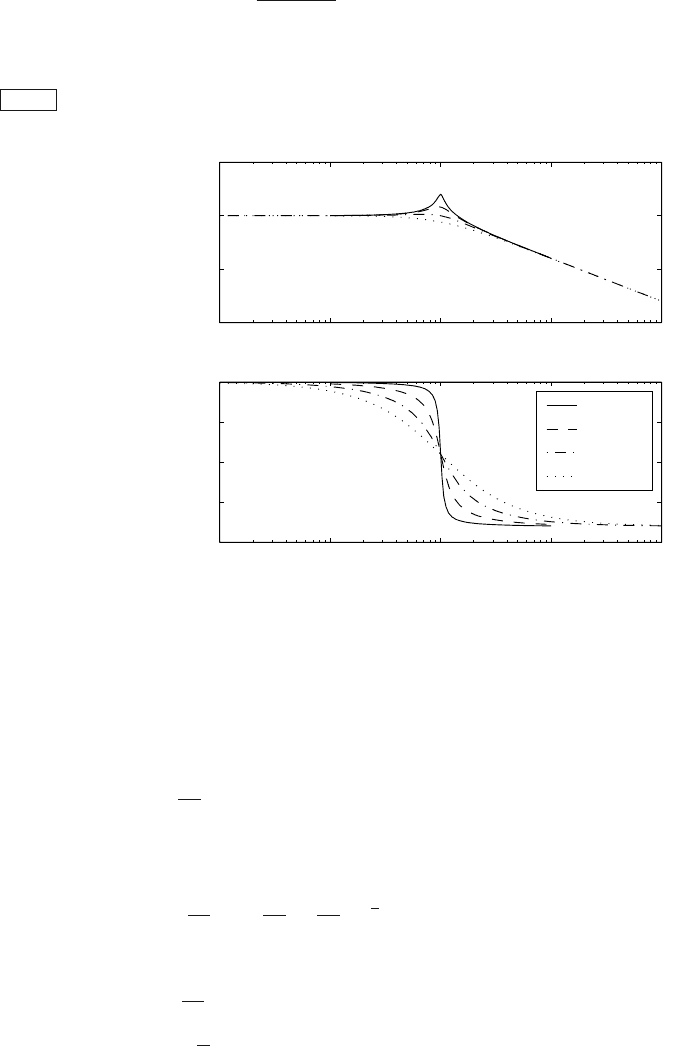
Bode diagrams of the second order systems with Z

=1andT

= 1 min

are shown in Fig. 4.23.

www

−2

−1

−100

−50

Frequency (rad/sec)

Magnitude (dB)

−2

−1

−200

−150

−100

−50

Fre

uenc

(

rad/sec

)

Phase (deg)

ζ=0.05

ζ=0.2

ζ=0.5

ζ=1.0

Fig. 4.23. Bode diagrams of an underdamped second order system (Z

=1,T

=1)

4.3.5 Frequency Characteristics of an Integrator

The transfer function of an integrator is

G(s)=

(4.163)

where Z

=1/T

and T

is the time constant of the integrator.

We note, that integrator is an astatic system. Substitution for s =jω yields

G(jω)=

jω

= −j

−j

. (4.164)

From this follows

A(ω)=

, (4.165)

ϕ(ω)=−

. (4.166)

4.3 Frequency Analysis 159

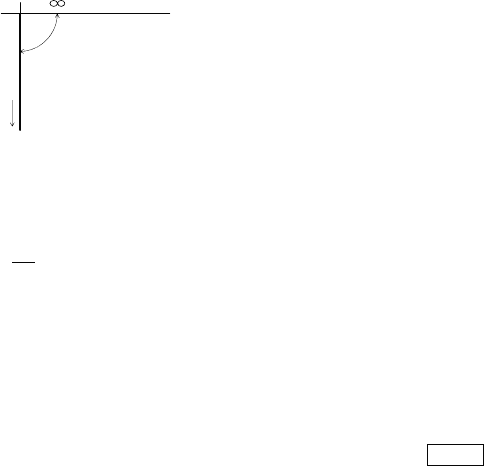
The corresponding Nyquist diagram is shown in Fig. 4.24. The curve co-

incides with the negative imaginary axis. The magnitude is for increasing ω

decreasing. The phase angle is independent of frequency. Thus, output variable

is always delayed to input variable for 90

◦

ω→

Fig. 4.24. The Nyquist diagram of an integrator

Magnitude curve is given by the expression

L(ω) = 20 log A(ω) = 20 log

(4.167)

L(ω) = 20 log Z

− 20 log ω. (4.168)

The phase angle is constant and given by (4.166).

If ω

=10ω

, then

20 log ω

= 20 log 10ω

= 20 + 20 log ω

, (4.169)

thus the slope of magnitude plot is -20dB/decade.

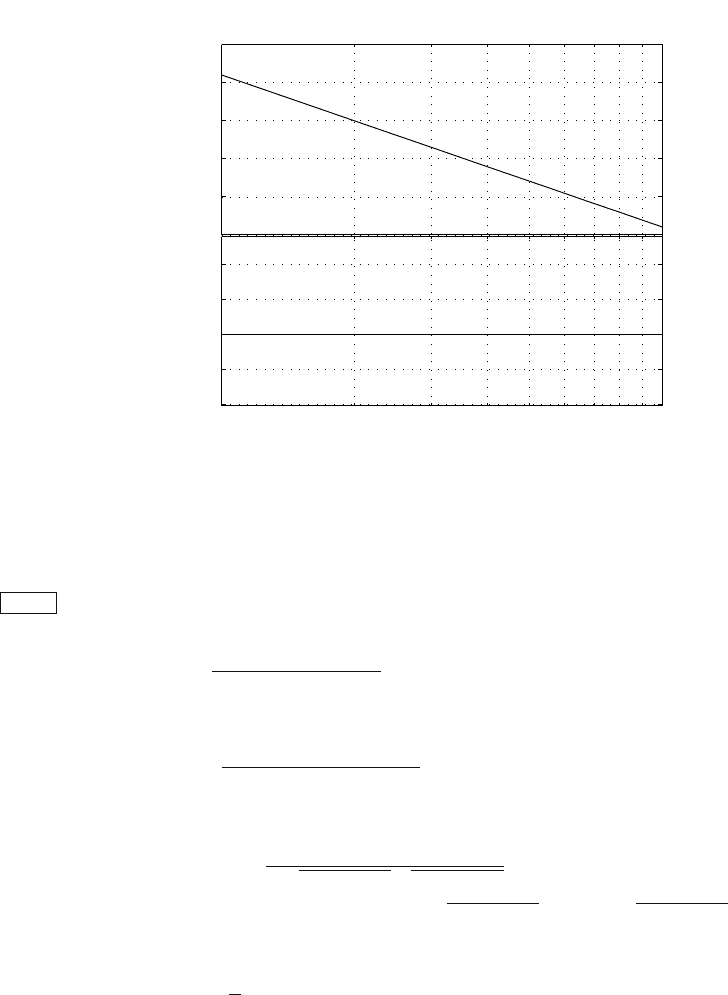
Fig. 4.25 shows Bode diagram of the integrator with T

= 5 s. The values www

of L(ω) are given by the summation of two terms as given by (4.168).

4.3.6 Frequency Characteristics of Systems in a Series

Consider a system with the transfer function

G(s)=G

(s)G

(s) ...G

(s). (4.170)

Its frequency response is given as

G(jω)=

i=1

(ω)e

jϕ

(ω)

(4.171)

G(jω) = exp





i=1

(ω)



i=1

(ω), (4.172)

and

20 log A(ω)=



i=1

20 log A

(ω), (4.173)

ϕ(ω)=



i=1

(ω). (4.174)

160 4 Dynamical Behaviour of Processes

−35

−30

−25

−20

−15

−10

Magnitude (dB)

−91

−90.5

−90

−89.5

−89

Phase (deg)

Bode Diagram

Fre

uenc

(

rad/sec

)

Fig. 4.25. Bode diagram of an integrator

It is clear from the last equations that magnitude and phase angle plots are

obtained as the sum of individual functions of systems in series.

Example 4.8: Nyquist and Bode diagrams for a third order system

www

Consider a system with the transfer function

G(s)=

s(T

s + 1)(T

s +1)

The function G(jω) is then given as

G(jω)=

jω(T

jω + 1)(T

jω +1)

Consequently, for magnitude follows

L(ω) = 20 log



ω)



ω)

= 20 log Z

− 20 log ω − 20 log



ω)

+1− 20 log



ω)

and for phase angle:

ϕ(ω)=−

− arctan(T

ω) −arctan(T

ω)

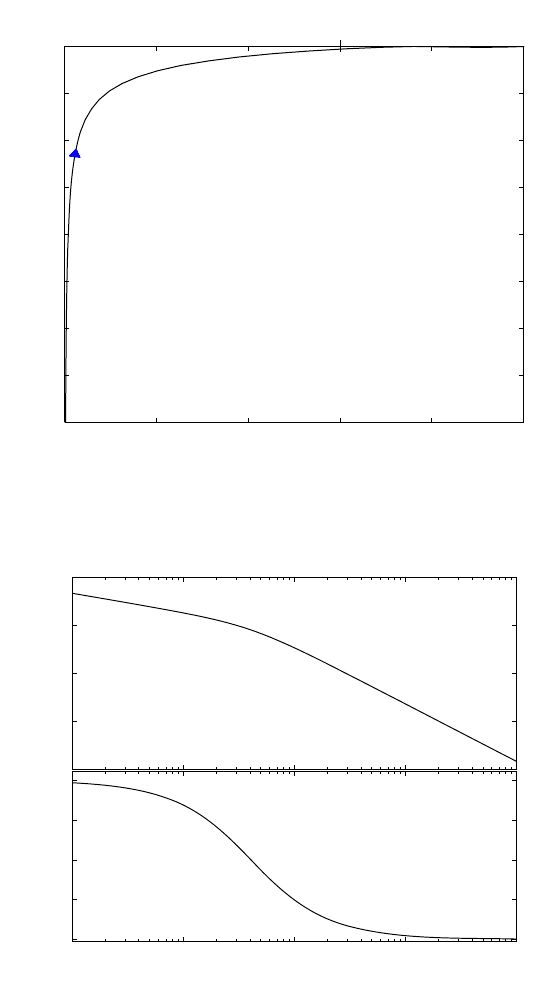
Nyquist and Bode diagrams for the system with Z

=0.5, T

=2s,and

= 3 s are given in Figs. 4.26 and 4.27.

4.3 Frequency Analysis 161

−2.5 −2 −1.5 −1 −0.5 0

−40

−35

−30

−25

−20

−15

−10

−5

Nyquist Diagram

Real Axis

Imaginary Axis

Fig. 4.26. The Nyquist diagram for the third order system

−150

−100

−50

Magnitude (dB)

−2

−1

−270

−225

−180

−135

−90

Phase (deg)

Bode Diagram

Frequency (rad/sec)

Fig. 4.27. Bode diagram for the third order system

162 4 Dynamical Behaviour of Processes

4.4 Statistical Characteristics of Dynamic Systems

Dynamic systems are quite often subject to input variables that are not func-

tions exactly speciﬁed by time as opposed to step, impulse, harmonic or other

standard functions. A concrete (deterministic) time function has at any time

a completely determined value.

Input variables may take diﬀerent random values through time. In these

cases, the only characteristics that can be determined is probability of its

inﬂuence at certain time. This does not imply from the fact that the input

inﬂuence cannot be foreseen, but from the fact that a large number of variables

and their changes inﬂuence the process simultaneously.

The variables that at any time are assigned to a real number by some

statement from a space of possible values are called random.

Before investigating the behaviour of dynamic systems with random inputs

let us now recall some facts about random variables, stochastic processes, and

their probability characteristics.

4.4.1 Fundamentals of Probability Theory

Let us investigate an event that is characterised by some conditions of ex-

istence and it is known that this event may or may not be realised within

these conditions. This random event is characterised by its probability.Let

us assume that we make N experiments and that in m cases, the event A

has been realised. The fraction m/N is called the relative occurrence.Itis

the experimental characteristics of the event. Performing diﬀerent number of

experiments, it may be observed, that diﬀerent values are obtained. However,

with the increasing number of experiments, the ratio approaches some con-

stant value. This value is called probability of the random event A and is

denoted by P (A).

There may exist events with probability equal to one (sure events) and to

zero (impossible events). For all other, the following inequality holds

0 <P(A) < 1 (4.175)

Events A and B are called disjoint if they are mutually exclusive within

the same conditions. Their probability is given as

P (A ∪B)=P (A)+P (B) (4.176)

An event A is independent from an event B if P (A) is not inﬂuenced when

B has or has not occurred. When this does not hold and A is dependent on B

then P(A

) changes if B occurred or not. Such a probability is called conditional

probability and is denoted by P (A|B).

When two events A, B are independent, then for the probability holds

P (A|B)=P (A) (4.177)

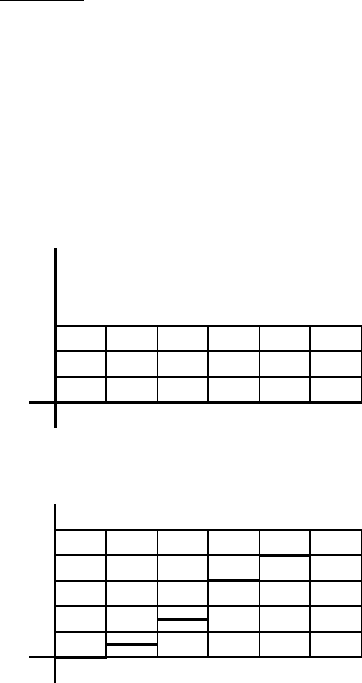
4.4 Statistical Characteristics of Dynamic Systems 163

Let us consider two events A and B where P (B) > 0. Then for the condi-

tional probability P (A|B) of the event A when B has occurred holds

P (A|B)=

P (A ∩B)

P (B)

(4.178)

For independent events we may also write

P (A ∩B)=P (A)P (B) (4.179)

4.4.2 Random Variables

0123456

F (x)

0, 2

0, 4

0, 6

0, 8

0, 1

0, 2

0, 3

Fig. 4.28. Graphical representation of the law of distribution of a random variable

and of the associated distribution function

Let us consider discrete random variables. Any random variable can be as-

signed to any real value from a given set of possible outcomes. A discrete ran-

dom variable ξ is assigned a real value from a ﬁnite set of values x

,...,x

A discrete random variable is determined by the set of ﬁnite values and their

corresponding probabilities P

(i =1, 2,...,n) of their occurrences. The table

ξ =



,...,x

,...,P

(4.180)

164 4 Dynamical Behaviour of Processes

represents the law of distribution of a random variable. An example of the

graphical representation for some random variable is shown in Fig. 4.28a. Here,

the values of probabilities are assigned to outcomes of some random variable

with values x

. The random variable can attain any value of x

(i =1, 2,...,n).

It is easily conﬁrmed that



i=1

= 1 (4.181)

Aside from the law of distribution, we may use another variable that char-

acterises the probability of a random variable. It is denoted by F (x)and

deﬁned as

F (x)=



≤x

(4.182)

and called cumulative distribution function, or simply distribution function of

a variable ξ. This function completely determines the distribution of all real

values of x.Thesymbolx

≤ x takes into account all values of x

less or equal

to x. F (x) is a probability of event ξ ≤ x written as

F (x)=P (ξ ≤ x) (4.183)

Further, F (x) satisﬁes the inequality

0 ≤ F (x) ≤ 1 (4.184)

When the set of all possible outcomes of a random variable ξ is reordered

such that x

≤ x

≤···≤x

, the from the probability deﬁnition follows that

F (x) = 0 for any x<x

. Similarly, F (x) = 1 for any x>x

. Graphical

representation of the distribution function for a random variable in Fig. 4.28a

is shown in Fig. 4.28b.

Although the distribution function characterises a completely random vari-

able, for practical reasons there are also deﬁned other characteristics given by

some non-random values. Among the possible, its expected value, variance,

and standard deviation play an important role.

The expected value of a discrete random variable is given as

μ = E {ξ} =



i=1

(4.185)

In the case of uniform distribution law the expected value (4.185) can be

written as

μ =



i=1

(4.186)

4.4 Statistical Characteristics of Dynamic Systems 165

For a play-cube tossing yields

μ =



i=1

=(1

)=3.5

The properties of the expected value are the following:

Constant Z

E {Z} = Z (4.187)

Multiplication by a constant Z

E {Zξ} = ZE {ξ} (4.188)

Summation

E {ξ + η} = E {ξ} + E {η} (4.189)

Multiplication of independent random variables

E {ξη} = E {ξ}E {η} (4.190)

If ξ is a random variable and μ is its expected value then the variable

(ξ − μ) that denotes the deviation of a random variable from its expected

value is also a random variable.

Variance of a random variable ξ is the expected value of the squared

deviation (ξ − μ)

= D[ξ]=E



(ξ −μ)





i=1

− μ)

(4.191)

Whereas the expected value is a parameter in the neighbourhood of which all

values of a random variable are located, variance characterises the distance

of the values from μ. If the variance is small, then the values far from the

expected value are less probable.

Variance can easily be computed from the properties of expected value:

= E



− 2ξE {ξ} +(E {ξ})



= E





− (E {ξ})

, (4.192)

i.e. variance is given as the diﬀerence between the expected value of the

squared random variable and squared expected value of random variable. Be-

cause the following holds always





≥ (E {ξ})

, (4.193)

variance is always positive, i.e.

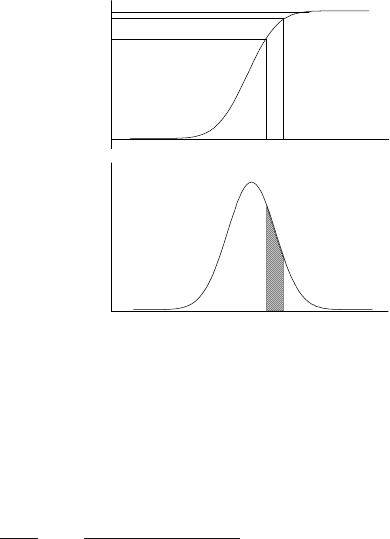
166 4 Dynamical Behaviour of Processes

f(x)

F(a)

F(b)

F(x)

Fig. 4.29. Distribution function and corresponding probability density function of

a continuous random variable

≥ 0 (4.194)

The square root of the variance is called standard deviation of a random

variable

σ =



D[ξ]=



E {ξ

}−(E {ξ})

(4.195)

A continuous random variable can be assigned to any real value within

some interval if its distribution function F (x) is continuous on this interval.

The distribution function of a continuous random variable ξ

F (x)=P (ξ<x) (4.196)

is the probability the random variable is less than x. A typical plot of such a

distribution function is shown in Fig. 4.29a. The following hold for F (x):

lim

x→∞

F (x) = 1 (4.197)

lim

x→−∞

F (x) = 0 (4.198)

The probability that a random variable attains some speciﬁed value is in-

ﬁnitesimally small. On the contrary, the probability of random variable lying

in a some interval (a, b) is ﬁnite and can be calculated as

P (a ≤ ξ<b)=F (b) −F (a) (4.199)

The probability that a continuous random variable is between x and x+dx

is given as

4.4 Statistical Characteristics of Dynamic Systems 167

P (x ≤ ξ<x+dx)=

dF (x)

dx (4.200)

where the variable

f(x)=

dF (x)

(4.201)

is called probability density. Figure 4.29b shows an example of f(x). Thus, the

distribution function F (x) may be written as

F (x)=



−∞

f(x)dx (4.202)

Because F (x) is non-decreasing, the probability density function must be

positive

f(x) ≥ 0 (4.203)

The probability that a random variable is within an interval (a, b) calculated

from its density function is given as the surface under curve f(x) within the

given interval. Thus, we can write

P (a ≤ ξ<b)=



f(x)dx (4.204)

Correspondingly, when the interval comprises of all real values, yields



∞

−∞

f(x)dx = 1 (4.205)

Expected value of a continuous random variable is determined as

μ = E {ξ} =



∞

−∞

xf(x)dx (4.206)

A random variable can be characterised by the equation

E {ξ

} =



∞

−∞

f(x)dx (4.207)

which determines m-th moment of a random variable ξ. The ﬁrst moment is

the expected value. The second moment is given as







∞

−∞

f(x)dx (4.208)

Central m-th moment is of the form

E {(ξ − μ)

} =



∞

−∞

(x −μ)

f(x)dx (4.209)