Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


148 4 Dynamical Behaviour of Processes
If the sine wave is continued for a long time, the exponential term disap-
pears and the remaining terms can be further manipulated to yield
y(t)=
Z
1
A
1
−2ωT
1
− 2j
−2ωT
1
+2j
−2ωT
1
+2j
e
−jωt
+
Z
1
A
1
−2ωT
1
+2j
−2ωT
1
− 2j
−2ωT
1
− 2j
e
jωt
(4.104)
y(t)=Z
1
A
1
−ωT
1
+j
2(ω
2
T
2
1
+1)
e
−jωt
+
−ωT
1
− j
2(ω
2
T
2
1
+1)
e
jωt
(4.105)
y(t)=Z
1
A
1
−ωT
1
(ω
2
T
2
1
+1)
e
−jωt
+e
jωt
2
+
1
(ω
2
T
2
1
+1)
e
jωt
− e
−jωt
2
(4.106)
Applying the Euler identities (3.15) yields
y(t)=Z
1
A
1
−
ωT
1
ω
2
T
2
1
+1
cos ωt +
1
ω
2
T
2
1
+1
sin ωt
(4.107)
Finally, using the trigonometric identity
sin(ωt + ϕ)=sinϕ cos ωt +cosϕ sin ωt
gives
y(t)=Z
1
A
1
-
ω
2
T
2
1
+1
ω
2
T
2
1
+1
sin(ωt + ϕ)
.
(4.108)
where ϕ = −arctan ωT
1
.
If we set in (4.97) s =jω, then
G(jω)=
Z
1
T
1
jω +1
(4.109)
|G(jω)| =
Z
1
ω
2
T
2
1
+1
(4.110)
which is the same as the amplitude in (4.108) divided by A
1
.Thusy(t)can
also be written as
y(t)=A
1
|G(jω)|sin(ωt + ϕ) (4.111)
It follows from (4.108) that the output amplitude is a function of the input
amplitude A
1
, input frequency ω, and the system properties. Thus,
A
1
|G(jω)| = A
1
f(ω, Z
1
,T
1
). (4.112)
For the given system with the constants Z
1
and T
1
, it is clear that increasing
input frequency results in decreasing output amplitude. The phase lag is given
as
ϕ = −arctan T
1
ω (4.113)
and the influence of the input frequency ω to ϕ is opposite to amplitude.
The simulation of u(t)andy(t) from the equations (4.98) and (4.108) for
www
Z
1
=0.4, T
1
=5.2 min, A
1
=5
◦
C,andω =0.2 rad/min is shown in Fig. 4.17.
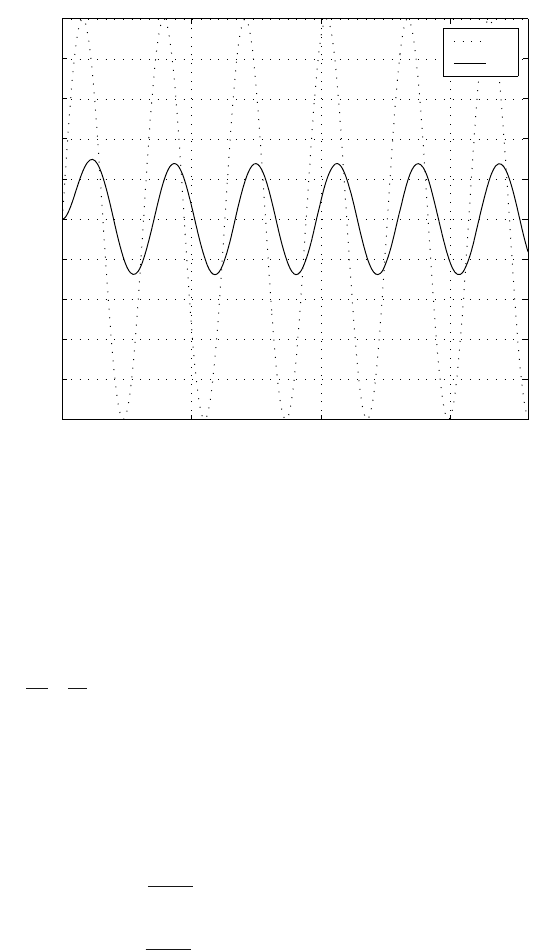
4.3 Frequency Analysis 149
0 50 100 150
−5
−4
−3
−2
−1
0
1
2
3
4
5
t [min]
u [°C] y[°C]
u
y
Fig. 4.17. Ultimate response of the heat exchanger to sinusoidal input
4.3.2 Definition of Frequency Responses
A time periodic function f(t) with the period T
f
satisfying the Dirichlet con-
ditions can be expanded into the Fourier expansion
f(t)=
2
T
f
-
a
0
2
+
∞
n=1
(a
n
cos nω
f
t + b
n
sin nω
f
t)
.
(4.114)
where ω
f
=2π/T
f
is the basic circular frequency. The coefficients a
0
, a
n
, b
n
,
(n =1, 2,...) are given as
a
0
=
T
f
/2
−T
f
/2
f(τ )dτ
a
n
=
T
f
/2
−T
f
/2
f(τ )cos
2πnτ
T
f
dτ
b
n
=
T
f
/2
−T
f
/2
f(τ )sin
2πnτ
T
f
dτ
Using the Euler identity, the Fourier expansion can be rewritten as
f(t)=
∞
n=−∞
c
n
e
jnω
f
t
(4.115)

150 4 Dynamical Behaviour of Processes
where
c
n
=
1
T
f
T
f
/2
−T
f
/2
f(τ )e
−jnω
f
τ
dτ
Any nonperiodic time function can be assumed as periodic with the period
approaching infinity. If we define ω = nω
f
then
f(t)=
1
2π
∞
n=−∞
$
T
f
/2
−T
f
/2
f(τ )e
−jωτ
dτ
%
e
jωt
[(n +1)ω
f
− nω
f
] (4.116)
If T
f
→∞and [(n +1)ω
f
− nω
f
]=Δω
f
→ 0 then
f(t)=
1
2π
∞
−∞
F (jω)e
jωt
dω (4.117)
or
F (jω)=
∞
−∞
f(t)e
−jωt
dt (4.118)
The equations (4.117), (4.118) are the Fourier integral equations that de-
scribe the influence between the original time function and its frequency trans-
form F (jω). Compared to the Fourier expansion they describe an expansion
to the continuous spectrum with the infinitesimally small difference dω of two
neighbouring harmonic signals.
The integral (4.118) expresses a transformation (or operator) that assigns
to the function f (t) the function F (jω). This transformation is called the
Fourier transform of f(t). If we know the transformed F (jω), the original
function f(t) can be found from (4.117) by the inverse Fourier transform.
The important condition of the Fourier transform is the existence of the inte-
grals (4.117), (4.118).
Complex transfer function,orfrequency transfer function G(jω)isthe
Fourier transform corresponding to the transfer function G(s). For G(jω) holds
G(jω)=
Y (jω)
U(jω)
(4.119)
If the frequency transfer function exists, it can be easily obtained from the
system transfer function by formal exchange of the argument s,
G(jω)=G(s)
s=jω
(4.120)
or
G(jω)=
b
m
(jω)
m
+ b
m−1
(jω)
m−1
+ ···+ b
0
a
n
(jω)
n
+ b
n−1
(jω)
n−1
+ ···+ a
0
(4.121)

4.3 Frequency Analysis 151
The frequency transfer function of a singlevariable system can be obtained
from
G(jω) ≡
∞
0
g(t)e
−jωt
dt. (4.122)
Analogously, for multivariable systems follows
G(jω) ≡
∞
0
g(t)e
−jωt
dt. (4.123)
If the transfer function matrix G(s) is stable, then frequency transfer
function matrix exists as the Fourier transform of the impulse response matrix
and can be calculated from (see equations (3.46), (4.8))
G(jω)=C(jωI − A)
−1
B + D (4.124)
Frequency transfer function is a complex variable corresponding to a real
variable ω that characterises the forced oscillations of the output y(t) for the
harmonic input u(t) with frequency ω. Harmonic functions can be mathemat-
ically described as
¯u = A
1
e
j(ωt+ϕ
1
)
(4.125)
¯y = A
2
e
j(ωt+ϕ
2
)
. (4.126)
The ratio of these functions is a complex variable G(jω) defined by (4.122).
Thus it can be written as
¯y
¯u
=
A
2
A
1
e
j(ϕ
2
−ϕ
1
)
= G(jω). (4.127)
The magnitude of G(jω)
|G(jω)| = A(ω) (4.128)
is given as the ratio A
2
/A
1
of output and input variable magnitudes. The
phase angle
ϕ(ω)=ϕ
2
− ϕ
1
(4.129)
is determined as the phase shift between the output and input variable and is
given in units of radians as a function of ω. G(jω) can be written in the polar
form
G(jω)=A(ω)e
jϕ(ω)
(4.130)
The graph of G(jω)
G(jω)=|G(jω)|e
jargG(jω)
= [G(jω)] + j[G(jω)] (4.131)

152 4 Dynamical Behaviour of Processes
in the complex plane is called the Nyquist diagram. The magnitude and phase
angle can be expressed as follows:
|G(jω)| =
{[G(jω)]}
2
+ {[G(jω)]}
2
(4.132)
|G(jω)| =
G(jω)G(−jω) (4.133)
tan ϕ =
[G(jω)]
[G(jω)]
(4.134)
ϕ = arctan
[G(jω)]
[G(jω)]
(4.135)
Essentially, the Nyquist diagram is a polar plot of G(jω) in which frequency
ω appears as an implicit parameter.
The function A = A(ω) is called magnitude frequency response and the
function ϕ = ϕ(ω) phase angle frequency response. Their plots are usually
given with logarithmic axes for frequency and magnitude and are referred to
as Bode plots.
Let us investigate the logarithm of A(ω)exp[jϕ(ω)]
ln G(jω)=lnA(ω)+jϕ(ω) (4.136)
The function
ln A(ω)=f
1
(log ω) (4.137)
defines the magnitude logarithmic amplitude frequency response and is shown
in the graphs as
L(ω) = 20 log A(ω)=200.434 ln A(ω). (4.138)
L is given in decibels (dB) which is the unit that comes from the acoustic
theory and merely rescales the amplitude ratio portion of a Bode diagram.
Logarithmic phase angle frequency response is defined as
ϕ(ω)=f
2
(log ω) (4.139)
Example 4.7: Nyquist and Bode diagrams for the heat exchanger as the first
www
order system
The process transfer function of the heat exchanger was given in (4.97).
G(jω) is given as
G(jω)=
Z
1
T
1
jω +1
=
Z
1
(T
1
jω − 1)
(T
1
jω)
2
+1
=
Z
1
(T
1
ω)
2
+1
− j
Z
1
T
1
ω
(T
1
ω)
2
+1
=
Z
1
(T
1
ω)
2
+1
e
−j arctan T
1
ω
The magnitude and phase angle are of the form

4.3 Frequency Analysis 153
A(ω)=
Z
1
(T
1
ω)
2
+1
ϕ(ω)=−arctan T
1
ω
Nyquist and Bode diagrams of the heat exchanger for Z
1
=0.4, T
1
=5.2s
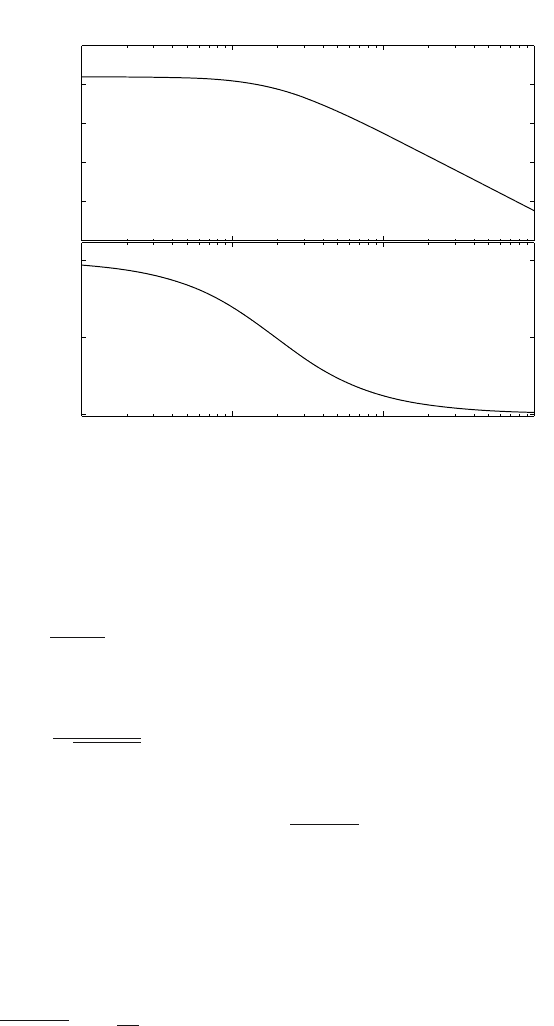
are shown in Figs. 4.18, 4.19, respectively.
0 0.1 0.2 0.3 0.4 0.5
−0.25
−0.2
−0.15
−0.1
−0.05
0
Nyquist Diagram
Real Axis
Imaginary Axis
Fig. 4.18. The Nyquist diagram for the heat exchanger
4.3.3 Frequency Characteristics of a First Order System
In general, the dependency [G(jω)] on [G(jω)] for a first order system
described by (4.97) can easily be found from the equations
u = [G(jω)] =
Z
1
(T
1
ω)
2
+1
(4.140)
v = [G(jω)] = −
Z
1
T
1
ω
(T
1
ω)
2
+1
(4.141)
Equating the terms T
1
ω in both equations yields
(v − 0)
2
−
u −
Z
1
2
=
Z
1
2
2
(4.142)
154 4 Dynamical Behaviour of Processes
−50
−40
−30
−20
−10
0
Magnitude (dB)
10
−2
10
−1
10
0
10
1
−90
−45
0
Phase (deg)
Bode Diagram
Fre
q
uenc
y
(
rad/sec
)
Fig. 4.19. The Bode diagram for the heat exchanger
which is the equation of a circle.
Let us denote ω
1
=1/T
1
. The transfer function (4.97) can be written as
G(s)=
ω
1
Z
1
s + ω
1
. (4.143)
The magnitude is given as
A(ω)=
Z
1
ω
1
ω
2
1
+ ω
2
(4.144)
and its logarithm as
L = 20 log Z
1
+ 20 log ω
1
− 20 log
/
ω
2
1
+ ω
2
. (4.145)
This curve can easily be sketched by finding its asymptotes. If ω approaches
zero, then
L → 20 log Z
1
(4.146)
and if it approaches infinity, then
/
ω
2
1
+ ω
2
→
√
ω
2
(4.147)
L → 20 log Z
1
+ 20 log ω
1
− 20 log ω. (4.148)
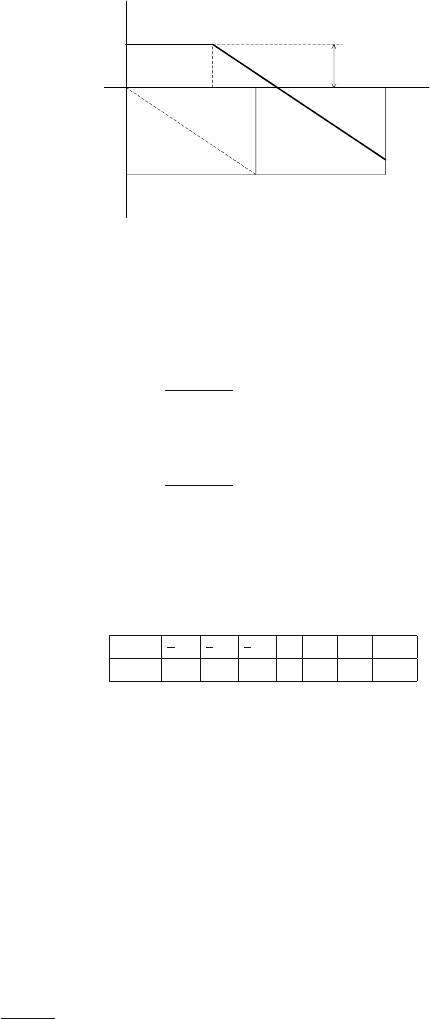
4.3 Frequency Analysis 155
0
-20
1
10
100
L [dB]
ω
[rad/s]
20 log Z
1
ω
1
Fig. 4.20. Asymptotes of the magnitude plot for a first order system
This is the equation of an asymptote that for ω = ω
1
is equal to 20 log Z
1
.
The slope of this asymptote is -20 dB/decade (Fig 4.20).
The asymptotes (4.146) and (4.148) introduce an error δ for ω<ω
1
:
δ = 20 log ω
1
− 20 log
/
ω
2
1
+ ω
2
(4.149)
and for ω>ω
1
:
δ = 20 log ω
1
− 20 log
/
ω
2
1
+ ω
2
− [20 log ω
1
− 20 log ω] (4.150)
The tabulation of errors for various ω is given in Table 4.2.
Table 4.2. The errors of the magnitude plot resulting from the use of asymptotes
ω
1
5
ω
1
1
4
ω
1
1
2
ω
1
ω
1
2ω
1
4ω
1
5ω
1
δ(dB) 0.17 -0.3 -1 -3 -1 -0.3 -0.17
A phase angle plot can also be sketched using asymptotes and tangent in
its inflex point (Fig 4.21).
We can easily verify the following characteristics of the phase angle plot:
If ω = 0, then ϕ =0,
If ω = ∞, then ϕ = −π/2,
If ω =1/T
1
, then ϕ = −π/4,
and it can be shown that the curve has an inflex point at ω = ω
1
=1/T
1
.
This frequency is called the corner frequency. The slope of the tangent can be
calculated if we substitute for ω =10
z
(log ω = z)intoϕ = arctan(−T
1
ω):
˙ϕ =
1
1+x
2
,x= −T
1
ω
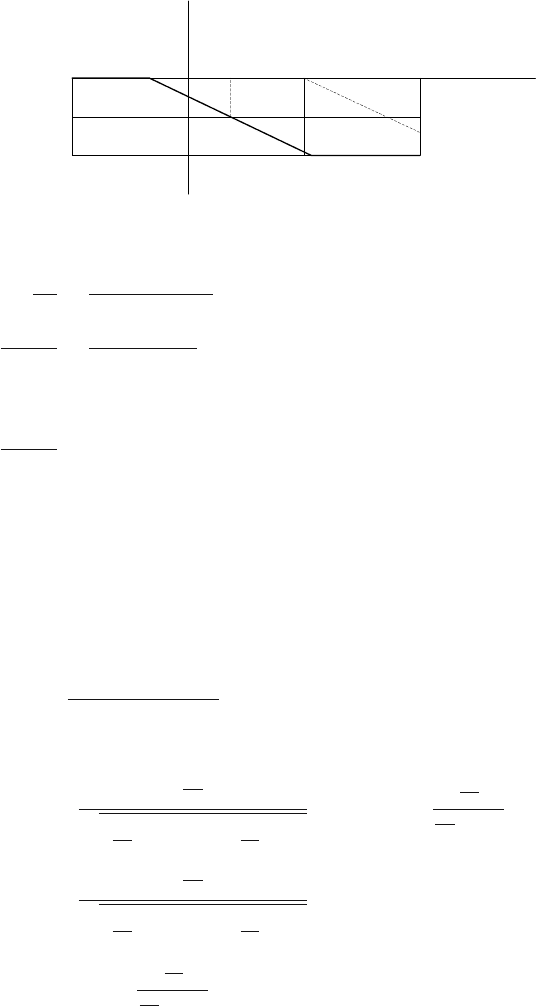
156 4 Dynamical Behaviour of Processes
0
-
π
/2
1
10
100
ϕ
ω
1
ω
-
π
/4
[rad/s]
Fig. 4.21. Asymptotes of phase angle plot for a first order system
dϕ
dz
=
−2.3
1+(−T
1
10
z
)
2
T
1
10
z
dϕ
d log ω
=
−2.3
1+(−T
1
ω)
2
T
1
ω
for ω =1/T
1
dϕ
d log ω
= −1.15 rad/decade
-1.15 rad corresponds to −66
◦
. The tangent crosses the asymptotes ϕ =0and
ϕ = −π/2 with error of 11
◦
40
.
4.3.4 Frequency Characteristics of a Second Order System
Consider an underdamped system of the second order with the transfer
function
G(s)=
1
T
2
k
s
2
+2ζT
k
s +1
,ζ<1. (4.151)
Its frequency transfer function is given as
G(jω)=
1
T
2
k
0
1
T
2
k
− ω
2
2
+
2ζ
T
k
2
ω
2
exp
j arctan
−
2ζ
T
k
ω
1
T
2
k
− ω
2
(4.152)
A(ω)=
1
T
2
k
0
1
T
2
k
− ω
2
2
+
2ζ
T
k
2
ω
2
(4.153)
ϕ(ω) = arctan
−
2ζ
T
k
ω
1
T
2
k
− ω
2
. (4.154)
The magnitude plot has a maximum for ω = ω
k
where T
k
=1/ω
k
(resonant
frequency). If ω = ∞, A = 0. The expression

4.3 Frequency Analysis 157
M =
A(ω
k
)
A(0)
=
A
max
A(0)
(4.155)
is called the resonance coefficient.
If the system gain is Z
1
, then
L(ω) = 20 log |G(jω)| = 20 log
Z
1
(jω)
2
ω
2
k
+2
ζ
ω
k
jω +1
(4.156)
L(ω) = 20 log
Z
1
T
2
k
(jω)
2
+2ζT
k
jω +1
(4.157)
L(ω) = 20 log Z
1
− 20 log
/
(1 −T
2
k
ω
2
)
2
+(2ζT
k
ω)
2
(4.158)
It follows from (4.158) that the curve L(ω)forZ
1
= 1 is given by summation
of 20 log Z
1
to normalised L for Z
1
= 1. Let us therefore investigate only the
case Z
1
= 1. From (4.158) follows
L(ω)=−20 log
/
(1 −T
2
k
ω
2
)
2
+(2ζT
k
ω)
2
. (4.159)
In the range of low frequencies (ω 1/T
k
) holds approximately
L(ω) ≈−20 log
√
1=0. (4.160)
For high frequencies (ω 1/T
k
)andT
2
k
ω
2
1and(2ζT
k
ω)
2
(T
2
k
ω
2
)
2
holds
L(ω) ≈−20 log(T
k
ω)
2
= −2 20 log T
k
ω = −40 log T
k
ω. (4.161)
Thus, the magnitude frequency response can be approximated by the curve
shown in Fig 4.22. Exact curves deviate with an error δ from this approxima-
tion. For 0.38 ≤ ζ ≤ 0.7 the values of δ are maximally ±3dB.
0
-40
1
10
100
L [dB]
ω
ω = 1/Τ
k
k
[rad/s]
Fig. 4.22. Asymptotes of magnitude plot for a second order system
The phase angle plot is described by the equation
