Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


128 4 Dynamical Behaviour of Processes
x(t +Δt)=x(t)+Δt ˙x(t)+
1
2
(Δt)
2
¨x(t)+··· (4.36)
If the solved differential equation is of the form
dx(t)
dt
= f(t, x(t)) (4.37)
then the time derivatives can be expressed as
˙x(t)=f(t, x(t))
¨x(t)=
df
dt
=
∂f
∂t
+
∂f
∂x
dx
dt
=
∂f
∂t
+
∂f
∂x
f (4.38)
.
.
.
Substituting (4.38) into (4.36) yields
x(t +Δt)=x(t)+Δtf +
1
2
(Δt)
2
(f
t
+ f
x
f)+··· (4.39)
where f = f (t, x(t)), f
t
= ∂f/∂t, f
x
= ∂f/∂x.
The solution x(t+Δt) in Eq. (4.39) depends on the knowledge of derivatives
of the function f. However, the higher order derivatives of f are difficult to
obtain. Therefore only some first terms of (4.39) are assumed to be significant
and others are neglected. The Taylor expansion is truncated and forms the
basis for Runge-Kutta methods. The number of terms determines order of the
Runge-Kutta method.
Assume that the integration step is given as
t
k+1
= t
k
+ h (4.40)
The second order Runge-Kutta method is based on the difference equation
x(t
k+1
)=x(t
k
)+h ˙x(t
k
)+
1
2
h
2
¨x(t
k
) (4.41)
or
x
k+1
= x
k
+ hf
k
+
1
2
h
2
(f
t
+ f
x
f)
k
(4.42)
The recursive relation suitable for numerical solution is then given by
x
k+1
= x
k
+ γ
1
k
1
+ γ
2
k
2
(4.43)
where γ
1
,γ
2
are weighting constants and
k
1
= hf(t
k
,x
k
) (4.44)
k
2
= hf(t
k
+ α
1
h, x
k
+ β
1
k
1
) (4.45)
4.2 Computer Simulations 129
and α
1
,α
2
are some constants. The proof that (4.43) is a recursive solution
following from the second order Runge-Kutta method can be shown as follows.
Allow at first perform the Taylor expansion for k
2
k
2
= h[f
k
+(f
t
)
k
α
1
h +(f
x
)
k
β
1
hf
k
+ ···] (4.46)
and neglect all terms not explicitly given. Substituting k
1
from (4.44) and k
2
from (4.46) into (4.43) gives
x
k+1
= x
k
+ h(γ
1
f
k
+ γ
2
f
k
)+h
2
[γ
2
α
1
(f
t
)
k
+ γ
2
β
1
(f
x
)
k
f
k
] (4.47)
Comparison of (4.41) and (4.47) gives
γ
1
+ γ
2
= 1 (4.48)
γ
2
α
1
=
1
2
(4.49)
γ
2
β
1
=
1
2
(4.50)
This showed that (4.43) is a recursive solution that follows from the second
order Runge-Kutta method.
The best known recursive equations suitable for a numerical solution of
differential equations is the fourth order Runge-Kutta method that is of the
form
x
k+1
= x
k
+
1
6
k
1
+
1
3
k
2
+
1
3
k
3
+
1
6
k
4
(4.51)
where
k
1
= hf(t
k
,x
k
)
k
2
= hf(t
k
+
1
2
h, x
k
+
1
2
k
1
)
k
3
= hf(t
k
+
1
2
h, x
k
+
1
2
k
2
)
k
4
= hf(t
k
+ h, x
k
+ k
3
)
(4.52)
4.2.3 Runge-Kutta Method for a System of Differential Equations
The Runge-Kutta method can be used for the solution of a system of differ-
ential equations
dx(t)
dt
= f(t, x(t)), x(t
0
)=x
0
(4.53)
where x =(x
1
,...,x
n
)
T
.
Vectorised equivalents of equations (4.41), (4.43), (4.44), (4.45) are as
follows
x(t
k+1
)=x(t
k
)+h
˙
x(t
k
)+
1
2
h
2
¨
x(t
k
) (4.54)
x
k+1
= x
k
+ γ
1
k
1
+ γ
2
k
2
(4.55)
k
1
= hf(t
k
, x
k
) (4.56)
k
2
= hf(t
k
+ α
1
h, x
k
+ β
1
k
1
) (4.57)

130 4 Dynamical Behaviour of Processes
The programs for implementation of the fourth order Runge-Kutta method
in various computer languages are given in the next example.
Example 4.6: Programs for the solution of state-space equations
www
We will explain the use of the fourth order Runge-Kutta method applied
to the following second order differential equation
T
1
T
2
d
2
y
2
dt
2
+(T
1
+ T
2
)
dy
2
dt
+ y
2
= Z
1
u
with zero initial conditions and for u(t)=1(t). T
1
,T
2
are time constants
and Z
1
gain of this system. At first we transform this differential equation
into state-space so that two differential equations of the first order result
dx
1
dt
=
Z
1
u −x
2
− (T
1
+ T
2
)x
1
T
1
T
2
dx
2
dt
= x
1
The program written in GW-BASIC is given in Program 4.1. The state-
space differential equations are defined on lines 550, 560. The solution y
1
(t)=
x
1
(t), y
2
(t)=x
2
(t) calculated with this program is given in Table 4.1. The
values of variable y
2
(t) represent the step response of the system with transfer
function
G(s)=
Y (s)
U(s)
=
Z
1
(T
1
s + 1)(T
2
s +1)
Program 4.2 is written in C. The example of the solution in the simula-
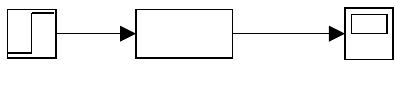
tion environment MATLAB/Simulink is given in Program 4.3. This represents
m-file that can be introduced as S-function into Simulink block scheme shown
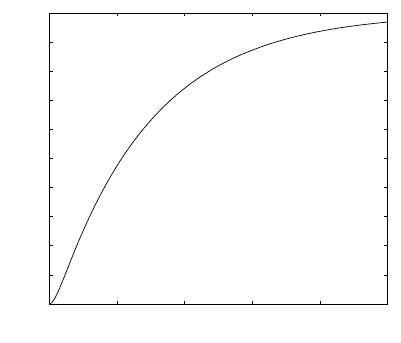
in Fig. 4.9. The graphical solution is then shown in Fig. 4.10 and it is the same
as in Tab. 4.1.
Program 4.1 (Simulation program in GW-BASIC)
5 REM ruku4.bas
10 REM solution of the ODE system
20 REM n number of equations
30 REM h integration step
50 REM y(1),y(2),...,y(n) initial conditions
55 DATA 2: READ n
58 DIM y(n), x(n), f(n), k(4, n)
60 DATA .5, 0, 0
70 READ h
80 FOR i = 1 TO n: READ y(i): NEXT i
140 PRINT "t", "y1", "y2"
160 PRINT t, y(1), y(2)
200 FOR k = 0 TO 19
205 FORi=1TOn:x(i) = y(i): NEXT i: GOSUB 470
4.2 Computer Simulations 131
240 FORi=1TOn
242 k(1, i) = h * f(i) : x(i) = y(i) + k(1, i) / 2
244 NEXT i: GOSUB 470
290 FORi=1TOn
292 k(2, i) = h * f(i): x(i) = y(i) + k(2, i) / 2
294 NEXT i: GOSUB 470
340 FORi=1TOn
342 k(3, i) = h * f(i): x(i) = y(i) + k(3, i)
344 NEXT i: GOSUB 470
390 FORi=1TOn
392 k(4, i) = h * f(i)
410 y(i) = y(i)+(k(1,i)+2*k(2,i)+2*k(3,i)+k(4,i)) /6
420 NEXT i
430 t=t+h
440 PRINT t, y(1), y(2)
450 NEXT k
460 END
470 REM assignments
480 z1 = 1: te1 = 1: te2 = 2
510 u = 1
520 x1 = x(1): x2 = x(2)
540 REM funkcie
550 f(1) = (z1 *u-x2-(te1 + te2) * x1) / (te1 * te2)
560 f(2) = x1
570 RETURN
Program 4.2 (Simulation program in C)
#include <stdio.h>
void rk45 (rouble *u,rouble *y, rouble *f, rouble dt);
void fun(rouble y[], rouble f[], rouble u[]);
#define N 2 /* number of ODEs */
int main(void)
{
rouble t=0, tend=10, dt=0.5;
rouble y[N], u[1];
rouble f[N];
u[0]=1;y[0]=0;y[1]=0;
printf("%f %f %f\n",t, y[0],y[1]);
do{
rk45 (u, y, f, dt);
t+=dt;
132 4 Dynamical Behaviour of Processes
printf("%f %f %f\n",t, y[0],y[1]);
}while (t<tend);
return 0;
}
void fun(rouble y[], rouble f[], rouble u[])
{
static rouble te1=1, te2=2, z=1;
f[0]=(z*u[0]-y[1]-(te1+te2)*y[0])/(te1*te2);
f[1]=y[0];
}
void rk45 (rouble *u, rouble *y, rouble *f, rouble dt)
{
int i,j;
rouble yold[N], fh[4*N];
for (i=0 ; i<N ; i++)
yold[i]=y[i];
for(i=0; i<4; i++){
fun(y, f, u);
for(j=0;j<N; j++){
fh[i*N+j]=dt*f[j];
if(i<2) y[j]=yold[j]+0.5*fh[i*N+j];
if(i==2) y[j]=yold[j]+fh[i*N+j];
}
}
for(i=0; i<N; i++)
y[i]=yold[i]+(fh[i]+2.0*(fh[N+i]+fh[2*N+i])+fh[3*N+i])/6.0;
}
Program 4.3 (Source code in MATLAB)
function [sys,x0,str,ts] = simss(t,x,u,flag)
z1 = 1;
te1 = 1;
te2 = 2;
den = 1/(te1 * te2);
A = [-(te1+te2)/den -1/den
1 0];
B = [z1/den; 0];
C=[10;01];
4.2 Computer Simulations 133
switch flag,
case 0
[sys,x0,str,ts] = mdlInitializeSizes;
case 1,
sys = mdlDerivatives(t,x,u,A,B);
case 3,
sys = mdlOutputs(t,x,u,C);
case 9
sys = [];
end
function [sys,x0,str,ts] = mdlInitializeSizes()
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0; 0];
str = [];
ts = [0 0];
function sys = mdlDerivatives(t,x,u,A,B)
sys = A*x + B*u;
function sys = mdlOutputs(t,x,u,C)
sys = C*x;
Step
Scope
simss
S−Function
Fig. 4.9. Simulink block scheme
134 4 Dynamical Behaviour of Processes
0 2 4 6 8 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t
y
Fig. 4.10. Results from simulation
Table 4.1. Solution of the second order differential equation
ty1 y2
00 0
.5 .1720378 .0491536
1 .238372 .1550852
1.5 .2489854 .2786338
2 .2323444 .3997614
2.5 .2042715 .5092093
3 .1732381 .6036183
3.5 .1435049 .6827089
4 .1169724 .7476815
4.5 .0926008 .8003312
5 .07532854 .8425783
5.5 .05983029 .8762348
6 .04730249 .9029045
6.5 .03726806 .9239527
7 .02928466 .9405137
7.5 .02296489 .9535139
8 .01798097 .9637005
8.5 .01406181 .9716715
9 .01098670 .9779023
9.5 .00857792 .9827687
10 .00669353 .9865671
4.2 Computer Simulations 135
4.2.4 Time Responses of Liquid Storage Systems
Consider the liquid storage system shown in Fig. 2.1. Assume its mathematical
model in the form
F
1
dh
1
dt
+ c
1
h
1
+ c
2
h
1
= q
0
(4.58)
where c
1
and c
2
are constants obtained from measurements on a real process.
The steady-state is given by the following equation
c
1
h
s
1
+ g(h
s
1
)=q
s
0
, where g(h
s
1
)=c
2
h
s
1
(4.59)
Let us introduce the deviation variables
x
1
= h
1
− h
s
1
u
1
= q
0
− q
s
0
(4.60)
The mathematical model can then be rewritten as
F
1
dx
1
dt
+ c
1
x
1
+ c
1
h
s
1
+ c
2
x
1
+ h
s
1
= u
1
+ q
s
0
(4.61)
Substracting (4.58) from (4.61) yields
F
1
dx
1
dt
+ c
1
x
1
+ c
2
x
1
+ h
s
1
− c
2
h
s
1
= u
1
(4.62)
Let us introduce the function
G(x
1
)=g(x
1
+ h
s
1
) −g(h
s
1
) (4.63)
then the mathematical model is finally given with deviation variables as
F
1
dx
1
dt
+ c
1
x
1
+ G(x
1
)=u
1
(4.64)
www
The Simulink block scheme that uses the MATLAB file hs11m.m (Pro-
gram 4.4) as the S-function for solution of Eq. (4.64) is shown in Fig.4.11.
Program 4.4 (MATLAB file hs11m.m)
function [sys,x0,str,ts] = hs11m(t,x,u,flag)
% Deviation model of the level tank;
% F1*(dx1/dt)+c1*x1+c2*(x1+h1s)^(1/2)-c2*(h1s)^(1/2)=u1 ;
% h1s =1.5 dm, q0s= 0.006359 dm^3/s ;
% c1= 0.00153322 dm^2/s , c2 = 0.00331442 (dm^5/2)/s ;
% F1 = 1.44dm^2, Step change q00s = new value for t>=0;
% u1 is constrained as <-0.006359, 0.004161 dm^3/s>;
136 4 Dynamical Behaviour of Processes
switch flag,
case 0
[sys,x0,str,ts] = mdlInitializeSizes;
case 1,
sys = mdlDerivatives(t,x,u);
case 3,
sys = mdlOutputs(t,x,u);
case 9
sys = [];
end
function [sys,x0,str,ts] = mdlInitializeSizes()
sizes = simsizes;
sizes.NumContStates = 1;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0];
str = [];
ts = [0 0];
function sys = mdlDerivatives(t,x,u)
c1 = 0.00153322;
f1 = 1.44;
a1 = -(c1/f1);
c2 = 0.00331442;
a2 = -(c2/f1);
b1 = 1/f1;
h1s = 1.5;
% Right hand sides;
x1 = x(1)+h1s;
if x1 < 0
x1 = 0;
end
sys(1) = a1*x(1) + a2*sqrt(x1) - a2*sqrt(h1s) + b1*u(1);
function sys = mdlOutputs(t,x,u)
sys = x;
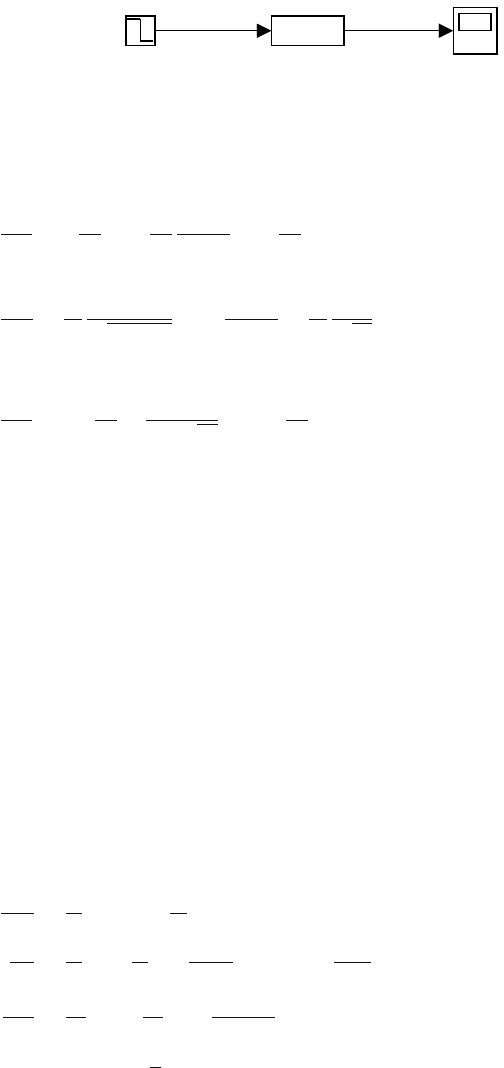
4.2 Computer Simulations 137
hs11m
tank
Step Fcn
Scope
Fig. 4.11. Simulink block scheme for the liquid storage system
Linearised mathematical model in the neighbourhood of the steady-state
x
1
=0is
dx
1
dt
= −
c
1
F
1
x
1
−
1
F
1
∂G(0)
∂x
1
x
1
+
1
F
1
u
1
(4.65)
where
∂G
∂x
1
=
c
2
2
1
x
1
+ h
s
1
,
∂G(0)
∂x
1
=
c
2
2
1
h
s
1
and finally
dx
1
dt
=
−
c
1
F
1
−
c
2
2F
1
h
s
1
x
1
+
1
F
1
u
1
(4.66)
Fig. 4.12 shows the response of the tank to step change of the flow q
0
equal to
−0.0043 dm
3
s
−1
. The steady-state before the change was characterised by the
flow q
s
0
=0.006359 dm
3
s
−1
and the tank level h
s
1
=1.5 dm. The coefficients
c
1
,c
2
and the crossover area F
1
corresponding to the real liquid storage tank
are
c
1
=1.53322.10
−3
dm
2
s
−1
c
2
=3.31142.10
−3
dm
2.5
s
−1
F
1
=1.44dm
2
Fig. 4.12 also shows the step response of the linearised model (4.66). Both
curves can serve for analysis of the error resulting from linearisation of the
mathematical model of the tank.
4.2.5 Time Responses of CSTR
Consider a CSTR with a cooling jacket. In the reactor, an irreversible exother-
mic reaction takes place. We assume that its mathematical model is in the
form
dc
A
dt
=
q
V
c
Av
− c
A
(
q
V
+ k) (4.67)
dϑ
dt
=
q
V
ϑ
v
−
q
V
ϑ −
αF
Vρc
p
(ϑ −ϑ
c
)+
kH
r
ρc
p
c
A
(4.68)
dϑ
c
dt
=
q
c
V
c
ϑ
cv
−
q
c
V
c
ϑ
c
+
αF
V
c
ρ
c
c
pc
(ϑ −ϑ
c
) (4.69)
k = k
0
exp
−
g
ϑ
(4.70)
