Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

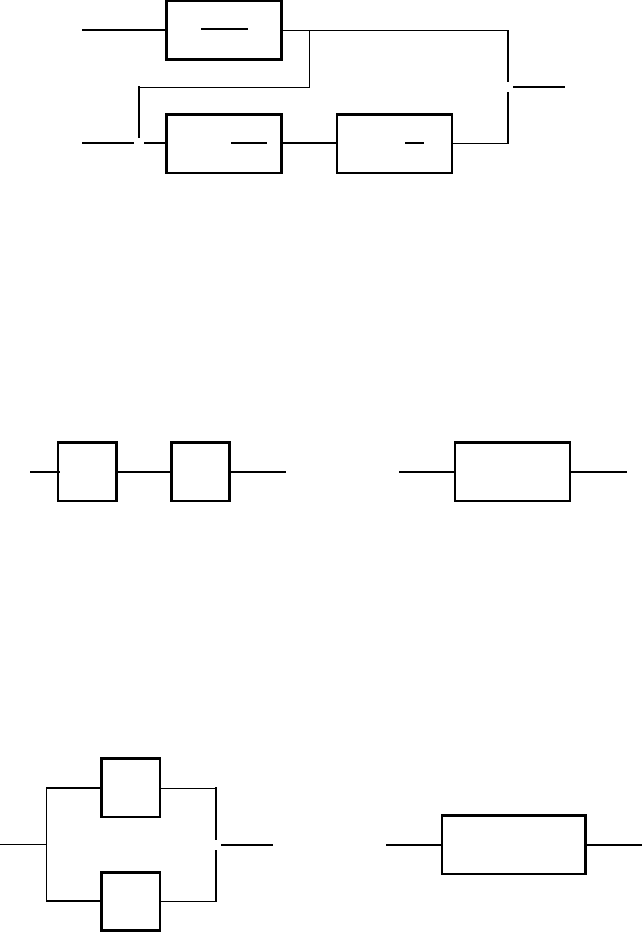
3.3 Input-Output Process Models 97

exp



−



exp



−



s+1

- -

(s)

−

(s)

Fig. 3.17. Block scheme of a double-pipe heat exchanger

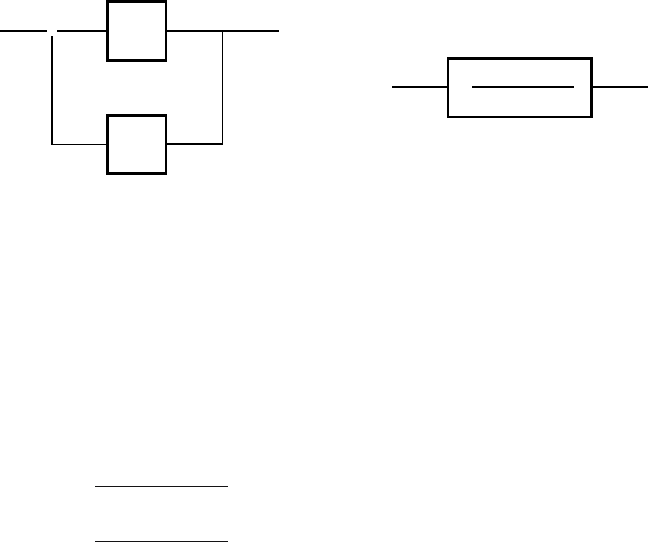
Serial Connection

Serial connection results in a situation when the output variable of the ﬁrst

block is the input variable of the second block (Fig. 3.18). The overall transfer

function can be written as

G(s)=G

(s)G

(s) (3.141)

(s) G

(s)G

(s)

- - - - -

U(s) Y

(s) Y (s)

≡

U(s) Y (s)

Fig. 3.18. Serial connection

Generally when n blocks are connected in series, the transfer function is

given as a product of partial transfer functions:

G(s)=G

(s)G

(s) ...G

(s) (3.142)

Parallel Connection

(s)+G

(s)

- -

≡

U(s) Y (s)

U(s)

(s)

Y (s)

Fig. 3.19. Parallel connection

Parallel connection is characterised by one input variable for all systems.

Output variable is given as the sum of partial outputs (Fig. 3.19). Parallel

connection is characterised by the equations

98 3 Analysis of Process Models

(s)=G

(s)U(s) (3.143)

(s)=G

(s)U(s) (3.144)

Y (s)=Y

(s)+Y

(s) (3.145)

Substituting Y

(s) from (3.143) and Y

(s) from (3.144) into (3.145) yields

Y (s)=[G

(s)+G

(s)]U(s)=G(s)U(s) (3.146)

and

G(s)=G

(s)+G

(s) (3.147)

In general, the overall transfer functions is given as the sum of partial

transfer functions

G(s)=



i=1

(s) (3.148)

Feedback Connection

Feedback connection of two blocks results when output variables of each block

are fed back as the input of the other block (Fig. 3.20).

(s)

1±G

(s)G

(s)

- -

≡

U(s) Y (s)

- -



U(s) E(s) Y (s)

(s)

∓

Fig. 3.20. Feedback connection

For the feedback connection holds

Y (s)=G

(s)E(s) (3.149)

(s)=G

(s)Y (s) (3.150)

E(s)=U(s) ∓ Y

(s) (3.151)

The minus sign in the Eq. (3.151) corresponds to negative feedback and the

plus sign to positive feedback. From these equations follow

(s)=G

(s)G

(s)E(s) (3.152)

E(s)=

1 ±G

(s)G

(s)

U(s) (3.153)

Y (s)=

(s)

1 ±G

(s)G

(s)

U(s)=G(s)U (s) (3.154)

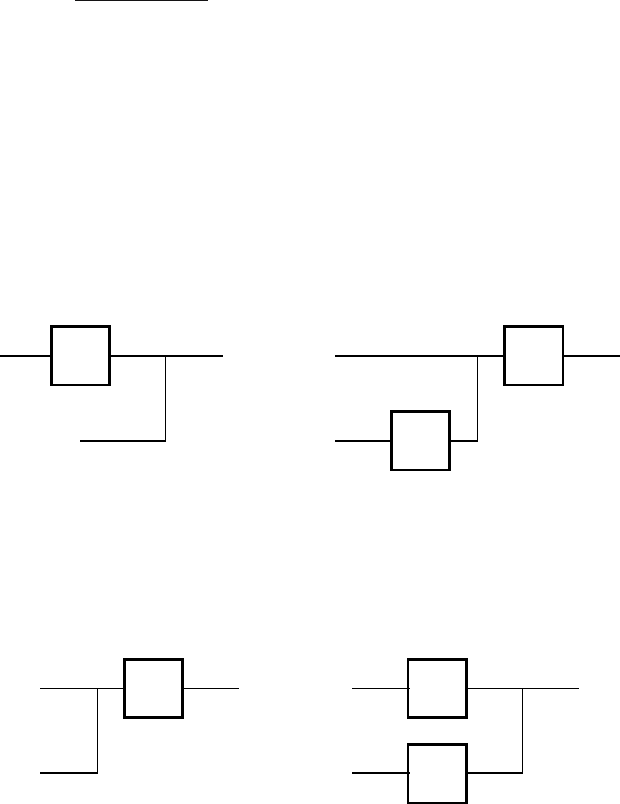
3.3 Input-Output Process Models 99

The overall transfer function is then given as

G(s)=

(s)

1 ±G

(s)G

(s)

(3.155)

The feedback transfer function is a ratio with the numerator given as the

transfer function between the input and output signals and with the denomi-

nator given as a sum (negative feedback) or diﬀerence (positive feedback) of

1 and transfer function of the corresponding open-loop system.

Rule for Moving of the Branching Point

When the branching point is moved against the direction of the previous signal

then the moved branch must contain all blocks which are between the original

and new branching point (Fig. 3.21).

G(s)

- -



- -



≡

Fig. 3.21. Moving of the branching point against the direction of signals

The opposite situation is when the branching point is moved in the direc-

tion of the signal ﬂow. In this case the moved branch contains inverses of the

relevant blocks (Fig. 3.22).

G(s)

−1

(s)

G(s)

- - - -



≡

Fig. 3.22. Moving of the branching point in the direction of signals

Rule for Moving of the Summation Point

Moving of the summation point is an inverse action to moving of the branching

point. The rules are shown in Figs. 3.23 and 3.24.

100 3 Analysis of Process Models

G(s) G(s)

G(s)

- - - - -

≡

Fig. 3.23. Moving of the summation point in the direction of signals

G(s)

−1

(s)

G(s)

- - - - -

≡

Fig. 3.24. Moving of the summation point against the direction of signals

3.3.4 Input Output Models of MIMO Systems - Matrix

of Transfer Functions

The standard and natural description of MIMO systems is in the form of

state-space equations

dx(t)

= Ax(t)+Bu(t) (3.156)

y(t)=Cx(t)+Du(t) (3.157)

where x[n × 1] is the vector of state variables, u[m × 1] is the vector of

input variables, y[r ×1] is the vector of output variables, and A, B, C, D are

constant matrices of appropriate dimensions.

When all variables are deviation variables and x(0) = 0 then the input-

output (I/O) properties of this system can be determined from the convolution

multiplication

y(t)=



g(t −τ )u(τ)dτ (3.158)

where g(t)ismatrix of impulse responses of the [r × m] system and is given

g(t)=



0 t<0

B + Dδ(t) t ≥ 0

(3.159)

and δ(t) is the Dirac delta function.

Consider now the system given by Eqs. (3.156), (3.157). Taking the Laplace

transform yields

3.3 Input-Output Process Models 101

Y (s)=



C(sI −A)

−1

B + D



U(s) (3.160)

Y (s)=G(s)U (s) (3.161)

where

G(s)=C(sI −A)

−1

B + D (3.162)

is [r × m] transfer function matrix of linear continuous system with constant

coeﬃcients. This matrix is the Laplace transform of matrix g(t)

G(s)=



∞

g(t)e

−st

dt (3.163)

The matrix G(s) derived from the original state-space model is the same as

the transfer function matrix of controllable and observable part of this system.

The noncontrollable and nonobservable modes of the system are cancelled in

the process of transformation from state-space models into I/O models. Often,

there are tasks of the inverse transformation from I/O to state-space (SS)

model. It must be emphasised that one I/O model corresponds to an inﬁnite

number of state-space models. We then speak about a state-space realisation

of I/O model. Minimum realisation fulﬁls the properties of controllability and

observability. Hence an unambiguous relation between G(s) and its state-

space realisation exists only if the state-space model is minimal.

If we deal with SISO systems we can write

G(s)=C(sI −A)

−1

B + D =

B(s)

A(s)

(3.164)

If the state-space model is the minimal realisation of G(s) then

det(sI −A)=A(s) (3.165)

The degree of characteristic polynomial A(s) is equal to n where n is the

number of states of state-space model. We call n as system order.

Any transfer function can be one of the following forms:

G(s)=

+ b

m−1

+ ···+ b

+ a

n−1

+ ···+ a

,n≥ m (3.166)

G(s)=

(s −s

)(s −s

) ...(s −s

)

(s −s

)(s −s

) ...(s −s

)

(3.167)

Roots of the characteristic polynomial s

,...,s

are system poles. Roots

of numerator polynomial s

,...,s

are system zeros.

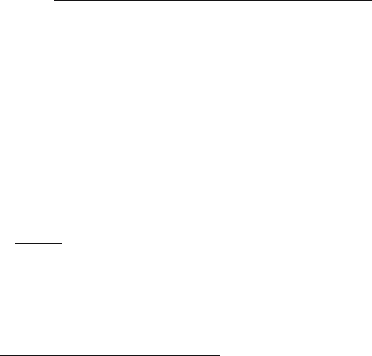
102 3 Analysis of Process Models

G(s)=Z

s + 1)(T

s +1)...(T

s +1)

s + 1)(T

s +1)...(T

s +1)

(3.168)

where T

,...,T

are time constants and Z

= b

is the

system gain. This expression for transfer function can only be written if all

poles and zeros are real. Time constants correspond to negative inverses

of poles and zeros.

Transfer function matrix G(s) has dimensions [r ×m]. An element of this

matrix G

(s) is the transfer function corresponding to input u

and output y

(s)=

(s)

(3.169)

The matrix G(s) can also be written as

G(s)=

Cadj(sI −A)B + Dd(s)

d(s)

(3.170)

where d(s)=|sI − A|.

As all elements of adj(sI −A) are polynomials with a degree less than or

equal to n − 1 and polynomial d(s) is of degree n then all transfer functions

(s) have a degree of numerator less than or equal to the degree of the

denominator. G(s)isproper rational function matrix. When D = 0 then all

numerator degrees are less than the denominator degrees and G(s)isstrictly

proper rational function matrix.

Deﬁnition of proper and strictly proper transfer function matrix G(s):

A rational matrix G(s)[r × m] is proper if all its transfer functions satisfy

lim

|s|→∞

(s) < ∞. A rational matrix G(s) is strictly proper if for all its

elements hold lim

|s|→∞

(s) = 0. The numerator degree of a proper SISO

system is smaller or equal to the denominator degree. The numerator degree

of a strictly proper SISO system is smaller as the denominator degree.

Roots of polynomial d(s) are poles of G(s). If no cancellation of roots

occurs during the calculation of G(s) then the matrix poles are the same as

system poles.

If all poles of G(s) are located in the left half plane of the complex plane

then the frequency transfer function matrix that is deﬁned as Fourier trans-

formation of g(t) exists and can be obtained by the substitution s =jω, i.e.

G(jω)=C(jωI − A)

−1

B + D (3.171)

The Fourier transform is deﬁned as

F (jω) ≡



∞

−∞

f(t)e

−jωt

dt (3.172)

3.3 Input-Output Process Models 103

G(jω) is called the frequency transfer function matrix. The values of G(jω)

are for any real ω given as values of G(s)fors =jω.

G(jω)= G(s)|

s=jω

(3.173)

This function can be introduced not only for stable but for arbitrary transfer

functions. However, if G(s) has a root on imaginary axis s

=jβ

then G(jω)

has an inﬁnite value for ω = β

Example 3.16: CSTR - transfer function matrix

Consider the CSTR shown in Fig. 2.11 and assume the same notation as

in the Example 3.14. The state-space model matrices are

A =





, B =



0 b



, C = I

From (3.162) follows

G(s) = I



−





−1



0 b





s −a

−a

s −a



−1



0 b



(s −a

)(s −a

) −a



s −a



0 b



(s −a

)(s −a

) −a



s −a



The partial transfer functions of G(s) are the same as in the example 3.14.

3.3.5 BIBO Stability

BIBO stability plays an important role among diﬀerent deﬁnitions of stability.

The abbreviation stands for Bounded Input, Bounded Output. Roughly said,

a system is BIBO stable if any bounded input gives a bounded output. This is

also the reason why we sometimes speak about BIBO stability as of external

stability.

Deﬁnition of BIBO stability: A linear continuous system with constant

coeﬃcients (3.156), (3.157) with zero initial state x(t

) is BIBO stable if for

all t

and for all inputs u(t) that are ﬁnite on [t

, ∞) is output y(t) also ﬁnite

on [t

, ∞).

Theorem: BIBO stability. A linear continuous system with constant coef-

ﬁcients (3.156), (3.157) is BIBO stable if and only if



∞

g(τ)dτ<∞ (3.174)

104 3 Analysis of Process Models

where the norm is induced by the norm on u.

An alternate theorem about BIBO stability states: A linear continuous

system with constant coeﬃcients (3.156), (3.157) is BIBO stable if and only

if all poles of transfer function matrix G(s) lie in the open left half plane of

the complex plane.

Asymptotic stability of linear continuous systems with constant coeﬃcients

implies BIBO stability but the opposite case need not be true.

3.3.6 Transformation of I/O Models into State-Space Models

In the previous sections we found out that an input-output model can be

transformed into inﬁnitely many state-space models. In this section we show

the procedures of this transformation that lead to controllable and observable

canonical forms for SISO systems.

Controllable Canonical Form

Consider a system with transfer function in the form

G(s)=

+ b

m−1

+ ···+ b

s + b

+ a

n−1

+ ···+ a

s + a

,n≥ m (3.175)

Let us introduce an auxiliary variable z(t) and its Laplace transform Z(s)

such that

Y (s)

Z(s)

= b

+ b

m−1

+ ···+ b

s + b

(3.176)

Z(s)

U(s)

+ a

n−1

+ ···+ a

s + a

(3.177)

Equation (3.177) corresponds to the following diﬀerential equation

z(t)

+ a

n−1

z(t)

n−1

+ ···+ a

˙z(t)+a

z(t)=u(t) (3.178)

Now let us deﬁne state variables by the following relations

z(t)

= x

i+1

(t),i=0, 1,...,n− 1 (3.179)

(t)

= x

i+1

(t),i=1, 2,...,n− 1 (3.180)

(3.181)

Equation (3.178) can now be transformed into n ﬁrst order diﬀerential

equations

3.3 Input-Output Process Models 105

(t)

= x

(t)

= x

(t)

. (3.182)

n−1

(t)

= x

(t)

z(t)

= −a

n−1

−···−a

(t) −a

(t)+u(t)

When n = m then Eq. (3.176) corresponds to

y(t)=b

(t)+b

(t)+···+ b

n−1

(t)+b

˙x

(t) (3.183)

˙x

(t) from this equation can be obtained from Eq. (3.182) and yields

y(t)=(b

− a

(t)+(b

− a

(t)+···+

+(b

n−1

− a

n−1

(t)+b

u(t) (3.184)

Equations (3.182) and (3.184) form a general state-space model of the form

dx(t)

= A

x(t)+B

u(t) (3.185)

y(t)=C

x(t)+D

u(t) (3.186)

where x =(x

,...,x

)

⎛

⎜

⎝

010... 0

001... 0

000... 1

−a

... −a

n−1

⎞

⎟

⎠

, B

⎛

⎜

⎝

⎞

⎟

⎠



− a

... b

n−1

− a

n−1



, D

= b

We see that if m<nthen D = 0. This system of state-space equations can be

shown to be always controllable but it need not be observable. We speak about

controllable canonical form of a system. The corresponding block scheme is

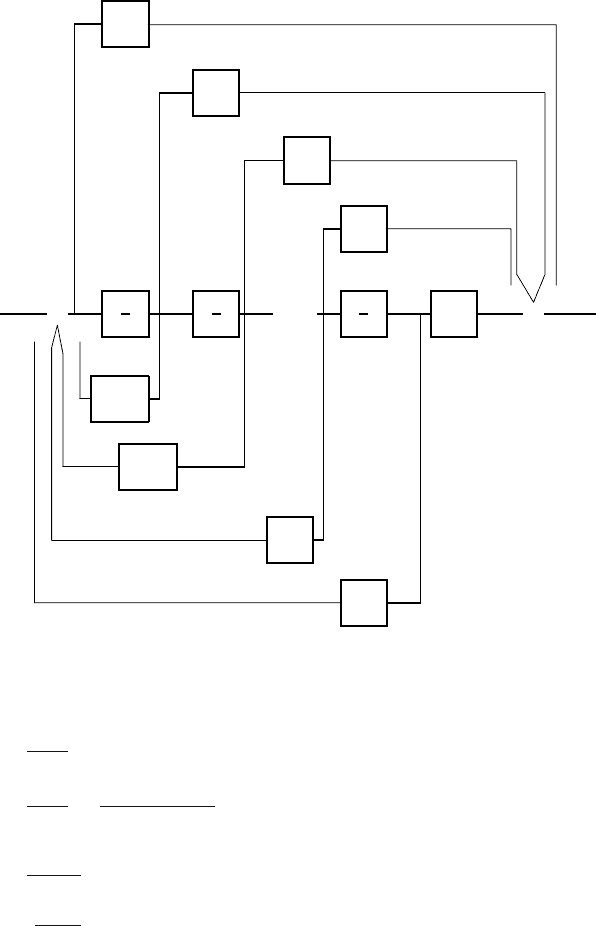
shown in Fig. 3.25.

Example 3.17: Controllable canonical form of a second order system

Consider a system described by the following diﬀerential equation

¨y(t)+a

˙y(t)+a

y(t)=b

˙u(t)+b

u(t)

and corresponding transfer function

Y (s)

U(s)

s + b

+ a

s + a

106 3 Analysis of Process Models

−a

n−1

n−2

jj- - - - - - - -



>



=

−a

n−1

−a

n−2

−a



...

u(t)

˙x

n−1

y(t)

Fig. 3.25. Block scheme of controllable canonical form of a system

We introduce Z(s) such the following equations hold

Y (s)

Z(s)

= b

s + b

Z(s)

U(s)

+ a

s + a

State-space equations can be written as

(t)

= x

(t)

= −a

(t) −a

(t)+u(t)

y(t)=b

(t)+b

(t)

and the corresponding block scheme is shown in Fig. 3.26.