Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


3.3 Input-Output Process Models 87
where
f
1
(h
1
,q
0
)=−
k
11
F
1
h
1
+
1
F
1
q
0
For the steady-state follows
0=−
k
11
F
1
h
s
1
+
1
F
1
q
s
0
q
s
1
= k
11
h
s
1
Linearised dynamical properties in the neighbourhood of the steady-state
are of the form
dh
1
dt
=
d(h
1
− h
s
1
)
dt
= −
k
11
2F
1
h
s
1
(h
1
− h
s
1
)+
1
F
1
(q
0
− q
s
0
)
and linearised output equation is
q
1
− q
s
1
=
k
11
2
h
s
1
(h
1
− h
s
1
)
Let us introduce deviation variables
x
1
= h
1
− h
s
1
u = q
0
− q
s
0
y
1
= q
1
− q
s
1
Linear state-space model of the first tank is
dx
1
dt
= a
11
x
1
+ b
11
u
y
1
= c
11
x
1
where
a
11
= −
k
11
2F
1
h
s
1
,b
11
=
1
F
1
,c
11
=
k
11
2
h
s
1
.
After applying the Laplace transform to these equations and using the
fact that initial conditions are zero we obtain
sX
1
(s)=a
11
X
1
(s)+b
11
U(s)
Y (s)=c
11
X
1
(s)
or
(s −a
11
)Y (s)=c
11
b
11
U(s)
The first tank transfer function G
1
(s)is
G
1
(s)=
Y
1
(s)
U(s)
=
1
a
1
s +1
=
1
T
1
s +1
where a
1
= T
1
=(2F
h
s
1
)/k
11
and the gain is equal to one.
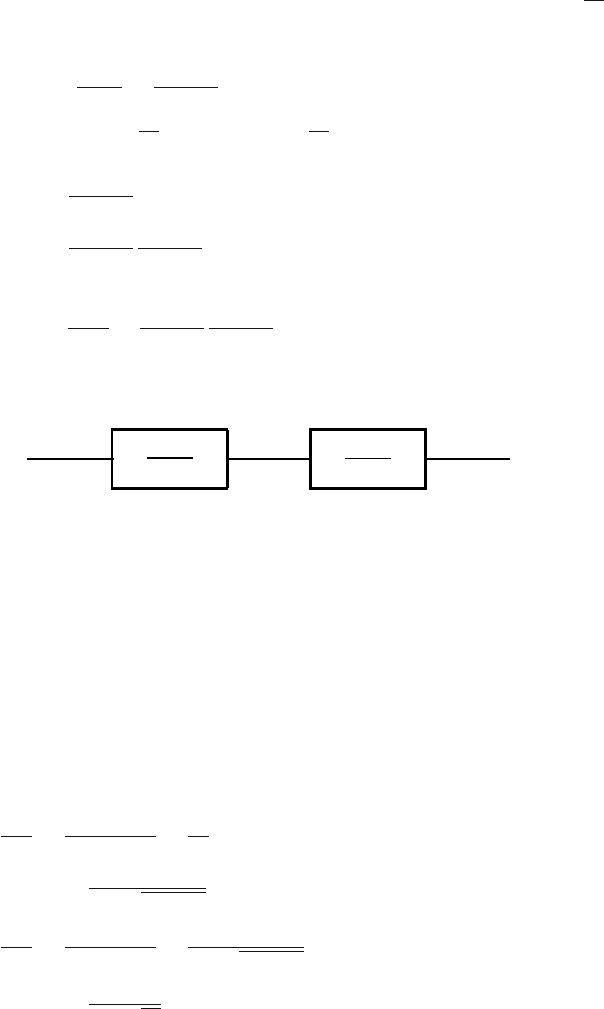
88 3 Analysis of Process Models
The transfer function of the second tank G
2
(s) can be derived when con-
sidering deviation variables x
2
= y = h
2
−h
s
2
and the relation q
2
= k
22
√
h
2
and is given as
G
2
(s)=
Y (s)
Y
1
(s)
=
Z
2
T
2
s +1
where T
2
=(2F
2
h
s
2
)/k
22
, Z
2
=(2
h
s
2
)/k
22
. The output Y (s)canbe
written as
Y (s)=
Z
2
T
2
s +1
Y
1
(s)
Y (s)=
Z
2
T
2
s +1
1
T
1
s +1
U(s)
The overall transfer function of both tanks in a series is then
G(s)=
Y (s)
U(s)
=
Z
2
T
2
s +1
1
T
1
s +1
Block scheme of this system is shown in Fig. 3.11.
1
T
1
s+1
Z
2
T
2
s+1
- -
U(s) Y
1
(s)
-
Y (s)
Fig. 3.11. Block scheme of two tanks in a series
Note 3.3. The example given above shows serial connection of two systems
where the second system does not influence the behaviour of the first
system. We can speak about “one-way” effect.
When the systems influence each other, the overall transfer function can-
not be obtained as a product of transfer functions of subsystems. This
is shown in the next example dealing with the interacting two tanks in
a series (See Fig. 2.2). Mathematical model of this system described by
equations (2.21) and (2.22) can be linearised in the neighbourhood of the
steady-state given by flow rate q
s
0
and levels h
s
1
,h
s
2
as
dh
1
dt
=
d(h
1
− h
s
1
)
dt
=
1
F
1
(q
0
− q
s
0
)
−
k
11
2F
1
h
s
1
− h
s
2
[(h
1
− h
s
1
) −(h
2
− h
s
2
)]
dh
2
dt
=
d(h
2
− h
s
2
)
dt
=
k
11
2F
2
h
s
1
− h
s
2
[(h
1
− h
s
1
) −(h
2
− h
s
2
)]
−
k
22
2F
2
h
s
2
(h
2
− h
s
2
)
Introducing deviation variables

3.3 Input-Output Process Models 89
x
1
= h
1
− h
s
1
,u= q
0
− q
s
0
,y= x
2
= h
2
− h
s
2
yields the linear model
dx
1
dt
= a
11
x
1
+ a
12
x
2
+ b
11
u
dx
2
dt
= a
21
x
1
+ a
22
x
2
y = x
2
where
a
11
= −
k
11
2F
1
h
s
1
− h
s
2
,a
12
= −a
11
,b
11
=
1
F
1
a
21
= −
k
11
2F
2
h
s
1
− h
s
2
,a
22
= −a
21
−
k
22
2F
2
h
s
2
,
Taking the Laplace transform yields
sX
1
(s)=a
11
X
1
(s)+a
12
X
2
(s)+b
11
U(s)
sX
2
(s)=a
21
X
1
(s)+a
22
X
2
(s)
Y (s)=X
2
(s)
or
(s
2
− (a
11
+ a
22
)s +(a
11
a
22
− a
12
a
21
))Y (s)=a
21
b
11
U(s)
and hence the transfer function is given as
G(s)=
Y (s)
U(s)
=
b
0
a
2
s
2
+ a
1
s +1
where
b
0
=
a
21
b
11
a
11
a
22
− a
12
a
21
a
2
=
1
a
11
a
22
− a
12
a
21
a
1
= −
a
11
+ a
22
a
11
a
22
− a
12
a
21
Example 3.11: n tanks in a series - transfer function
Assume n tanks in a series as shown in Fig. 3.12 and the corresponding
block scheme in Fig. 3.13. The variable U(s) denotes the Laplace transform
of u(t)=q
0
(t) − q
s
0
, Y
i
(s) are the Laplace transforms of y
i
(t)=q
i
(t) −
q
s
0
,i=1...n− 1, Y (s) is the Laplace transform of y(t)=h
n
(t) − h
s
n
.
T
1
,T
2
,...,T
n
are time constants and Z
n
is gain.
Similarly as in the case of the two tanks without interaction, the partial
input and output variables are tied up with the following relations
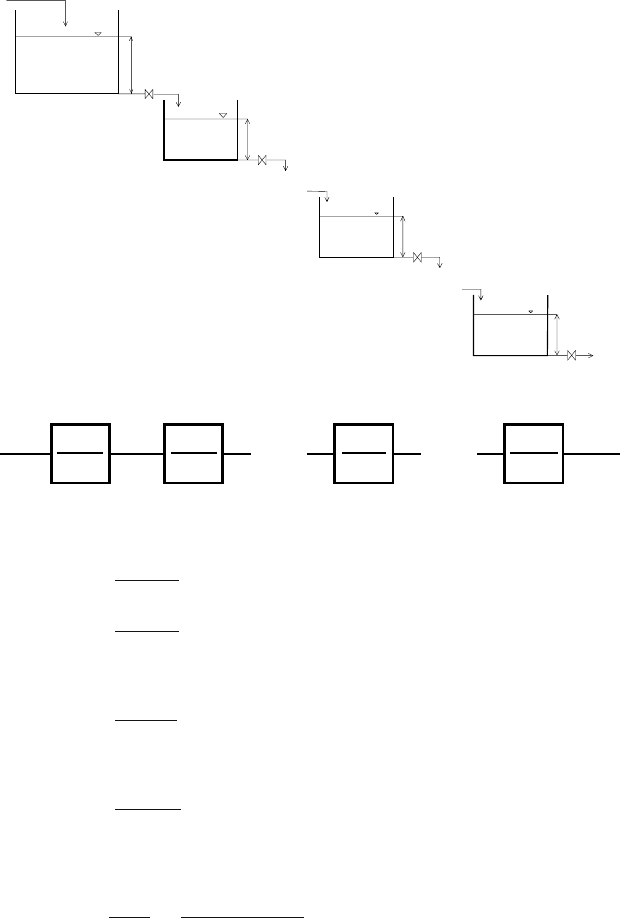
90 3 Analysis of Process Models
q
0
h
h
1
2
h
i
h
n
q
i
q
n-1
q
n
. . . . . .
. . . . . .
q
i-1
q
1
q
2
Fig. 3.12. Serial connection of n tanks
1
T
1
s+1
1
T
2
s+1
1
T
i
s+1
Z
n
T
n
s+1
- - - - - - -
... ...
U(s) Y
1
(s) Y
i−1
(s)
Y
i
(s)
Y
n−1
(s) Y (s)
Fig. 3.13. Block scheme of n tanks in a series
Y
1
(s)=
1
T
1
s +1
U(s)
Y
2
(s)=
1
T
2
s +1
Y
1
(s)
.
.
.
Y
i
(s)=
1
T
i
s +1
Y
i−1
(s)
.
.
.
Y (s)=
Z
n
T
n
s +1
Y
n−1
(s)
The overall input variable is U (s) and the overall output variable is Y (s).
The overall transfer function is then
G(s)=
Y (s)
U(s)
=
Z
n
+
n
i=1
(T
i
s +1)
Simplified block scheme of this system is shown in Fig. 3.14.
Example 3.12: U-tube : transfer function
Mathematical model of the U-tube shown in Fig. 3.5 is of the form

3.3 Input-Output Process Models 91
Z
n
+
n
i=1
(T
i
s+1)
- -
U(s) Y (s)
Fig. 3.14. Simplified block scheme of n tanks in a series
L
2g
d
2
h
dt
2
+
k
2gρ
dh
dt
+ h =
1
2gρ
p
v
Steady-state is determined by level of liquid h = h
s
= 0. We denote the
output deviation variable as y = h and the input deviation variable as
u = h
v
= p
v
/2gρ. Further let us introduce 1/ω
2
k
= L/2g,2ζ/ω
k
= k/2gρ
where ω
k
is a critical frequency and ζ is a damping coefficient. The terms
critical frequency and damping coefficient will become clear from analysis
of the solution of the differential equation describing dynamical properties
of the U-tube. Mathematical model can be then rewritten as
1
ω
2
k
d
2
y
dt
2
+2
ζ
ω
k
dy
dt
+ y = u
and the corresponding transfer function as
G(s)=
Y (s)
U(s)
=
1
T
2
k
s
2
+2ζT
k
s +1
where T
k
=1/ω
k
.
Note 3.4. Mathematical model of the U-tube shows that step function on input
can result in an oscillatory response. Therefore, U-tube is able of to produce
its own oscillations. This is in contrast to other systems of the second order
that can be decomposed into two systems of the first order and cannot produce
the oscillations.
Example 3.13: Heat exchanger - transfer function
Mathematical model of a heat exchanger was developed in the Section 2.2
andwasshowntobeintheform
T
1
dy
1
dt
+ y
1
= Z
1
u
1
+ Z
2
r
1
where y
1
= ϑ = ϑ
s
,u
1
= ϑ
p
− ϑ
s
p
, r
1
= ϑ
v
− ϑ
s
v
and T
1
,T
2
,Z
2
are
constants. The output variable is the natural state variable y
1
= x
1
.
To determine the heat exchanger response to the change of inlet temper-
ature ϑ
v
it is necessary to set u
1
= 0 and analogously if response of the
process to the jacket temperature change is desired then r
1
= 0. The vari-
able u
1
is usually assumed to be a manipulated variable and r
1
acts as a
disturbance.
Taking the Laplace transform and considering zero initial conditions yields
92 3 Analysis of Process Models
(T
1
s +1)Y
1
(s)=Z
1
U
1
(s)+Z
2
R
1
(s)
if R
1
(s) = 0 then
G
1
(s)=
Y
1
(s)
U
1
(s)
=
Z
1
T
1
s +1
if U
1
(s) = 0 then
G
2
(s)=
Y
1
(s)
R
1
(s)
=
Z
2
T
1
s +1
Y
1
(s) can be written as
Y
1
(s)=
Z
1
T
1
s +1
U
1
(s)+
Z
2
T
1
s +1
R
1
(s)
Y
1
(s)=G
1
(s)U
1
(s)+G
2
(s)R
1
(s)
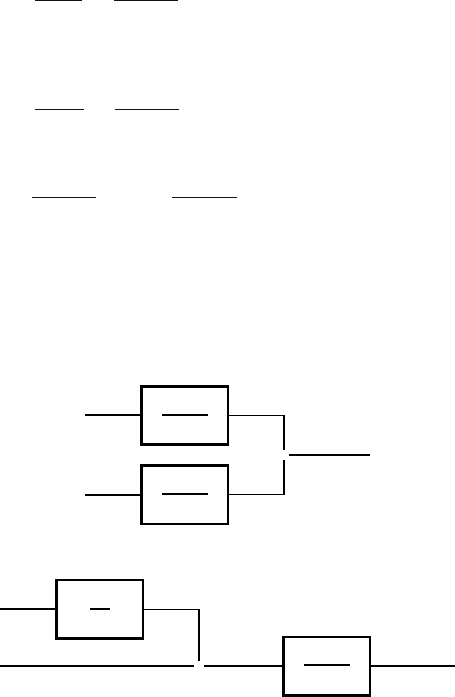
Block scheme of this process is shown in Fig. 3.15 or in Fig. 3.16 where r
1
is moved from output to input to the system. This has an importance in
design of control systems because modified block scheme simplifies some
considerations.
Z
1
T
1
s+1
Z
2
T
1
s+1
-
-
e
?
6
-
R
1
(s)
U
1
(s)
Y
1
(s)
Fig. 3.15. Block scheme of a heat exchanger
Z
2
Z
1
Z
1
T
1
s+1
e
-
?
- --
R
1
(s)
U
1
(s) Y
1
(s)
Fig. 3.16. Modified block scheme of a heat exchanger
Example 3.14: CSTR - transfer function
Consider the CSTR shown in Fig. 2.11. Let us introduce deviation vari-
ables
y
1
= x
1
= c
A
− c
s
A
y
2
= x
2
= ϑ − ϑ
s
u
1
= c
Av
− c
s
Av
u
2
= ϑ
c
− ϑ
s
c

3.3 Input-Output Process Models 93
The linearised mathematical model is then of the form
dx
1
dt
= a
11
x
1
+ a
12
x
2
+ b
11
u
1
dx
2
dt
= a
21
x
1
+ a
22
x
2
+ b
22
u
2
Compared to the Example 2.6, b
11
= h
11
,b
22
= b
21
and inlet temperature
is assumed to be constant. We define the following transfer functions
G
11
(s)=
Y
1
(s)
U
1
(s)
G
12
(s)=
Y
1
(s)
U
2
(s)
G
21
(s)=
Y
2
(s)
U
1
(s)
G
22
(s)=
Y
2
(s)
U
2
(s)
Taking the Laplace transform of linearised mathematical model follows
sX
1
(s)=a
11
X
1
(s)+a
12
X
2
(s)+b
11
U
1
(s)
sX
2
(s)=a
21
X
1
(s)+a
22
X
2
(s)+b
22
U
2
(s)
The transfer function G
11
(s) can be derived if U
2
(s) = 0. Analogously,
other transfer functions can also be obtained.
G
11
(s)=
b
11
s −a
22
b
11
s
2
− (a
11
+ a
22
)s +(a
11
a
22
− a
12
a
21
)
G
12
(s)=
a
12
b
22
s
2
− (a
11
+ a
22
)s +(a
11
a
22
− a
12
a
21
)
G
21
(s)=
a
21
b
11
s
2
− (a
11
+ a
22
)s +(a
11
a
22
− a
12
a
21
)
G
22
(s)=
b
22
s −a
11
b
22
s
2
− (a
11
+ a
22
)s +(a
11
a
22
− a
12
a
21
)
3.3.2 Transfer Functions of Systems with Time Delays
Consider a process described by the differential equation
∂x
1
(σ, t)
∂t
+ v
σ
∂x
1
(σ, t)
∂σ
=0,x
1
(σ, 0) = 0 (3.123)
This equation is a description of a mathematical model of the double pipe heat
exchanger shown in Fig. 2.5 with α =0andx
1
being deviation temperature
in the inner pipe. The process input variable is
u(t)=x
1
(0,t)=x
0
1
(t) (3.124)
and the output variable is defined as
y(t)=x
1
(L, t) (3.125)
The system defined with the above equations is called pure time delay.
After taking the Laplace transform with argument t we get
v
σ
∂X
1
(σ, s)
∂σ
+ sX
1
(σ, s) = 0 (3.126)

94 3 Analysis of Process Models
where
X
1
(σ, s)=
∞
0
x
1
(σ, t)e
−st
dt (3.127)
Applying the Laplace transform with argument σ yields
v
σ
q
¯
X
1
(q, s) −v
σ
U(s)+s
¯
X
1
(q, s) = 0 (3.128)
where
¯
X
1
(q, s)=
∞
0
X
1
(σ, s)e
−qσ
dσ (3.129)
U(s)=X
1
(0,s) (3.130)
From Eq. (3.128) follows
¯
X
1
(q, s)=
1
q +
s
v
σ
U(s) (3.131)
This equation can be transformed back into σ domain
X
1
(σ, s)=e
−
σ
v
σ
s
U(s) (3.132)
The corresponding transfer function of pure time delay for any σ ∈ [0,L]is
G
dσ
=
X
1
(σ, s)
U(s)
=e
−
σ
v
σ
s
(3.133)
and for σ = L
G
d
=
Y (s)
U(s)
=e
−T
d
s
(3.134)
where T
d
= L/v
σ
.
Let us now consider only part of the process of length Δσ that is perfectly
mixed. The equation (3.123) can be approximated as
dx
1
(Δσ, t)
dt
= v
σ
−x
1
(Δσ, t)+u(t)
Δσ
(3.135)
This equation after taking the Laplace transform is of the form
X
1
(Δσ, t)
U(s)
=
1
1+
Δσ
v
σ
s
(3.136)
Because the term e
Δσ
v
σ
s
can be written as
1
e
Δσ
v
σ
s
=
1
1+
Δσ
v
σ
s +
1
2
Δσ
2
v
2
σ
s
2
+ ···
(3.137)

3.3 Input-Output Process Models 95
then the right hand side term of (3.136) can be viewed as the first order
approximation of time delay term.
Let us further assume mass balance of the process of length Δσ of the
form
d
dt
u(t)+x
1
(Δσ, t)
2
= v
σ
−x
1
(Δσ, t)+u(t)
Δσ
(3.138)
Taking the Laplace transform becomes
X
1
(Δσ, t)
U(s)
=
1 −
1
2
Δσ
v
σ
s
1+
1
2
Δσ
v
σ
s
(3.139)
This equation can be understood as the first order Pade approximation of
time delay term. Similarly for the second order Pade approximation yields
X
1
(Δσ, t)
U(s)
=
1 −
1
2
Δσ
v
σ
s +
1
12
Δσ
2
v
2
σ
s
2
1+
1
2
Δσ
v
σ
s +
1
12
Δσ
2
v
2
σ
s
2
(3.140)
Example 3.15: Double-pipe heat exchanger - transfer functions
Consider the heat exchanger shown in Fig. 2.5. It can be described by the
following differential equation
T
1
∂ϑ(σ, t)
∂t
+ v
σ
T
1
∂ϑ(σ, t)
∂σ
+ ϑ(σ, t)=ϑ
p
(t)
Assume boundary and initial conditions of the form
ϑ(0,t)=ϑ
0
(t)
ϑ(σ, 0) = ϑ
s
(σ)=ϑ
s
p
− (ϑ
s
p
− ϑ
0s
p
)e
−
σ
v
σ
T
1
ϑ
p
(t)=ϑ
s
p
,t<0
ϑ
0
(t)=ϑ
0s
,t<0
and deviation variables
x
1
(σ, t)=ϑ(σ, t) −ϑ
s
(σ)
u
1
(t)=ϑ
p
(t) −ϑ
s
p
u
2
(t)=ϑ
0
(t) −ϑ
0s
The differential equation of the heat exchanger then becomes
T
1
∂x
1
(σ, t)
∂t
+ v
σ
T
1
∂x
1
(σ, t)
∂σ
+ x
1
(σ, t)=u
1
(t)
with boundary and initial conditions
x
1
(0,t)=u
2
(t)
x
1
(σ, 0) = 0
u
1
(t)=0,t<0
u
2
(t)=0,t<0

96 3 Analysis of Process Models
Taking the Laplace transform with an argument t yields
(T
1
s +1)X
1
(σ, s)+v
σ
T
1
∂X
1
(σ, s)
∂σ
= U
1
(s)
where
X
1
(σ, s)=
∞
0
x
1
(σ, t)e
−st
dt
The second Laplace transform gives
(T
1
s + v
σ
T
1
q +1)
¯
X
1
(q, s)=
1
q
U
1
(s)+v
σ
T
1
U
2
(s)
where
¯
X
1
(q, s)=
∞
0
X
1
(σ, s)e
−qσ
dσ
U
2
(s)=X
1
(0,s)
¯
X
1
(q, s) can be written as
¯
X
1
(q, s)=
1
T
1
s +1
a
q(q + a)
U
1
(s)+
1
q + a
U
2
(s)
where a =(T
1
s +1)/v
σ
T
1
.
The inverse Laplace transform according to σ gives
X
1
(σ, s)=
1
T
1
s +1
1 −e
−
T
1
s+1
v
σ
T
1
σ
U
1
(s)+e
−
T
1
s+1
v
σ
T
1
σ
U
2
(s)
which shows that the transfer functions are of the form
G
1k
=
Y
k
(s)
U
1
(s)
=
1
T
1
s +1
1 −e
−
σ
k
v
σ
T
1
e
−
σ
k
v
σ
s
G
2k
=
Y
k
(s)
U
2
(s)
=e
−
σ
k
v
σ
T
1
e
−
σ
k
v
σ
s
where
Y
k
(s)=X
1
(σ
k
,s),k=1, 2,...,r;0≤ σ
k
≤ L
Block scheme of the double-pipe heat exchanger is shown in Fig. 3.17.
3.3.3 Algebra of Transfer Functions for SISO Systems
Investigation of block schemes reveals the fact that all schemes can be decom-
posed into 3 basic connections: serial, parallel, and feedback. The rules that
enable to determine the overall transfer function of a system composed from
basic blocks are called algebra of transfer functions.
