Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

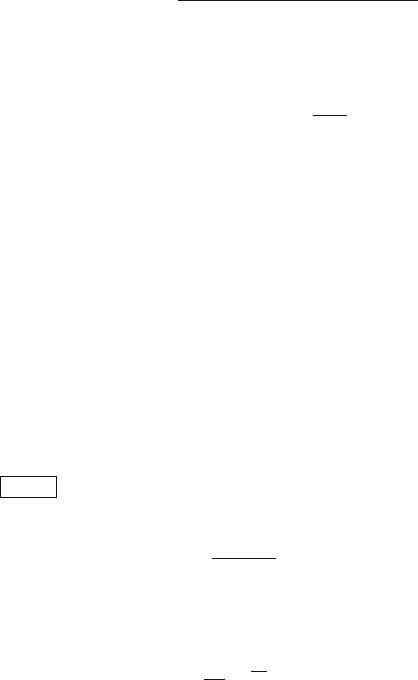
118 4 Dynamical Behaviour of Processes

x(t)=e

x(0) +



A(t−τ)

Bu(τ )dτ (4.4)

y(t)=Cx(t)+Du(t) (4.5)

and replace u(t) with δ(t)weget

x(t)=e

x(0) + e

B (4.6)

y(t)=Ce

x(0) + Ce

B + Dδ(t) (4.7)

For x(0) = 0 then follows

y(t)=Ce

B + Dδ(t)=g(t) (4.8)

Consider the transfer function G(s)oftheform

G(s)=

+ b

n−1

+ ···+ b

+ a

n−1

+ ···+ a

(4.9)

The initial value theorem gives

g(0) = lim

s→∞

sG(s)=

⎧

⎨

⎩

∞, if b

=0

n−1

, if b

0, if b

= b

n−1

(4.10)

and g(t)=0fort<0.

If for the impulse response holds g(t)=0fort<0 then we speak about

causal system.

From the Duhamel integral

y(t)=



g(t −τ )u(τ)dτ (4.11)

follows that if the condition



|g(t)|dt<∞ (4.12)

holds then any bounded input to the system results in bounded system output.

Example 4.1: Impulse response of the ﬁrst order system

www

Assume a system with transfer function

G(s)=

s +1

then the corresponding weighting function is the inverse Laplace transform

of G(s)

g(t)=

−

The graphical representation of this function is shown in Fig. 4.1.

4.1 Time Responses of Linear Systems to Unit Impulse and Unit Step 119

0 1 2 3 4 5 6

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

t / T

Fig. 4.1. Impulse response of the ﬁrst order system

4.1.2 Unit Step Response

Step response is a response of a system with zero initial conditions to the unit

step function 1(t). Consider a system with transfer function G(s) for which

holds

Y (s)=G(s)U(s) (4.13)

If the system input variable u(t) is the unit step function

u(t)=1(t) (4.14)

then the system response (for zero initial conditions) is

y(t)=L

−1



G(s)



(4.15)

From this equation it is clear that step response is a time counterpart of the

term G(s)/s or equivalently G(s)/s is the Laplace transform of step response.

The impulse response is the time derivative of the step response.

Consider again the state-space approach. For u(t)=1(t) we get from (3.47)

x(t)=e

x(0) +



A(t−τ)

Bu(t)dτ (4.16)

x(t)=e

x(0) + e

(−A

−1

)(e

−At

− I)B (4.17)

x(t)=e

x(0) + (e

− I)A

−1

B (4.18)

y(t)=Ce

x(0) + C(e

− I)A

−1

B + D (4.19)

For x(0) = 0 holds

y(t)=C(e

− I)A

−1

B + D (4.20)

120 4 Dynamical Behaviour of Processes

If all eigenvalues of A have negative real parts, the steady-state value of

step response is equal to G(0). This follows from the Final value theorem (see

page 58)

lim

t→∞

y(t) = lim

s=0

G(s)=−CA

−1

B + D =

(4.21)

The term b

is called (steady-state) gain of the system.

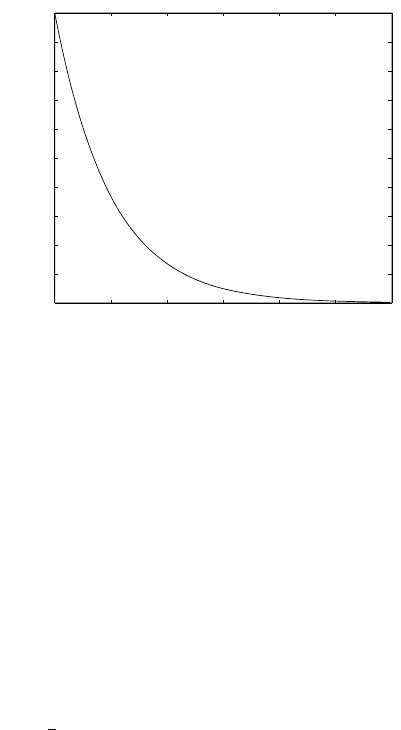
Example 4.2: Step response of ﬁrst order system

www

Assume a process that can be described as

+ y = Z

This is an example of the ﬁrst order system with the transfer function

G(s)=

s +1

The corresponding step response is given as

y(t)=Z

(1 −e

−

)

the gain and T

time constant of this system. Step response of this

system is shown in Fig 4.2.

0 2 4 6 8

0.2

0.4

0.6

0.8

1.2

y / Z

Fig. 4.2. Step response of a ﬁrst order system

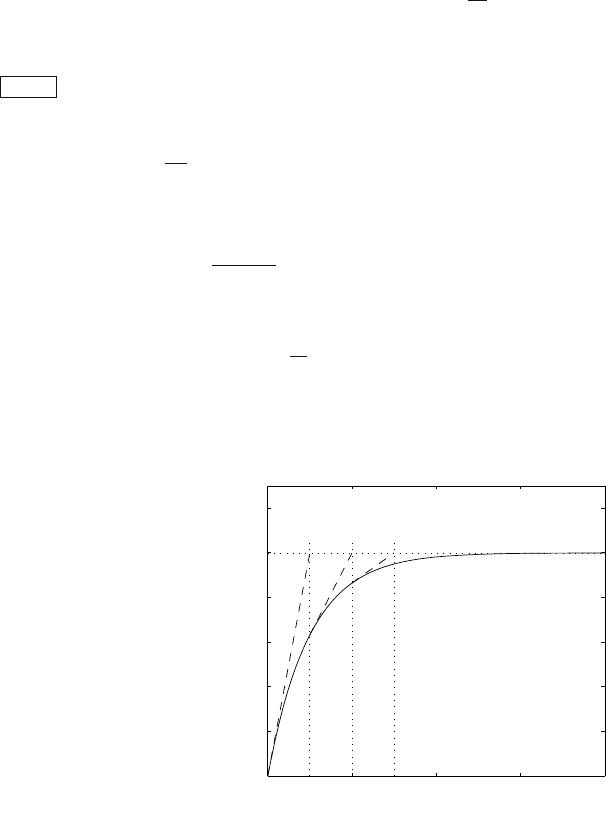
Step responses of the ﬁrst order system with various time constants are

shown in Fig 4.3. The relation between time constants is T

4.1 Time Responses of Linear Systems to Unit Impulse and Unit Step 121

0 5 10 15

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

y / Z

Fig. 4.3. Step responses of a ﬁrst order system with time constants T

Example 4.3: Step responses of higher order systemswww

Consider two systems with transfer functions of the form

(s)=

s +1

(s)=

s +1

connected in series. The overall transfer function is given as their product

Y (s)

U(s)

s + 1)(T

s +1)

The corresponding step response function can be calculated as

y(t)=Z



1 −

− T

−

− T

−



y(t)=Z



1 −

− T



−



Consider now a second order system with the transfer function given by

G(s)=

Y (s)

U(s)

+2ζT

s +1

As it was shown in the Example 3.12, such transfer function can result

from the mathematical model of a U-tube.

The characteristic form of the step response depends on the roots of the

characteristic equation

+2ζT

s +1=0

122 4 Dynamical Behaviour of Processes

If T

represents the time constant then the dumping factor ζ plays a crucial

role in the properties of the step response. In the following analysis the

case ζ<0 will be automatically excluded as that corresponding to an

unstable system. We will focus on the following cases of roots:

Case a: ζ>1 - two diﬀerent real roots,

Case b: ζ = 1 - double real root,

Case c: 0 <ζ<1 - two complex conjugate roots.

Case a: If ζ>1 then the characteristic equation can be factorised as

follows

+2ζT

s +1=(T

s + 1)(T

s +1)

where

= T

2ζT

= T

+ T

√

ζ =

+ T

√

Another possibility how to factorise the characteristic equation is

+2ζT

s +1=



ζ −



− 1

s +1



ζ +



− 1

s +1



Now the constants T

are of the form

ζ −



− 1

ζ +



− 1

Case b: If ζ = 1 then T

= T

, T

= T

Case c: If 0 <ζ<1 then the transfer function can be rewritten as

G(s)=



2ζ

s +



and the solution of the characteristic equation is given by

1,2

−

2ζ

− 4

1,2

−ζ ±



− 1

The corresponding transfer functions are found from the inverse Laplace

transform and are of the form

Case a:

y(t)=Z



1 −

−t/T

− T

−t/T

− T



4.1 Time Responses of Linear Systems to Unit Impulse and Unit Step 123

Case b:

y(t)=Z



1 −



1 −



−t/T



Case c:

y(t)=Z

1 −



1 −ζ

−

sin





1 −ζ

t + arctan



1 −ζ

.

For the sake of completeness, if ζ = 0 the step response contains only a

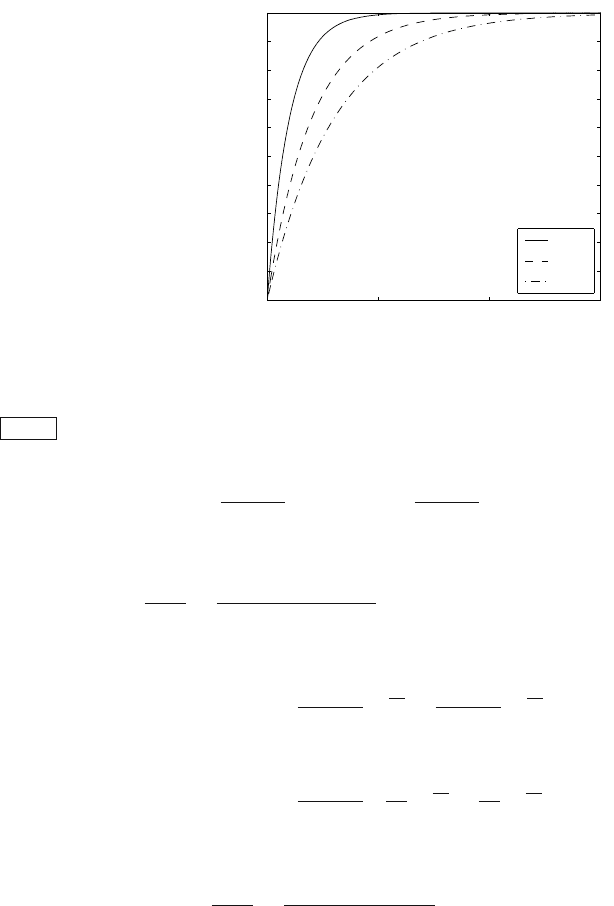
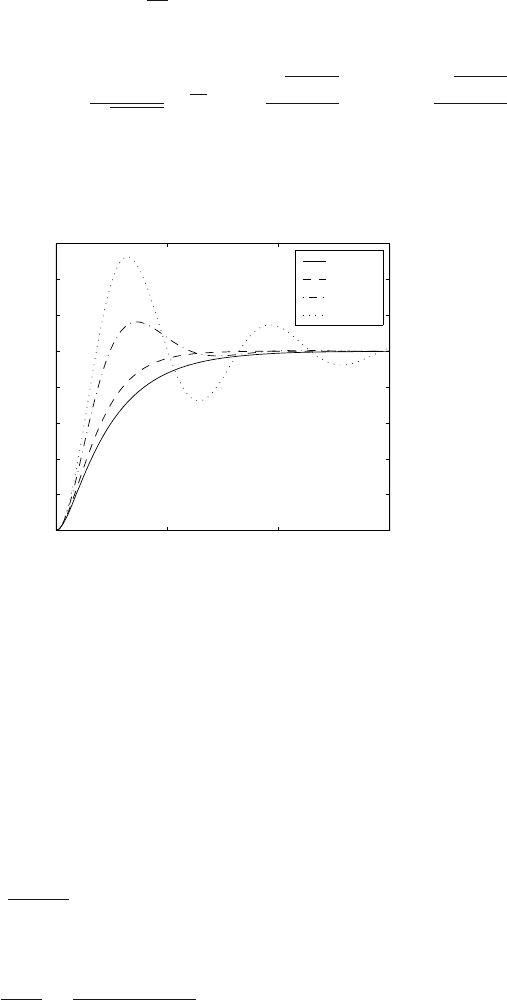
sinus function. Step responses for various values of ζ are shown in Fig. 4.4.

0 5 10 15

0.2

0.4

0.6

0.8

1.2

1.4

1.6

y / Z

ζ = 1.3

ζ = 1.0

ζ = 0.5

ζ = 0.2

Fig. 4.4. Step responses of the second order system for the various values of ζ

Consider now the system consisting of two ﬁrst order systems connected in

a series. The worst case concerning system inertia occurs if T

= T

. In this

case the tangent in the inﬂex point has the largest value. If T

 T

then

the overall characteristic of the system approaches a ﬁrst order system

with a time constant T

A generalisation of this phenomenon shows that if the system consists of

n-in-series connected systems, then the system inertia is the largest if all

time constants are equal.

If i-th subsystem is of the form

(s)=

s +1

then for the overall transfer function yields

G(s)=

Y (s)

U(s)

i=1

s +1)

124 4 Dynamical Behaviour of Processes

If T

= T

= ··· = T

then the system residence time will be the

largest. Consider unit step function on input and Z

= Z

···Z

.The

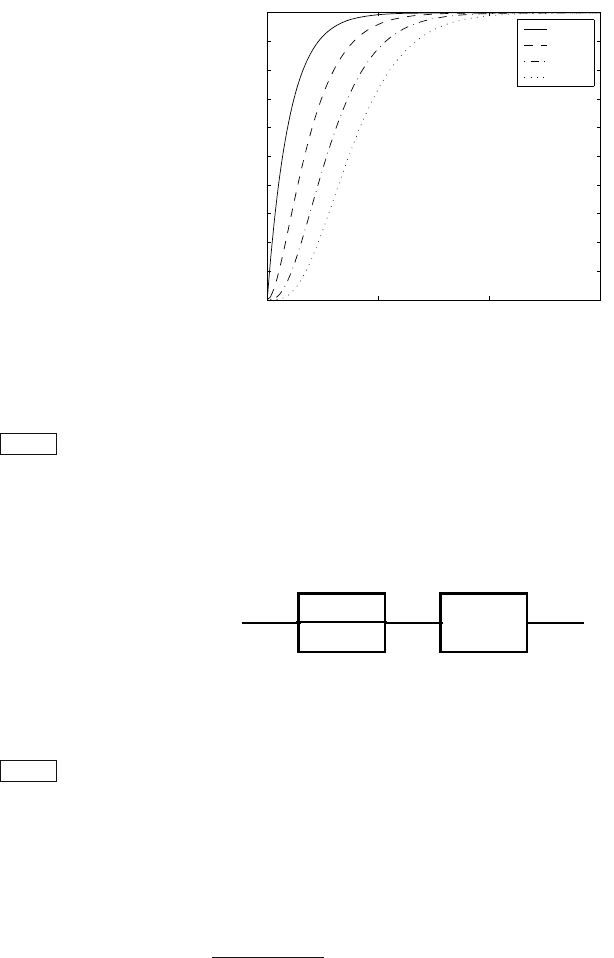
step responses for various n are given in Fig. 4.5.

0 5 10 15

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

t / T

y / Z

n = 1

n = 2

n = 3

n = 4

Fig. 4.5. Step responses of the system with n equal time constants

Example 4.4: Step response of the n-th order system connected in a serieswww

with time delay

Fig. 4.6 shows the block scheme of a system composed of n-th order system

and pure time delay connected in a series. The corresponding step response

is shown in Fig. 4.7 where it is considered that n =1.

s +1)

−T

- - -

U(s) Y (s)

Fig. 4.6. Block scheme of the n-th order system connected in a series with time

delay

Example 4.5: Step response of 2nd order system with the numerator B(s)=www

+ b

As it was shown in Example 3.14, some transfer function numerators of

the CSTR can contain ﬁrst order polynomials. Investigation of such step

responses is therefore of practical importance. An especially interesting

case is when the numerator polynomial has a positive root.

Consider for example the following system

G(s)=

s +1

+2.6s +1

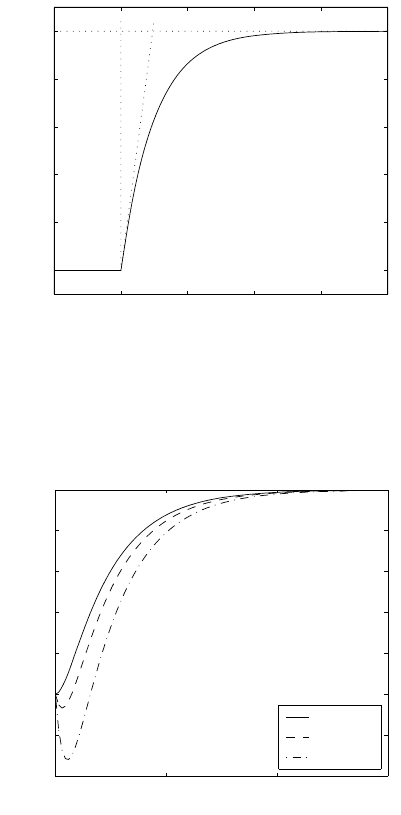
4.2 Computer Simulations 125

0 2 4 6 8 10

0.2

0.4

0.6

0.8

y / Z

Fig. 4.7. Step response of the ﬁrst order system with time delay

The corresponding step response is illustrated in Fig. 4.8.

0 5 10 15

−0.4

−0.2

0.2

0.4

0.6

0.8

y / (b

)

= 0.0

= −0.5

= −1.5

Fig. 4.8. Step response of the second order system with the numerator B(s)=b

s+1

4.2 Computer Simulations

As it was shown in the previous pages, the investigation of process behaviour

requires a solution of diﬀerential equations. Analytical solutions can only be

found for processes described by linear diﬀerential equations with constant

coeﬃcients. If the diﬀerential equations that describe dynamical behaviour of

126 4 Dynamical Behaviour of Processes

a process are nonlinear, then it is either very diﬃcult or impossible to ﬁnd the

analytical solution. In such cases it is necessary to utilise numerical methods.

These procedures transform the original diﬀerential equations into diﬀerence

equations that can be solved iteratively on a computer. The drawback of

this type of solution is a loss of generality as numerical values of the initial

conditions, coeﬃcients of the model, and its input functions must be speciﬁed.

However, in the majority of cases there does not exist any other approach as

a numerical solution of diﬀerential equations. The use of numerical methods

for the determination of process responses is called simulation. There is a

large number of simulation methods. We will explain Euler and Runge-Kutta

methods. The Euler method will be used for the explanation of principles of

numerical methods. The Runge-Kutta method is the most versatile approach

that is extensively used.

4.2.1 The Euler Method

Consider a process model in the form

dx(t)

= f(t, x(t)),x(t

)=x

(4.22)

At ﬁrst we transform this equation into its diﬀerence equation counterpart.

We start from the deﬁnition of a derivative of a function

= lim

Δt→0

x(t +Δt) −x(t)

Δt

(4.23)

if Δt is suﬃciently small, the derivative can be approximated as

x(t +Δt) −x(t)

Δt

(4.24)

Now, suppose that the right hand side of (4.22) is constant over some interval

(t, t +Δt) and substitute the left hand side derivative from (4.24). Then we

can write

x(t +Δt) −x(t)

Δt

= f(t, x(t)) (4.25)

x(t +Δt)=x(t)+Δtf (t, x(t)) (4.26)

The assumptions that led to Eq. (4.26) are only justiﬁed if Δt is suﬃciently

small. At time t = t

we can write

x(t

+Δt)=x(t

)+Δtf (t

,x(t

)) (4.27)

and at time t

= t

+Δt

4.2 Computer Simulations 127

x(t

+Δt)=x(t

)+Δtf (t

,x(t

)) (4.28)

In general, for t = t

, t

k+1

= t

+Δt Eq. (4.26) yields

x(t

k+1

)=x(t

)+Δtf (t

,x(t

)) (4.29)

Consider now the following diﬀerential equation

dx(t)

= f(t, x(t),u(t)),x(t

)=x

(4.30)

We assume again that the right hand side is constant over the interval

k+1

) and is equal to f(t

,x(t

),u(t

)). Applying the approximation (4.24)

yields

x(t

k+1

)=x(t

)+Δtf (t

,x(t

),u(t

)) (4.31)

In this equation we can notice that the continuous-time variables x(t),u(t)

have been replaced by discrete variables x(t

),u(t

). Let us denote

x(t

) ≡ x

(4.32)

u(t

) ≡ u

(4.33)

and we obtain a recursive relation called diﬀerence equation

k+1

= x

+Δtf (t

) (4.34)

that can be solved recursively for k =0, 1, 2,... for the given initial value x

Equation (4.34) constitutes the Euler method of solving the diﬀerential

equation (4.30) and it is easily programmable on a computer. The diﬀerence

h = t

k+1

− t

is usually called integration step.

As the basic Euler method is only very crude and inaccurate, the following

modiﬁcation of modiﬁed Euler method was introduced

k+1

= x

+ f

k+1

) (4.35)

where

= t

+ kh, k =0, 1, 2,...

= f(t

,x(t

),u(t

))

k+1

= f[t

k+1

,x(t

)+hf(t

,x(t

),u(t

)),u(t

k+1

)]

4.2.2 The Runge-Kutta method

This method is based on the Taylor expansion of a function. The Taylor

expansion helps to express the solution x(t +Δt) of a diﬀerential equation in

relation to x(t) and its time derivatives as follows