Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

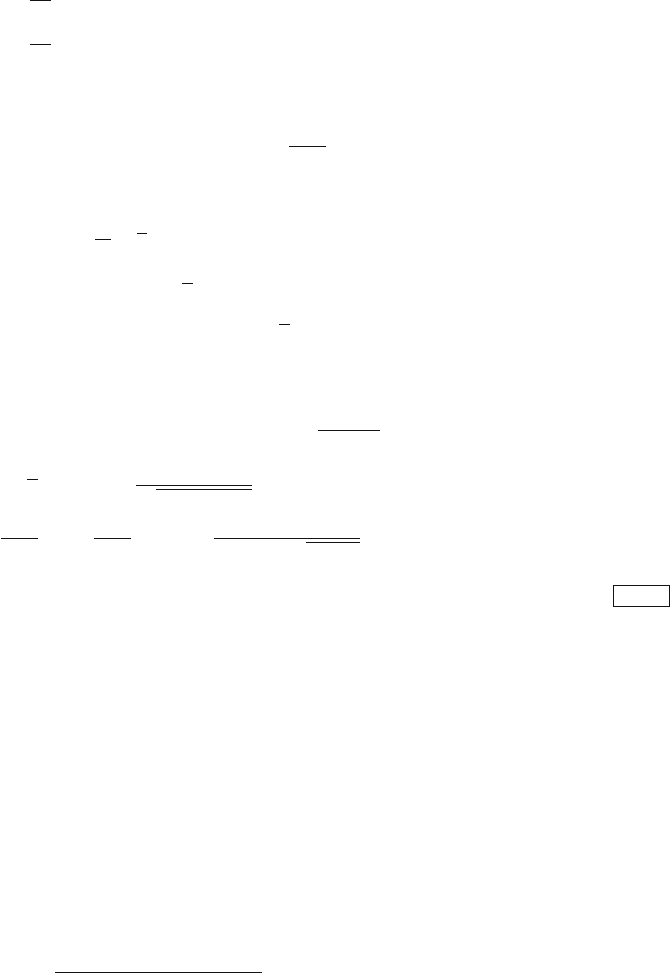
6.2 Identiﬁcation from Step Responses 229

˙y(t)=Z

−ζω

[ζ sin(ω

Pt+ ϕ) − P cos(ω

Pt+ ϕ)] (6.32)

= Z

−ζω

sin(ω

Pt) (6.33)

where the formula for sin(a − ϕ) was used. The following holds at the local

extrema

˙y(t

)=0⇐⇒ sin(ω

)=0⇒ t

nπ

(6.34)

Substituting for t

into the process output equation (6.31) yields

y(t

)=Z



1 −

−

nπζ

sin(nπ + ϕ)



(6.35)

= Z



1 −(−1)



−

πζ





(6.36)

= Z(1 −(−1)

) ,M=e

−

πζ

(6.37)

The identiﬁcation procedure is then as follows:

1. Z = y(∞),

2. y

= Z(1 + M),y

= Z(1 − M

) ⇒ M =

− y

3. M =e

−

πζ

⇒ ζ =



ln M



+ln



4. t

2π

⇒ ω

− t

)



1 −ζ

,T=1/ω

Example 6.2: Underdamped system

www

Consider a measured step response shown in the left part of Fig. 6.4 that

has been measured from the steady-state characterised by the input vari-

able at the value u

=0.2 changed to the value u

∞

= −0.3. Such a step

response can be obtained for example from a U-tube manometer by a step

change of the measured pressure.

The measured step response is ﬁrst shifted to the origin by a value of

= −2.3608 and then normalised – divided by the step change of the

input Δu =0.5. The obtained normalised step response y is shown by a

solid line on the right side of Fig. 6.4.

The values of the ﬁrst maximum and minimum are found as [15.00; 0.38]

and [30.50; 0.32], respectively. The above described identiﬁcation proce-

dure yielded the following values of the estimated parameters: Z =0.33,

ζ =0.51, and T =4.22. The approximated transfer function is then of the

form

G(s)=

0.33

17.8084s

+4.3044s +1

The step response y

of the approximated transfer function is shown by

a dashed line on the right side of Fig. 6.4.

230 6 Process Identiﬁcation

0 10 20 30 40 50

−2.55

−2.5

−2.45

−2.4

−2.35

−2.3

0 10 20 30 40 50

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

Fig. 6.4. Measured step response of an underdamped system (left). Normalised and

approximated step response (right)

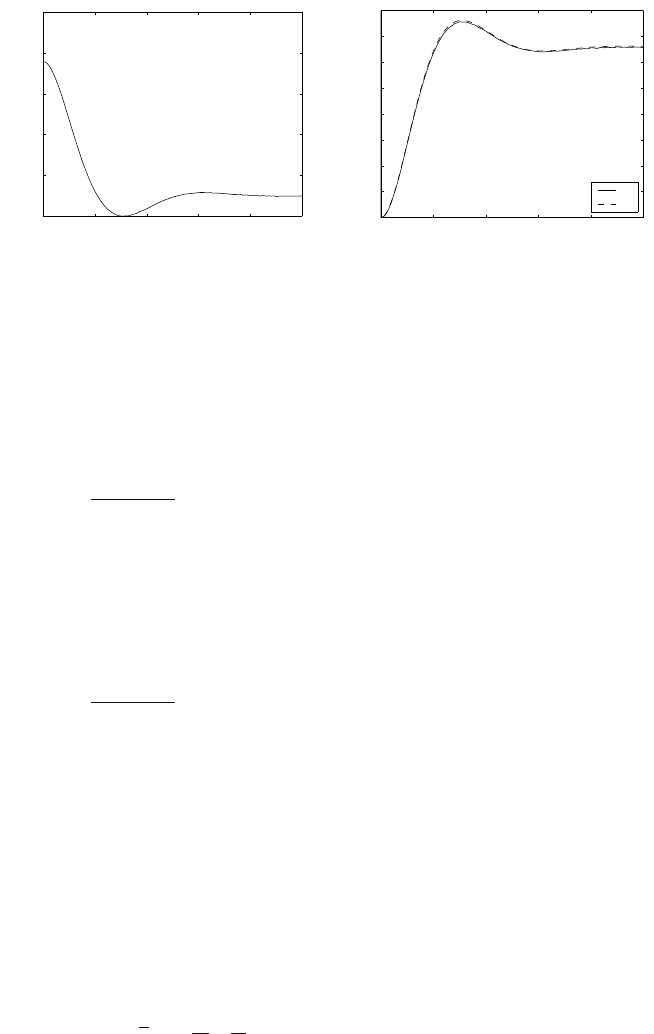
6.2.3 System of a Higher Order

Strejc Method

Consider an approximation of a process by the nth order system

G(s)=

(Ts+1)

−T

(6.38)

where Z is the process gain, T time constant, T

time delay, and n the system

order that all are to be estimated. Two process characteristics are determined

from the step response: times T

, T

(see page 257) from the tangent at the

inﬂexion point.

Consider now properties of the normalised step response if T

= 0 (Fig. 6.5)

G(s)=

(Ts+1)

(6.39)

The following facts will be used for the derivation:

1. The tangent of the step response in the inﬂexion point [t

] is given by

the equation of a line p : y = a + bt,

2. The line p passes through points [T

, 0], [T

+ T

, 1], [t

]. The following

holds: b =1/T

and a = −T

3. The slope of the line p is given as b =˙y(t

4. ¨y(t

) = 0 (inﬂexion point).

The step response can by obtained by the means of the inverse Laplace

transform and is given as

y(t)=1− e

−

n−1



k=0





(6.40)

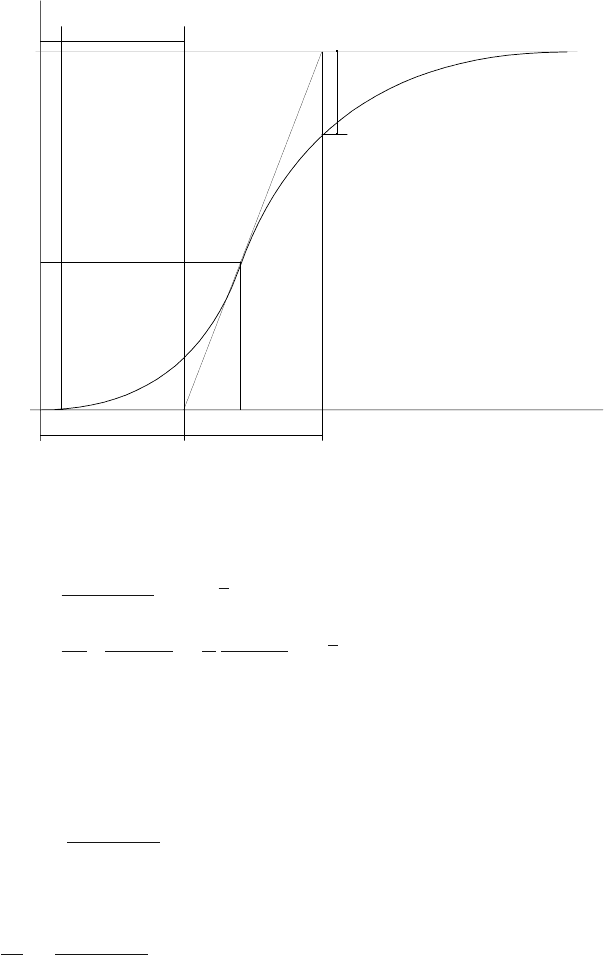
6.2 Identiﬁcation from Step Responses 231

- -

--

e(T

)

Fig. 6.5. Step response of a higher order system

We calculate the ﬁrst and the second derivative of the output y with respect

to time

˙y(t)=

(n −1)!

n−1

−

(6.41)

¨y(t)=



n−2

(n −2)!

−

n−1

(n −1)!



−

(6.42)

In the inﬂexion point holds ¨y(t

) = 0, hence

= T (n −1) (6.43)

Evaluating ˙y at time t

gives

˙y(t

(n −1)

n−1

T (n −1)!

−(n−1)

(6.44)

It can be seen from the ﬁgure that ˙y(t

)=1/T

,thus

(n −1)

n−1

(n −1)!

−(n−1)

= g(n) (6.45)

We can see that this function depends only on n.

Further, it can be shown that the relation between T

and T

is again only

a function of n

232 6 Process Identiﬁcation

−(n−1)

(n −1)

(n −1)!

n−1



k=0

(n −1)

− 1=f(n) (6.46)

The following table can then be constructed:

123456

f(n) 0.000 0.104 0.218 0.319 0.410 0.493

g(n)

1.000 0.368 0.271 0.224 0.195 0.161

The identiﬁcation procedure is then as follows:

1. The values of Z = y(∞), T

are read from the step response,

2. The quotient f

= T

is calculated,

3. The degree n

is chosen from the table in such a way that the following

holds

f(n

) ≤ f

<f(n

+1),

4. Time delay T

can be determined as the diﬀerence between the real and

theoretical time T

=[f

− f(n

)]T

because T

= T

f(n),

5. The process time constant T can be read from the row of g(n) for the

corresponding n

. T is obtained from the deﬁnition of g

T = T

g(n

Broida method

The assumption that all time constants of the process are the same may not

always hold. Broida considered the transfer function of the form

G(s)=

k=1

(

s +1)

−T

(6.47)

In the same way as in the Strejc method, the table for f(n),g(n)canbe

derived.

123456

f(n) 0.000 0.096 0.192 0.268 0.331 0.385

g(n)

1.000 0.500 0.440 0.420 0.410 0.400

The identiﬁcation procedure is the same as with the Strejc method.

Example 6.3: Higher order system approximation

www

Consider again identiﬁcation of the step response of the chemical reactor

from Example 6.1. Inﬂexion point has been determined, tangent drawn

6.3 Least Squares Methods 233

that crosses it, and times T

=0.2451 a T

=1.9979 were read (Fig. 6.6

left).

Both Strejc and Broida methods were applied. Resulting transfer functions

are given as

Strejc

(s)=

0.027

0.54s

+1.47s +1

−0.037s

Broida

(s)=

0.027

0.5s

+1.5s +1

−0.053s

The step responses together with the original one are shown in Fig. 6.6

(right). We can notice that both methods approximate the process dynam-

ics better than the ﬁrst order transfer function. However, neither Strejc

nor Broida methods can cover small overshoot as both are suitable only

for aperiodic and monotone step responses.

0 2 4 6 8 10

0.005

0.01

0.015

0.02

0.025

0.03

0 2 4 6 8 10

0.005

0.01

0.015

0.02

0.025

0.03

orig

strejc

broida

Fig. 6.6. Normalised step response of the chemical reactor with lines drawn to

estimate T

(left), approximated step response (right)

6.3 Least Squares Methods

The most often used methods nowadays are based on minimisation of squares

of errors between measured and estimated process output – the least squares

method (RL). Main advantages include the possibility of recursivity of calcu-

lations, possibility to track time variant parameters, and various modiﬁcations

to make the algorithm robust. Originally the method was derived for estima-

tion of parameters of discrete-time systems. We will also show its modiﬁcation

for continuous-time systems.

Consider the ARX model (see page 224).

y(k)=−a

y(k−1)−···−a

y(k−n

)+b

u(k−1)+···+b

u(k−n

)+ξ(k)

(6.48)

234 6 Process Identiﬁcation

We will introduce the notation

=(a

,...,a

,...,b

)

(k)=(−y(k − 1),...,−y(k −n

),u(k − 1),...,u(k − n

))

Hence

y(k)=θ

z(k)+ξ(k) (6.49)

The identiﬁcation aim is to determine the parameter vector θ based on infor-

mation of measured process output y(k) and the data vector z(k).

Assume that the equation (6.49) holds at times 1,...,k

y(1) = −

i=1

y(1 −i)+

i=1

u(1 −i)+ξ(1) = z

(1)θ + ξ(1)

y(2) = −

i=1

y(2 −i)+

i=1

u(2 −i)+ξ(2) = z

(2)θ + ξ(2)

y(k)=−

i=1

y(k − i)+

i=1

u(k − i)+ξ(k)=z

(k)θ + ξ(k)

(6.50)

where k>n

+ n

and denote

Y =

⎛

⎜

⎝

y(1)

y(2)

y(k)

⎞

⎟

⎠

, ξ =

⎛

⎜

⎝

ξ(1)

ξ(2)

ξ(k)

⎞

⎟

⎠

(6.51)

Z =

⎛

⎜

⎝

(1)

(2)

(k)

⎞

⎟

⎠

(6.52)

We will look for such an estimate

θ that minimises sum of squares of errors

between measured and modelled outputs, i. e.

I(θ)=



i=1

(y(i) −z

(i)θ)

(6.53)

This equation can be rewritten in vector notation

I(θ)=(Y − Zθ)

(Y −Zθ) (6.54)

Minimum is found if gradient of this function with respect to θ is equal to

zero

θ = Z

Y (6.55)

6.3 Least Squares Methods 235

If the matrix Z

Z is invertible, then

θ =(Z

−1

Y (6.56)

The matrix P =(Z

−1

is called the covariance matrix if the stochastic

part has unit variance.

In general, the estimate of

θ is unbiased (its expectation is equal to θ)if

ξ(k) is white noise.

6.3.1 Recursive Least Squares Method

In recursive least squares (RLS) estimated parameters are improved with each

new data. This means that the estimate

θ(k) can be obtained by some simple

manipulations from the estimate

θ(k − 1) based on the data available up to

time k − 1.

Characteristic features of recursive methods are as follows:

• Their requirements for computer memory are very modest as not all mea-

sured data up to current time are needed.

• They form important part of adaptive systems where actual controllers

are based on current process estimates.

• They are easily modiﬁable for real-time data treatment and for time vari-

ant parameters.

To understand better derivation of a recursive identiﬁcation method, let

us consider the following example.

Example 6.4: Recursive mean value calculation

Consider a model of the form

y(k)=a + ξ(k)

where ξ(k) is a disturbance with standard deviation of one. It is easy to

show that the best estimate of a based on information up to time k in the

sense of least squares is given as the mean of all measurements

ˆa(k)=



i=1

y(i)

This equation can be rewritten as

ˆa(k)=

k−1



i=1

y(i)+y(k)

[(k − 1)ˆa(k − 1) + y(k)]

=ˆa(k − 1) +

[y(k) − ˆa(k − 1)]

The result says that the estimate of the parameter a in time k is equal

to the estimate at time k − 1 plus some correction term. The correction

term depends linearly on the error between ˆa(k −1) and its prediction at

236 6 Process Identiﬁcation

time k,i.e.y(k). The proportionality factor is 1/k which means that the

magnitude of changes will be decreasing with increasing time as the value

of ˆa(k − 1) will approach the true value of a.

Similarly, it can be shown that the covariance matrix is given as P (k)=

1/k. This relation can recursively be rewritten as

P (k)=

P (k − 1)

1+P (k − 1)

The following matrix inversion lemma will be used to derive recursive least

squares method.

Theorem 6.1. Assume that M = A + BC

−1

D. If the matrices A, C are

nonsingular, then

−1

= A

−1

− A

−1

B(DA

−1

B + C)

−1

(6.57)

Proof. Consider inversion of a matrix X

−1



−DC



−1





= P (6.58)

Because XP = I, multiplication of all submatrices gives

+ BP

= I, AP

+ BP

= 0 (6.59)

−DP

+ CP

= 0, −DP

+ CP

= I (6.60)

We assume that A, C are nonsingular. Hence

= C

−1

, P

= −A

−1

=[A + BC

−1

, P

=[C + DA

−1

(6.61)

As it also holds that PX = I we can write

A −P

D = I ⇒ P

= A

−1

+ P

−1

(6.62)

Comparison of the last three equations yields the desired result. 

If we consider C =1, B = b, D = b

then the matrix inversion lemma yields

−1

=(A + bb

)

−1

= A

−1

− A

−1

b(b

−1

b +1)

−1

(6.63)

where the term that has to be inverted is only a scalar.

To derive the RLS method assume that the parameter estimate at time

k denoted by

θ(k) given by (6.56) and the covariance matrix P (k)=

(k)Z(k))

−1

are known. The aim is to derive recursive relations for

θ(k+1)

and P (k + 1). When the measurement at time k + 1 is known then

6.3 Least Squares Methods 237

Y (k +1)=



Y (k)

y(k +1)



Z(k +1)=



Z(k)

(k +1)



, Z

(k +1)=



(k) z(k +1)



The covariance matrix P (k + 1) is given as

P (k +1)=(Z

(k +1)Z(k + 1))

−1

(6.64)





(k) z(k +1)





Z(k)

(k +1)



−1

(6.65)



(k)Z(k)+z(k +1)z

(k +1)



−1

(6.66)



P (k)

−1

+ z(k +1)z

(k +1)



−1

(6.67)

Using the matrix inversion lemma yields

P (k+1) = P (k)−P (k)z(k+1)[z

(k+1)P (k)z(k+1)+1]

−1

(k+1)P (k)

(6.68)

Denote γ(k +1)=[z

(k +1)P (k)z(k +1)+1]

−1

. This can be manipulated

γ(k +1)=1− γ(k +1)z

(k +1)P (k)z(k + 1) (6.69)

This relation will later be used.

Therefore, the covariance matrix P update is given as

P (k +1)=P (k) − γ(k +1)P (k)z(k +1)z

(k +1)P (k) (6.70)

Derivation of a new parameter estimate

θ(k + 1) is similar and makes use

of (6.69), (6.70):

k+1

= P (k +1)Z

(k +1)Y (k +1)

= P (k +1)



(k) z(k +1)





Y (k)

y(k +1)



= P (k + 1)[Z

(k)Y (k)+z(k +1)y(k + 1)]

=[P (k) −γ(k +1)P (k)z(k +1)z

(k +1)P (k)] ×

(k)Y (k)+z(k +1)y(k + 1)]

θ(k) −γ(k +1)P (k)z(k +1)z

(k +1)

θ(k)

+P (k)z(k +1)y(k +1)

−γ(k +1)P (k)z(k +1)z

(k +1)P (k)z(k +1)y(k +1)

θ(k) −γ(k +1)P (k)z(k +1)z

(k +1)

θ(k)

+P (k)z(k + 1)[1 − γ(k +1)z

(k +1)P (k)z(k + 1)]y(k +1)

θ(k) −γ(k +1)P (k)z(k +1)z

(k +1)

θ(k)

+γ(k +1)P (k)z(k +1)y(k +1)

θ(k)+γ(k +1)P (k)z(k + 1)[y(k +1)− z

(k +1)

θ(k)] (6.71)

238 6 Process Identiﬁcation

To conclude, equations for recursive least squares are given as

(k +1)=y(k +1)− z

(k +1)

θ(k)

γ(k +1)=[1+z

(k +1)P (k)z(k + 1)]

−1

L(k +1)=γ(k +1)P (k)z(k +1)

P (k +1)=P (k) − γ(k +1)P (k)z(k +1)z

(k +1)P (k)

θ(k +1)=

θ(k)+L(k +1)(k +1)

(6.72)

Every recursive algorithm needs some initial conditions. In our case these

are

θ(0) and P (0). The value of P (0) can be thought as uncertainty of the

estimate

θ(0). Both initial conditions have some inﬂuence on convergence

properties of RLS. As it will be shown below, the cost function minimised by

RLS is not given by (6.53), but as

k+1

(θ)=[θ −

θ(0)]

−1

(0)[θ −

θ(0)] +

k+1



i=1

[y(i) −z

(i)θ]

(6.73)

We can notice that the original cost function includes a term characterising

eﬀects of initial conditions. To minimise these eﬀects we usually choose

θ(0) =

0 and P (0) = cI where c is some large constant, for example 10

− 10

For completeness we will give the proof of above mentioned statements

Theorem 6.2. Minimisation of the cost function (6.73) leads to (6.72).

Proof. The cost function (6.73) can be rewritten to the vector notation

k+1

(θ)=[θ −

θ(0)]

−1

(0)[θ −

θ(0)]

+[Y (k +1)−Z(k +1)θ]

[Y (k +1)− Z(k +1)θ] (6.74)

Setting its partial derivative with respect to θ equal to zero gives

(k +1)Z(k +1)+P

−1

(0)]θ = P

−1

(0)

θ(0) + Z

(k +1)Y (k + 1) (6.75)

Data up to time k + 1 gives

θ(k + 1), thus

θ(k+1) = [Z

(k+1)Z(k+1)+P

−1

(0)]

−1

(0)

θ(0)+Z

(k+1)Y (k+1)]

(6.76)

Recursion of (6.67) gives the relation

−1

(k +1)=P

−1

(0) + Z

(k +1)Z(k + 1) (6.77)

and for the estimate of the parameters

θ(k + 1) holds

θ(k +1)=P (k + 1)[P

−1

(0)

θ(0) + Z

(k +1)Y (k + 1)] (6.78)

= P (k + 1)[P

−1

(0)

θ(0) + Z

(k)Y (k)+z(k +1)y(k + 1)] (6.79)

Equation (6.76) shifted to time k is given as