Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

6.3 Least Squares Methods 239

θ(k)=P (k)[P

−1

(0)

θ(0) + Z

(k)Y (k)] (6.80)

and equation (6.79) can be rewritten as

θ(k +1)=P (k + 1)[P

−1

(k)

θ(k)+z(k +1)y(k + 1)] (6.81)

Substituting for P

−1

(k) from (6.67) yields

θ(k +1)=

θ(k) −P (k + 1)[z(k +1)z

(k +1)

θ(k)+z(k +1)y(k + 1)](6.82)

θ(k)+P (k +1)z(k +1)(k + 1) (6.83)

We can see that this relation would be equivalent to the last of equations (6.72)

P (k +1)z(k +1)=γ(k +1)P (k)z(k + 1) (6.84)

Substituting for P (k + 1) from (6.70) gives

[P (k) −γ(k +1)P (k)z(k +1)z

(k +1)P (k)]z(k +1)

= γ(k +1)P (k)z(k +1)

γ(k +1)P (k)z(k + 1)[1 + z

(k +1)P (k)z(k + 1)] = P (k)z(k +1)

The term in square brackets is nothing else than γ

−1

(k +1) which ﬁnishes the

proof. 

Convergence of Parameters

Let us assume that the identiﬁed system model structure is the same as

the true system. The question then arises whether the data set is informa-

tive enough and in consequence whether the identiﬁcation procedure yields a

unique value of the identiﬁed vector

θ.

Whether a model described by a diﬀerence equation is identiﬁable correctly

by the RLS method depends on nonsingularity of its covariance matrix and

on the input signal u(k). The covariance matrix can be given as

−1

(k)=



i=1

z(i)z

(i) (6.85)

The necessary condition for invertibility of this matrix is that k ≥ n where n

is dimension of the data vector z(k). The suﬃcient condition is connected to

the idea of persistence of excitation (PE) of the process input. To understand

this concept let us consider the FIR class of models (see page 224) of the form

y(k)=



i=1

u(k − i)+ξ(k) (6.86)

240 6 Process Identiﬁcation

The parameter and data vectors are of the form

=[b

,...,b

] (6.87)

z(k)

=[u(k − 1),...,u(k − n)] (6.88)

Comparing with (6.85) gives the condition for persistence of excitation of the

input u(k): the process input u(k)ispersistently exciting of order n if

I >

k+l



i=k

[u(i −1),...,u(i − n)]

[u(i −1),...,u(i − n)] >m

I (6.89)

where m

> 0andl is a positive integer (necessary condition implies

l ≥ n).

We can then state

Theorem 6.3. RLS for the FIR system (6.86) converges to θ if

1. the process input u(k) is persistently exciting of order at least n.

If ARX model is considered of the form

y(k)=−



i=1

y(k − i)+



i=1

u(k − i)+ξ(k) (6.90)

then the convergence conditions are the following:

Theorem 6.4. RLS for the ARX system (6.90) converges to θ if

1. polynomials A, B are coprime,

2. the system is stable,

3. the process input u(k) is persistently exciting of order at least 2n.

In general, parameter estimation using RLS as described above can be

used only for stable systems. This was stated in the previous theorem. For

unstable systems it is necessary to stabilise the controlled process at ﬁrst

by some controller. However, in that case parameter convergence cannot be

guaranteed as u(k) is generated as a linear combination of the data vector

z(k)

u(k)=−Kz(k) (6.91)

If the control law is given by the previous relation, convergence of parameters

cannot be assured. However, the problem can be solved by addition of an

external signal to the closed-loop system that will be persistently exciting.

Theorem 6.5. RLS for the system (6.90) converges to θ if

1. polynomials A, B are coprime,

2. the process input u(k) is generated from the feedback control law of the

form

u(k)=−Kz(k)+v(k) (6.92)

3. external signal v(k) is persistently exciting of order at least 4n.

6.3 Least Squares Methods 241

6.3.2 Modiﬁcations of Recursive Least Squares

Equation (6.67) for the covariance matrix update gives

−1

(k +1)=P

−1

(k)+z(k +1)z

(k + 1) (6.93)

This relation can be generalised to the form

−1

(k +1)=λ

(k)P

−1

(k)+λ

(k)z(k +1)z

(k + 1) (6.94)

where 0 <λ

(k) ≤ 1, 0 ≤ λ

(k) < 2. We note that λ

,λ

have opposite eﬀects.

increases the covariance matrix and λ

decreases it. This modiﬁcation also

leads to change in γ(k + 1), as well as in L(k + 1).

Recursive formula for the covariance matrix is then given as

γ(k +1)=

(k)/λ

(k)+z

(k +1)P (k)z(k +1)

(6.95)

P (k +1)=

(k)



P (k) −γ(k +1)P (k)z(k +1)z

(k +1)P (k)



(6.96)

Various strategies for choices of λ

give diﬀerent modiﬁcations of the identiﬁ-

cation algorithm.

Decreasing gain The basic setting is λ

= λ

= 1. The identiﬁcation gain

decreases and the covariance matrix increases. This choice is suitable for

identiﬁcation of constant parameters.

Constant exponential forgetting if λ

< 1, λ

= 1. Typical values of λ

are

between 0.95 and 0.99. The cost function can then be written as

I(k)=



i=1

k−i



(6.97)

We can see that the eﬀect of λ

is in forgetting the older data as the

most important are the most recent data. This identiﬁcation algorithm is

suitable in case when the identiﬁed parameters change slowly.

Increasing exponential forgetting In this case is λ

= 1 and exponential for-

getting λ

is given as

(k)=λ

(k − 1) + 1 −λ

(6.98)

with typical initial conditions

(0) = λ

∈0.95, 0.99 (6.99)

This form of exponential forgetting asymptotically converges to one and

only initial data are forgotten.

This modiﬁcation is used for systems with constant parameters. Initial

data are considered uncertain and are forgotten.

242 6 Process Identiﬁcation

Varying exponential forgetting In this case is λ

= 1 and exponential forget-

ting λ

is given as

(k)=1− kγ(k)

(k) (6.100)

where the constant k is a small positive number (for example 0.001).

In this case the algorithm works as follows: if the identiﬁed process

changes, the prediction error 

will increase and results in a decrease

of λ

. Older data will be forgotten more quickly. If 

decreases, the pro-

cess is well identiﬁed, λ

approaches the its upper limit and the rate of

forgetting will be slower.

Constant trace In this case are λ

chosen in such a way that the trace of the

covariance matrix will be constant

trP (k +1)=trP (k)=ng (6.101)

where n is the number of identiﬁed parameters and g =0.1 − 4 is initial

gain.

This modiﬁcation is suitable for estimation of time-varying parameters.

Constant gain In this case is λ

=1,λ

= 0 and the covariance matrix is

given as

P (k +1)=P (k)=P (0) (6.102)

This algorithm can be used for identiﬁcation of a small number of param-

eters (≤ 3) if the signal-to-noise ratio is small. Convergence of parameters

is usually smaller but the algorithm can be easily implemented.

Also used are combinations of the above mentioned methods, e. g. constant

trace with exponential forgetting. These implementations are suitable for es-

timation of time-varying parameters if initial estimates are poor.

There is one drawback of recursive methods with exponential forgetting.

If there are no new data (z(k +1)=z(k)) it can happen that the covariance

matrix increases and is no longer positive deﬁnite. The algorithm will break

down (so called bursting eﬀect). In general it is recommended to check the

trace of the covariance matrix.

A method has been developed to improve stability that forgets only in that

direction from which some new information comes. The formulas describing

this method are as follows:

r(k)=z(k +1)

P (k)z(k + 1) (6.103)

L(k +1)=

P (k)z(k +1)

1+r(k)

(6.104)

β(k)=

(k) −

1−λ

(k)

r(k)

if r(k) > 0

1ifr(k)=0

(6.105)

P (k +1)=P (k) −

P (k)z(k +1)z(k +1)

P (k)

β(k)

−1

+ r(k)

(6.106)

6.3 Least Squares Methods 243

When the factorisation of the covariance matrix P = LDL

is employed

(where L is a lower triangular and D diagonal matrix), this method is known

under the name LDDIF and is used throughout the book in adaptive control

of processes.

Another approach to estimate better time-varying parameters consists in

a direct modiﬁcation of the covariance matrix P . It is clear that the main di-

agonal contains information about dispersion of the parameters. If the param-

eters are time varying, it is possible to increase dispersions and thus speed-up

adaptation to new parameter values

P (k +1)=P (k +1)+δI (6.107)

where δ<0.01.

Another possibility is to selectively turn oﬀ RLS method if the parameter

estimates are correct. Similarly to the case of the variable exponential forget-

ting, the prediction error is checked. If it is small then the parameters will be

held constant. We deﬁne a parameter α

α(k)=



1ifγ(k)

(k) >ε

> 0

0 otherwise

(6.108)

where ε is a small positive number. Then equations (6.72) are of the form

P (k +1)=P (k) − α(k +1)γ(k +1)P (k)z(k +1)z

(k +1)P (k)

θ(k +1)=

θ(k)+α(k +1)L(k +1)(k +1)

(6.109)

This will guarantee that the covariance matrix and parameter estimates will

not change if the process output and the model output agree.

Example 6.5: Second order system identiﬁcation

www

For the second order system with the transfer function of the form

G(z)=

−1

+ b

−2

1+a

−1

+ a

−2

is the data vector given as

(k)=[−y(k − 1), −y(k − 2),u(k − 1),u(k − 2)]

in each sampling time. The parameter vector corresponding to the data

vector is then given as

θ =[a

]

Consider for example a

=0.5, a

=0.1, b

=0.4, b

=0.2. The Simulink

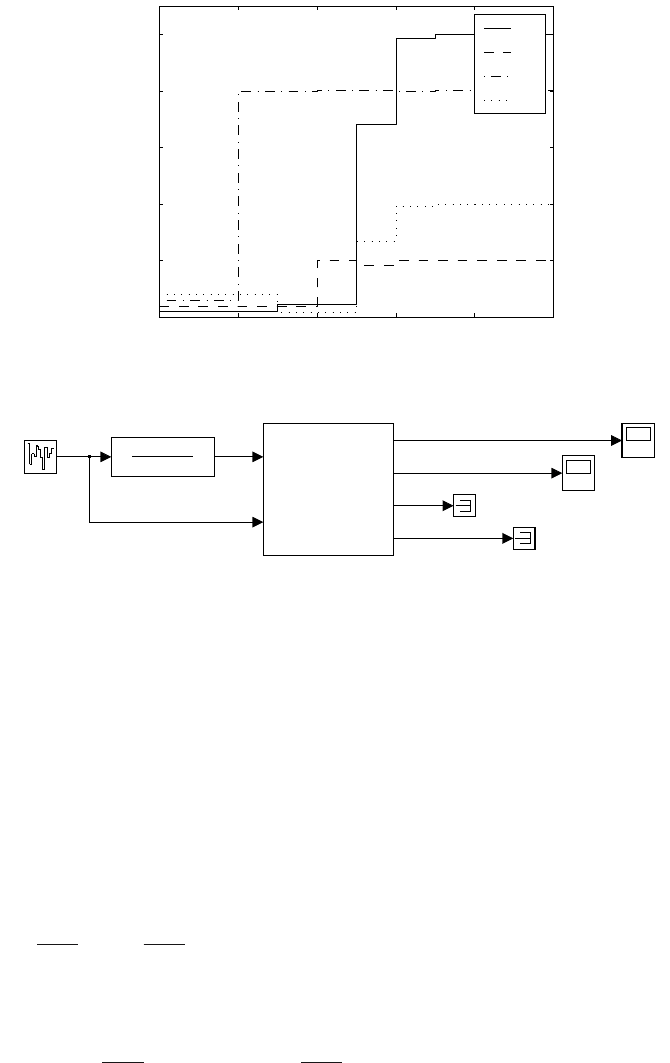
schema for identiﬁcation is shown in Fig. 6.7 and trajectories of estimated

parameters are in Fig. 6.8. We can notice that parameters converge to

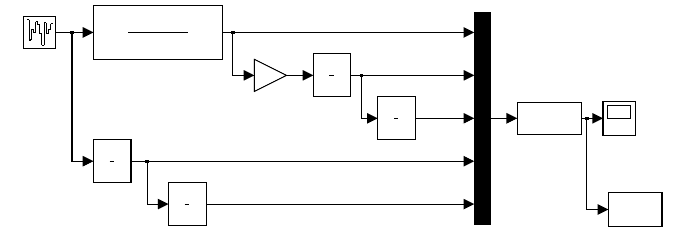
244 6 Process Identiﬁcation

nominal values. The block denoted as rls is the S-function for recursive

least squares and its code is shown in Program 6.1.

Alternatively, numerically robust implementation of the scheme in Fig. 6.7

using blocks from Simulink library IDTOOL with recursive least squares

algorithm LDDIF is shown in Fig. 6.9.

Unit Delay3

Unit Delay2

Unit Delay1

Unit Delay

data

To Workspace

rls

S−Function

.4z +.2z

−1 −2

1+0.5z +.1z

−1 −2

Process

Parameters

−1

Gain

Band−Limited

White Noise

y(k)

u(k−1)

−y(k−1)

−y(k−2)

u(k−2)

Fig. 6.7. Simulink schema for parameter estimation of the second order discrete

system

Program 6.1 (S-function for RLS (rls.m))

function [sys,x0,str,ts] = rls(t,x,u,flag,tsamp,n)

% tsamp - sampling time

% n: length of the input vector

% (n = num. of parameters + 1)

% u = [y; z]

switch flag,

case 0,

[sys,x0,str,ts]=mdlInitializeSizes(tsamp,n-1);

case 2,

sys=mdlUpdate(t,x,u,n-1);

case 3,

sys=mdlOutputs(t,x,u,n-1);

case 9,

sys=mdlTerminate(t,x,u);

otherwise

error([’Unhandled flag = ’,num2str(flag)]);

end

function [sys,x0,str,ts]=mdlInitializeSizes(tsamp,n)

sizes = simsizes;

6.3 Least Squares Methods 245

sizes.NumContStates = 0;

sizes.NumDiscStates = n*(n+1);

sizes.NumOutputs = n;

sizes.NumInputs = n+1;

sizes.DirFeedthrough = 0;

sizes.NumSampleTimes = 1;

sys = simsizes(sizes);

theta=(1:n)’*0.01;

p=eye(n,n)*1e6;

x0 = [theta;p(:)];

str = [];

ts = [tsamp 0];

function sys=mdlUpdate(t,x,u,n)

p =zeros(n,n);

theta=zeros(n,1);

theta(:)=x(1:n);

p(:)=x(n+1:n+n*n);

y=u(1);

z=u(2:n+1);

% begin

e=y-z’*theta;

gamma=1/(1+z’*p*z);

l=gamma*p*z;

p=p-gamma*p*z*z’*p;

theta=theta+l*e;

% end

sys = [theta(:);p(:)];

function sys=mdlOutputs(t,x,u,n)

sys=x(1:n);

function sys=mdlTerminate(t,x,u)

sys = [];

6.3.3 Identiﬁcation of a Continuous-time Transfer Function

Consider a diﬀerential equation of a linear continuous-time system

A(p)y(t)=B(p)u(t) (6.110)

246 6 Process Identiﬁcation

0 2 4 6 8 10

0.1

0.2

0.3

0.4

0.5

Param

Fig. 6.8. Estimated parameter trajectories for the second order discrete system

Terminator1

Terminator

.4z +.2z

−1 −2

1+0.5z +.1z

−1 −2

Process

Numerator

D. identification

SISO

Discrete identification

Denominator

Band−Limited

White Noise

u(k)

y(k)

Fig. 6.9. Alternate Simulink schema for parameter estimation of the second order

discrete-time system using blocks from library IDTOOL

where p =d/dt is the derivative operator and the polynomials are given as

A(p)=a

+ a

p + ···+ a

n−1

+ p

(6.111)

B(p)=b

+ b

p + ···+ b

(6.112)

We assume that the process is strictly proper, i. e. the degree of the polynomial

B(p) is lower than the degree of the polynomial A(p).

If derivatives of inputs and outputs were available, we could directly esti-

mate coeﬃcients of the polynomials a

. However, the derivatives are usually

not measurable. Therefore, equation (6.110) will be divided by a stable poly-

nomial C(p)

A(p)

C(p)

y(t)=

B(p)

C(p)

u(t) (6.113)

A(p)y

(t)=B(p)u

(t) (6.114)

where

(t)=

C(p)

y(t),u

(t)=

C(p)

u(t) (6.115)

6.3 Least Squares Methods 247

We can see that it is also possible to estimate the parameters from (6.114).

All necessary derivatives of ﬁltered variables are available from (6.115) under

the conditions that the degree of the polynomial C is greater or equal to the

degree of the polynomial A.

If the degrees are equal, the ﬁlter is of a minimum realisation. If the degree

of C is greater, the ﬁlter is strictly proper.

The structure of the C polynomial is usually chosen as

C(p)=(1+c

(6.116)

where c

is the time constant of the ﬁlter and its value should be smaller than

the smallest time constant of A polynomial.

If signals u

, y

and their derivatives will be measured at sampling times

= kT

then the identiﬁcation problem can be posed as follows

(n)

(k)=θ

z(k)+ξ(k) (6.117)

=(a

, ..., a

, ..., b

) (6.118)

(k)=(−˙y

(k), ..., −y

(n−1)

(k),u

(k), ˙u

(k), ..., u

(m)

(k)) (6.119)

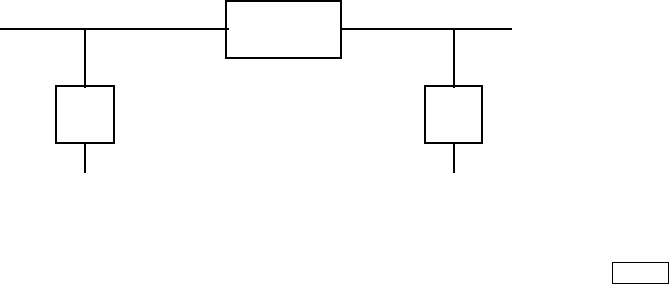
The block scheme of this procedure is shown in Fig. 6.10.

1/C

B/A

1/C

- -

Fig. 6.10. Block scheme of identiﬁcation of a continuous-time transfer function

Example 6.6: Second order system www

Consider identiﬁcation of a continuous-time second order system of the

form

¨y + a

˙y + a

y = b

u + b

˙u

We introduce a stable second order ﬁlter C(p)

C(p)=(1+c

and ﬁltered variables

C(p)y

= y, C(p)u

= u

248 6 Process Identiﬁcation

If state variables are x

= y

, x

=˙y

then the output ﬁlter equation is

in the state-space form given as



˙x





−









⎛

⎝

⎞

⎠

⎛

⎝

−

−10

0 −1

⎞

⎠





⎛

⎝

⎞

⎠

where the state-space outputs are z

=¨y

, z

= −y

, z

= −˙y

We can deﬁne states for the input ﬁlter similarly as x

= u

, x

=˙u

and

the state-space description is then given as



˙x





−























where the state-space outputs are z

= u

, z

=˙u

The diﬀerential equation of the system is now of the form

¨y

= −a

− a

˙y

+ b

˙u

= a

+ a

+ b

Hence

=(a

)

=(z

)

Consider for example a

=2,a

=3,b

=1,b

= −1. We choose a second

order ﬁlter with the time constant c

=0.25 and the sampling period for

identiﬁcation T

= 1. State ﬁlters for output A, B, C

, D

and for input

A, B, C

, D

are given as

A =



−16 −8



, B =





, C

⎛

⎝

−16 −8

−10

0 −1

⎞

⎠

, D

⎛

⎝

⎞

⎠





, D





Simulink schema is shown in Fig. 6.11 and trajectories of estimated pa-

rameters are in Fig. 6.12. We can see that convergence has been achieved

within a few sampling steps.

Alternatively, numerically robust implementation of the scheme shown in

Fig. 6.11 using blocks from Simulink library IDTOOL with recursive least

squares algorithm LDDIF is shown in Fig. 6.13.