Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

270 7 The Control Problem and Design of Simple Controllers

controlled system. When pole locations are considered for the original

(s = −1/T

) and closed-loop system, the closed-loop pole is pushed more

to the left half part of the complex plane. This also means that an unstable

system can be stabilised by the P controller with a suﬃciently high gain

that causes the closed-loop pole moved to the left of the imaginary axis.

Example 7.6: Proportional control of a higher order system

www

Consider again proportional control of a system with the transfer function

G(s)=

(s +1)

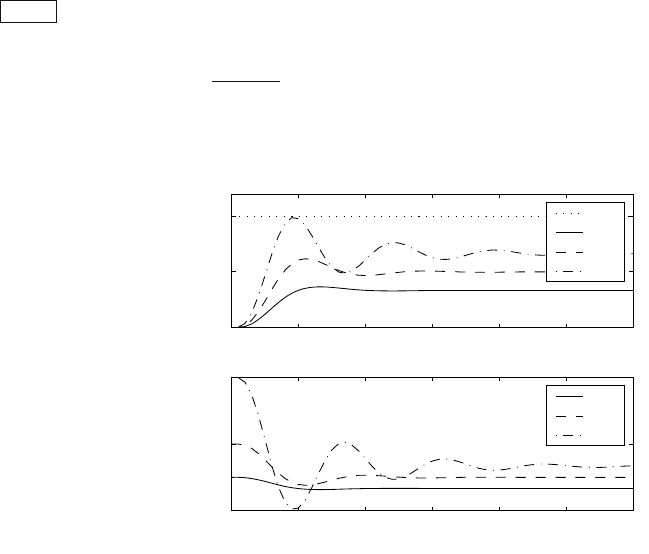
Fig. 7.11 shows simulations with various gains of the controller.

0 5 10 15 20 25 30

0.5

w,y

0.5

0 5 10 15 20 25 30

0.5

Fig. 7.11. Proportional control to the setpoint value w = 1 with various gains Z

of the controller

Simulation results again illustrate typical features of proportional control.

Permanent control error decreases with increasing controller gain. How-

ever, stability indices deteriorate and for a suﬃciently high Z

can the

closed-loop system become instable.

Integral Control

The problem of the steady-state control error is not satisfactorily solved even

with the modiﬁed proportional controller with the shift u

. If the setpoint

changes, it is necessary to ﬁnd a new value of u

. A more appropriate solution

is to introduce a pure integrator – the manipulated variable changes while the

control error is not zero. This can mathematically be deﬁned as

7.4 PID Controller 271

du(t)

e(t) (7.40)

where the constant T

is called integral time constant and determines the

speed of the change of the manipulated variable in the case of the unit control

error. The smaller value T

the larger changes of u are generated.

Historically, the integral action (I controller) was discovered by improving

equation (7.39) where the shift u

was calculated using feedback with the ﬁrst

order ﬁlter with time constant T

(s)=

s +1

U(s) (7.41)

Combining (7.39), (7.41) and eliminating the intermediate variables yields

E(s)=T

(s) ⇔ T

(t)

= Z

e(t) (7.42)

U(s)=

s +1

E(s) ⇔ u(t)=Z



e(t)+



e(τ)dτ



(7.43)

This represents integral action for u

(t) and the PI controller for u(t).

Example 7.7: Heat exchanger control with the PI controller

www

Consider feedback control of the heat exchanger with the PI controller

deﬁned with the transfer function R(s)=Z

[1 + 1/(T

s)].

Transient response of the exchanger to a step change of the disturbance

with magnitude A (setpoint is considered to be zero) in the Laplace trans-

form is given as

Y (s)=

s+1

1+Z

s+1

+(T

+ Z

)s + Z

This function is stable and converges to zero. Some simulations for Z

10 are shown in Fig. 7.12.

The exchanger response to a step change of the setpoint with magnitude

A (disturbance is considered to be zero) in the Laplace transform is

Y (s)=

s +1)

+(T

+ Z

)s + Z

The steady-state control error is given as

e(∞)=w(∞) − y(∞)=A − lim

s→0

sY (s)=A − A =0

We can see that the controller removes the steady-state control error.

Compared to the disturbance transfer function the numerator contains a

stable zero s = −1/T

that ampliﬁes with decreasing value T

and thus

approaches instability. Practical consequence will be increasing overshoot.

Some simulation results are shown for Z

= 10 in Fig. 7.13.

272 7 The Control Problem and Design of Simple Controllers

0 1 2 3 4

−0.02

0.02

0.04

0.06

0.08

0.1

y/AZ

t/T

=0.2

Fig. 7.12. Heat exchanger – distur-

bance rejection with the PI controller

0 1 2 3 4

0.2

0.4

0.6

0.8

1.2

y/A

t/T

=0.2

Fig. 7.13. Heat exchanger – setpoint

tracking with the PI controller

Example 7.8: Higher order system with the PI controller www

Consider again control of a higher order system with the transfer function

of the form

G(s)=

(s +1)

controlled by the PI controller with proportional gain Z

= 1. Fig. 7.14

illustrated eﬀects of changing the integral time constant.

Simulation results demonstrate typical features of PI control. The steady-

state control error is zero, only with a large T

the output variable con-

verges only slowly. On the other side, with the decreasing T

(increasing

integral action) the controller becomes more aggressive and magnitudes of

oscillations increase as well. The closed-loop system can eventually become

instable for a suﬃciently small T

Derivative Control

Derivative action theoretically improves stability of the closed-loop system. P,

I controllers do not inﬂuence the loop instantaneously but only after a certain

time. Derivative controller deﬁned by equation

u(t)=T

de(t)

(7.44)

where T

is derivative constant forecasts the future value of the control error.

This can be shown by using the Taylor expansion of the term e(t + T

)

e(t + T

) ≈ e(t)+T

de(t)

(7.45)

Graphical representation of this equation is shown in Fig. 7.15.

7.4 PID Controller 273

0 5 10 15 20 25 30

0.5

1.5

w,y

0 5 10 15 20 25 30

0.5

1.5

Fig. 7.14. PI control with setpoint w = 1 and several values of T

t+T

e(t+T )

e(t)

e(t)+T

Fig. 7.15. Graphical representation of derivative controller eﬀects

An ideal derivative controller is rather sensitive to noise in the controlled

variable and the derivative action can lead to frequent and large changes of

the manipulated variable. Besides, the ideal derivative action is not realisable

as it is not proper.

This has lead to introduction of a ﬁltered D controller with the transfer

function

R(s)=

(7.46)

This is nothing else than the ideal D controller in series with a ﬁrst order

system with the time constant T

/N . Typical values of N are between 5

and 20.

Example 7.9: Higher order system PID control

www

Consider again control of a higher order system with the transfer function

of the form

274 7 The Control Problem and Design of Simple Controllers

G(s)=

(s +1)

controlled by the PID controller and assume constant parameters Z

3.76, T

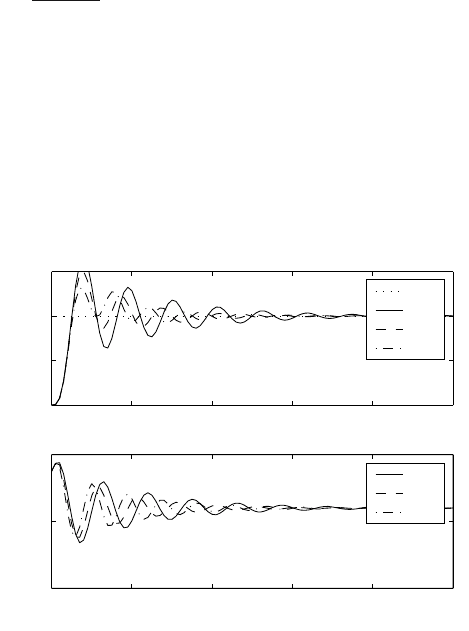
=2.85. Fig. 7.16 shows simulations with diﬀerent values of the

derivative constant.

We can see that the increasing T

improves the speed of control and

overshoot. Theoretically performance should always improve. However,

as the derivative action has predictive behaviour, the presence of noise

inhibits arbitrary increase of T

0 10 20 30 40 50

0.5

1.5

w,y

0.7

1.0

1.4

0 10 20 30 40 50

−5

0.7

1.0

1.4

Fig. 7.16. PD control with setpoint w = 1 and several values of T

Loosely speaking PID controller parameters inﬂuence performance and

stability in the following way:

• increase of P action increases speed and reduces stability,

• increase of I action decreases speed and improves stability,

• increase of D action increases speed and improves stability.

7.4.2 PID Controller Structures

The PID controller contains three components: proportional, integral, and

derivative. Its realisations can be diﬀerent depending on implementation (elec-

trical, pneumatic, electronic, etc.)

Most often the following PID structures are used:

• without interaction

7.4 PID Controller 275

R(s)=Z



+ T



(7.47)

• with interaction (in series)

R(s)=Z





(1 + T

s) (7.48)

• parallel

R(s)=Z

+ T

s (7.49)

It is important to remember that the controller constants are closely tied

to its realisation and that alternative representation results in their diﬀerent

values. Design methods presented in Section 7.4.6 usually assume the structure

without interaction (7.47).

7.4.3 Setpoint Weighting

The standard PID controller processes control error. A more ﬂexible structure

can be deﬁned with a controller of the form

u(t)=Z



(t)+



e(τ)dτ + T

(t)



(7.50)

where modiﬁed P and D variables are deﬁned as

(t)=bw(t) −y(t) (7.51)

(t)=cw(t) −y(t) (7.52)

and b, c are user deﬁned parameters. Both inﬂuence response to an abrupt

change of setpoint w where the traditional PID controller reacts by a step

change of proportional and derivative part. The parameter b controls the

maximum overshoot that is the smallest with b = 0. Field tested values are

between 0.3 −0.8. (see Example 7.15 on page 291). Similarly, the parameter c

can be used to suppress large changes of the manipulated variable caused by

derivative action.

In general, the classical controller described by equations (7.47)–(7.49)

represents a one degree-of-freedom controller that reacts in exactly the same

way to changes in disturbance or setpoint. Often however, closed-loop speci-

ﬁcations are diﬀerent and responses to setpoints and disturbances have to be

speciﬁed independently. In that case a more suitable structure can be that of

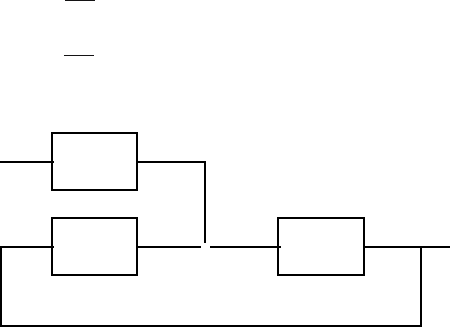
the two degree-of-freedom controller (Fig. 7.17). Here actually two controllers

are used. The feedback part R

deals with the control error and the feed-

forward part R

processes only the setpoint. Their transfer functions can be

speciﬁed as

276 7 The Control Problem and Design of Simple Controllers

= Z



+ T



(7.53)

= Z



b +

+ cT



(7.54)

G(s)

- -

−

Fig. 7.17. Closed-loop system with a two degree-of-freedom controller

7.4.4 Simple Rules for Controller Selection

• Most often the best controller is the simplest, i. e. the proportional con-

troller. It can be used if nonzero steady-state error is acceptable or if the

controlled system contains pure integrator. In process control its typical

use is in pressure control or level control.

• PI controller can be used if the simple proportional action is unaccept-

able and dynamics of the controlled system is simple. Its advantage is the

zero steady-state error but at the price of larger overshoot and oscillatory

behaviour. Moreover, further increase of the controller gain can lead to

instability.

• PD controller – grace to derivative action does not exhibit large overshoot

and settles fairly quickly. However, without integral action, the nonzero

steady-state error results with the same value as that of the P controller.

It is used mainly for processes with integrating behaviour or with large

time constants.

• PID controller is suitable in remaining cases - it is robust, forecasts fu-

ture process behaviour and in general its gain is smaller than that of the

corresponding PI controller. Its drawback is an increased sensitivity to

measurement noise.

• Problematic processes for PID controllers include systems with time delay,

with time variant parameters or oscillatory processes.

7.4 PID Controller 277

7.4.5 Practical Aspects

Integrator Windup and Constraints Handling

Manipulated variables are always limited within the interval (u

min

max

). For

example valves can be somewhere between fully closed and fully open, the

smallest motor speed is zero and the largest is given by its technical parame-

ters, etc.

If a controller contains pure integrator(s) and the manipulated variable

is on the constraint, the state corresponding to the integrator continues to

integrate the control error. Hence, even if the control error sign ﬁnally changes,

the manipulated variable does not change immediately, as the integral part

dominates the controller. Classical symptoms of (integrator windup) are large

overshoots caused by delayed activity of the controller. This phenomenon is

illustrated in the next example.

Example 7.10: Integrator windup

www

Consider again control of a higher order system with the transfer function

of the form

G(s)=

(s +1)

with the PI controller of the form

R(s)=1+

Assume step setpoint change w = 1 and constraints on the input u ∈

0.9, 1.1. Simulation results are shown in Fig. 7.18a. Even if the controlled

output y reaches setpoint at time t = 7, the manipulated variable remains

at the upper constraint up to time t = 20. This implies a larger settling

time. To understand better this phenomenon, state of the integral part is

also shown in the ﬁgure. This variable increases even if the manipulated

variable is on the upper constraint.

Improvement can be observed when feedback procedure described below is

used. The simulation results are shown in Fig. 7.18b. Integrator value de-

creases rapidly and both control and the controlled output react correctly

when constraints are active.

There are several ways how to eliminate or suppress the windup phe-

nomenon. Often, it is caused by a sudden change of the setpoint variable. In

that case it may be possible to change the setpoint smoothly and more slowly

so that the control signal remains within limits.

Another possibility is to use velocity (incremental) algorithms when the

controller generates only changes of the manipulated variable. Of course, if

the manipulated variable hits the constraint, the controller output is zero.

The most commonly used method is the back calculation – if the manip-

ulated variable is out of limits, the integral part is recalculated back so that

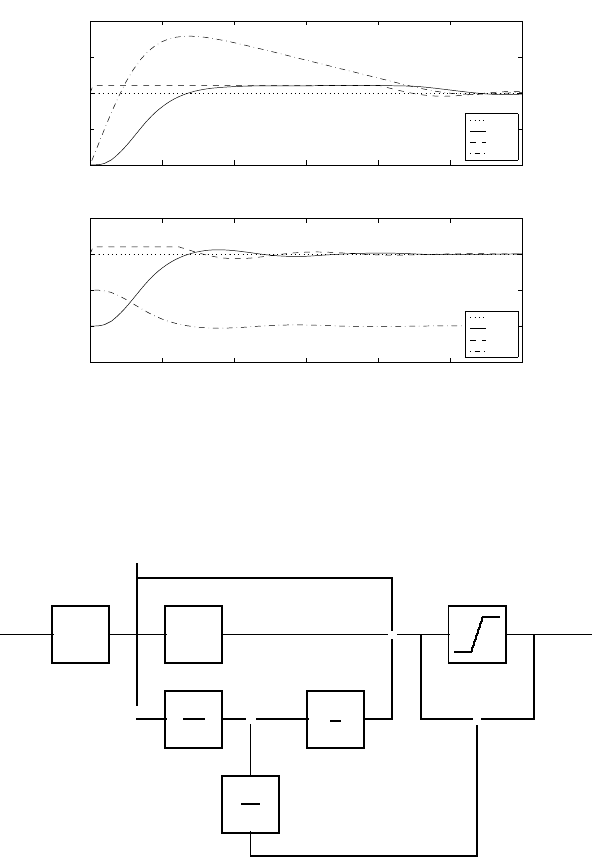
278 7 The Control Problem and Design of Simple Controllers

0 5 10 15 20 25 30

0.5

1.5

(a)

integ

0 5 10 15 20 25 30

−0.5

0.5

1.5

(b)

integ

Fig. 7.18. Windup phenomenon. (a) Problem, (b) Solution

the control signal is on the constraint. In practice however, this is not realised

in each calculation step but dynamically with a time constant T

. The block

scheme of this anti-windup setup is shown in Fig. 7.19.

- - e- - -

- - -

- 

PID

−

Fig. 7.19. Anti-windup controller

The modiﬁcation consists in an additional feedback loop on the input of

which is diﬀerence between calculated and really applied control signal. If the

manipulated variable is within constraints, this error is zero and the original

controller remains. If the error is nonzero, the integral signal is changed until

it is again at the desired value.

7.4 PID Controller 279

The time constant T

speciﬁes speed of the integral rewind. At the ﬁrst

sight it seems that it should be the smallest possible. However, it has been

found that in presence of noise the integrator could interrupt its activity. An

empirical rule of thumb is the value about T

√

Bumpless Transfer

Modern PID controllers can function in automatic and manual modes. The

standard mode is automatic when the controller calculates the control signal.

The manual mode serves to handle nonstandard situations when the control

signal is speciﬁed by process operators. It is important to guarantee that

change between the modes is without undesired transient eﬀects, i. e. the new

mode should start smoothly at the last calculated value of the old mode.

The bumpless transfer problem can be removed if incremental form of con-

trollers is used. In other cases it is possible to use the anti-windup scheme

(Fig. 7.19) where the controller follows the actually applied signal to the

process.

Transient eﬀects can also occur when controller parameters are changed.

In that case it is necessary to recalculate the integral action.

Digital Implementation

The ﬁrst PID controllers were constructed as thecontinuous-time pneumatic or

(later) electric devices. With the recent advances of microprocessors controllers

are mostly implemented digitally as discrete-time algorithms. In general, this

brings many advantages as the microprocessor not only implements the control

law but it can also trigger alarms, ﬁlter input variables, etc. However, there are

some features and properties special to digital devices as such a controller does

not process the analogue signal continuously but only at some time instants

– sampling times.

The most important parameters of a digital device is its sampling period

. If it is chosen too large, some dynamic eﬀects can escape. Practical rule of

thumb is to choose it such that the interval (5 − 10)T

should cover the rise

time of the plant. In the frequency domain this can correspond to 10 times

the bandwidth. If there is no information about the controller process, it is

recommended to choose the sampling time as small as possible. Theoretical

issues on the choice of T

are also discussed in Section 5.1.

The discretisation in itself covers approximation of all three parts of the

PID controller when the original diﬀerential equation is transformed into a

diﬀerence equation.

To derive a digital version of the PID controller assume the parallel form

given by (7.47). Its discrete version can be obtained in various ways. For

example by backward approximation of the derivative and integral parts as