Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

280 7 The Control Problem and Design of Simple Controllers

de(t)

≈

e(kT

) −e((k − 1)T

)



e(τ)dτ ≈ T



i=1

e(T

(i −1)) (7.55)

where the continuous time t has been replaced by its discrete time counterpart

in sampling times kT

,k =0, 1,.... This gives for the control law

u(kT

)=Z

e(kT



i=1

e(T

(i −1)) +

[e(kT

) −e((k − 1)T

)]

(7.56)

Another possibility is to use forward or trapezoidal approximation:



e(τ)dτ ≈ T



i=1

e(iT

) ≈



i=1

[e(iT

) −e((i −1)T

)] (7.57)

If for example forward approximation of the part I is used then digital PID

controller is given as

u(kT

)=Z

e(kT



i=1

e(iT

)) +

[e(kT

) −e((k − 1)T

)]

(7.58)

If the sampling time is suﬃciently small, there are no large diﬀerences between

approximations. Some precaution has to be taken in the case of forward or

trapezoidal transformations when for small values of T

can the approxima-

tions be unstable.

Equation (7.58) is not particularly suitable for practical implementation

as it is necessary to know all values of past control errors. Therefore, recurrent

versions are used that can be obtained by subtracting u in sampling times kT

and (k − 1)T

u(kT

)=Δu(kT

)+u((k − 1)T

) (7.59)

Δu(kT

)=Z



e(kT

)





− e((k −1)T

)





+ e((k −2)T

)



(7.60)

A general form of a digital PID controller can be given as

u(k)=q

e(k)+q

e(k − 1) + q

e(k − 2) + u(k − 1) (7.61)

The corresponding discrete time transfer function is then

R(z

−1

+ q

−1

+ q

−2

1 −z

−1

(7.62)

The presented technique can be used for an arbitrary transformation of a

continuous-time PID controller to a digital form.

7.4 PID Controller 281

7.4.6 Controller Tuning

Analytical Methods

Standard Forms

The method of standard forms belongs to the class of analytical methods where

transfer function of the controlled process is known. Standard forms refer to

some known transfer function structures and coeﬃcients where behaviour of

the closed-loop system is known and optimal in some sense.

Consider the closed-loop system transfer function of the form

(s)=

+ a

n−1

+ ···a

s + a

(7.63)

that can be obtained if the open-loop transfer function contains one pure

integrator and no zeros. Standard forms for this case are:

• Binomial form with a real stable pole s = −ω

with mutiplicity of n

(s)=

(s + ω

)

(7.64)

Diﬀerent system orders n imply the following standard forms

s + ω

+2ω

s + ω

+3ω

s + ω

+4ω

+6ω

+4ω

s + ω

This standard form provides relatively sluggish underdamped transient

responses.

• Butterworth form where the poles are located in the left half of the complex

plane on the semicircle with radius of ω

. Normalised polynomials are then

of the form

s + ω

+1.4ω

s + ω

+2ω

s + ω

+2.6ω

+3.4ω

+2.6ω

s + ω

• Minimual t

– the fastest transient reponse with maximum overshoot of

5%.

s + ω

+1.4ω

s + ω

+1.55ω

+2.10ω

s + ω

+1.60ω

+3.15ω

+2.45ω

s + ω

• Minimum of ITAE cost function.

s + ω

+1.4ω

s + ω

+1.75ω

+2.15ω

s + ω

+2.1ω

+3.4ω

+2.7ω

s + ω

282 7 The Control Problem and Design of Simple Controllers

Binomial form

0 2 4 6 8 10 12 14

0.2

0.4

0.6

0.8

n=1

n=2

n=3

n=4

Butterworth form

0 2 4 6 8 10 12 14

0.2

0.4

0.6

0.8

n=1

n=2

n=3

n=4

Minimal t

0 2 4 6 8 10 12 14

0.2

0.4

0.6

0.8

n=1

n=2

n=3

n=4

Minimum ITAE

0 2 4 6 8 10 12 14

0.2

0.4

0.6

0.8

n=1

n=2

n=3

n=4

Fig. 7.20. Step responses of selected standard transfer functions

The above mentioned standard forms for various system orders and normalised

with respect to ω

lead to step responses shown in Fig. 7.20.

Possible drawbacks of standard forms include a rather strict restriction

on the open-loop system structure. The solution very often leads to a under

or overdetermined system of equations and is practically useless for standard

PID design. On the other side, denominators of standard forms are frequently

used in pole placement control design.

The Naslin Method

Here the controller is designed based on the requirement on the maximum

overshoot. The method considers relations between the coeﬃcients of the

closed-loop denominator (7.63) of the form

= αa

i−1

i+1

(7.65)

where the coeﬃcient α is determined as a function of the desired overshoot

from the table

7.4 PID Controller 283

α 1.7 1.8 1.9 2 2.2 2.4

max

20 12 8 5 3 1

Example 7.11: Naslin method

The controlled system with the transfer function

G(s)=

12s

+8s +1

is subject to unit step disturbance on the system input. Design PI con-

troller using the Naslin method with maximum overshoot of 5%.

The transfer function between the disturbance and the process output in

the closed-loop system can be derived using the block algebra

(s)=

G(s)

1+G(s)R(s)

Assume the PI controller with the structure

R(s)=Z





The closed-loop denominator polynomial is then given as

12s

+8s

+(1+Z

)s +

If the maximum overshoot of 5% is speciﬁed then α = 2 and two equations

can be written

=2a

⇒ (1 + Z

)

=16

=2a

⇒ 64 = 24(1 + Z

)

The resulting controller is then given as

R(s)=



15s



The Strejc Method

To determine parameters of the PID controller of the form

R(s)=Z



+ T



(7.66)

using the Strejc method let us consider the controlled system of the form

F (s)=

(Ts+1)

−T

(7.67)

284 7 The Control Problem and Design of Simple Controllers

where Z is the process gain, T time cosntant, T

time delay, and n the process

order.

The controller parameters can then be read from Table 7.1. If only step

response of the process is known, the transfer function can be estimated using

the Strejc identiﬁcation method described in Section 6.2.3.

We choose a suitable controller structure and read its parameters from

the corresponding row of the table. If PID structure is chosen, the controlled

process has to be at least of the third order. For P and PI controllers the

system order has to be at least two. This follows from the controller gain Z

calculations in Table 7.1.

Table 7.1. Controller tuning using Strejc method

Controller Z

n − 1

n +2

4(n − 1)

n +2

PID

7n +16

16(n − 2)

7n +16

(n +1)(n +3)

7n +16

Example 7.12: The Strejc methodwww

Consider again the controlled process with parameters Z =1,T =1,

n = 4. When PID controller structure is chosen, its parameters calculated

from Table 7.1 are Z

=1.38, T

=2.93, T

=0.80. The simulation

results are shown in Fig. 7.21.

Pole Placement

One drawback of standard forms methods is that the overall transfer function

of the closed-loop system is prescribed. This narrows the applicability of the

method considerably. In pole placement control design only the closed-loop

denominator that determines stabilility is speciﬁed. The advantage of this

approach is its usability for a broad range of systems. On the other side, as

the closed-loop numerator cannot be speciﬁed, it can happen that its zeros

can have impact on performance.

If the controlled system is of the ﬁrst or second order and the controller of

PID structure then the characteristic equation can be one of the following

s + ω

= 0 (7.68)

+2ζω

s + ω

= 0 (7.69)

(s + αω

)(s

+2ζω

s + ω

) = 0 (7.70)

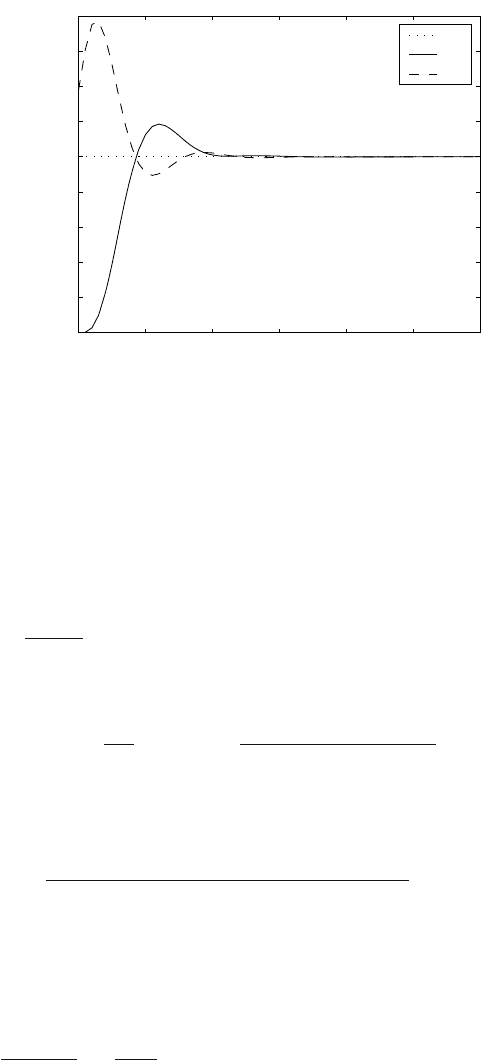
7.4 PID Controller 285

0 5 10 15 20 25 30

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

w,y,u

Fig. 7.21. The PID controller tuned according to Strejc

where ζ is relative damping, ω

natural undamped frequency, and α acoef-

ﬁcient. Specifying suitable values of parameters ζ,ω

,α in (7.68)–(7.70) can

lead to one of the standars forms. If higher order characteristic polynomial is

to be considered, then it is usually taken with the structure of Butterworth

polynomials or some other standard forms.

Consider the controlled system of the ﬁrst order with transfer function

G(s)=

Ts+1

(7.71)

controlled by the PID controller of the form

R(s)=Z



+ T



s +1+T

)

(7.72)

The closed-loop transfer function between the setpoint and output is given by

equation (7.3) as

(s)=

s +1+T

)

(T + ZZ

+(1+ZZ

)s + ZZ

(7.73)

The characteristic equation is of the second degree and thus it is possible to

assign two poles. As the PID controller contains three tunable parameters,

one of them is superﬂuous. Hence, we will in the further consider only the PI

controller structure. In this case the characteristic equation can be written as

1+ZZ

s +

= 0 (7.74)

286 7 The Control Problem and Design of Simple Controllers

To place the poles, the standard characteristic equation (7.69) will be used.

Comparing the coeﬃcients at the corresponding powers of s yields

2ζω

1+ZZ

,ω

(7.75)

Therefore, the controller parameters are given as

2ζω

T − 1

2ζω

T − 1

Tω

(7.76)

The closed-loop system G

numerator contains a stable zero s = −1/T

If the integrating time constant is large, this zero is located near unstable

region and can have impact on overshoot. To prevent this is is recommended

either to lower the time constant or to use the two degree-of-freedom controller

structure and weigh the setpoint inﬂuence by the parameter b (see (7.50)).

Example 7.13: Pole placement design for a heat exchanger

www

Let us consider minimisation of the ITAE performance index with require-

ment that the controlled output reaches the setpoint at T

100%

=0.5 min.

We assume the heat exchanger time constant T = 1 min and the gain

Z =1.

Comparing the second order standard ITAE polynomial with equa-

tion (7.69) gives the value of ζ =0.7. The corresponding normalised step

response speciﬁes for time T

100%

relation ω

100%

=3.1, hence ω

=6.2.

The controller parameters are then

=7.68,T

=0.2

Simulation of the closed-loop system is shown in Fig. 7.22. It can be no-

ticed that requirements on the closed-loop system were not exactly met

as T

100%

is smaller than speciﬁed. This is caused by the fact that the nu-

merator is not constant but the ﬁrst order polynomial. Smaller overshoot

and thus larger T

100%

can be achieved by modiﬁcation of the controller

with the parameter b.

Let us now consider the pole placement design for a second order system

with the transfer function of the form

G(s)=

s + b

+ a

s + a

(7.77)

controlled by the PID controller

R(s)=Z



+ T



s +1+T

)

(7.78)

The closed-loop transfer function between the setpoint and output is given as

(s)=

s +1+T

)(b

s + b

)

s(s

+ a

s + a

s +1+T

)(b

s + b

)

(7.79)

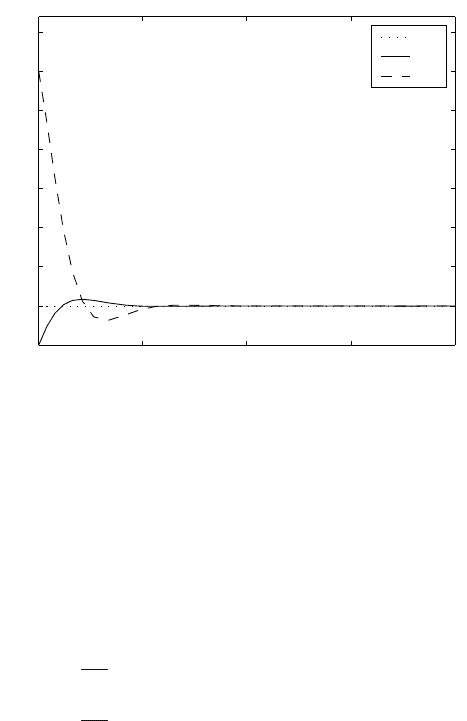
7.4 PID Controller 287

0 1 2 3 4

w,y,u

Fig. 7.22. Heat exchanger control using pole placement design

The characteristic equation is of the third order. Hence, it is possible to choose

three poles. As the PID controller has three tunable parameters, it is suitable

for this system. We can use the standard characteristic equation (7.70) with

three parameters that specify an arbitrary type of the standard forms.

Comparing the coeﬃcients at the corresponding powers of s yields the

system of equations with three unknowns – controller parameters

+ b

= ω

(α +2ζ)(1 + b

)=c

(1 + b

)(7.80)

+ b

= ω

(1 + 2αζ)(1 + b

)=c

(1 + b

)(7.81)

= ω

α(1 + b

)=c

(1 + b

) (7.82)

The equations are nonlinear as they contain multiplication and division of

unknown variables. If a substitution with

= Z

will be

introduced, a system of linear equations with unknown variables Z

will be obtained

⎛

⎝

− c

−c

0 −c

⎞

⎠

⎛

⎝

⎞

⎠

⎛

⎝

− a

⎞

⎠

(7.83)

Solution of the equations and backsubstitution yield the controller parameters.

Experimental Methods

All analytical methods assume knowledge of the process transfer function.

As this is rarely precisely known, the methods can be used only for the ﬁrst

288 7 The Control Problem and Design of Simple Controllers

estimate of the controller parameters. Next, these are applied to the process

and manually retuned to yield the desired performance.

These drawbacks can partially be eliminated by using experimental meth-

ods that explore dynamic properites of the controlled process to ﬁnd controller

parameters.

Trial-and-Error Method

A typical tuning of PID controller parameters can be as follows:

• Integral and derivative actions are turned oﬀ (T

is on maximum, T

zero) so that only proportional action with small controller gain results.

• The proportional gain is gradually increased until permanent oscillations

result (undamped behaviour). A care has to be taken so that the manip-

ulated variable is not on the constraints.

• The proportional gain is reduced to a half.

• Integral time constant is gradually reduced until again permanent oscilla-

tions occur. T

is then set to 3T

I,crit

• Derivative action is increased until again permanent oscillations occur. T

is then set to a third of the critical value.

The method cannot always be used as permanent oscillations can compromise

the safety of the technology. In any case these steps indicate inﬂuence of each

controller part and their relation to controller tuning.

Ziegler-Nichols Methods

These are among the most used and widely spread methods for PID controller

tuning that have been in use since 1950. The derivation is based on the ﬁrst

order controlled system with time delay and the controller parameters are

optimised for underdamped transient response with the damping coeﬃcient of

about 25%. The procedure can either be applied using permanent oscillations

or is based on the step response. The method of permanent oscillations is in

fact only a modiﬁcation of the trial-and-error method.

Method of Permanent Oscillations The controller is at ﬁrst set up only with

a proportional action and its gain is increased until permanent oscillations

occur. The closed-loop system is only marginally stable at this point. Criti-

cal proportional gain Z

amd critical time period of the oscillations T

are

obtained. These values are used for a given controller structure for the calcu-

lation of its parameters from Table 7.2. Several settings are given in the table

– the usual Ziegler-Nichols settings as well as the settings for more robust

controller with a smaller or zero overshoot.

Another possibility of getting permanent oscillations in the closed-loop

system can be realised using a relay with hysteresis. In this case the process

input is of rectangular shape. The advantage is that the output magnitude

can be tuned. The relay output changes every time the control error changes

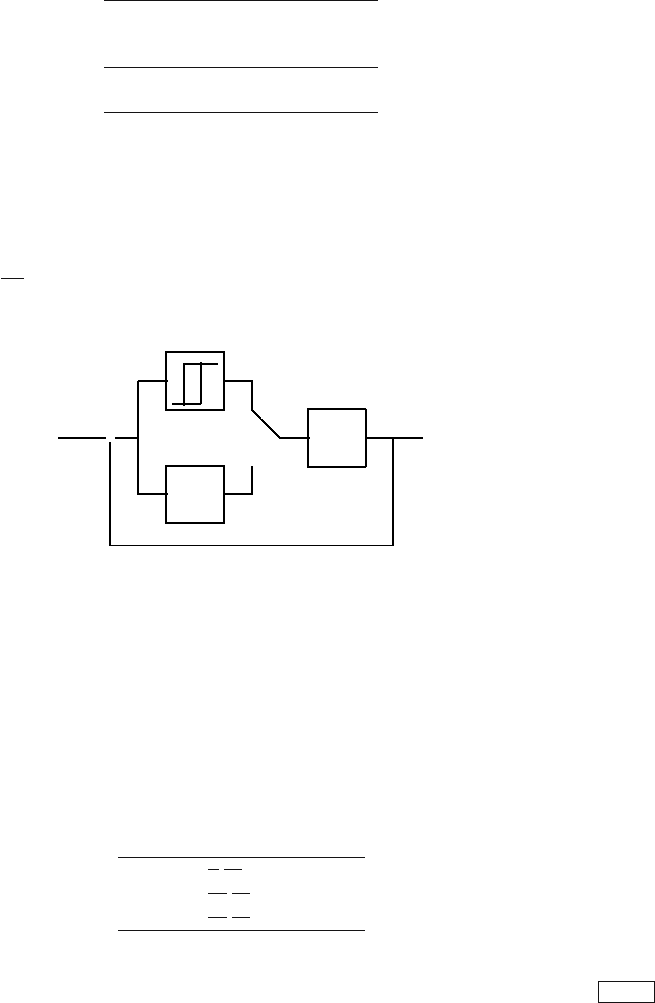
7.4 PID Controller 289

Table 7.2. Ziegler-Nichols controller tuning based on permanent oscillations. PID

sets smaller overshoot, PID

is underdamped

Regul´ator Z

P0.5Z

PI 0.4Z

0.8T

PID 0.6Z

0.5T

0.125T

PID

0.33Z

0.5T

PID

0.2Z

0.5T

sign (Fig. 7.23). After a certain time the oscillations settle and it is possible

to ﬁnd out the value of T

. If we consider the magnitude of the input ±u

and the magnitude of the output ±y then it follows the theory of harmonic

equilibrium that the critical controller gain is given as

πy

(7.84)

PID

G(s)

- -

−

Fig. 7.23. Closed-Loop system with a relay

Step Response Method Often it is not possible to ﬁnd the critical gain of the

controller for safety reasons. In this case it can be easier to measure a step

response of the process and to calculate the controller parameters from it using

Table 7.3. Note that it is not necessary to measure the whole step response,

only the values T

and Z/T

given from the slope of the curve in the inﬂexion

point.

Table 7.3. The Ziegler-Nichols controller tuning based on the process step response

Regul´ator Z

0.9

3.33T

PID

1.2

0.5T

Example 7.14: The Ziegler-Nichols method www