Михайлов В.П., Гущин А.К. Уравнения математической физики. Дополнительные главы

Подождите немного. Документ загружается.

Математический институт им. В. А. Стеклова

Российской академии наук

Лекционные курсы НОЦ

Выпуск 7

Издание выходит с 2006 года

В. П. Михайлов, А. К. Гущин

Дополнительные главы курса

“Уравнения математической физики”

Москва

2007

УДК 517.95

ББК (В)22.311

Л43

Редакционный совет:

С.И. Адян, Д. В. Аносов, О. В. Бесов, И.В. Волович,

А.М. Зубков, А. Д. Изаак (ответственный секретарь),

А.А. Карацуба, В.В. Козлов, С.П. Новиков,

В.П. Павлов (заместитель главного редактора),

А.Н. Паршин, Ю. В. Прохоров, А.Г. Сергеев, А.А. Славнов,

Д.В. Трещев (главный редактор), Е.М. Чирка

Л43 Лекционные курсы НОЦ / Математический инсти-

тут им. В. А. Стеклова РАН (МИАН). – М.: МИАН, 2007.

Вып. 7: Дополнительные главы курса “Уравнения математи-

ческой физики” / Михайлов В. П., Гущин А. К. – 146 с.

ISBN 5-98419-022-2

Серия “Лекционные курсы НОЦ” – рецензируемое продолжающееся

издание Математического института им. В. А. Стеклова РАН. В серии

“Лекционные курсы НОЦ” публикуются материалы специальных кур-

сов, прочитанных в Математическом институте им. В. А. Стеклова Рос-

сийской академии наук в рамках программы Научно-образовательный

центр МИАН.

Настоящая брошюра содержит лекции дополнительные главы кур-

са “Уравнения математической физики”, прочитанные в осеннем семест-

ре 2006-го года.

ISBN 5-98419-022-2

 Математический институт

им. В. А. Стеклова РАН, 2007

 Михайлов В. П., Гущин А. К., 2007

Оглавление

Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Часть I 7

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Глава 1. Пространства Соболева

и теоремы вложения 13

§ 1. Обобщенные производные

и усредненные функции . . . . . . . . . . . . . . . . . . 17

§ 2. Пространства Соболева . . . . . . . . . . . . . . . . . . 22

§ 3. След функций из H

(Q) . . . . . . . . . . . . . . . . . . 25

§ 4. Пространство

(Q) . . . . . . . . . . . . . . . . . . . . 30

§ 5. Вложение H

(a, b) в C([a, b]) . . . . . . . . . . . . . . . 32

§ 6. Вложение H

(Q) в L

(Q) . . . . . . . . . . . . . . . . . 34

§ 7. Компактность вложения H

(Q) в L

(∂Q) . . . . . . . . 37

§ 8. Вложение H

(Q) в C

(

Q ) . . . . . . . . . . . . . . . . . 40

§ 9. Эквивалентные нормировки пространств H

(Q) и

(Q) 46

Глава 2. Краевые задачи

для эллиптических уравнений 51

§ 1. Вторая и третья краевые задачи

для уравнения второго порядка . . . . . . . . . . . . . . 51

§ 2. Первая краевая задача

для уравнения второго порядка . . . . . . . . . . . . . . 63

§ 3. Задача о собственных значениях

и собственных функциях . . . . . . . . . . . . . . . . . . 75

Часть II 83

Глава 3. Некоторые дополнительные сведения

из теории пространств Соболева 85

§ 1. Пространства L

и L

∞

. . . . . . . . . . . . . . . . . . . 85

§ 2. Вложение пространства W

(Q) в L

(Q) . . . . . . . . . 89

§ 3. Обобщенные производные

сложной функции . . . . . . . . . . . . . . . . . . . . . . 97

Глава 4. Разрешимость задачи Дирихле

для общего линейного эллиптического

уравнения второго порядка 103

§ 1. Принцип максимума . . . . . . . . . . . . . . . . . . . . 104

§ 2. Пространства

−1

(Q) и W

−1

(Q) . . . . . . . . . . . . . 110

§ 3. Теоремы об однозначной разрешимости

задачи Дирихле . . . . . . . . . . . . . . . . . . . . . . . 118

Глава 5. Непрерывность по Гёльдеру

решений эллиптических уравнений 125

§ 1. Субрешения эллиптического уравнения . . . . . . . . . 126

§ 2. Локальная ограниченность

обобщенных решений

эллиптического уравнения . . . . . . . . . . . . . . . . . 133

§ 3. Слабое неравенство Гарнака . . . . . . . . . . . . . . . 136

§ 4. Непрерывность по Гёльдеру

решений эллиптического уравнения . . . . . . . . . . . 141

Предисловие

Настоящий курс лекций был прочитан в Научно-образова-

тельном центре при Математическом институте им. В. А. Стек-

лова. Он содержит независимое изложение некоторых разделов

теории линейных эллиптических уравнений второго порядка, не

входящиx в традиционные курсы. Предполагается, что читате-

ли знакомы с основными понятиями и утверждениями функцио-

нального анализа. Изложение базируется на вариационном под-

ходе к рассматриваемым вопросам и концепции обобщенного ре-

шения.

Курс состоит из двух частей. Первая часть – она содержит

лекции, прочитанные В. П. Михайловым, – посвящена разреши-

мости основных краевых задач и необходимым для этого поня-

тиям и утверждениям из теории пространств Соболева. Боль-

шое внимание уделено теоремам вложения и связи обобщенных

решений с классическими. Вторая часть лекций, в которых об-

суждаются более специальные свойства обобщенных решений,

была прочитана А. К. Гущиным. Основной ее целью является

доказательство фундаментального результата Е. Де Джорджи и

Дж. Нэша о гёльдеровой непрерывности решений уравнения с из-

меримыми и ограниченными коэффициентами. Потребности это-

го доказательства во многом определили содержание второй ча-

сти.

Часть I

Введение

Наш курс посвящен обобщенным решениям простейших кра-

евых задач для линейных эллиптических дифференциальных

уравнений второго порядка. В качестве введения рассмотрим

классическую задачу о равновесии мембраны. Мы покажем, что

функция, задающая уравнение мембраны в состоянии равнове-

сия, является обобщенным решением некоторой краевой задачи

для эллиптического уравнения – уравнения Эйлера для квад-

ратичного функционала, представляющего собой потенциальную

энергию мембраны.

Напомним, что мембрана – это тонкая пленка, сопротивля-

ющаяся растяжению; будем представлять ее в виде поверхности

в R

: u = u(x), x ∈ Q, где Q – некоторая ограниченная область

в R

, u(x) ∈ C

( Q ). Считаем, что точки мембраны, находящейся

под действием некоторой системы сил, совершают только вер-

тикальные перемещения, и все силы, приложенные к мембране,

имеют только вертикальные составляющие.

Пусть в точках x ∈ Q на мембрану действует сила с плотно-

стью f(x) − a(x)u, x ∈ Q, а в точках x ∈ ∂Q сила с (линейной)

плотностью f

(x) − a

(x)u, x ∈ ∂Q, т.е. на мембрану действуют

внешние силы с плотностью f (x) для x ∈ Q и f

(x) для x ∈ ∂Q,

и силы сопротивления упругих сред, в которых находится внут-

ренность мембраны (x ∈ Q) и ее граница (x ∈ ∂Q) с плотностя-

ми −a(x)u в области Q и −a

(x)u на границе ∂Q, пропорциональ-

ные величине перемещения мембраны и обратные ему по знаку,

a(x) > 0, x ∈ Q, a

(x) > 0, x ∈ ∂Q – коэффициенты упругости

соответствующих сред.

Работа этих сил по перемещению мембраны из какого-то по-

ложения u = u

(x) в положение u = u(x) соответственно равны

u(x)

(x)



f(x) − a(x)u



du dx



f(x)



u(x) − u

(x)



−

a(x)



(x) − u

(x)





dx,

∂Q



(x)



u(x) − u

(x)



−

(x)



(x) − u

(x)





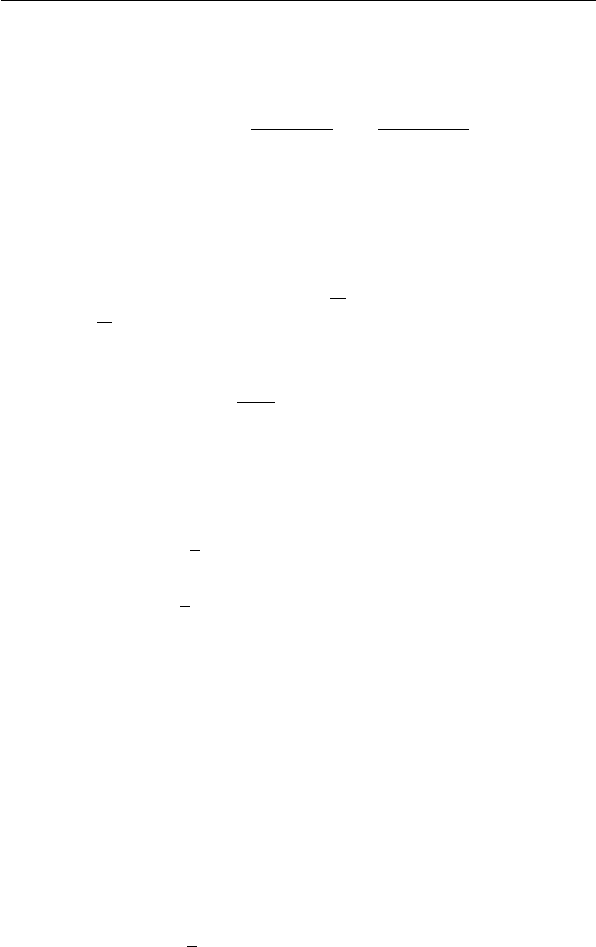
8 Введение

Во внутренних точках x ∈ Q на мембрану действует также

внутренняя упругая сила. Будем считать, что ее работа по пере-

мещению мембраны из положения u

(x) в положение u(x) равна

= −

k(x)



1 + |∇u|

−

1 + |∇u



(работа этой силы, отнесенная к площадке dx = dx

пропор-

циональна изменению площади мембраны, проектирующейся на

эту площадку, с коэффициентом пропорциональности k(x) > 0,

который называется коэффициентом натяжения мембраны). Для

упрощения задачи будем считать, что для всех допустимых поло-

жений мембраны функция |∇u|, x ∈ Q, столь мала, что величиной

|∇u|

, x ∈ Q, можно пренебречь. В таком случае можно считать,

что работа внутренней упругой силы равна

= −

k(x)



|∇u|

− |∇u



dx.

Таким образом, потенциальная энергия мембраны U(u) в по-

ложении u(x) равна

U(u) = U(u

) − T

− T

= C



k(x)|∇u|

+ a(x)u

− 2f(x)u



∂Q



(x)u

− 2f

(x)u



dS,

где U (u

) – потенциальная энергия мембраны в положении u

(x),

а C

– не зависящая от u(x) постоянная.

В рассмотренном случае на значения функции u(x) на грани-

це ограничений не налагается; это случай со свободной границей.

Наряду с ним важным является также случай, когда граница за-

креплена, т.е. когда при всех допустимых u(x) выполняется усло-

вие

u(x)



∂Q

= ϕ(x), (1)

где ϕ(x) – заданная на ∂Q функция (граница мембраны проходит

через пространственную кривую u = ϕ(x), x ∈ ∂Q). В этом случае

потенциальная энергия мембраны в положении u(x) имеет вид

U(u) = C



k(x)|∇u|

+ a(x)u

− 2f(x)u



dx,

где C

– не зависящая от u(x) постоянная.

Введение 9

Согласно принципу механики в состоянии равновесия мем-

браны ее потенциальная энергия минимальна, т.е. в случае сво-

бодной границы характеризующая состояние равновесия функция

u(x) ∈ C

( Q ) реализует минимальное значение функционала

(u) =



k(x)|∇u|

+ a(x)u

− 2f(x)u



∂Q



(x)u

− 2f

(x)u



dS, (2)

среди всех функций из C

( Q ), а в случае закрепленной границы –

минимальное значение функционала

(u) =



k(x)|∇u|

+ a(x)u

− 2f(x)u



dx, (3)

среди всех функций из C

( Q ), удовлетворяющих условию (1).

Здесь мы не будем заниматься вопросом о существовании

функции u(x); ниже существование и единственность решений

каждой из этих задач будут установлены в значительно более об-

щей ситуации.

Пусть функция u(x) ∈ C

( Q ) удовлетворяет условию (1) и ре-

ализует минимальное значение функционала (3) на множестве

функций из C

( Q ), удовлетворяющих условию (1). Тогда при

любой функции v(x) ∈ C

( Q ), удовлетворяющей условию



∂Q

= 0, (1

)

для всех t ∈ R

имеет место неравенство

(t) = J

(u + tv) − J

(u) = 2t



k(x)(∇u, ∇v) + auv − f v



+ t



k(x)|∇v|

+ av



dx > 0, (4)

и следовательно,



k(x)(∇u, ∇v) + auv − f v



dx = 0 (5)

для всех v ∈ C

( Q ), удовлетворяющих условию (1

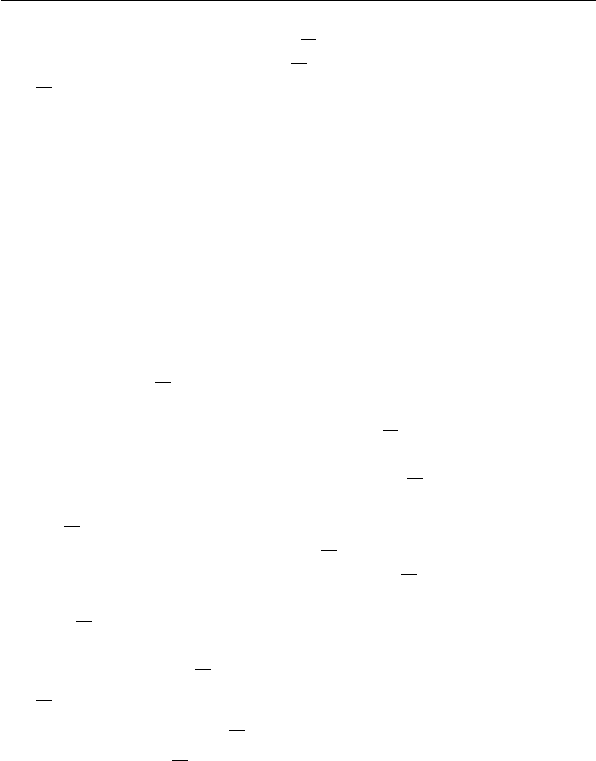
10 Введение

Аналогично, если u(x) ∈ C

( Q ) и реализует минимум функ-

ционала (2) на множестве C

( Q ), то при любой функции v ∈

( Q ) при всех t ∈ R

имеет место неравенство

(t) = J

(u + tv) − J

(u)

= 2t





k(x)(∇u, ∇v) + auv − f v



dx +

∂Q

uv − f

v) dS



+ t





k(x)|∇v|

+ av



dx +

∂Q



> 0,

и следовательно,



k(x)(∇u, ∇v) + auv − f v



dx +

∂Q

uv − f

v) dS = 0 (6)

для всех v ∈ C

( Q ).

Верны и обратные утверждения: если подчиненная гранич-

ному условию (1) и принадлежащая C

( Q ) функция u(x), удо-

влетворяет интегральному тождеству (5) при всех подчиненных

граничному условию (1

) функциях v из C

( Q ), то она реализует

минимальное значение функционала (3) на множестве функций

из C

( Q ), удовлетворяющих граничному условию (1). И анало-

гично, если функция u(x) из C

( Q ) удовлетворяет интеграль-

ному тождеству (6) при любой v из C

( Q ), то она реализу-

ет минимальное значение функционала (2) на множестве функ-

ций C

( Q ). Докажем первое из них, второе доказывается анало-

гично.

Пусть u(x) ∈ C

( Q ), u



∂Q

= ϕ, и выполняется при всех v ∈

( Q ), v



∂Q

= 0, интегральное тождество (5), а w(x) – произ-

вольная функция из C

( Q ), w



∂Q

= ϕ. Пусть v(x) = w(x) −u(x).

Очевидно, v ∈ C

( Q ), v



∂Q

= 0. В силу (4) имеем неравенство

(w) − J

(u) =



(u + tv) − J

(u)





t=1

= 2



k(x)(∇u, ∇v) + auv − f v



dx +



k(x)|∇v|

+ av





k(x)|∇v|

+ av



dx > 0,

из которого вытекает, что J

(w) > J

(u), что и требовалось уста-

новить.