Метлушко К.С. Теория анализа хозяйственной деятельности
Подождите немного. Документ загружается.

однородность заключается в отсутствии таких наблюдений, которые
значительно (аномально) отличаются от основной массы данных.
Критерием однородности информации служит
среднеквадратическое отклонение и коэффициент вариации, которые
рассчитываются по каждому факторному и результативному
показателю. Среднеквадратическое отклонение показывает
абсолютное отклонение индивидуальных значений от
среднеарифметической, а коэффициент вариации характеризует
относительную меру отклонения отдельных значений от
среднеарифметической. Причем, чем больше коэффициент
вариации, тем относительно больший разброс данных в
совокупности.
Изменчивость вариационного ряда принято считать:
- незначительной, если вариация не превышает 10%;
- средней, если вариация составляет 10-20% ;
- значительной, если она больше 20%, но не превышает 33%. Если
вариация больше 33 %, то следует исключить из выборки
нетипичные наблюдения.
3. На третьем этапе осуществляется моделирование связей
между факторами и результативным признаком, т.е. решается вопрос
о выборе формы связи.
На основе экономического и логического анализа природы и
сущности изучаемого явления подбирается тип математического
уравнения, которое наилучшим образом отражает характер
изучаемых зависимостей.
Обоснование уравнения связи проводится с помощью
группировки данных, построения графика и т.д.
Размещение точек на графике показывает, какая зависимость
образовалась: прямолинейная или криволинейная.
Для парной корреляции прямолинейную зависимость описывает
уравнение прямой
у = a
o
+ a
1
x
1,
а для множественной корреляции – уравнение линейной функции
у = а
о
+ а
1
х
1
+ а
2
х
2
+ … + а
n
х
n,
где у – результативный показатель ;
а
о
– постоянная величина, которая не связана с изменением
факторов ;
41
аi - коэффициенты при переменных в уравнении регрессии;
хi - факторные показатели (переменные).
Криволинейные зависимости в экономических исследованиях
встречаются реже. Они могут быть описаны уравнением
- параболы (у = а + bх + сх ²);
- гиперболы (у = а + b/х);
- степенной, показательной и других функций.
Например, при увеличении возраста рабочих до определенного
уровня наблюдается рост их производительности, а затем ее
снижение. Такая зависимость может быть описана уравнением
параболы второго порядка:
у = а + bх + сх².
В случаях, когда трудно обосновать форму зависимости, решение
задачи можно провести по разным моделям и сравнить полученные
результаты. Наилучший вариант выбирается после оценки их по
специальным критериям.
4. На четвертом этапе проводится расчет численных значений
параметров регрессионного уравнения. Он осуществляется методом
наименьших квадратов, при котором в случае прямолинейной
зависимости прямая на графике пройдет наиболее близко к точкам
фактических наблюдений. Для того решается система нормальных
уравнений.
Построение уравнения регрессии проходит шаговым способом.
При этом существуют два варианта:
а) сначала в расчет принимается один фактор, который является
наиболее значимым, потом добавляется второй, третий и т.д. На
каждом шаге рассчитываются уравнение связи, множественный
коэффициент корреляции, коэффициент детерминации и
статистические показатели, характеризующие надежность уравнения
связи. Чем выше величины коэффициентов корреляции и лучше
статистические характеристики, тем точнее уравнение связи
описывает изучаемые зависимости. Если добавление новых факторов
не улучшает оценочные показатели, то их надо отбросить и
остановиться на том уравнении, где эти показатели наиболее
оптимальны.
б) при втором варианте решение модели происходит в обратном
порядке путем последовательного исключения наименее значимых
факторов.
42
5. На пятом этапе дается статистическая оценка уравнения связи
и экономическая интерпретация результатов корреляционного
анализа.
5.4. Показатели оценки уравнения связи и экономическая
интерпретация результатов корреляционного анализа.
Показатели корреляции и регрессии, рассчитанные для
определенного количества наблюдений, могут быть искажены
действием случайных факторов. Для оценки надежности уравнения
связи используют следующие критерии:
- критерий Стьюдента (t);
- критерий Фишера (F);
- средняя ошибка аппроксимации;
- коэффициенты множественной корреляции и детерминации.
Как уже отмечалось, эти показатели рассчитываются на каждом
шаге построения уравнения регрессии.
Для оценки значимости коэффициентов корреляции используется
t- критерий Стьюдента. При этом для каждого коэффициента
расчетное значение t-критерия сравнивается с табличным, которое
находится по таблице значений критериев Стьюдента. Если
расчетное значение выше табличного, то величина коэффициента
корреляции является значимой, а изучаемая связь между
результативным показателем и факторами надежной. Также t-
критерий Стьюдента используется для оценки значимости
параметров уравнения регрессии. В этом случае его расчет
проводится по другим формулам, а выводы делаются аналогично
предыдущим.
Значимость и существенность регрессионного уравнения
оценивается с помощью F-критерия Фишера, определяемого
отношением общей дисперсии к остаточной. Для этого фактическая
(рассчитанная) величина F-критерия сравнивается с табличной.
Табличное значение определяется для принятого уровня значимости
α (обычно α = 0,05) и количестве степеней свободы, которое
рассчитывают по формуле
(m-1)/(n-m),
где m - количество параметров в уравнении связи (вместе с «y»);
n - количество наблюдений.
43
Если F-критерий фактический больше F-критерия табличного, то
уравнение регрессии значимо, а связь между изучаемым показателем
и факторами существенна.
Средняя ошибка аппроксимации используется для статистической
оценки точности уравнения связи и характеризует степень
совпадения фактических (наблюдаемых) и расчетных значений
результативного показателя.
Чем меньше теоретическая линия регрессии, рассчитанная по
уравнению, отклоняется от фактической (эмпиричной), тем меньше
средняя ошибка аппроксимации. В экономических расчетах
допускается погрешность до 5-8%. Тогда в этом случае исследуемое
уравнение связи довольно точно описывает изучаемые зависимости.
Полноту связи характеризуют:
а) множественный коэффициент корреляции, отражающий
тесноту связи или силу совместного воздействия факторов на
величину «y»;
б) коэффициент детерминации, равный квадрату коэффициента
корреляции. Он показывает на сколько процентов вариация
результативного показателя зависит от изменения выбранных
факторов.
После того, как уравнение связи признано надежным, адекватным,
а связь между изучаемым показателем и факторами достаточно
тесной и полной, можно приступать к интерпретации результатов
корреляционного анализа, т.е. их объяснению.
1. В линейной модели коэффициенты при переменных в
уравнении связи показывают, на сколько единиц собственного
измерения изменяется функция при увеличении факторного
показателя на единицу собственного измерения при неизменных
значениях остальных аргументов.
2. Переменные в уравнении регрессии имеют разные единицы
измерения, что делает их несопоставимыми с точки зрения степени
воздействия факторов на результативный показатель. Чтобы
привести их в сопоставимый вид рассчитываются
стандартизированные коэффициенты регрессии или ß -
коэффициенты.
ß-коэффициент показывает, на сколько средних квадратических
отклонений изменится функция с увеличением фактора на одно
среднеквадратическое отклонение.
44

По абсолютной величине ß - коэффициентов можно судить в
какой последовательности находятся факторы по степени их
воздействия на функцию.
3. С этой же целью рассчитываются и коэффициенты
эластичности, которые позволяют провести анализ в процентном
измерении. Коэффициент эластичности показывает, на сколько
процентов в среднем изменится функция с ростом фактора на 1
процент при фиксированных значениях других факторов.
Лекция 2
5.5. Методика применения корреляционного анализа.
5.6. Линейное программирования и область его применения в
анализе.
5.7. Теория массового обслуживания и ее применение в анализе.
5.5. Методика применения корреляционного анализа.
Многофакторный корреляционный анализ играет важную роль в
экономических исследованиях, так как позволяет:
1) изучить закономерности изменения результативного показателя в
зависимости от разных факторов;
2) определить уровень внутрихозяйственных резервов;
3) спрогнозировать уровень изучаемого показателя.
Для определения резервов увеличения или снижения изучаемого
экономического показателя за счет i-го фактора величина изменения
этого фактора умножается на соответствующий ему коэффициент в
уравнении регрессии (с его знаком).
∆у(х
i
)=a
i
×∆x
i
,
где а
i
- коэффициент в уравнении регрессии при i-м факторе;
x
i
- отклонение i-го фактора.
При прогнозировании величины результативного показателя в
уравнение связи подставляют плановые (прогнозируемые) значения
факторных показателей. При этом
предполагается, что форма взаимосвязи будет неизменной на весь
период прогнозирования.
Рассмотрим последовательность применения корреляционного
анализа на конкретном примере.
45

Необходимо провести корреляционный анализ уровня
рентабельности продукции предприятия по данным за 3 года, т.е. за
36 месяцев.
На основе предварительного анализа были отобраны следующие
факторы:
1
х
- материалоотдача, руб.;
2
х
- фондоотдача, руб.;
3
х
- среднегодовая выработка 1 работника, млн.руб.;
4
х
- период оборота оборотных активов, дни;
5
х
- удельный вес продукции высшей категории качества, %.
Информация о рентабельности и выбранных факторах была
собрана за 36 месяцев, что соответствует требованию необходимого
объема выборки данных.
Проверка информации на соответствие закону нормального
распределения показала, что она соответствует требуемым
критериям.
Изучение взаимосвязей между уровнем рентабельности и
факторами показало, что все зависимости имеют прямолинейный
характер, поэтому для уравнения связи была выбрана линейная
функция.
Решение задачи корреляционного анализа проводилось на
компьютере по типовым программам. Исходные данные были
представлены в матричной форме и введены в компьютер. Расчет
проводился шаговым способом с добавлением на каждом шаге
46

нового фактора и оценкой всех статистических характеристик
коэффициентов корреляции и уравнения связи.
В результате на пятом шаге было получено уравнение регрессии:
У = 0,49+3,65
1
х
+0,09×
2
х
+1,02×
3
х
-0,122×
4
х
+0,052×
5
х
.
Значения β– коэффициентов составили:
0,359; 0,275; 0,213; -0,118; 0,133;
Значения коэффициентов эластичности составили:
0,374; 0,308; 0,318; -0,080; 0,001.
Прежде, чем преступить к анализу полученных результатов и их
практическому применению, необходимо убедиться в надежности
уравнения связи.
Величина F-критерия Фишера, равная 95,67, оказалась выше
табличного значения, следовательно, уравнение регрессии значимо.
Средняя ошибка аппроксимации составила 3,64 % , что допустимо
в экономических исследованиях, поэтому, полученное уравнение
связи довольно точно описывает изучаемые зависимости.
Множественный коэффициент корреляции составил 0,92, что
характеризует связь между уровнем рентабельности и выбранными
факторами как достаточно тесную.
Коэффициент детерминации составил 0,85. Это значит, что
вариация рентабельности на 85% зависит от изменения выбранных
факторов, а на долю неучтенных факторов приходится 15%. Таким
образом, данное уравнение регрессии может быть использовано в
практических целях.
Для этого дадим интерпретацию результатов корреляционного
анализа.
1. Коэффициент при переменной X₁ в уравнении регрессии
показывает, что при увеличении материалоотдачи на 1 рубль
рентабельность продукции возрастет на 3,65 процентных пункта. При
увеличении фондоотдачи на 1 рубль рентабельность возрастет на
0,09 процентных пункта.
Однако при увеличении периода оборота оборотных активов на 1
день рентабельность снизится на 0,122 процентных пункта.
2. Объясним
–коэффициенты. При увеличении
материалоотдачи на 1 среднеквадратическое уровень рентабельности
возрастет на 0,359 среднеквадратических.
47

Аналогично объясняются остальные β–коэффициенты. При этом
по степени воздействия на уровень рентабельности факторы
располагаются в следующем порядке:
1
х
,
2
х
,
3
х
,
4
х
,
5
х
,
4
х
.
3. Объясним коэффициенты эластичности. При увеличении
материалоотдачи на 1 % уровень рентабельности возрастет на
0,374%. И так далее.
4. Подсчет резервов. Предположим, что в результате анализа
эффективности использования основных средств было выявлено, что
из-за частых поломок оборудования и несвоевременного его ремонта
фактическая фондоотдача оказалась ниже плановой на 0,13 рубля.
Определим резерв повышения рентабельности продукции за счет
доведения фондоотдачи до планового уровня путем устранения
выявленных недостатков (
Р(х
2
)):
∆P(х₂) = 0,13×0,09 = 0,012 (процентных пункта).
5. Прогнозирование. Предположим, что в результате анализа были
выявлены резервы и предложены меры, реализация которых позволит
повысить эффективность использования производственных ресурсов,
улучшить качество продукции и ускорить оборот оборотных активов.
Проведенные расчеты позволили определить возможное
изменение факторов, включенных в уравнение связи. Необходимо
спрогнозировать уровень рентабельности.
Таблица 1 – Исходные данные
Факторн
ый
показате
ль
Уровень показателя Изменен
ие
факторно
го
показател
я
(Δxi)
Коэффици
ент в
уравнении
регрессии
(а
i
)
Изменен
ие
рентабел
ь-ности,
проц.
пункт
фактиче
ский
планируе
мый
Х1
Х2
Х3
Х4
Х5
1,4
1,2
8
28
27
1,45
1,25
8,6
27,5
30
0,05
0,05
0,6
-0,5
3
3,65
0,09
1,02
-0,122
0,052
0,1825
0,0045
0,612
0,061
0,156
48

Итого 1,016
Фактический уровень рентабельности составлял 11,366%. При
рассчитанном приросте в 1,016 процентных пункта прогнозный
уровень рентабельности составит 12,382% (11,366+1,016).
5.6. Линейное программирование и область его применения в
анализе.
Линейное программирование является одним из разделов
математического программирования, который посвящен теории и
методам решения задач об экстремумах линейных функций на
множествах, задаваемых системами линейных равенств и неравенств.
Задачи линейного программирования являются моделями многих
задач по анализу хозяйственной деятельности. К ним относятся
задачи:
- по определению оптимального ассортимента продукции при
наиболее рациональном использовании трудовых, материальных и
других ресурсов;
- по максимальной загрузке оборудования;
- по получению максимальной прибыли.
Составление математической модели начинают с подбора
показателей и обозначения переменных, совокупность которых
однозначно определяет один из вариантов процесса. Затем строится
целевая функция, которая в математической форме отражает
критерий выбора наилучшего варианта изучаемого экономического
процесса или явления. После этого составляется система ограничений
по имеющимся ресурсам.
Типичным примером задачи линейного программирования может
служить следующая задача, описанная в общем виде: необходимо
определить такой ассортимент выпуска продукции, при котором
прибыль будет максимальной при имеющихся ресурсах.
Введем обозначения. Пусть x
i
– количество продукции i-го вида,
выраженное в натуральном измерении. Тогда целевая функция будет
иметь следующий вид:
n
у = Σ П
i
x
i
max,
i=1
а система ограничений
49
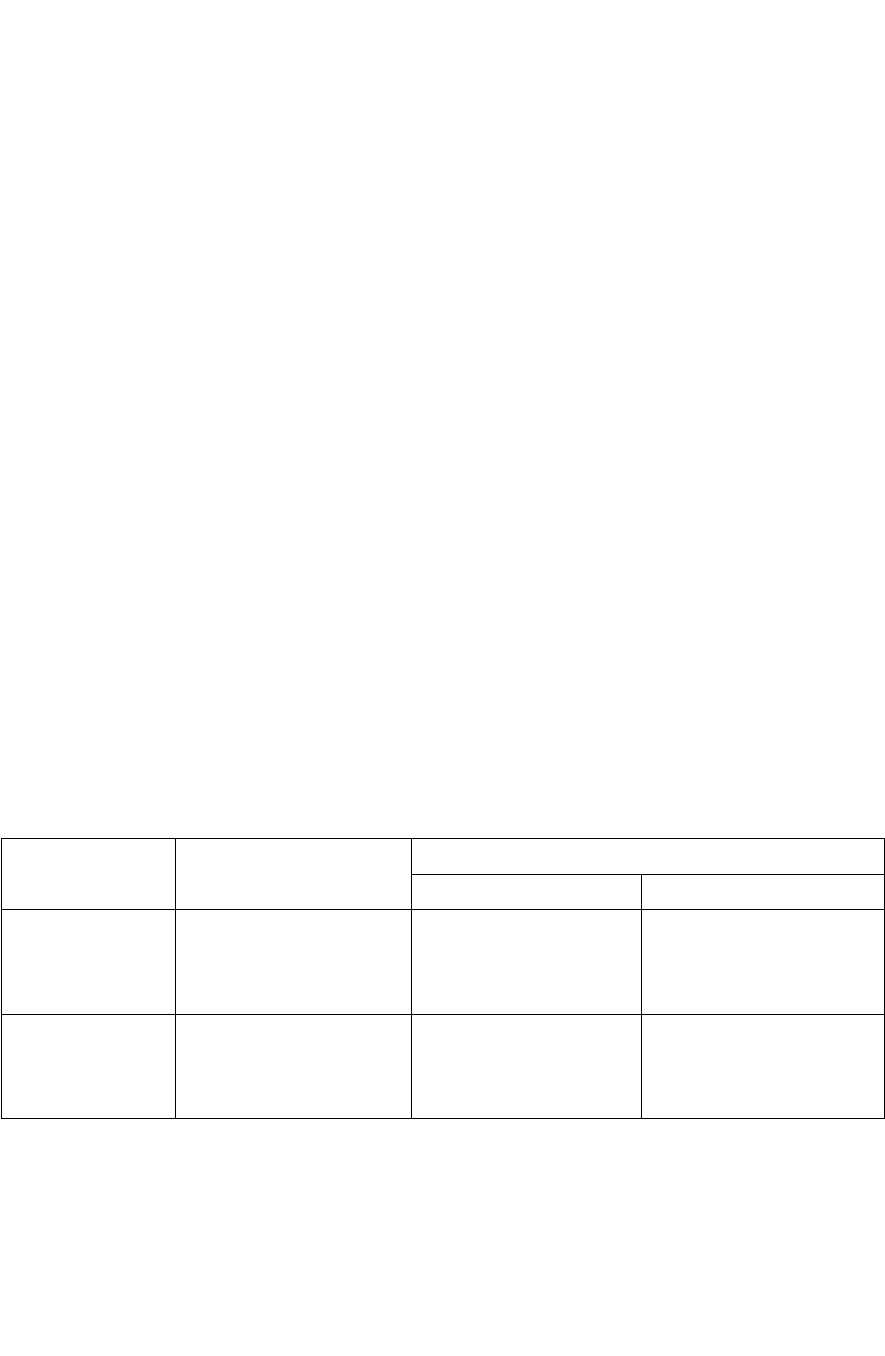
0
i
jiij
x
zxa
,
где Пi - прибыль от реализации единицы продукции i- го вида;
а
ij
- норма расхода j–го вида сырья на единицу i-го вида
продукции;
z
j
- совокупные затраты j-го вида сырья,
j- индекс вида сырья (j = 1:m)
i- индекс вида продукции( I = 1:n).
Наиболее распространенным методом решения задач линейного
программирования является симплексный метод, позволяющий
получить оптимальное решение путем целенаправленного перебора
допустимых вариантов. При каждом расчете определяется новое
допустимое базисное решение, которому соответствует значение
функции, лучшее, чем ее значение в предыдущем расчете. В
результате составления таких последовательных вариантов через
определенное количество «шагов» получают оптимальный вариант,
т.е. такую систему значений переменных, при которых целевая
функция достигает экстремума.
Рассмотрим пример.
Пусть для изготовления 2-х видов продукции используется 3 вида
сырья. Необходимо определить такой ассортимент продукции, при
котором прибыль будет максимальной.
Таблица 2 – Исходные данные
Вид сырья Количество
(запасы) сырья
Норма расхода на 1 изделие
изделие А изделие Б
Первый
Второй
Третий
24
12
30
2
1
3
1
2
0
Прибыль
на единицу,
тыс. руб.
8 3
Обозначим через x
i
количество продукции i-го вида, шт.
Составляем целевую функцию
8x
1
+ 3x
2
мах
Составляем систему ограничений:
0
303
122
242
1
21
21
i
x
x
xx
xx
50
