Месяц Г.А. Импульсная энергетика и электроника
Подождите немного. Документ загружается.


30 Глава
1. Вопросы теории электрических цепей
а соотношение (3) для емкости:
О Л(1.14)
при условии, что емкость разряжена при / < 0.
Законы Кирхгофа и Ома для активных сопротивлений выразим через эти новые
переменные. При этом мы можем использовать обычные правила, иллюстрируе-
мые рис. 1, а также теорему Тевенина, если ввести преобразование Лапласа и при-
менить операторные импедансы рЬ, 1/рС и К. Операторные изображения выходно-
го тока I и входного напряжения V связаны выражением:
Т
=
0(р)П, (1.15)
где 0(р)"~ некоторая функция /?, характеризующая данную цепь. Входное напря-
жение V может быть любой функцией времени, но V является функцией только р,
поэтому I также будет функцией только р.
Таблица 1.1.
Некоторые элементарные изображения Лапласа
Функция времени Изображение Лапласа
ДО,/(0 = 0 при / < 0; /
Л
Р/
<1
п
/ (все низшие производные равны ,
&П нулю при
г
= 0), п = 0,1,2,...
-г
о
р
) }... ]'/(!„)*„...Л
и
« = 0,1,2,...
[1]о
Р"
]_
Р
(
п 1
-, и = 0,1,2,..
и! Р
,п+1
\-е-"
Т
1 + рТ
1
р(1 + рТ)
/((-Т) е-Р
т
/
1е
,-ш
1
(р+а)
2
р
е_<
"
8Ь
Р' р
2
+
2ар+(а
2
-р
2
)

Литература
к
главе
I 31
Остается последняя задача - проведение обратного преобразования, т.е. нахож-
дение оригинала, являющегося функцией времени. Обратное преобразование осу-
ществляется при помощи интеграла Фурье-Меллина в плоскости комплексного
переменного р
где с - положительная постоянная, значение которой выбирается достаточно боль-
шим, так, чтобы все неоднородности функции / лежали слева от границы интег-
рирования.
Литература к главе 1
1.
Льюис
Я.,
Уэлс Ф.
Миллимикросекундная импульсная техника / Пер. с англ. В.Н. Дули-
на под ред. И.С. Абрамсона
и
А.Н. Могилевского. М.: Изд-во иностр. лит., 1956.
2. ИцхокиЯ.С. Импульсные устройства. М.: Сов. радио, 1959.
(1.16)

Глава 2
ДЛИННЫЕ ЛИНИИ
§ 2.1 Введение
Проблема передачи импульсов от одного места к другому без искажений являет-
ся одной из важнейших в импульсной технике. В наносекундном и особенно в пико-
секундном диапазонах длительностей импульсов эта задача становится наиболее
сложной, так как для передачи необходимы широкие полосы частот. Передать им-
пульс даже на расстояние в несколько сантиметров - не просто. Эти трудности обу-
словлены наличием последовательных индуктивностей и параллельно включенных
емкостей между землей и каждым отрезком используемых соединительных провод-
ников. Применение линий передачи позволяет решать эту проблему. Ниже мы пока-
жем, что импульсный сигнал может распространяться вдоль линий без искажений и
что входное сопротивление отрезка линии, нагруженное на волновое сопротивление,
представляет собой чисто активное сопротивление. Эти два важнейших качества
лежат в основе большинства применений линий передачи.
Линии используются для передачи импульсов, их генерирования, трансформа-
ции и других преобразований. Они являются очень важными элементами техники
мощных наносекундных импульсов. В этой главе мы рассмотрим теорию длинных
линий на основе преобразований Лапласа.
Перечислим основные свойства длинных линий [1-3].
1. Линия передачи должна быть образована по крайней мере двумя отдельны-
ми проводниками. Если эти проводники параллельны и их сечение остается неиз-
менным, линия называется однородной. Проблемы многопроводных линий мы
обсуждать не будем.
2. Решения уравнений Максвелла при соответствующих граничных условиях
для простейших полей показывают существование движущейся в прямом и обрат-
ном направлениях электромагнитной волны.
3. Электрическое и магнитное поля в этой волне всегда взаимно перпендику-
лярны и ориентированы под прямым углом к направлению распространения волны.
4. Волновое сопротивление имеет чисто активный характер, и его величина не
зависит от частоты.

§2.1 Введение 33
(а)
(б)
-*— Электрическое поле
Магнитное поле
Рис. 2.1. Распределение поля в поперечном сечении линии: а - для полосковой линии,
состоящей из параллельных пластин; б - для коаксиальной линии. Волна распространяется
в направлении, перпендикулярном плоскости чертежа, от наблюдателя
5. Если линия обладает потерями, то затухание всегда увеличивается с воз-
растанием частоты.
6. Распределение электрического и магнитного полей в некотором поперечном
сечении такое же, как если бы оно было вызвано электростатическим зарядом,
сообщенным проводникам, и текущим по ним током соответственно. Из-за по-
верхностного эффекта токи высокой частоты текут лишь по поверхности провод-
ников, т.е. в слоях более тонких, чем размеры проводников в линии. На рис. 1 по-
казаны соответствующие картины полей для линии, состоящей из двух параллель-
ных пластин (полосковая линия) и для коаксиальной линии.
7. Это распределение полей можно получить, если допустить, что между про-
водниками существует некоторая разность потенциалов и по ним текут токи, рав-
ные по величине, но обратные по знаку. Могут быть введены понятия параллель-
ной емкости Со и последовательной индуктивности Ьо на единицу длины линии,
значения которых можно определить при рассмотрении в статическом режиме или
при помощи квазистационарной теории.
8. Скорость распространения колебаний вдоль линии не зависит от частоты; в
линиях также отсутствует граничное значение низкой частоты, свойственное вол-
новодам. Скорость распространения V равна скорости плоской волны, которая
существовала бы в бесконечно большом объеме диэлектрика, заполняющего про-
странство между проводниками:
где Ь
0
и С
0
- емкость и индуктивность линии на единицу длины линии, которые
называют погонными; с - скорость электромагнитной волны в свободном про-
странстве, 8 и
\х
- относительные диэлектрическая и магнитная постоянные.
9. В любой точке однородной линии отношение напряжения к току является
величиной постоянной, которую называют волновым сопротивлением линии. Обо-
значим его через 2
0
. Иногда его называют характеристическим импедансом линии.
Величина 2
0
= (Ь
0
/С
0
)
112
. Для двух наиболее часто встречающихся типов линий,
полосковой и коаксиальной (рис. 1), волновое сопротивление равно (в Ом):
V
= (А)0))~
1/2
= с(ец)~
1/2
(2.1)
3. Месяц Г.А.

34
Глава 2. Длинные линии
где
Ъ
- ширина полосы, а - расстояние между полосами; В и
(I
- диаметры внеш-
него и внутреннего проводников, 8 - относительная диэлектрическая проницае-
мость диэлектрика.
§ 2.2 Анализ волновых процессов в линии
Волновые процессы в линиях обычно исследуют при помощи теории цепей с
распределенными параметрами. Примем, что 11
х
(г) и
1
Х
(1)
- напряжение и ток в мо-
мент времени ^ в точке х линии (рис. 2). Определяя падение напряжения на не-
большом участке дх благодаря току, текущему в последовательной индуктивности
Ьудх, получим:
Здесь использованы изображения Лапласа для напряжения и тока для данного мо-
мента времени.
Изменение тока в элементе
сЬс,
вызванное напряжением, действующим на ем-
кости
С
0
с1х,
определяется уравнением:
После дифференцирования по х обеих частей уравнения (2) при условии, что Ь
0
не зависит от х, и подстановки сИ
х
Ш из уравнения (3), получим
(2.2)
(2.3)
АЮ -
(2.4)
Аналогично, в предположении, что С
0
не зависит от х, получаем:
И2Т
(2.5)
Легко показать, что если Ь
0
и Со не зависят от х, то
(2.6)
и
(2.7)
х х+с1х
I + Ш1
V
Рис.
2.2.
Анализ линии передачи

§2.2
Анализ волновых процессов в линии
35
есть решения уравнения (4), где С/
0
и [/
0
- постоянные: стрелка вправо означает
волну, бегущую от источника к нагрузке, а стрелка влево - отраженную волну.
Здесь
Т = (2.8)
Общее решение уравнения (4) представляет собой сумму решений (6) и (7):
V
х
=б
х
+П
х
= б
0
е~
рТх
+
а
о
еР
т
*.
(2.9)
Проводя обратное преобразование Лапласа, получаем
Ых (0
=
(0
+
(0
=
(' -
Тх) +
О
0
(* + Тх)
(2.10)
при условии, что
1
-Тх> 0.
Первый член правой части выражения (10) показывает, что напряжение в точ-
ке х в момент времени 1+ Тх такое же, как в точке х = 0 в момент времени /, т.е.
имеет место распространение волны без искажений со временем задержки Т на
единицу длины. Условие
1
-Тх> 0 показывает, что мы не должны учитывать этот
член для точки х до тех пор, пока не истечет время, необходимое для распростра-
нения волны от точки х = 0 до точки х.
Аналогично, второй член относится к волне, распространяющейся с той же
скоростью, но в обратном направлении. Точно такие же соображения лежат в ос-
нове решения уравнения (5) для токов. Вводятся только две новые постоянные 1
Х
и 1
Х
, и вместо выражений (6), (7) и (9) получаем
7
Х
=/
Х
+/
Х
, (2.11)
где
1
х
=?ое-
рТх
(2.12)
(2.13)
Полные решения (9) и (11) должны удовлетворять уравнению (2) или (3) для всех
значений х.
Как мы показали выше, величина волнового сопротивления 2
0
определяется
выражением
о"-
(2Л4)
Поэтому нетрудно показать, что
^
=
^
= = =
(2.15)
/о /о ^х
Ввиду того, что выражение для 2
0
не содержит р, обратное преобразование
Лапласа для выражения (15) заключается лишь в исключении черточек, стоящих
над значениями V и /. Таким образом, мы видим, что волновое сопротивление
определяется отношением напряжения к току в бегущей волне; для отраженной
волны может быть взято отношение этих же величин, но с другим знаком.
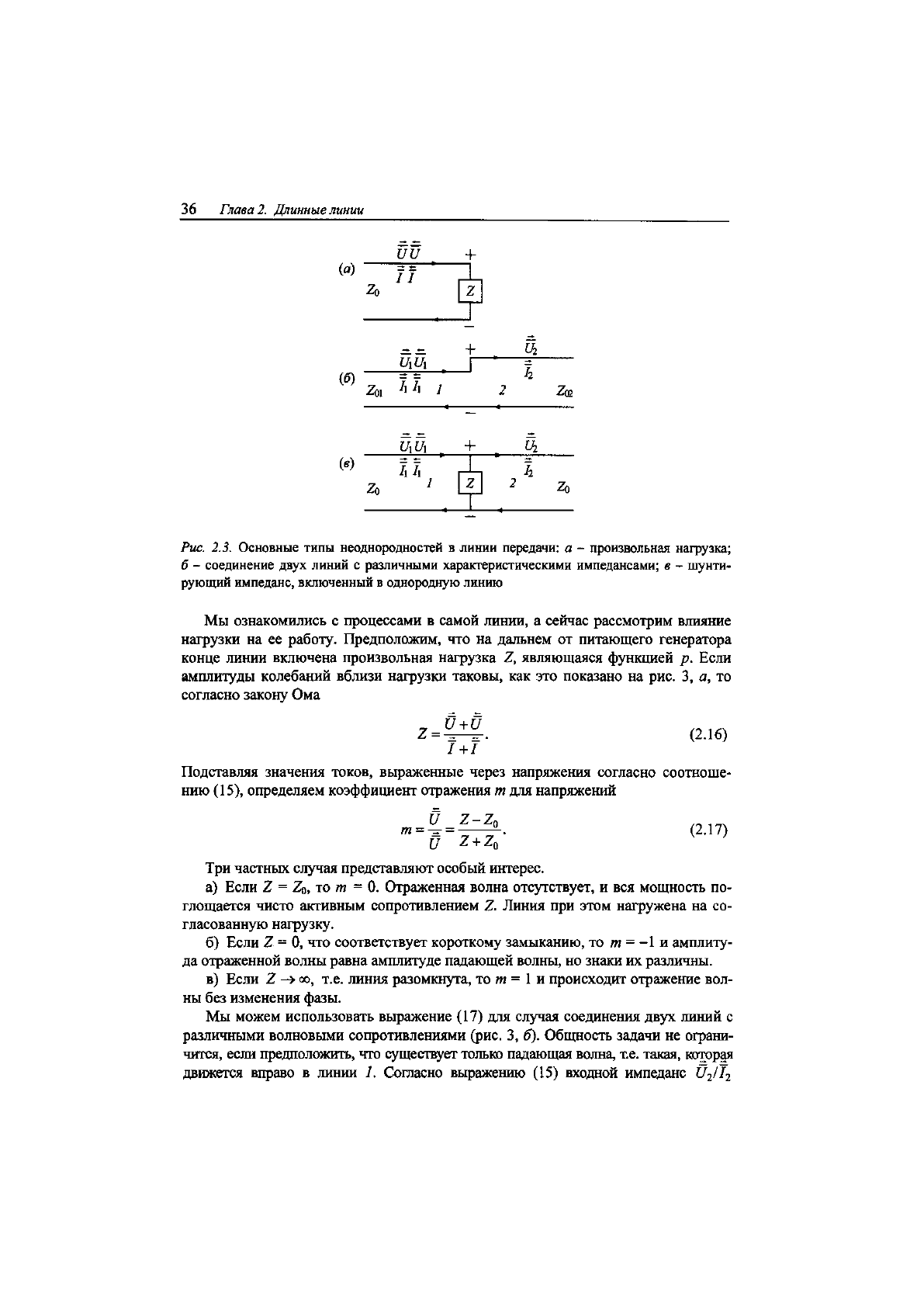
36
Глава 2. Длинные линии
171/
+
2о
11
1
2
+
й\й\
1
%
2
2ш
Их 1
%
2
202
щк ,
+
2
0
%%
1
2
|
1
2
2о
Рис. 2.3. Основные типы неоднородностей в линии передачи: а - произвольная нагрузка;
б - соединение двух линий с различными характеристическими импедансами; в - шунти-
рующий импеданс, включенный в однородную линию
Мы ознакомились с процессами в самой линии, а сейчас рассмотрим влияние
нагрузки на ее работу. Предположим, что на дальнем от питающего генератора
конце линии включена произвольная нагрузка 2, являющаяся функцией р. Если
амплитуды колебаний вблизи нагрузки таковы, как это показано на рис. 3, а, то
согласно закону Ома
2
=
(2.16)
/+/
Подставляя значения токов, выраженные через напряжения согласно соотноше-
нию (15), определяем коэффициент отражения т для напряжений
„М*^. (2.17)
а
Три частных случая представляют особый интерес.
а) Если 2 = 2
0
, то т = 0. Отраженная волна отсутствует, и вся мощность по-
глощается чисто активным сопротивлением 2. Линия при этом нагружена на со-
гласованную нагрузку.
б) Если 2 = 0, что соответствует короткому замыканию, то т = -1 и амплиту-
да отраженной волны равна амплитуде падающей волны, но знаки их различны.
в) Если 2 ->
оо,
т.е. линия разомкнута, то т = 1 и происходит отражение вол-
ны без изменения фазы.
Мы можем использовать выражение (17) для случая соединения двух линий с
различными волновыми сопротивлениями (рис. 3, б). Общность задачи не ограни-
чится, если предположить, что существует только падающая волна, т.е. такая, которая
движется вправо в линии 7. Согласно выражению (15) входной импеданс 1/
2
//
2

§2.3
Неоднородные линии
Ъ1
линии 2 равен 2ог, подстановка этого значения в предыдущее выражение дает
= (2.18)
^02 +
^01
Если в месте соединения не включен какой-либо последовательный сосредоточен-
ный импеданс, то мы имеем
0
1
^6
1
=&
29
(2.19)
и соответственно коэффициент передачи для напряжений определяется как
^- =
1
+ 5- =
1
+
/и.
(2.20)
Если 2о! = 2
02
, то т = 0, и коэффициент передачи равен единице. В месте со-
единения линий с равными импедансами не возникает никаких отражений и про-
исходит полная передача мощности.
Рассмотрим теперь случай включения произвольного импеданса 2 в некоторой
промежуточной точке однородной линии (рис. 3, в). Эффективное значение импеданса
нагрузки для левой части линии равно 22ц/{2 + 2о), и выражение (17) принимает вид
т= . (2.21)
22+ 2
0
В этом случае напряжение в месте неоднородности изменяется непрерывно и вы-
ражения (19) и (20) удовлетворяются.
Аналогичные соображения могут быть применены при определении коэффи-
циентов отражения и передачи для тока в случаях, показанных на рис. 3. В случае
«в» ток не является непрерывной величиной в месте существования неоднородно-
сти, и выражение для токов, аналогичное (19), несправедливо. Выражение (19) для
напряжений также несправедливо, если в линию включен сосредоточенный после-
довательный импеданс. Во всех случаях коэффициенты могут быть найдены при
помощи соотношения (15) для каждой части линии по обе стороны от неоднород-
ности при использовании закона Ома и соответствующих выражений.
Наличие неоднородности в линии и связанных с ней отражений вызывает зату-
хание основной волны. Если неоднородность обусловлена включением чисто актив-
ного импеданса, как это показано на рис. 3, а и в, где 2 является активным сопро-
тивлением, то коэффициент отражения не зависит от р и от частоты; при этом не
возникает никаких искажений. Если неоднородность содержит некоторую реактив-
ность, то т является функцией р и затухание сопровождается искажениями.
§ 2.3 Неоднородные линии
Если погонные индуктивность и емкость плавно меняются по длине линии, то ли-
ния называется неоднородной. При выводе уравнений для тока и напряжения в таких
линиях необходимо иметь в виду, что удельные параметры Ь
0
и Со являются функ-
циями расстояния х. Естественно, что от х будет зависеть волновое сопротивление

38
Глава 2. Длинные линии
В точке х = 0 волновое сопротивление 2
00
= ^Ь
00
/С
00
, где Ь
00
и Соо - индуктив-
ность и емкость в начале линии. Аналогично от х будет зависеть время задержки
на единицу длины
Т
х
=^Ь
0х
С
0х
. (2.23)
Если воспользоваться уравнениями (2) и (3) и учесть, что Ь
0
и С
0
зависят от х
9
а также ввести параметр т(х) - полное время задержки линии от источника до
точки х
т(х)
= ]т{х')(к\ (2.24)
т.е. Ах =
Т(х)сЬс, ТО
получим
1 а
2
й 1 аы2
о
ш_
п = 01 (225)
Р
2
с1т
2
Р
2
с1т с1т
1 1 Л*.
= а (2
.
26)
р
2
с1т
2
р
2
д, т
Эти уравнения используются для анализа процессов в неоднородных линиях.
Они не имеют точного решения в общем виде, а решаются только для некоторых
частных случаев, например для экспоненциальной линии.
В экспоненциальной линии индуктивность и емкость на единицу длины меня-
ются по экспоненте
С
0х
=С
00
е-™
9
(2.27)
где к - положительная или отрицательная постоянная. Волновое сопротивление
тоже меняется по экспоненциальному закону
(2.28)
но время задержки на единицу длины остается неизменным:
Г = = (2.29)
В более общем виде волновое сопротивление экспоненциальной линии равно
2
0
=2
00
е"
/т
о, (2.30)
где т - величина, определяемая выражением (24). Если Т = Го, то т =
Т&с
и выра-
жения (28) и (30) совпадают.
Если подставить (30) в (25) и (26), то получим
1 к
л_
Ош0 (231)
р
2
<1х
2
р
2
Т
0
ах
\ а
2
1 к ^ _ 7 = 0. (2.32)
Р
2
АХ
2
р
2
т
0
АХ
Решением уравнения (31) будет сумма прямой и обратной волн:
(2-33)

§2.3
Неоднородные линии
39
где
Ц
и
= и^г-чут^ (2.34)
0„ =0
Л
е<
к/2+
^
/т
», (2.35)
а постоянные 1}
а
и 1}
а
- амплитуды напряжений волн в начале линии. Величина
9
=
Т>+—. (2.36)
Уравнения для токов (32), содержащие постоянные /
а
и /
а
, будут аналогичны вы-
ражениям (34) и (35) при условии, что знак к меняется на обратный.
Рассмотрим два приближенных решения уравнений (31).
1. На высоких частотах при соГ
0
»|к|/2 в выражении. (36) можно принять
РцТц » к
2
/4. Тогда получим
Я*рТ
0
. (2.37)
В этом случае для экспоненциальной бесконечно длинной линии с возрастаю-
щим от начала к концу волновым сопротивлением в точке т =
Т&с
произойдет уве-
личение амплитуды волны напряжения в п раз, где
„ = в"/2Гв = /—. (2.38)
V
200
2. В качестве второго приближения используем два первых члена разложе-
ния # в ряд, т.е.
Я
= (2.39)
8 рТ
0
Тогда для волны, двигающейся в бесконечно длинной линии из начала (х = 0),
получим
Выражение в скобках показывает, что если мы имеем прямоугольный импульс
с единичной амплитудой, то его вершина будет после прохождения пути за вре-
мя т спадать по линейному закону, определяемому выражением [1]
где - длительность импульса (рис. 4).
В [1] рекомендуется приближенная формула, связывающая величины к, А и
при пробеге волной линии длиной /:
(2
.4
2)
1Т
0
Из этой формулы, в частности, следует, что если допустимое снижение им-
пульса
А
= 0,1, то амплитуда импульса увеличится в 1,5 раза при времени задерж-
ки, равном длительности импульса.
