Месяц Г.А. Импульсная энергетика и электроника

Подождите немного. Документ загружается.

Список сокращений

А анод

АФ анодный факел

АФАР активная фазированная антенная решетка

АЧХ амплитудно-частотная характеристика

АЭЭ автоэлектронная эмиссия

ВАХ вольтамперная характеристика

ВК виртуальный катод

ВКЛ вакуумная коаксиальная линия

ВЭК взрывоэмиссионный катод

ВЭЭ взрывная эмиссия электронов

ГМ генератор Маркса

Д ДРВ дрейфовый диод с резким восстановлением

ДН диаграмма направленности

ДНЗ диод с накоплением заряда

ДС двойной слой

ДФЛ двойная формирующая линия

ЕНЭ емкостный накопитель энергии

ЗС замедляющая система

ИВТ импульсный водородный тиратрон

ИК инфракрасный

ИТ инжекционный тиратрон

К катод

КДМИ коаксиальный диод с магнитной изоляцией

кпд коэффициент полезного действия

КСВН коэффициент стоячей волны по напряжению

КФ катодный факел

ЛБВ лампа бегущей волны

ЛИТ линейный импульсный трансформатор

ЛИУ линейный индукционный ускоритель

ЛОВ лампа обратной волны

ЛСП лазер на самоограниченных переходах

Список сокращений

МВЧГ многоволновой черенковский генератор

МГД магнитогидродинамический

МДК металлодиэлектрический катод

МИГ-лазер мощный импульсный газовый лазер

МИД магнито-изолированный диод

МИП мощный ионный пучок

мк магнитный компрессор

мппт

микросекундный плазменный прерыватель тока

МЦАР мазер на циклотронном авторезонансе

МЦР

мазер на циклотронном резонансе

003

область объемного заряда

опв

область первоначального включения

осп область сильного поля

ПБС

пучок большого сечения

гшт

плазменный прерыватель тока

ПТ

пауза тока

РВД

реверсивно включаемый динистор

РГПВ

релятивистский генератор поверхностной волны

РЛС

радиолокационная станция

РПЭ

распределение поглощенной энергии

РЭП

релятивистский электронный пучок

СВЧ

сверхвысокие частоты

сдц

селекция движущихся целей

СИ

сверхизлучение

СШП

сверхширокополосный

ТЗУ

тиристорное зарядное устройство

тт

тройная точка (металл-диэлектрик-вакуум)

тэ

термализованные электроны

УВП

узел взрыва проводников

УФ

ультрафиолетовый

УЭВ

ударная электромагнитная волна

ФЛ

формирующая линия

ФЭУ

фотоэлектронный умножитель

ЭВМ

электрический взрыв металла

ЭВП

электрический взрыв проводников

эдс

электродвижущая сила

ЭОП

электронно-оптический преобразователь

ЭРЖ

электрический разряд в жидкости

808

зегмсопёис^ог орепт§

З\УЙСЬ

- полупроводниковый

размыкающий коммутатор

Список сокращений

Названия организаций

ВНИИТФ ВНИИ технической физики

ВНИИЭФ ВНИИ экспериментальной физики

ИАЭ Институт атомной энергии им. И.В. Курчатова

ИОФАН Институт общей физики им. А.М. Прохорова РАН

ИПФ Институт прикладной физики РАН

ИСЭ Институт сильноточной электроники СО РАН

ИЭФ Институт электрофизики УрО РАН

ИЯФ Институт ядерной физики им. Г.И. Будкера СО РАН

НИИЭФА НИИ электрофизической аппаратуры им. Д.В. Ефремова

СФТИ Сухумский физико-технический институт

ТПУ Томский политехнический университет

ФИАН Физический институт им. П.Н. Лебедева РАН

ФТИ Физико-технический институт им. А.Ф. Иоффе РАН

ЬА1МЪ Ьо§ А1ато$ Кайопа! ЬаЬога1огу

ЖЬ Кайопа1 КезеагсЬ ЬаЪога1огу

8№. 8ап<На

Ыайопа1

ЬаЬога1опез

ТГО Техаз ТесЬпо1о§1са1 Ш1УегзИу

Часть I ОСНОВЫ ИМПУЛЬСНОЙ ТЕХНИКИ

Глава 1

ВОПРОСЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

§ 1.1 Основные законы электрических цепей

В этой главе мы кратко познакомим читателя с простейшей теорией цепей, с

терминологией, которая в ней используется, а также методами расчета переходных

процессов. Теория цепей является основой импульсной техники [1,2]. Вначале для

простоты рассмотрим простейшие цепи, включающие линейные сопротивления К,

подчиняющиеся закону Ома

1/ = Ж, (1.1)

где I - ток, II - падение напряжения на сопротивлении К. В линейном случае это

сопротивление не зависит от протекающего через него тока и приложенного на-

пряжения. Однако техника мощных наносекундных импульсов в значительной

мере основана на применении нелинейных элементов, анализ которых будет дан

нами в других разделах книги.

Основными законами, на которых основана теория цепей, являются два закона

Кирхгофа. Один из них гласит: в любом замкнутом контуре сумма падений на-

пряжений на сопротивлениях равна сумме электродвижущих сил (эдс). Другой - в

любом электрическом узле сумма токов равна нулю. Если в цепи содержится не-

сколько узлов и контуров, то электрические процессы в ней описываются системой

уравнений, полученных из упомянутых выше двух законов Кирхгофа. Они назы-

ваются уравнениями цепи. Эти уравнения линейны по отношению к изменениям

напряжения и тока, если элементы цепи линейны. В этом случае к цепям приме-

ним принцип суперпозиции: если в одной точке цепи (на входе) приложена эдс

вызывающая в другой точке (на выходе) ток

а вторая эдс &2 на выходе вызыва-

ет ток /

, то эдс +&2 будет вызывать ток

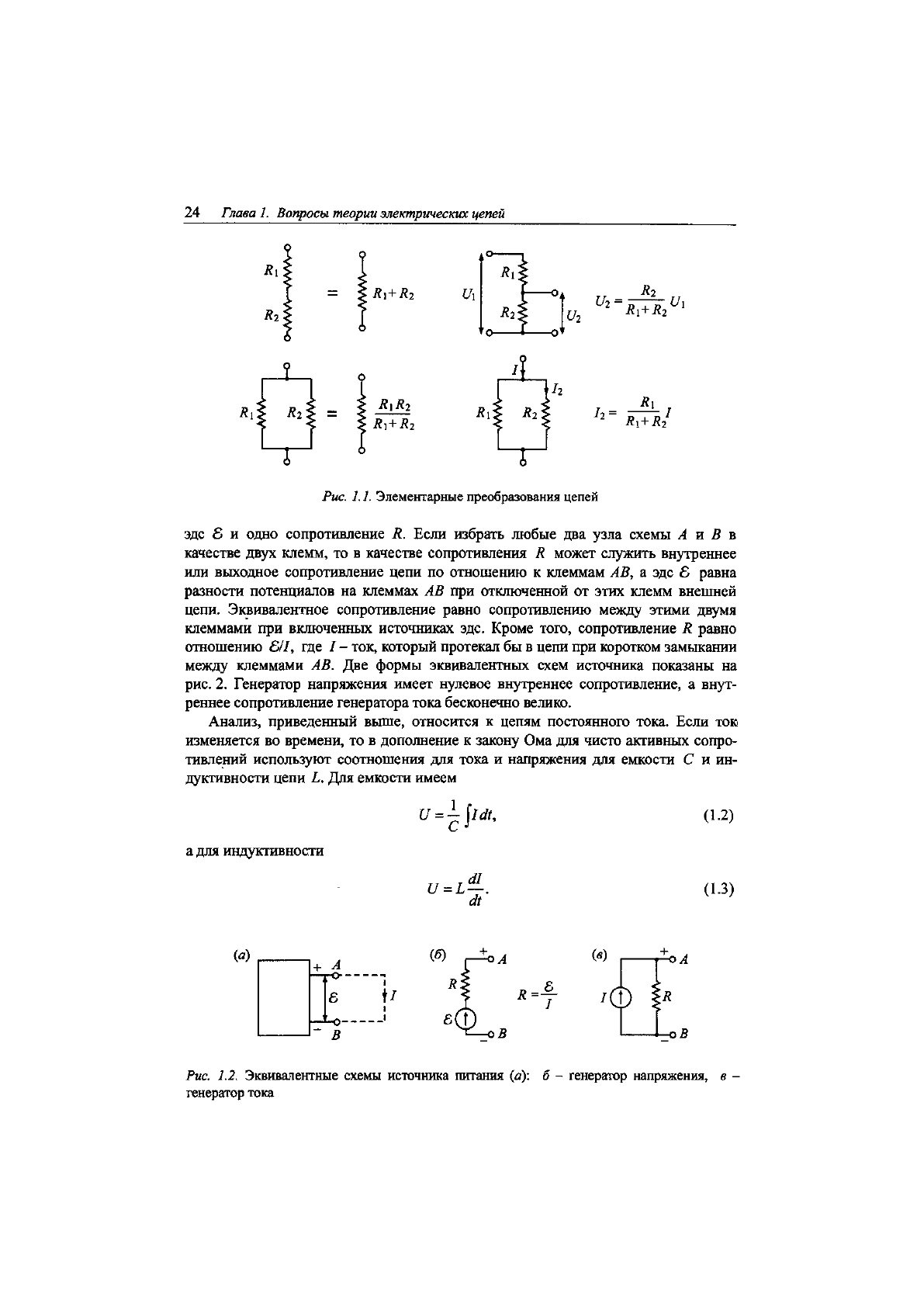
Решение уравнений цепи часто может быть упрощено, если применить ряд

правил, которые приведены на рис. 1, а также если использовать теорему Тевени-

на. Согласно этой теореме, любые нагруженные цепи, составленные из линейных

сопротивлений и источников эдс, эквивалентны цепи, содержащей один источник

24 Глава

1. Вопросы теории электрических цепей

Кх

К1+К2

ЯгК

Я1+К2

+К

Рис.

1.1.

Элементарные преобразования цепей

эдс 6 и одно сопротивление К. Если избрать любые два узла схемы А и В в

качестве двух клемм, то в качестве сопротивления К может служить внутреннее

или выходное сопротивление цепи по отношению к клеммам АВ, а эдс Б равна

разности потенциалов на клеммах АВ при отключенной от этих клемм внешней

цепи. Эквивалентное сопротивление равно сопротивлению между этими двумя

клеммами при включенных источниках эдс. Кроме того, сопротивление К равно

отношению 6//, где I - ток, который протекал бы в цепи при коротком замыкании

между клеммами АВ. Две формы эквивалентных схем источника показаны на

рис. 2. Генератор напряжения имеет нулевое внутреннее сопротивление, а внут-

реннее сопротивление генератора тока бесконечно велико.

Анализ, приведенный выше, относится к цепям постоянного тока. Если ток

изменяется во времени, то в дополнение к закону Ома для чисто активных сопро-

тивлений используют соотношения для тока и напряжения для емкости С и ин-

дуктивности цепи Ь. Для емкости имеем

а для индуктивности

(1.2)

(1.3)

(в)

+ _А

-о А

-о В

Рис. 1.2. Эквивалентные схемы источника питания (а): б - генератор напряжения, в -

генератор тока

§1.2

Анализ Фурье

Соотношение (2) является выражением для тока смещения, а (3) - для эдс само-

индукции. В уравнении Кирхгофа эдс самоиндукции 8 = -Ь(сИ/Л) ставят в той

части уравнения, где находится сумма эдс. Если же ее перенести в ту часть, где

находится сумма падений напряжений, то знак минус сменится на знак плюс, и

величину

Ь(сШс11)

можно формально рассматривать как падение напряжения на

индуктивности.

Примем, что емкости и индуктивности не зависят от напряжения и тока. Будем

также считать, что параметры К

Ь, С не зависят от времени. В этом случае урав-

нения цепи будут представлены семейством обычных линейных дифференциаль-

ных уравнений с постоянными коэффициентами. Метод расчета цепей с исполь-

зованием этих уравнений называют классическим.

Эти уравнения решаются наиболее просто, если приложенные эдс изменяются

по синусоидальному закону. В этом случае дифференциальные уравнения могут

быть заменены алгебраическими для различных амплитуд и фазовых углов. Теория

функций комплексного переменного позволяет получать алгебраические уравнения

непосредственно на основании анализа цепи без составления дифференциальных

уравнений. Например, напряжение V, которое изменяется синусоидально с угловой

частотой со, имеет амплитуду II

и фазу ф, может быть записано в виде действи-

тельной части комплексной величины

С/

е/(®'+Ф) (1.4)

где V = - комплексная амплитуда. При подстановке комплексных величин

(4) в (2) и (3) временной множитель пропадает и комплексные амплитуды напря-

жения и тока определяются соотношениями, аналогичными закону Ома. Величины

усоЬ и 1//соС называют реактивными сопротивлениями в отличие от активного

сопротивления К. Реактивные сопротивления усоЬ и 1/у'соС будут в расчетах учи-

тываться, как и сопротивление К.

Законы Кирхгофа могут быть распространены на эти комплексные величины, и

могут быть использованы правила, аналогичные показанным на рис. 1, при под-

становке в эти соотношения наряду с разностью потенциалов и токами комплекс-

ных реактивных сопротивлений у©! и 1/усоС, а также К и комплексных ампли-

туд эдс. В общем виде суммарное сопротивление всех трех компонентов называют

импедансом и обозначают буквой 2. Отметим, что правила сложения импедансов

такие же, как и для сопротивления К.

Справедливой будет также теорема Тевенина при условии, что эдс различных

частот должны быть представлены отдельными эквивалентными схемами для каж-

дой частоты. Суммарные ток и напряжение будут определяться путем сложения.

§ 1.2 Анализ Фурье

В этом разделе мы рассмотрим расчет схемы при подаче на ее вход импульса.

Теорема Фурье устанавливает, что любая функция времени эквивалентна сумме

непрерывных синусоидальных колебаний с частотами от нуля до бесконечности с

соответствующими (для каждой частоты) амплитудами и фазами. Если функция

периодическая, то частотный спектр состоит из дискретных компонент, частоты

которых находятся в гармоническом соотношении, а амплитуды конечны. Для

26 Глава

1. Вопросы теории электрических цепей

одиночного импульса спектр становится сплошным; амплитуда каждой компоненты

стремится к нулю и заменяется плотностью амплитуды на единицу частоты, а сумма

заменяется интегралом.

Если /(/) - функция времени, представляющая собой импульс, то выражение

для относительной комплексной амплитуды А(со) при угловых частотах, лежащих

между со и

со

Асо,

имеет следующий вид:

ни»

А(А>)

= $ (1.5)

-00

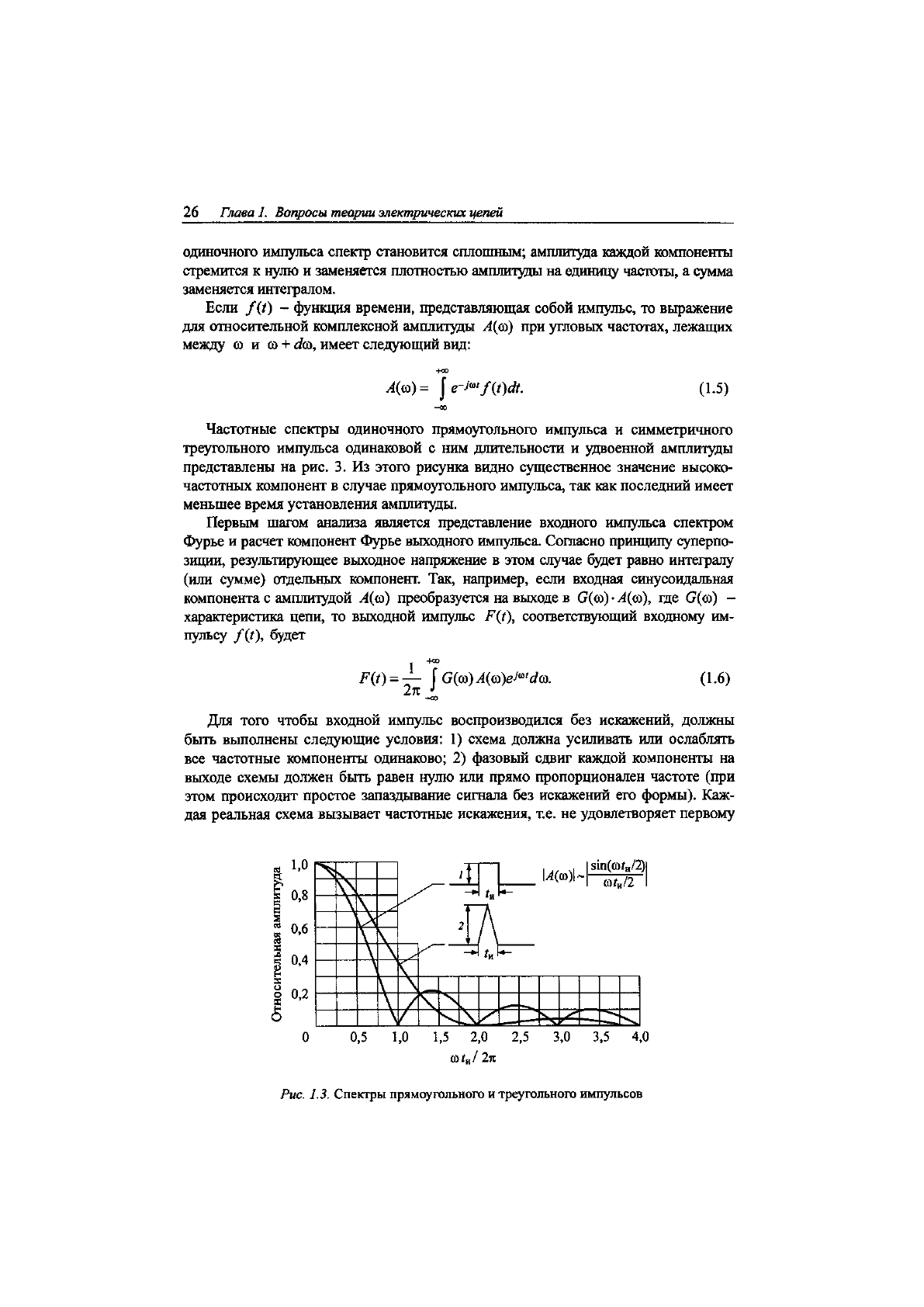
Частотные спектры одиночного прямоугольного импульса и симметричного

треугольного импульса одинаковой с ним длительности и удвоенной амплитуды

представлены на рис. 3. Из этого рисунка видно существенное значение высоко-

частотных компонент в случае прямоугольного импульса, так как последний имеет

меньшее время установления амплитуды.

Первым шагом анализа является представление входного импульса спектром

Фурье и расчет компонент Фурье выходного импульса. Согласно принципу суперпо-

зиции, результирующее выходное напряжение в этом случае будет равно интегралу

(или сумме) отдельных компонент. Так, например, если входная синусоидальная

компонента с амплитудой А(со) преобразуется на выходе в 0(со)

•

Дсо), где О(со) -

характеристика цепи, то выходной импульс соответствующий входному им-

пульсу /(0, будет

= — [

О(со) А(со)е/°><</со.

(1.6)

2 п *

-00

Для того чтобы входной импульс воспроизводился без искажений, должны

быть выполнены следующие условия: 1) схема должна усиливать или ослаблять

все частотные компоненты одинаково; 2) фазовый сдвиг каждой компоненты на

выходе схемы должен быть равен нулю или прямо пропорционален частоте (при

этом происходит простое запаздывание сигнала без искажений его формы). Каж-

дая реальная схема вызывает частотные искажения, т.е. не удовлетворяет первому

1,0

0,8

1 0,2

О 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0

Рис.

1.3.

Спектры прямоугольного

треугольного импульсов

§1.2

Анализ Фурье

условию, и, кроме того, вызывает фазовые искажения, не удовлетворяющие второ-

му условию.

Конкретная схема имеет определенную полосу пропускаемых частот, в преде-

лах которой форма сигнала мало зависит от частоты, а вне этой полосы сигнал

спадает до нуля, а также определенный участок фазовой характеристики, в преде-

лах которого изменение фазы прямо пропорционально частоте. Легко видеть, что

время нарастания переднего фронта выходного импульса при входном импульсе

прямоугольной формы не может быть много меньше одной четверти периода верх-

ней граничной частоты, определяемой частотной характеристикой системы, а об-

щая длительность выходного импульса не может быть много больше полупериода

низшей граничной частоты. В импульсных схемах особое значение имеет менее

привычное понятие фазовой полосы пропускания. С точки зрения получения ми-

нимальных искажений более предпочтительным является отсутствие на выходе

некоторых частотных компонент, чем их воспроизведение с неправильными фазо-

выми соотношениями. В последнем случае высокочастотные компоненты не обес-

печивают быстрого нарастания импульса, а вызывают нежелательные выбросы,

накладывающиеся на передний фронт выходного импульса. Эти выбросы могут

возникать непосредственно перед началом нарастания импульса и в конце перед-

него фронта, а также искажать вершину импульса. Такое явление легко обнаружи-

вается, но весьма трудно устраняется. Поскольку фазовая и частотная характери-

стики тесно связаны, не всегда просто обеспечить резкий спад амплитудной харак-

теристики для тех частот, при которых фазовая характеристика отклоняется от

прямой линии.

Имеется много теоретических исследований, посвященных соотношениям ме-

жду шириной полосы пропускания и длительностью импульса и включающих рас-

смотрение наилучшего метода определения времени нарастания. Простым практи-

ческим методом является определение интервала времени между точками, соответ-

ствующими 10% и 90% конечной амплитуды. При этом длительность фронта

импульса /ф приближенно определяется следующим соотношением [1]:

где /

- верхняя граничная частота частотной характеристики.

Если несколько схем соединены последовательно, то их амплитудно-частотные

характеристики перемножаются (или складываются в децибелах), а фазово-час-

тотные характеристики складываются. Обычно приходится сталкиваться с увели-

, чением времени нарастания импульса при его прохождении через всю электри-

ческую цепь. При этом применяется следующее приближенное правило. Если

через /ф обозначить время нарастания в отдельных частях цепи для случая, когда

на каждую из них поступает прямоугольный импульс, то полное время нараста-

ния т

во всей системе будет равно:

Нижняя граничная частота спектра /

системы определяется максимальной

длительностью пропускаемого импульса.

(1.8)

28 Глава

1. Вопросы теории электрических цепей

Итак, импульсные сигналы характеризуются спектром частот, который, строго

говоря, имеет бесконечную ширину. Однако интенсивность спектра убывает с рос-

том частоты. Как показывает практика, допустимо пренебречь действием тех гармо-

нических составляющих импульса, которые характеризуются малой величиной мо-

дуля спектральной характеристики. Вводится понятие об активной ширине спектра,

заключающей в себе лишь те важнейшие гармонические составляющие сигнала,

эффект воздействия которых является преобладающим и практически определяю-

щим воздействие сигнала на устройство.

Само понятие активной ширины спектра трактуется по-разному. Чаще всего

под ней понимают тот наименьший диапазон частот, в котором сосредоточена оп-

ределенная доля полной энергии сигнала [2] или важнейшие гармонические со-

ставляющие импульса. Чаще всего за эту долю принимают 95% от энергии сигнала

и вводят из этих соображений понятие ширины спектра частот А/. Для типичных

форм импульсов [2] самая широкая полоса частот соответствует прямоугольному

импульсу (А/

2//

), а самая узкая - треугольному (А/

1/2/

). Иногда пользу-

ются средней полосой частот

А/*

= (/

+ /

)/2. Подробнее об этом мы еще будем

говорить в главе 32.

§ 1.3 Метод интеграла Дюамеля

При теоретическом и экспериментальном анализе импульсных сигналов более

удобна ступенчатая функция, чем синусоидальные колебания. Единичная ступенча-

тая функция, обозначаемая [1]

, равна нулю для всех значений времени вплоть до

/ = 0 и равна единице после этого момента времени. Любое колебание может быть

представлено в виде суммы некоторого числа единичных функций, соответствую-

щих амплитуд и знаков, смещенных на необходимые интервалы. Например, прямо-

угольный импульс высотой А и длительностью начинающийся в момент г = О,

можно записать в виде Д[1]

-[1]/

), где индексы обозначают моменты возникно-

вения ступенчатых функций. Согласно принципу суперпозиции, результирующее

выходное напряжение будет равно сумме напряжений, обусловленных единичными

функциями, из которых состоит входное колебание. Если 1%($) - выходная реакция

на единичную входную функцию при I - 0, то импульс на выходе в момент вре-

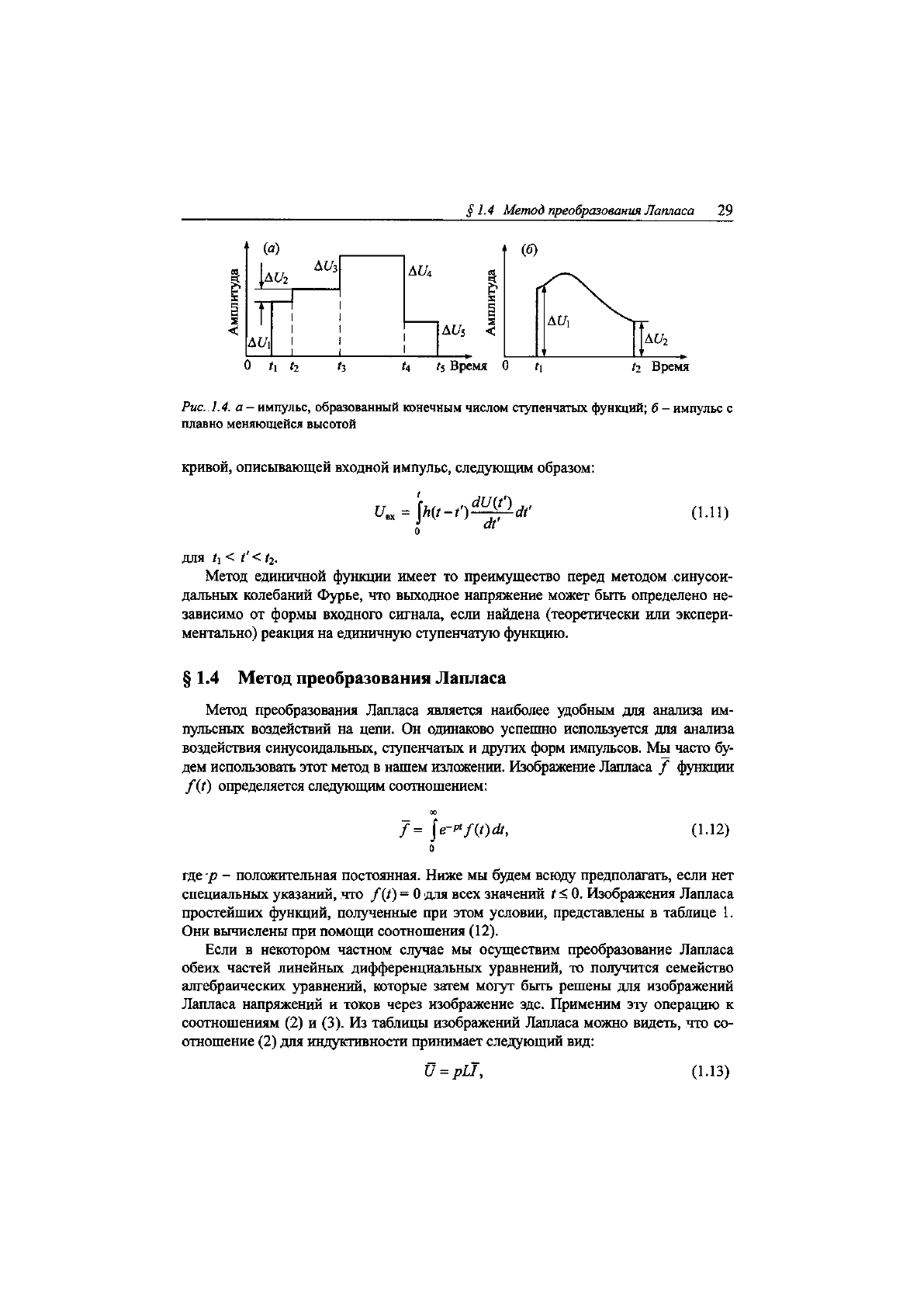
мени и соответствующий входному сигналу, изображенному на рис. 4, а, можно

представить в виде

где суммирование проводится по всем кусочно-гладким участкам. Если часть

входного импульса (или весь импульс) описывается гладкой кривой, то амплитуды

ступенек и интервалы между ними стремятся к нулю. Сумма преобразуется при

этом в интеграл Дюамеля, вычисляемый вдоль гладкой кривой, и выходное напря-

жение в момент времени ( определяется выражением

(1.9)

г/вых = +

(1.10)

для < < Для общности мы сохранили два разрыва кривой, как показано, на-

пример, на рис. 4, б. Кроме того, интеграл может быть выражен через производную

§1.4

Метод преобразования Лапласа

Рис.

1.4.

а- импульс, образованный конечным числом ступенчатых функций; б - импульс с

плавно меняющейся высотой

кривой, описывающей входной импульс, следующим образом:

= (1.11)

для и< {<г

Метод единичной функции имеет то преимущество перед методом синусои-

дальных колебаний Фурье, что выходное напряжение может быть определено не-

зависимо от формы входного сигнала, если найдена (теоретически или экспери-

ментально) реакция на единичную ступенчатую функцию.

§ 1.4 Метод преобразования Лапласа

Метод преобразования Лапласа является наиболее удобным для анализа им-

пульсных воздействий на цепи. Он одинаково успешно используется для анализа

воздействия синусоидальных, ступенчатых и других форм импульсов. Мы часто бу-

дем использовать этот метод в нашем изложении. Изображение Лапласа / функции

/(/) определяется следующим соотношением:

7= (1-12)

где р - положительная постоянная. Ниже мы будем всюду предполагать, если нет

специальных указаний, что /(/) = 0 для всех значений / < 0. Изображения Лапласа

простейших функций, полученные при этом условии, представлены в таблице 1.

Они вычислены при помощи соотношения (12).

Если в некотором частном случае мы осуществим преобразование Лапласа

обеих частей линейных дифференциальных уравнений, то получится семейство

алгебраических уравнений, которые затем могут быть решены для изображений

Лапласа напряжений и токов через изображение эдс. Применим эту операцию к

соотношениям (2) и (3). Из таблицы изображений Лапласа можно видеть, что со-

отношение (2) для индуктивности принимает следующий вид:

(1.13)