Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

432 10 Quasicrystals

restricted to relatively high temperatures. The low-temperature experiments

performed under conﬁning hydrostatic pressure [702, 710] did not allow the

measurement of detailed deformation data.

10.4.1 i-Al–Pd–Mn

Abundant deformation data are available on icosahedral quasicrystals includ-

ing Al–Cu–Fe and Zn–Mg–Dy (e.g., [725,726]) as well as on Al–Pd–Mn (e.g.,

[727–730]). The ﬁrst intrinsic deformation data on icosahedral single qua-

sicrystals were those in [727]. At present, the most comprehensive set of

data of an icosahedral single quasicrystal is certainly that of i-Al-Pd-Mn

in [16, 337, 709, 731]. The following description is based on these data. Of

the low-temperature experiments performed under conﬁning hydrostatic pres-

sure [702, 710,732], only the measurements on icosahedral Mg–Zn–Y in [732]

yielded ﬂow stress data. Accordingly, the yield stress is possibly independent

of temperature near room temperature but decreases rapidly above about

100

◦

At ambient pressure and a standard strain rate of ˙ε

=10

−5

−1

,thereisa

brittle-to-ductile transition (BDT), that means most specimens break below

about 630

◦

C. The BDT temperatures for two other strain rates are indicated

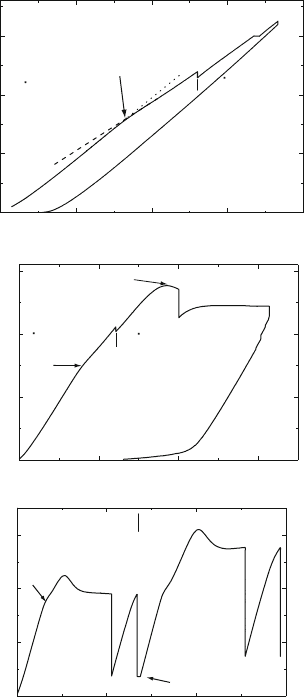
in Fig. 5.29. Typical stress–strain curves of icosahedral Al-21at%Pd-8.5at%Mn

are shown in Fig. 10.32. Figure 10.32a presents an example of 487

◦

C, which is

almost the lowest temperature achieved without fracture. Since the specimens

are very brittle at these low temperatures, low total strain rates were applied,

mostly 10

−6

−1

. There appears a knee in the deformation curve, which marks

a transition from almost elastic to elastic-plastic deformation with a very high

rate of work-hardening. This transition is called the elastic limit and labeled

EL in Fig. 10.32. It corresponds to an instantaneous increase in the plastic

strain rate. As shown in Fig. 10.32a, the elastic limit is determined as the

intersection between tangents to the stress–strain curve before the transition

point (dotted line) and after it (dashed line). Below 550

◦

C, the experiments

were stopped at stresses around 1.5 GPa to prevent fracture. For measuring

the strain rate sensitivity of the ﬂow stress, stress relaxation tests R

were

carried out by keeping the total strain ˙ε

constant. These tests increase the

plastic strain at low strain rates. Additional plastic deformation can also be

achieved under creep conditions at constant load (L).

Figure 10.32b shows the stress–strain curve for deformation at 580

◦

With increasing strain, the curve bends down, passes a maximum, i.e., the

upper yield point (UYP), and ends up in a range of almost steady state

deformation. During steady state deformation, the work-hardening is balanced

by recovery. The temperature in Fig. 10.32b is the lowest one with the upper

yield point being overcome before sample failure. The stress at the elastic limit

is much lower than the steady state ﬂow stress. During the stress relaxation R

performed after the upper yield point, the stress relaxes more strongly than

during the relaxation R

in the initial work-hardening range. Both relaxations

10.4 Macroscopic Deformation Parameters 433

0.0

500

1000

1500

0.5 1.0 1.5 2.0

(%)

=3*10

-6

-1

=10

-6

-1

σ (MPa)

(a)

500

1000

1500

123

(%)

=5*10

−6

−1

=10

−6

−1

σ (MPa)

UYP

(b)

200

400

600

123

(%)

σ (MPa)

(c)

UYP

T = 751 °C T = 719 °C

Fig. 10.32. Stress–strain curves of i-Al–Pd–Mn at diﬀerent temperatures including

stress relaxation curves R

.(a) T = 487

◦

C, ˙ε

=3×10

−6

−1

and change to 10

−6

−1

as well as some deformation under constant load (L). (b) T = 580

◦

C, ˙ε

=5×

−6

−1

and change to 10

−6

−1

.(c) T = 751

◦

C and change to T = 719

◦

C, ˙ε

−4

−1

. Data from [337]

were stopped at about ln[˙σ(MPa s

−1

)] = −3, corresponding to a plastic strain

rate of about 5 ×10

−7

−1

Turning to higher temperatures, the steady state ﬂow stress decreases

drastically, so that it becomes only slightly higher than the elastic limit, as

demonstrated in Fig. 10.32c for 751

◦

C at a strain rate of ˙ε

=10

−4

−1

.In

this experiment, a temperature change experiment TC was performed down

to the lower temperature of 719

◦

C. This is connected with an increase in the

434 10 Quasicrystals

ﬂow stress. During the second deformation into the steady state, a yield drop

eﬀect again occurs. Apart from these changes of the deformation conditions,

the ﬂow stress reaches a steady state value after passing the yield drop, which

is characteristic of the deformation at high temperatures. Such deformation

curves are described in most papers on quasicrystal deformation. At large

strains, the true ﬂow stress may decrease (e.g., [728–730]). In many papers, this

softening is considered a characteristic feature of quasicrystal deformation.

Not all experiments exhibit a distinct initial range of high work-hardening. It

is pronounced in specimens with a twofold compression axis.

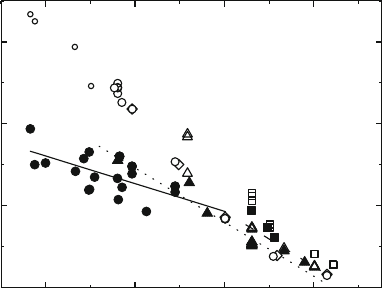
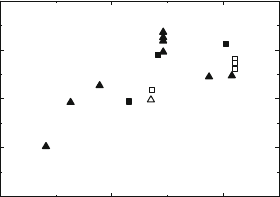
Figure 10.33 summarizes the temperature dependence of the elastic limit

and of the steady state ﬂow stress. The latter is chosen since the interpretation

is more simple for data measured during steady state. The ﬂow stresses are

quite isotropic, i.e., there is practically no diﬀerence between deformation

along the twofold and ﬁvefold compression axes. Both the elastic limit and the

steady state ﬂow stress decrease with increasing temperature. As mentioned

above, the steady state ﬂow stress is only slightly higher than the stress at the

elastic limit for temperatures above about 650

◦

C and a strain rate of 10

−5

−1

For lower temperatures, however, the diﬀerence between both increases with

decreasing temperature. At a total strain rate of 10

−6

−1

, the elastic limit

becomes equal to the steady state ﬂow stress at 700

◦

C and is not observed

above this temperature. The small open symbols below 570

◦

C, where steady

500

1000

1500

700 800600

T (°C)

σ (MPa)

Fig. 10.33. Temperature dependence of the steady state ﬂow stress (open symbols)

and the elastic limit (full symbols). The four small open symbols at low temperatures

correspond to the maximum stresses reached in the experiments where steady state

ﬂow was not achieved. The total strain rates ˙ε

are 10

−6

−1

(circles), 2 × 10

−6

−1

(diamonds), 10

−5

−1

(triangles), and 10

−4

−1

(squares). The straight lines represent

linear regression curves through the elastic limits measured at 10

−6

−1

(full line)and

−5

−1

(dotted line) as well as the steady state ﬂow stresses at higher temperatures

at 10

−5

−1

(dashed line). Data from [337]

10.4 Macroscopic Deformation Parameters 435

state deformation was not achieved because of the brittleness of the specimens,

correspond to the maximum stresses reached in these deformation tests still

before the upper yield point.

In the initial range of high work-hardening, the work-hardening coeﬃcient

θ =dσ/dε is in the range of the elastic stiﬀness modulus S of the specimen and

the parts of the deformation machine inside the strain measurement circuit. θ

increases with decreasing temperature. As described in Sect. 2.1, S is measured

from the slope of the unloading curves at the end of the experiments. The

stiﬀness values increase with decreasing temperature between about 80 and

120 GPa. Using these values results in θ ≈ S at high temperatures, and θ ≈

3S at low ones. These are very high values of work-hardening. They will be

interpreted in Sect. 10.5.8.

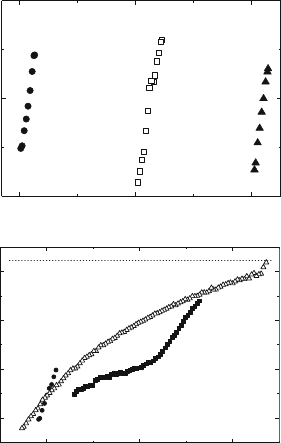
As indicated in Fig. 10.32, stress relaxation tests were performed dur-

ing all experiments to study the strain rate sensitivity r of the ﬂow stress.

Figure 10.34a presents three relaxation curves measured above the elastic

limit within the work-hardening range at the low temperature of 547

◦

C. These

σ (MPa)

In[–dσ/dt (MPa s

−1

)]

800 1000 1200

−3

−4

−5

(a)

σ (MPa)

In[–dσ/dt (MPa s

–1

)]

100 200 300

–2

–4

(b)

Fig. 10.34. Stress relaxation curves of i-Al–Pd–Mn taken in diﬀerent stages of

deformation and at diﬀerent temperatures. (a) T = 547

◦

C. Relaxations taken above

the elastic limit at diﬀerent plastic strains. The total strain rate ˙ε

before the relax-

ations corresponds to ln(− ˙σ)=−2.23. (b) T = 760

◦

C. R

relaxation taken below

the elastic limit, R

taken above the elastic limit within the work-hardening range,

ﬁrst relaxation in the steady state range of deformation. The dotted horizontal

line corresponds to the total strain rate ˙ε

before the relaxations. Data from [337]

436 10 Quasicrystals

curves are almost straight and shifted along the stress axis corresponding to

the work-hardening during deformation. There is no sign of recovery, which

is conﬁrmed by the creep test L under constant load in Fig. 10.32a, where

the creep rate continuously decreases. Figure 10.34b shows respective curves

taken from an experiment in the high-temperature range at 760

◦

C. The ﬁrst

relaxation R

is performed below the elastic limit. It is steep, like the curves

at low temperatures, but demonstrates that at high temperatures the spec-

imens deform plastically at a low rate even in the “elastic” range. At low

temperatures, practically no relaxation occurs at much higher stresses. Above

the elastic limit, in the work-hardening range, the relaxation curve R

still

starts with a steep range before it bends to a second range of low slope.

This transition causing an inverse curvature of the relaxation curves is due

to recovery becoming important at low relaxation rates. Curve R

is the ﬁrst

one measured in the range of steady state deformation. The steep initial range

has almost disappeared. Further curves exhibit only the ﬂat part. Strain rate

sensitivity data were always measured from the slope at the beginning of the

curves, corresponding to the strain rate before the relaxations.

Because of the very high values of the work-hardening coeﬃcient in the

work-hardening range of the deformation curves, the work-hardening during

the relaxation tests pronouncedly decreases the relaxation rate, which does

not represent the stress dependence of the activation parameters of the ther-

mally activated process. Therefore, the strain rate sensitivity data have to be

corrected according to

r = r





. (10.11)

With the values of θ and S quoted above, this correction is essential. In

the high-temperature range, the situation is diﬀerent. It was described in

Sect. 10.3.1 that part of the deformation-induced dislocations recovers in the

time scale of usual experiments. Thus, the microstructure may change in

the opposite sign during the stress relaxation tests at high temperatures.

To study these changes, after the original stress relaxation curves labeled

in Fig. 10.32c, “repeated” stress relaxation curves were measured by load-

ing the sample after an original relaxation just up to or below the starting

stress of the original relaxation without reaching the steady state deformation

again. Such repeated relaxation tests are labeled RR

. As shown in Fig. 2.3

in Sect. 2.1, the repeated curves are below the original ones, which indicates

the microstructural changes during the original relaxation tests. These eﬀects

underline the importance of the evolution of the microstructure, i.e., essen-

tially of the dislocation density. The changes in the microstructure have to be

taken into account in evaluating the activation volume via (4.9) by introducing

a correction factor

r ≈

1 − C

, (10.12)

where

=Δln(−˙σ)|

/Δln(−˙σ)|

10.4 Macroscopic Deformation Parameters 437

T (°C)

600

0.0

0.1

0.2

700 800

Fig. 10.35. Dependence of the recovery correction factor C

on the tempera-

ture. ˙ε

=10

−5

−1

(triangles), 10

−4

−1

(squares), ﬁvefold compression axis (full

symbols), twofold compression axis (open symbols). Data from [16]

T (°C)

500

100

200

600 700 800

r (MPa)

Fig. 10.36. Strain rate sensitivity of the ﬂow stress versus temperature. Ful l

symbols: stress relaxation tests during the (initial) work-hardening range, the exper-

imental data are corrected for work-hardening; open symbols: relaxation tests during

steady state deformation, the data are corrected for recovery transients. Strain rate

symbols as in Fig. 10.33. Data from [16, 337]

with the respective quantities being deﬁned in Fig. 2.3. As presented in

Fig. 10.35, this correction factor decreases with decreasing temperature and

(for ˙ =10

−5

−1

) becomes zero at about 625

◦

C, i.e., at the temperature of

the brittle-to-ductile transition. The shift Δσ|

of the beginning of the relax-

ation curves along the stress axis in Fig. 2.3 is almost equal to the yield point

appearing during the transient to the steady state deformation at reloading.

The eﬀect of the evolution of the microstructure on the ﬂow stress and the

determination of the activation parameters at high temperatures are discussed

in detail in [16, 731].

All strain rate sensitivity data are compiled in Fig. 10.36. The data

from the steady state deformation (open symbols) increase with decreasing

temperature and increasing total strain rate. Those obtained from the work-

hardening range (full symbols) show the same tendency but are lower than the

438 10 Quasicrystals

600 700 800

T (°C)

ΔH

(eV)

Fig. 10.37. Activation enthalpy of the deformation of i-Al–Pd–Mn single qua-

sicrystals in the high-temperature range. Symbols as in Fig. 10.33. Data from

[731]

steady state ones. This is partly due to the much lower strain rates but mainly

to diﬀerent mechanisms in the work-hardening and steady state ranges. The

strain rate sensitivity can also be expressed in terms of the stress exponent



= σ/r (4.12). It ranges from about 3 at the high temperature of 800

◦

Cto

about 6 at the brittle-to-ductile transition at 630

◦

C, and to more than 10 in

the low-temperature range without steady state deformation at 550

◦

Activation energies were determined by temperature change tests and

applying (4.14). In the high-temperature range with steady state deformation,

the stress increments were read after steady state was reached again. Both

the temperature sensitivity and the strain rate sensitivity were not corrected

for transient eﬀects since they partly cancel each other [731]. The resulting

activation enthalpy data are plotted in Fig. 10.37. The values are very high,

particularly at high temperatures, which would lead to very low activation

rates when inserted into an Arrhenius equation. As it will be discussed later,

the Gibbs free energies of activation are much lower.

A few temperature change experiments were also performed in the range of

high work-hardening above the elastic limit. The stress increments were read

between relaxation curves at a ﬁxed relaxation rate. They were corrected for

work-hardening. At 564

◦

C, a nominal strain rate of 10

−6

−1

and a stress of

σ = 918 MPa, the activation enthalpy amounts to ΔH ≈ 3 eV. This is much

higher than the values of steady state deformation in Fig. 10.37 at even higher

temperatures.

10.4.2 d-Al–Ni–Co

In contrast to icosahedral Al–Pd–Mn which exhibits isotropic plastic behavior,

decagonal quasicrystals show a pronounced plastic anisotropy as demonstrated

ﬁrst in d-Al–Ni–Co in [721] and afterwards also in d-Al–Cu–Co [733], and d-

Al–Ni–Co again [734, 735]. The quasicrystals were deformed in the A



, A

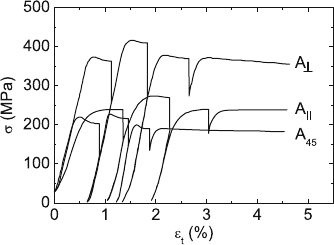
10.4 Macroscopic Deformation Parameters 439

Fig. 10.38. Stress–strain curves of d-Al–15at%Ni–15at%Co at 790

◦

C and a nominal

strain rate of 10

−5

−1

with the A



, A

,andA

⊥

compression axes. The deformation

curves are interrupted by stress relaxation and temperature change experiments.

Data from [735]

and A

⊥

orientations deﬁned in Sect. 10.3.2. The A

⊥

axis is parallel to the P2

quasicrystal orientation. The following data are from d-Al–15at%Ni–15at%Co

[735], the same material as that used for the in situ deformation study in an

HVEM described above.

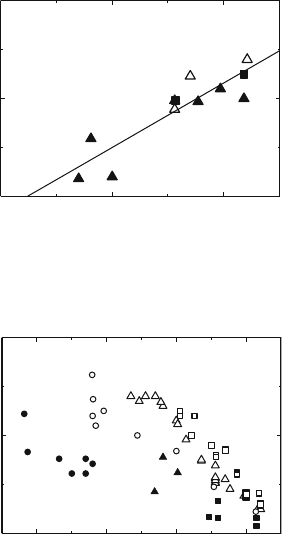
Figure 10.38 presents the stress–strain curves of the three orientations mea-

sured at 790

◦

C. Comparing these curves with those of i-Al–Pd–Mn indicates

that the deformation was performed in the high-temperature range in which

upper and lower yield points clearly develop. The lowest ﬂow stress occurs

in the A

orientation, and the highest one along A

⊥

. The exact relations

between the three orientations depend on the temperature and the crystal

structure within the decagonal phase.

The strain rate sensitivity of the ﬂow stress was determined by stress

relaxation tests. Assuming an orientation factor of 0.5 for all orientations, the

results can be represented by a hyperbolic dependence of the experimental

activation volume on the ﬂow stress, according to V = 185 nm

MPa /σ or by

an experimental stress exponent m



decreasing from about 6 at 700

◦

Cdown

to 4.5 at 850

◦

C, both independent of the orientation of the loading axis.

The temperature dependence of the lower yield points is presented in

Fig. 10.39 for the three orientations. These data are comparable to those of

the steady state ﬂow stresses for i-Al–Pd–Mn. The curves for the A



and A

compression axes do not essentially diﬀer. All three curves have approximately

the same slope except of an anomaly at 730

◦

CinthecurvefortheA



ori-

entation. The activation enthalpies resulting from temperature change tests

and the strain rate sensitivity data are quite independent of the temperature.

For A



,theΔH value of 3.9 eV is considerably lower than that of 5.8 eV for

. Unreasonably high values > 10 eV were obtained for temperatures above

790

◦

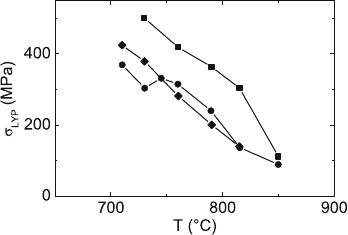
440 10 Quasicrystals

Fig. 10.39. Temperature dependence of the lower yield points of d-Al–15at%Ni–

15at%Co single crystals. A



(circles), A

(diamonds), and A

⊥

orientation (squares).

Data from [735]

In conclusion, the following may be said.

• Quasicrystals can plastically be deformed at temperatures above about

75% of the melting temperature.

• Then, the stress–strain curves exhibit an upper and a lower yield point

followed by a range of almost steady state deformation, sometimes also of

work-softening.

• At lower temperatures, icosahedral Al–Pd–Mn exhibits a transition from

elastic to plastic deformation with a very high work-hardening coeﬃcient.

• The plastic behavior is isotropic for icosahedral quasicrystals but aniso-

tropic for decagonal ones. Markedly higher ﬂow stresses appear for com-

pression perpendicular to the periodic axis.

• The strain rate sensitivity of the ﬂow stress can be characterized by inter-

mediate values of the stress exponent m



in the range between about 3

and 10, with the higher values belonging to lower temperatures.

• At high temperatures, the activation enthalpies are high (6 eV), but they

decrease with decreasing temperature. In d-Al–Ni–Co, the enthalpy for

deformation along the periodic axis is lower than that along an axis

inclined by 45

◦

to it.

10.5 Mechanisms of Dislocation Motion and Plastic

Deformation

Although abundant data have been accumulated about dislocation prop-

erties and plastic deformation of quasicrystals, certain information is still

missing. For example, the stress dependence of the velocity of individual dis-

locations has not been measured yet. Besides, dislocations probably move

in high super- or subsaturations of point defects causing a chemical stress,

which is not proved experimentally. This makes it diﬃcult to separate the

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 441

eﬀects of the dynamics of dislocation motion from those of the development

of the microstructure in which the dislocations move. Accordingly, dislocation

properties and macroscopic deformation data will be discussed in parallel.

10.5.1 Glide or Climb Motion of Dislocations

It’s amazing how long it can take to see the obvious. But of course it’s only

obvious now.

- Ian Stewart, Mathematician

While the deformation curves of diﬀerent quasicrystals measured in the

high-temperature range are quite similar, irrespective of the particular chemi-

cal composition and quasicrystal structure, the ranges of the temperature and

ﬂow stresses scatter widely. However, Takeuchi showed that in a plot of the

upper yield stress versus the temperature, the curves of the diﬀerent icosa-

hedral quasicrystals approach each other, if the axes are suitably normalized

[736]. The scaling relations are σ



= σ

/E and T



= T/(E¯a

), where E is the

bulk modulus, and ¯a, an average of the Goldschmidt diameters of the atoms

constituting the quasicrystal. The possibility of normalizing the temperature

dependence of the ﬂow stress suggests that similar mechanisms control the

plastic deformation in diﬀerent quasicrystalline materials.

Since the ﬁrst direct observation of dislocation motion in an icosahedral

quasicrystal in 1995 in [647], it had been assumed that the main mode of

dislocation motion is glide, although there had been hints that this may be

wrong. As described in Sect. 10.3.1, in situ straining experiments by the group

of Caillard have clearly shown that the motion of dislocations with quasiperi-

odic Burgers vectors is dominated by climb [701,704]. In decagonal Al–Ni–Co

quasicrystals deformed along the tenfold axis, dislocations with a periodic

Burgers vector move also by pure climb (Sect. 10.3.2).

Nevertheless, some combination of climb and glide seems to be possible,

too. In the Videos 10.1 and 10.3, dislocations change the projected width

of their planes of motion without changing the orientation of the traces of

the planes, as also illustrated in Fig. 10.19. For geometrical reasons, this is

only possible by a combination of climb and glide. In the post-mortem TEM

study of samples deformed at 300

◦

C, some dislocations had moved in a mixed

mode [702]. Thus, some contribution of glide to the deformation should also

be possible.

While many dislocations have zero orientation factors for glide and max-

imum ones for climb (set A), there also exist dislocation bands with zero

orientation factors for both glide and climb (set B) like those presented in

Fig. 10.12. As it will be discussed in Sect. 10.5.8, the latter dislocations may

climb under a chemical stress originating from sub- or supersaturations of

point defects, which are generated by the dislocations climbing under the

external stress.

The slip plane of a dislocation is a selected plane of conservative motion

with respect to the volume of the system, i.e., ΔV = 0 in (3.3). The question