Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

442 10 Quasicrystals

arises: what makes the climb plane a preferred plane of dislocation motion in

quasicrystals? This problem is discussed in [687]. The dislocation motion is

considered to occur in a ﬁrst step by the motion of the phonon ﬁeld, charac-

terized by b



, followed by retiling in a second step as illustrated in Fig. 10.10.

The quasicrystalline vectors of forward motion of the dislocation x



and the

line direction ξ



in parallel space have single images x

⊥

and ξ

⊥

in orthogo-

nal space. To respect the tiling matching without overlaps and empty spaces,

a four-dimensional lattice embedded in a subspace (x



⊥

,ξ



,ξ

⊥

)hastobe

kept invariant during the shift of the dislocation by b



.Thisisachievedfor

⊥

⊥ x

⊥

and b

⊥

⊥ ξ

⊥

, implying also that b



⊥ x



and b



⊥ ξ



.Thus,

the mode of dislocation motion maintaining the internal tiling coherent is

pure climb of a pure edge dislocation. This result is illustrated in Fig. 10.40,

based on the simulation of the glide motion in a two-dimensional decagonal

quasicrystal [685]. For glide in the lower part of the ﬁgure, a high density of

phason faults are generated in the wake of the dislocation, which cannot be

retiled by the tiles used for building the regular structure. For climb in the

upper part of the ﬁgure, the quasicrystal halves can be glued together without

overlaps or open spaces by removing or adding so-called worms indicated by

the grey band. Although the climb motion by shifts of b



leaves the lattice

coherent, a phason wall is formed, too, which requires diﬀusional processes to

be annihilated by retiling. Thus, climb should be the easier mode of disloca-

tion motion as long as the dislocation does not move as a perfect dislocation

in equilibrium with its phason ﬁeld. The preference of crystallographic dislo-

cation orientations and planes of motion is possibly supported by particular

core conﬁgurations, e.g., the splitting observed in Fig. 10.17.

In decagonal Al–Ni–Co quasicrystals, the activation enthalpy at compres-

sion along A



is by almost 2 eV lower than that along A

(Sect. 10.4.2).

In the A



orientation, the deformation undoubtedly is carried by climb of

climb

glide

Fig. 10.40. Lattice mismatch produced by climb and glide. The tiling pattern with

the phason wall generated by glide is from [685], copyright Taylor & Francis Ltd.

(1995) (http://www.informaworld.com)

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 443

dislocations with periodic Burgers vectors. In the A

orientation, periodic

screw dislocations dominate, which should have moved preferentially by glide

(Sect. 10.3.2). Although the ﬂow stress is lower for glide, particularly if the dif-

ferent orientation factors for the two loading axes are considered (1 for climb

in A



and 0.5 for glide in A

), the activation enthalpy is higher (for calcu-

lating the activation enthalpy, the orientation factor cancels in (4.14)). Thus,

even for periodic dislocations which do not drag phason faults, the activation

energy of glide is higher than that of climb.

The conﬁrmation of climb as the main mode of dislocation motion makes

it necessary to re-formulate all models of dislocation dynamics and plastic

deformation of quasicrystals.

10.5.2 Components of the Flow Stress

For quasicrystals, in addition to the thermal and athermal components of the

ﬂow stress in (5.15) further contributions have to be considered

σ = σ

+ σ

∗

+ σ

. (10.13)

This equation is written in terms of compressive or tensile stresses since the

appropriate orientation factors are not always clear. The orientation factor m

for glide may assume a maximum value of 0.5. In earlier papers of the author

and his coworkers interpreting the plastic behavior of icosahedral quasicrystals

by glide, e.g., [337,731], a value of m

=0.4 was applied. For determining the

climb force, the extended Peach–Koehler formula (10.10) has to be applied.

Considering only normal stress components, an orientation factor for climb

may be introduced, which for dislocations with b



parallel to the loading

axis moving on a plane perpendicular to it, as it has been observed experi-

mentally, is m

= 1. Since also in the mixed mode of dislocation motion climb

is dominating, m

=0.8 may be taken as a suitable average value.

In (10.13), the ﬁrst term results from the formation of phason walls trailed

behind imperfect dislocations. The second term is the athermal contribution of

long-range dislocation interactions. The third one represents the thermal stress

component which originates from the thermally activated processes control-

ling the dislocation mobility. The last term describes the stress contribution

causing the very strong work-hardening observed at low temperatures above

the elastic limit, e.g., in Figs. 10.32a and b.

10.5.3 Formation of Phason Faults

As outlined in connection with Fig. 10.10, dislocation motion in quasicrystals

is accompanied with the rearrangement of the phason disorder. In computer

simulation experiments, the trailing of phason walls by dislocations gliding at

low temperatures was studied in [699,737]. A recent simulation of glide at high

temperatures in a three-dimensional quasicrystal approximant demonstrates

444 10 Quasicrystals

that the phason wall is relatively sharp directly behind the dislocation but

broadens afterwards [738]. Up to now, there is no theoretical model of the

dislocation motion by climb. The energy per area γ

necessary to create the

phason wall causes a back stress on the moving dislocation given by

= γ





As mentioned in Sect. 10.2.3, the shear stress to trail the phason wall by glide

is very high (τ

≈ (1/27) μ) [685], in accordance with the strongly defective

lattice structure behind the moving dislocation. On the other hand, values

of γ

of the order of magnitude of 25 mJ m

−2

were concluded from splitting

widths of dislocations by climb at 300

◦

C (by analogy with the determination

of the stacking fault energy (3.51)) yielding a back stress of the phason faults

of only about σ

=30MPa/m

[702]. Such a stress would be important above

about 750

◦

C, but is negligible at low temperatures.

The experimental situation about the occurrence of phason walls behind

the moving dislocations is slightly controversial (Sect. 10.3.1). In post-mortem

TEM studies of macroscopically deformed specimens, phason faults have never

been observed above 610

◦

C, whereas during in situ straining in a TEM, they

have sometimes been detected up to about 700

◦

C (Fig. 10.21) or even 750

◦

[712]. From X-ray scattering experiments, the activation energy of the anneal-

ing of phason ﬂuctuations of 2.3 eV is of the order of magnitude of the diﬀusion

energies of Pd and Mn [682], which seems to be reasonable since the process

is connected with diﬀusion. This enables eﬀective phason annealing at 650

◦

which roughly agrees with the in situ annealing study of Fig. 10.22. On the

other hand, the time the phason walls need to disappear during in situ anneal-

ing in the TEM can be described by an activation energy of about 4.3 eV [712],

which is unreasonably high. It is argued in [684] that a dislocation may be

considered to move in the perfect state if the length of the trailed phason wall

l = v

is shorter than about 1 nm. Here, v

is the dislocation velocity, and

, the lifetime of the phason wall. Using the data from [712], this occurs above

800

◦

C for strain rates ≥5 ×10

−5

−1

. Thus, there may be diﬀerent situations

depending on the true activation energy of phason dispersion. Either phason

walls are dragged eﬀectively only below some temperature between about 600

and 650

◦

C, where the respective stress component is unimportant, or the cre-

ation of phason walls has to be considered up to quite high temperatures with

the dragging stress being remarkable. In the ﬁrst case, the onset of (Pd and

Mn) diﬀusion and of phason mobility may cause the transition from brittle to

ductile behavior around about 630

◦

The question is not clear whether the dragging of a phason wall is a ther-

mally activated process, or not. Since there is some similarity to the creation

of a stacking fault, the formation of a phason wall may be considered of ather-

mal character. σ

is then a constant independent of temperature and strain

rate.

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 445

10.5.4 Long-Range Dislocation Interactions

The model of Taylor hardening (5.11) in Sect. 5.2.1 to estimate the long-range

internal stress contribution σ

to the ﬂow stress from the dislocation density

 has to be modiﬁed if the parallel dislocations bypass each other by climb

instead of glide, which is usually considered. With the parallel part b



of the

Burgers vectors of the edge dislocations parallel to the x axis and with the

dislocation lines parallel to z as in Fig. 3.8, the climbing dislocation now moves

in y directiononayz plane with x = x

. The respective stress component of

the dislocation ﬁxed to the origin is the normal stress σ

from the ﬁrst line

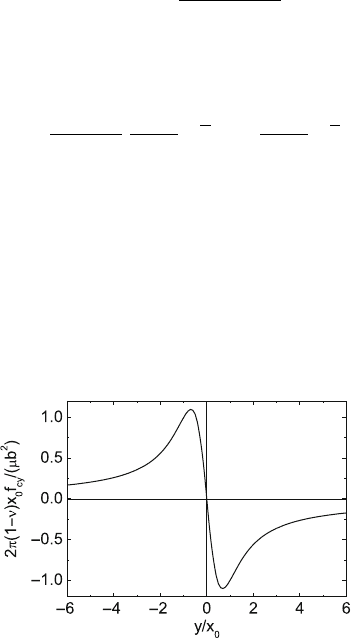
of (3.11). Applying an equivalent normalization as in Fig. 3.14, namely y/x

for the coordinate of motion and 2π(1 −ν)x

/(μb

) for the force, yields the

dependence of the climb force on y/x

plotted in Fig. 10.41. The force is zero

at y = 0 and has extrema at y ≈±0.681 x

. The maximum values are

cym

= ±1.1

μb



2π(1 − ν)y

(10.14)

instead of (3.26) for the glide of screw dislocations. Using again (5.10), the

Taylor equation (5.11) may then read

1.1 × 2π

1 − ν

μb



2πm

√

 = α

μb



2πm

√

. (10.15)

A proper set of parameters may be b



=0.3 nm as in [739], m

=0.8

as suggested above, and α

=2π, which may be justiﬁed by considering

that α

/α

=1.1 × 2/(1 − ν) following from comparing (5.11) with (10.15).

Thus, the mutual interaction between the climbing edge dislocations is much

stronger than that for gliding screws. The temperature dependence of the

shear modulus measured in [740] can be represented by

μ(T )=77.745 GPa − 0.014 GPa K

−1

T − 1.3 × 10

−5

GPa K

−2

, (10.16)

Fig. 10.41. Normalized interaction climb force acting on an edge dislocation

bypassing another one at distance x

by climb

446 10 Quasicrystals

Fig. 10.42. Comparison of diﬀerent components of the ﬂow stress of i-Al–Pd–Mn

single quasicrystals. σ total stress, σ

elastic limit, σ

athermal stress, σ

stress

component causing strong work-hardening. Data from [337]

where T is measured in K. The above data set yields almost the same values

of σ

as those estimated in [337]. The values based on the dislocation density

data of Fig. 5.29 are plotted in Fig. 10.42 as dotted parts of the columns. At

high temperatures, averages of the data from [338] and [337] are used. This

athermal stress component is important at high temperatures in contrast to

the estimation in [739] based on α

=0.7 π.

In the high-temperature range, the dislocations form a three-dimensional

network with segment lengths of L ≈ 0.5 μm (Sect. 10.3.1). For macroscopic

deformation, the segments have to bow out beyond the half-circle (Frank–

Read) conﬁguration in Fig. 3.20c with the radius r = L/2. In analogy to

(3.46), the necessary stress is given by σ

=2Γ/(Lb m

). For the prismatic

edge dislocation loops, the line tension Γ can be replaced by the line energy

of (3.46). With a shear modulus of 48 GPa for 800

◦

C, r

= b



, ν =0.254, and

the constant in the logarithmic factor (3.46) C = −0.59 for the semihexagon,

it follows that σ

= 53 MPa. This is of the same order of magnitude as the

high-temperature value of σ

= 70 MPa in Fig. 10.42. This conﬁrms that the

athermal component of the ﬂow stress from long-range dislocation interactions

should not be neglected at high temperatures. Possibly, also the stress σ

necessary to create the phason walls has to be taken into account in the

athermal stress part.

10.5.5 Activation Parameters of Plastic Deformation

Before discussing possible mechanisms controlling the dislocation mobility

and the thermal component of the ﬂow stress in quasicrystals, the activation

parameters of the deformation, i.e., the activation volume and the Gibbs free

energy of activation, will be presented. In analogy with (4.9), the experimental

activation volume is calculated from the strain rate sensitivity r by

T (°C)

500

1000

1500

600 700 800

σ (MPa)

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 447

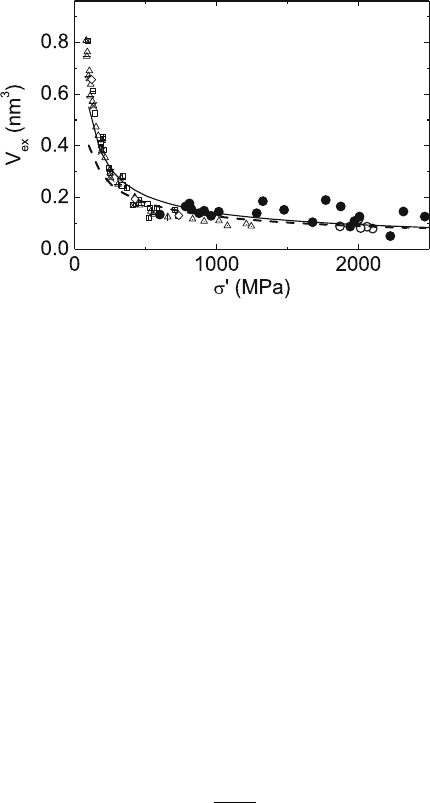
Fig. 10.43. Dependence of the experimental activation volume V

on the reduced

stress σ



. Data from stress relaxations starting from steady state deformation at dif-

ferent strain rates between 10

−5

−1

and 10

−3

−1

(small open symbols)and10

−6

−1

(large open circles) and from the stage of high work-hardening at low temperatures at

−6

−1

(full large circles). Data from [337,731]. Curves: activation volume accord-

ing to the Peierls mechanism (10.18) (full line) and the second term in (10.18)

(broken line)

For comparing the values with the predictions of the models, an orientation

factor has to be considered which, however, is close to unity as discussed in

Sect. 10.5.2. In Fig. 10.43, activation volume data of i-Al–Pd–Mn are plot-

ted versus the applied stress, which are based on the same experiments as

Fig. 10.36. The strain rate sensitivity was measured in stress relaxation tests

under very diﬀerent experimental conditions: diﬀerent temperatures, diﬀerent

strains, diﬀerent starting strain rates of the relaxation tests, and data taken at

diﬀerent stages along the relaxation curves. The data of the high-temperature

range were corrected for recovery using (10.12), and those of the strong work-

hardening range for hardening using (10.11). To correlate the data measured

at diﬀerent temperatures, a reduced stress should be applied



μ(T )

where μ

is the shear modulus at zero temperature, and μ(T )thatattemper-

ature T . The temperature dependence of the shear modulus was taken from

[741], which is similar to (10.16). Except data points measured in the range of

strong work-hardening at low temperatures, all the other data of the plot in

Fig. 10.43 form a single curve. This is quite striking since the conditions of the

measurements were very diﬀerent. Part of the data was obtained near steady

state deformation, and the other part far from steady state during relaxation

tests. Thus, there exists an unequivocal relation between the stress and the

activation volume. It will be shown in Sect. 10.5.8 that this relation describes

the dislocation mobility. A typical value of the experimental activation volume

448 10 Quasicrystals

in the high-temperature range is V

≈ 0.2nm

≈ 13 Ω,whereΩ =0.0157 nm

is the average atomic volume of i-Al–Pd–Mn [714].

The strain rate sensitivity of the ﬂow stress can also be expressed by the

stress exponent m



, according to (4.12). It assumes values between 3 at the

highest temperatures, and up to 10 at low ones in macroscopic tests, and

between about 4 and 7 during the observation of single dislocations in in situ

straining experiments.

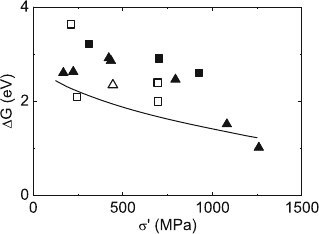
The activation enthalpies ΔH presented in Fig. 10.37 are very high, in

particular for high temperatures. However, the rate of the thermally activated

processes during dislocation motion described by the Arrhenius law (4.7) is

not controlled by ΔH, but by the Gibbs free energy ΔG.Forcrystals,ΔG is

usually calculated from ΔH by applying Schoeck’s formula (4.15), assuming

that the entropy results from the temperature dependence of the shear modu-

lus only. For quasicrystals, there might be other contributions to the entropy,

particularly for the motion of imperfect dislocations, e.g., a conﬁgurational

entropy originating from the change in the phason disorder. However, no the-

oretical treatment is available up to now. Therefore, the data in Fig. 10.44

were calculated by the Schoeck formula and the shear modulus data in [741].

The diﬀerences between ΔG and ΔH are greater than they usually are for

crystals because of the strong temperature dependence of the shear modulus.

The values in Fig. 10.44 yield reasonable rates of thermal activation.

10.5.6 Friction Mechanisms of Dislocation Motion

This section describes possible mechanisms controlling the dislocation mobil-

ity and accordingly the thermal component of the ﬂow stress. These models

have been established for dislocation glide and now have to be modiﬁed to

consider that the dislocations move predominantly by climb. At the turning

point of the discussions, the Scripta Materialia View Point Set No. 30 was

Fig. 10.44. Gibbs free energy of activation of the deformation of i-Al–Pd–Mn single

quasicrystals in the high-temperature range. ˙ε

=10

−5

−1

(triangles), 10

−4

−1

(squares), ﬁvefold compression axis (full symbols), twofold compression axis (open

symbols). Data from [742]. Theoretical curve from the activation energy in (10.17)

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 449

ΔA

(a) (b)

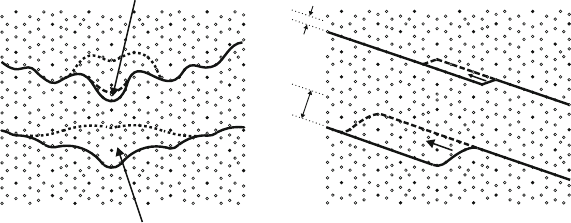
Fig. 10.45. Models of dislocation motion in quasicrystals. (a) Cluster friction

model. Original version [747] (upper part). Reﬁned version [748] (lower part). (b)

Peierls mechanism on the atomic scale (upper part) and on the cluster scale (lower

part). Atom plane after structure model in [656]

published with papers [743–746] on this topic. In this book, the dynamics

of dislocation climb was treated in Sect. 4.10. However, the linearized equa-

tions of the climb velocity cannot be applied under the high stresses which

cause rapid climb. The arguments are mainly that the activation volume of

≈ 13 Ω is too large for climb where V

≈ Ω is expected or, in other terms,

that the stress exponents m



are too high, 3 to 10 instead of 1.

Two types of mechanisms were mainly discussed for glide, lattice friction

mechanisms similar to the Peierls mechanism in crystals and the so-called clus-

ter friction mechanism. The latter was originally suggested in [747] to explain

the experimental values of the activation volume. The maximum experimen-

tal activation volumes plotted in Fig. 10.43 correspond to 50 Ω, which is quite

large for a simple Peierls model. If the orientation factor is considered for glide,

the discrepancy is even larger. As outlined in the upper part of Fig. 10.45a, the

original cluster friction model assumes that the strongly bound Mackay type

clusters (rings of 10 atoms (open circles) around an Mn atom (full circles))

form obstacles to the dislocation motion like localized obstacles, e.g., small

precipitates in crystals (Sect. 4.5).

The dislocation plotted as a full line bows out between these obstacles.

After a single obstacle is overcome individually by thermal activation, the dis-

location may be in the dotted position. The activation area ΔA = l Δd (4.4)

of this process, i.e., the area between the stable equilibrium position before

activation and the unstable equilibrium position after activation, may be the

area between the full and dashed lines in the ﬁgure. Estimates show that with

a diameter of the clusters and a distance between them of about 1 nm, ΔA is

too small to account for the experimental activation volumes. The discrepancy

can be avoided by a reﬁned model [748] assuming that the clusters are not

overcome individually but in a collective way, similarly to the Mott theory

of solution hardening in crystals [210] described in Sect 4.5.2. In this theory,

450 10 Quasicrystals

the clusters are not considered localized (point-like) obstacles, as above, but

extended ones. In the ﬁeld of these extended obstacles of high density, the dis-

location is relatively stiﬀ so that it only weakly bows out. As a consequence,

the obstacles are not overcome individually but in a collective way so that dur-

ing activation the dislocation position changes not only between the central

obstacle and its neighbors but over a wider range, as illustrated in the lower

part of Fig. 10.45a. As a consequence, both the experimental activation volume

V and the activation energy ΔG are much larger than the values of the individ-

ual obstacles. Thus, in the reﬁned model, the clusters are extended weak obsta-

cles to the dislocation motion of high density. The model was conﬁrmed in

the three-dimensional computer simulation study of dislocation glide in [738].

An alternative to the cluster friction model is the Peierls model (Sect. 4.2).

Originally, it was applied to quasicrystals on an atomic scale [744, 749, 750].

It is illustrated in the upper part of Fig. 10.45b. The dislocations form kinks

of height h of the distances between atom rows on the slip plane. Unlike

in crystals, in quasicrystals these distances are not equal but distributed

quasiperiodically. The kinks spread sidewise as indicated by the arrow and

the dashed succeeding position. In the elementary elastic theory of the Peierls

mechanism in crystals [12], the formation energy of a kink ΔF

is given by

(4.26), where W

is the Peierls energy, E

the line energy (or tension) of the

dislocations, and τ

, the Peierls stress at zero temperature. Using character-

istic values of h =0.2nm and τ

≈ 0.03 μ ≈ 1.5 GPa from the computer

simulation in [751], it follows that ΔF

≈ 0.3 eV. In the Peierls model, the

experimental activation energy equals the energy to form a kink pair, i.e.,

2ΔF

, plus the energy of kink motion, which is mostly low. As a result, the

energy obtained from the Peierls model on an atomic scale is too low to explain

the experimental values in Fig. 10.44.

To remove the discrepancy it may be assumed that in quasicrystals, the

kinks form on the cluster level as suggested in [742,752] and illustrated in the

lower part of Fig. 10.45b. In this case, the kink height is approximately equal

to the cluster diameter, h ≈ 0.9nm, so that ΔF

≈ 2.7 eV. The respective

activation energy is now too high, but this may be due to general uncertainties

of the models and the parameters applied.

The Peierls model can quite easily be adapted to the case of dislocation

motion occurring predominantly by climb instead of glide. Instead of the shear

stress τ , the resolved normal stress σ has to be used in the equations. The pro-

cess of the formation of kink pairs is replaced by the formation of jog pairs,

and the spreading of kinks along the dislocations, by the climb motion of

jogs. In their comprehensive modeling of the deformation of icosahedral qua-

sicrystals by climb, Mompiou and Caillard point out that the usual linearized

equations for the climb velocity (4.90) or (4.92) cannot be applied to the high-

temperature deformation of quasicrystals [739]. This is mainly a consequence

of the high applied forces and is expressed, e.g., by the stress exponent m



being clearly higher than unity. They suggest to analogously apply the Peierls

model to the situation of climb with (4.47) for the dislocation velocity v

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 451

with ΔF

∗

fdk

from (4.40) for the formation energy of the jog pair. These are

the equations for “short” dislocations of length λ

, predicting straight dislo-

cations arranged along the Peierls valleys, as it is observed at least at high

temperatures. Since the spreading of kinks by climb involves self-diﬀusion, the

diﬀusion energy ΔF

replaces the kink migration energy. The equation for

the dislocation velocity now reads

∗



exp

⎛

⎝

−

ΔF

+2ΔF

−



∗

μb



/(2π)

⎞

⎠

, (10.17)

with the parameters from Sect. 4.2.2, h being now the height of the jogs,

and ΔF

, their formation energy. The model should be able to account for

the strain rate sensitivity experimentally observed. The activation volume

is then (4.9)

= kT

dlnv

dσ

∗



μb



8πσ

∗

. (10.18)

In Fig. 10.43, the results of (10.18) are plotted for the approximation of σ

∗



, which neglects both σ

and σ

. σ

may be small and the Cottrell–Stokes

law may hold, i.e., σ

is proportional to σ

∗

(Sect. 5.2.2). This would not alter

the functional form of (10.18). However, as in Fig. 10.42 indicated by the

decreasing values of σ

at low temperatures, the Cottrell–Stokes law is violated

at low temperatures. In (10.18), the ﬁrst term stems from the linear stress

dependence of the climb velocity of the jogs, and the second one, from the

stress dependence of the formation energy of the jog pairs. The latter term is

plotted as a dashed line, and the whole activation volume, as a solid one. The

diﬀerence between both curves is the contribution of the climbing motion. It

does not contain adjustable parameters (except the orientation factor assumed

to be close to unity). The correlation between σ and T was obtained from

the temperature dependence of the ﬂow stress in Fig. 10.33. As the curves

in Fig. 10.43 demonstrate, the contribution of climb to the activation volume

is small except at low stresses corresponding to high temperatures or low

strain rates. The parameters of the second term, μ =50GPa,b



=0.3nm,

and h =0.67 nm, are adjusted to ﬁt the high-stress data from steady state

deformation. It turns out that the whole theoretical curve of the activation

volume agrees quite well with the universal experimental curve. In view of

neglecting σ

, this is quite astonishing. An exception are the measuring points

from the range of strong work-hardening at low temperatures (full circles in

Fig. 10.43).

The numerical values above can also be introduced into the expression

of the activation energy in (10.17) to estimate its stress dependence. Assum-

ing that the low values of ΔG at the higher stresses are correct, the curve

in Fig. 10.44 is plotted with ΔF

+2ΔF

= 3 eV to force agreement there.

This is certainly a lower limit. A value of 4 eV may also be realistic. With