Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

452 10 Quasicrystals

decreasing stress, the experimental values of ΔG increase more strongly than

predicted by the model, which may be due to further processes becoming rel-

evant at high temperatures. The energies ΔF

and ΔF

cannot be separated

experimentally. The climb velocity should be determined by the diﬀusion of

the species diﬀusing more slowly, which is Pd or Mn with activation energies

of 2.32 eV [670] and 1.99 eV [713]. Lower diﬀusion energies may result if pipe

diﬀusion plays a role in the climb process. The jog height h =0.67 nm adjusted

to the experimental activation volumes agrees with the Peierls model better

on the cluster scale than on the atomic one. This conclusion had already been

drawn for glide in [742], and for climb in [739]. The elastic energy of the jog

pair of this height should be in the range of several eV as estimated above for

kinks. This would not leave much space for the diﬀusion energy, in accordance

with the results on the activation volume. Unfortunately, more precise data

cannot be given at present.

Takeuchi [753] compared the Peierls model for glide and climb and argued

that in quasicrystals jog pairs can form more easily than kink pairs. However,

the main reason for the predominance of climb in quasicrystals rather is the

diﬀerent structure of the defect walls created by the imperfect dislocations

than the diﬀerence in the elastic properties of kink and jog pairs. A role may

also play the dissociation of the dislocation cores on the climb plane. Split

dislocations have been observed in Fig. 10.17 and were analyzed in [702]. In

many intermetallic alloys, dislocations have complex cores which extend on

planes other than the glide plane, leading to a low glide mobility and to

the inﬂuence of non-glide components of the stress ﬁeld (e.g., [508, 754]). In

particular, the dislocations can undergo a climb dissociation, where glide is

strongly impeded so that climb may be facilitated. Thus, dislocation motion

in quasicrystals may show similarities to that in other intermetallic alloys.

As to the friction models, numerical estimates indicate that the reﬁned

cluster friction model predicts a stress dependence of the activation parame-

ters similar to that of the Peierls model if the same parameters are applied.

That means that the reﬁned cluster friction model and the Peierls model on a

cluster scale are equivalent with respect to the prediction of the macroscopic

deformation data. The cluster friction model is supported by two-dimensional

[751] and three-dimensional molecular dynamics simulations of glide [738,755],

where the dislocations move jerkily between strong spots in the quasicrystal

structure. On the other hand, the Peierls model ﬁts better the straight, crys-

tallographically oriented shape of many dislocations (Fig. 10.18) as well as

the viscous type of dislocation motion. Thus, this model will be preferred in

the following. However, note that coming from low temperatures, at about

530

◦

C at least part of the dislocations strongly bow out between pinning

agents (Fig. 10.14), which is not in agreement with the Peierls model at these

temperatures. The obstacles are most probably kinks in the climbing dislo-

cation lines. The radius of curvature of δ = 50 nm, mentioned in Sect. 10.3.1,

corresponds to a local eﬀective stress of σ

∗

= Γ/(δb) ≈ 240 MPa. In [739],

the change from curved dislocations at lower temperatures to straight ones

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 453

at higher temperatures is explained by a transition in the Peierls model from

the case of “long” dislocations (4.46) to that of “short” ones (4.47). However,

the transition may also be connected with special core conﬁgurations at high

temperatures as in intermetallic alloys.

In decagonal quasicrystals, the activation parameters have values similar

to those in icosahedral ones, the dislocations are also straight and move in a

viscous way preferentially by climb, even those with periodic Burgers vectors.

Thus, the dislocation motion seems to be controlled by the same mechanisms.

10.5.7 Dislocation Kinetics in the High-Temperature Range

Since at the elastic limit the dislocation density is still low, the athermal stress

component σ

in (10.13) is low. Besides, work-hardening has not yet started

(σ

= 0) so that the elastic limit is given by

= σ

+ σ

∗

. (10.19)

The elastic limit is included in the diagram of the stress components in

Fig. 10.42. It shows that in the high-temperature range, say above about

650

◦

C, the total steady state ﬂow stress is given by

σ = σ

+ σ

As discussed in Sect. 10.5.6, the amount of σ

is not clear, especially at high

temperatures. If it can be neglected here, the ﬂow stress at high temperatures

will be

σ = σ

∗

+ σ

as in many crystals. The kinetics of dislocation generation and annihilation as

well as of the resulting ﬂow stress was modeled by a set of constitutive equa-

tions in Sect. 5.2.4 applying a power law for the dependence of the dislocation

velocity on the stress. A similar model for quasicrystals was ﬁrst established

by Guyot and Canova [756], and later on also by Feuerbacher et al. [757]. To

consider work-softening as a speciﬁc feature of quasicrystal deformation, an

order parameter was introduced, which is reduced by plastic strain and recov-

ers in time. The modeling in Sect. 5.2.4 is primarily thought to describe the

(quasi) steady state deformation near the lower yield point. It does not invoke

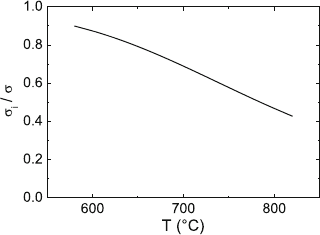
any process speciﬁc to quasicrystals. The results were presented in Fig. 5.29.

The model predicts quite correctly the temperature and the strain rate depen-

dencies of the steady state ﬂow stress as well as the temperature dependence

of the dislocation density down to about 700

◦

C. At low temperatures, the real

dislocation densities are much lower than those predicted by the model. This

agrees with the diﬀerence between the ratio σ

/σ following from the model in

Fig. 10.46 and the respective value of σ

calculated from the measured dislo-

cation densities in Fig. 10.42. Nevertheless, at high temperatures, the plastic

properties of icosahedral Al–Pd–Mn can well be interpreted without taking

into account anything speciﬁc to quasicrystals.

454 10 Quasicrystals

Fig. 10.46. Temperature dependence of σ

/σ at ˙ε =10

−5

−1

after the modeling in

Sect. 5.2.4. Data from [336]

The equations used for the modeling are eﬀectively independent of the

mode of dislocation motion, i.e., glide or climb. Likewise, the kinetics of dislo-

cation generation in crystals and icosahedral quasicrystals seems to be similar.

Like the double-cross slip sources dominating in crystals, the Bardeen–Herring

climb sources, too, do not seem to be localized. A necessary ingredient of the

steady state deformation is the recovery of the dislocation structure, particu-

larly the dislocation density, which in [338] is observed experimentally during

annealing. Besides, the formation of a three-dimensional dislocation network

at high temperatures, as in Fig. 10.11, hints at the action of recovery. It is

also indicated by the inverse curvature of the stress relaxation curve R

Fig. 10.34b. This is the typical recovery-type curve as observed for ZrO

sin-

gle crystals in Fig. 7.34b and interpreted in Sect. 7.3.5. The steep range at

the beginning of the relaxation tests corresponds to the dislocation dynamics

whereas the ﬂat part of the curve is mainly governed by recovery.

The physical processes controlling the dislocation annihilation are still not

clear. If the dislocations move preferentially by climb, the mutual annihilation

of dislocations of opposite sign has to take place by glide, which occurs very

slowly as demonstrated in [705]. It was discussed in Sect. 10.5.1 that strong

structural disorder is generated by glide. To reduce the disorder, extensive

atomic rearrangements are necessary, which certainly involve diﬀusional steps.

At present, it is not yet clear which process of what activation energy con-

trols the recovery. To describe the strong decrease of the steady state ﬂow

stress with increasing temperature, high activation energies of both disloca-

tion mobility ΔG

and recovery ΔG

ann

had to be chosen. They are higher

than the diﬀusion energies of 2–2.3 eV for Pd and Mn [670,713]. The value of

ΔG

= 3 eV agrees with the activation parameters evaluated by the modiﬁed

Peierls model in the preceding section. The supposed stress exponent of the

dislocation mobility of m = 4 is consistent with the exponents observed for

single dislocations during in situ straining (Figs. 10.20 and 10.31) as well as

with those from macroscopic stress relaxation tests (m



=3...6 in the high-

temperature range, Sect. 10.4.1). However, the macroscopic stress exponents

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 455

can conveniently be interpreted by recovery where similar stress exponents are

expected (Sect. 5.2.4). There seems to be a coincidence of the stress exponents

of dislocation mobility with recovery-controlled deformation.

10.5.8 The Climb-Exchange Model

While at high temperatures, the sum of the long-range internal stress compo-

nent σ

and the friction stress σ

∗

of moving dislocations is suﬃcient to interpret

the macroscopic ﬂow stress of i-Al–Pd–Mn, Fig. 10.42 indicates that a further

stress contribution σ

is required to explain the strong work-hardening at low

temperatures. It was suggested in [337] that the hardening results from the

accumulation of phason defects, which cannot anneal out at low temperatures

and which cause hardening instead of softening, which was assumed in other

models.

The strong hardening may also originate from the chemical force due to

the point defect super- or subsaturations, generated by the climbing disloca-

tions. As observed in both icosahedral Al–Pd–Mn and decagonal Al–Ni–Co,

there exist sets of dislocations termed A in Sects. 10.3.1 and 10.3.2, which

climb under high climb forces arising from the external load. Other sets B

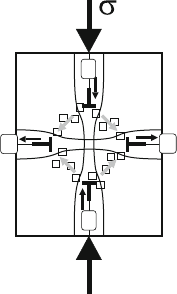
experience zero or small mechanical forces. As illustrated in Fig. 10.47 for the

case of compression, the outward motion of the dislocations of set A occurs by

absorbing vacancies causing a subsaturation, which induces the dislocations

of set B to climb by producing vacancies under a chemical force. The ﬂux of

vacancies is indicated by the open squares and grey arrows. This idea was

ﬁrst put forward by Schall [723] for the motion of periodic and mixed dislo-

cations in d-Al–Ni–Co and later on by Mompiou et al. [702] and Ledig [708]

for i-Al–Pd–Mn. It may be called the climb-exchange model.

Recently, the model was formulated in a quantitative way by Mompiou and

Caillard [739]. The super- or subsaturation of vacancies results in a chemical

A A

Fig. 10.47. Schematic of climb-exchange model for dislocation motion in icosahedral

quasicrystals

456 10 Quasicrystals

climb stress, which is given by the osmotic force f

from (4.84)

b sin β

where β is the character of the dislocation, Ω, the average atomic volume,

, the actual vacancy concentration, and c

, the equilibrium concentration

after (4.76). The chemical stress counteracts the applied stress resulting in

chemical hardening with a strain-hardening coeﬃcient

Δσ

Δε

with Δε being the increment in plastic strain. The latter is given by the

number of absorbed vacancies and, for pure climb, by the area swept by the

dislocations, i.e.,

Δε = c

− c

Note that Δε is negative for compression. Thus, the chemical hardening

coeﬃcient becomes

ln(c

)

− c

Near the elastic limit where c

≈ c

, it may be approximated by

≈

Ωc

These hardening coeﬃcients are very high, higher than the shear modulus.

In [739], they are estimated to agree well with the temperature-depending

initial hardening coeﬃcients observed by Ledig et al. [337] in the range of

strong work-hardening. During in situ straining experiments in a TEM, the

near surfaces can take the role of the dislocation family B so that high super-

or subsaturations of point defects do not develop.

The chemical stress σ

impedes the climb motion of dislocations of the

family A. It is thus identical with the hardening term σ

in (10.13). In addition,

it causes the climb motion of the dislocations of set B, which do not experience

a stress component from the external load. In compressive deformation, these

dislocations emit vacancies which reduce the subsaturation leading the chem-

ical hardening coeﬃcient to decrease. Finally, a steady state develops with

= 0 when equal numbers of vacancies are absorbed and emitted. This is

achieved when



= 

. (10.20)

The dislocations of sets A and B with densities 

and 

move at velocities

(σ − σ

)andv

(σ

). In [739], it is argued that for equal average Burgers

vectors b

= b

during steady state also 

= 

holds. Then, it follows from

(10.20) that v

= v

, which is fulﬁlled for

≈ σ

/2. (10.21)

10.5 Mechanisms of Dislocation Motion and Plastic Deformation 457

is the steady state ﬂow stress. According to these considerations, the defor-

mation behavior of quasicrystals at low temperatures can be interpreted in

the following way. At the elastic limit, only dislocations of set A are moving.

As shown above (10.19)

= σ

+ σ

∗

. (10.22)

∗

is the friction stress of climbing dislocations discussed above in terms of

the modiﬁed Peierls model (10.17).

For the steady state stress, from (10.13), (10.21), and (10.22) and by

neglecting σ

it follows that

= σ

+ σ

=2σ

=2(σ

∗

+ σ

). (10.23)

Thus, the climb-exchange model predicts that the steady state ﬂow stress

equals twice the elastic limit. Neglecting the diﬀerent strain rates in Fig. 10.33,

Mompiou and Caillard claim that this relation is fulﬁlled over the whole

temperature range of this ﬁgure (Fig. 4 in their paper [739]). Indeed, it is

reasonably well fulﬁlled at the lowest temperature of 580

◦

C, where steady

state deformation was achieved at a strain rate of ˙ε =10

−6

−1

. The ﬂow

stress values at lower temperatures (small open circles in Fig. 10.33) belong

to the range of strong work-hardening but not to the steady state. At higher

temperatures, the ratio between σ

and σ

decreases so that σ

< 2σ

.At

700

◦

C, σ

and σ

become equal, and above that temperature no elastic limit

is observed at ˙ε =10

−6

−1

. At a strain rate of 10

−5

−1

, the high-temperature

data represented by the dotted regression curve for the elastic limit and the

dashed one for the steady state ﬂow stress diﬀer by a small constant value.

Only at the lowest temperature of 658

◦

C, the steady state ﬂow stress values

are considerably higher than the elastic limit. It may therefore be concluded

that relation (10.23) is approximately valid at the lowest temperatures where

steady state deformation was achieved but not in the high-temperature range.

The climb-exchange model may also help to interpret the measurements of

the strain rate sensitivity by means of stress relaxation tests. If these tests are

discussed in terms of the power law (4.10) for the strain rate ˙ε,therelaxation

equation (2.7) can be written as

−˙σ = S ˙ε =˙σ

∗m

where all constants are lumped together into ˙σ

. The experimental strain rate

sensitivity r

from (2.8) is then given by

∂ ln ˙ε

∂σ

∂ ln(−˙σ)

∂σ

= m

∂(ln σ

∗

)

∂σ

= m

∂σ

∗

∂σ

∗

Accordingly, the experimental strain rate sensitivity depends on ∂σ

∗

/∂σ,

which deviates from unity if σ

and/or σ

change during the relaxation. It

is usually argued that σ

changes only slowly at the beginning of relaxation

458 10 Quasicrystals

tests. Mompiou and Caillard [739] estimate the change in the stress acting on

the dislocation family B. They conclude that it is zero near the steady state

resulting in ∂σ

∗

/∂σ =1,or

∗

= r.

Thus, considering (4.11), the initial experimental strain rate sensitivity of

relaxation tests starting from steady state deformation represents that of the

dislocation mobility expressed by σ

∗

and m.

After long relaxation times, it is assumed that the recovery of the chemical

stress reduces the stresses acting on both dislocation sets A and B at the same

rate yielding ∂σ

∗

/∂σ =1/2, or

2σ

∗

=2r. (10.24)

Consequently, the experimental strain rate sensitivity increases by a factor of

two after long relaxation times. This behavior is indeed observed, e.g., in the

two-stage relaxation curves R

and R

in Fig. 10.34b. Similar considerations

show that in the range of strong work hardening the correction after (10.11)

has to be applied to obtain the strain rate sensitivity of the dislocation mobil-

ity from r

. In conclusion, after the appropriate corrections, the initial slope

of the relaxation curves should always represent the strain rate sensitivity of

the dislocation mobility. At a ﬁxed temperature, Fig. 10.36 exhibits very dif-

ferent strain rate sensitivities for measurements in the hardening and steady

state ranges. If these data are plotted as the activation volume versus the

temperature-corrected stress as in Fig. 10.43, they ﬁt quite well a single curve

describing the processes of dislocation mobility.

The climb-exchange model is an attractive option to explain the strong

work-hardening at low temperatures without invoking other unknown stress

contributions. It was derived in [739] supposing that the internal stress σ

is small. There is little experimental evidence of the true amount of σ

.The

estimation in Sect. 10.5.4 via (10.15) and the resulting values in Fig. 10.42 are

basedonalargefactorα

. Nevertheless, this is consistent with the stress nec-

essary to bow out segments of the dislocation network. On this basis, σ

cannot

be neglected. This will not basically change the general conclusions from the

model but it will lead to quantitative alterations, e.g., smaller diﬀerences

between σ

and σ

at higher temperatures.

Experimentally, the recovery of the chemical stress causing the two-stage

relaxation curves R

and R

in Fig. 10.34b cannot be distinguished from

the recovery of the dislocation structure, which was modeled for the high-

temperature deformation in Sects. 5.2.4 and 10.5.7, and which also results

in the two-stage relaxation curves. On the other hand, there is no sign of

recovery in the range of high work-hardening at low temperatures, where the

climb-exchange model agrees best with the experimental ﬂow stress data. The

relaxation curves in Fig. 10.34a do not exhibit an inverse curvature towards a

10.6 Conclusions on Quasicrystals 459

recovery stage. They are simply shifted to higher stresses indicating the hard-

ening occurring between the relaxation curves. This is conﬁrmed by the creep

curve included in the experiment of Fig. 10.32a, which exhibits a continuously

decreasing creep rate.

Besides, the climb-exchange model ignores the diﬀerent dislocation struc-

tures formed at low and high temperatures. The recovery-type network

structure (Fig. 10.11) forms only at high temperatures. At low ones, the dis-

locations are arranged in typical low-temperature structures of narrow bands

(Figs. 10.12 and 10.15b). Part of the dislocations strongly bows out to radii

of about 50 nm. From the line tension model analogous to (3.38), a shear

modulus at 550

◦

C of 57.4 GPa, b



=0.3 nm, and an orientation factor of 0.8,

there follows a back stress of σ

= 315 MPa. This is at least part of the dif-

ference between the elastic limit and the steady state ﬂow stress, though the

obstacles causing the dislocations to strongly bow out are not yet clear at

all. Thus, the climb exchange model appears as an attractive suggestion to

explain the strong hardening of i-Al–Pd–Mn at low temperatures although

many questions still remain unanswered.

Mompiou and Caillard argue that the climb-exchange model is not

restricted to quasicrystals but may operate also at high temperatures in crys-

talline materials like TiAl and γ/γ



superalloys [758]. Indeed, rapid climb as

a mode of dislocation motion has been observed also in some intermetallics

described above (TiAl, FeAl). As the stress-driven climb motion of one disloca-

tion causes non-equilibrium concentrations of point defects, other dislocations

can climb under the action of the resulting chemical force. Thus, the climb-

exchange model may be of a more general character at high-temperature

deformation.

10.6 Conclusions on Quasicrystals

The following conclusions can be drawn on the dislocation motion and plastic

deformation of quasicrystals.

• Quasicrystals are intermetallic solids with long-range order but without

periodicity (translational symmetry). In contrast to crystals, which are

built by periodically arranging a single unit cell, at least two “unit cells”

called tiles are necessary to form a quasicrystalline structure, in a one-

dimensional quasicrystal they are long and short distances of an irrational

ratio of the Golden Mean. The arrangement of the atoms can be described

in terms of hyperspaces of more than three dimensions, six dimensions

for quasicrystals with icosahedral symmetry, and ﬁve dimensions for those

with decagonal symmetry. Three axes form the real space, which is also

called the physical or parallel space. The remaining axes form the per-

pendicular or orthogonal space. The hyperspace exhibits translational

symmetry. The positions of atoms are obtained by projecting the lattice

sites of the hyperspace onto the axes of the parallel space.

460 10 Quasicrystals

• In addition to the usual defects in crystals, the quasicrystalline order of

the two “unit cells” may be disturbed leading to violations of the so-

called matching rules. Such defects are called phasonic defects or phasons.

Diﬀusion is necessary to anneal out phason defects. This process is called

retiling.

• Dislocations in quasicrystals carry a long-range elastic strain ﬁeld as in

crystals. In addition, they disturb the quasicrystalline order, i.e., they

induce a ﬁeld of phason defects. The Burgers vector B of dislocations can

be deﬁned in the higher-dimensional hyperspace. It can be separated into

a so-called phonon component b



in real space, and a phason component

⊥

in perpendicular space. b



replaces the Burgers vector in crystals and

describes the elastic strain ﬁeld, whereas b

⊥

describes the ﬁeld of phason

defects in the regular quasiperiodic structure around the dislocation lines.

• In situ straining experiments in a TEM at high temperatures have shown

that dislocations in quasicrystals move in a viscous way on well-deﬁned

crystallographic planes. The determination of both the Burgers vectors

and the planes of motion on the same dislocations revealed that the dom-

inating mode of motion is climb. Only during climb, the tiling matching

is respected without overlaps and empty spaces in the quasicrystalline

structure. A combination of climb and glide seems to be possible, too. Dis-

locations with periodic Burgers vectors in decagonal quasicrystals can both

glide and climb. The mobility of the dislocations can best be described by

a double-kink model on the cluster scale adapted to climb. For dislocation

annihilation, glide is necessary.

• At high temperatures, dislocations may move in their perfect state, i.e.,

they carry their phonon and phason ﬁelds. At low temperatures, imperfect

dislocations having only the phonon ﬁeld drag phason walls. The forma-

tion energy of phason walls is probably very high for glide, and low for

climb. The transition temperature between the motion in the perfect and

imperfect states is not clear. It may be between about 610 and 650

◦

C, but

it may also be substantially higher.

• During plastic deformation, dislocation systems are activated with high

orientation factors for climb, and low ones for glide. In addition, disloca-

tions move on systems with zero or near-zero orientation factors for climb

and glide. At high-temperature deformation, three-dimensional networks

of mostly straight, crystallographically oriented dislocations are formed.

At low temperatures, curved dislocations may form narrow bands.

• At high-temperature deformation, the dislocation density increases

strongly during the initial deformation and the upper yield point. After-

wards, it reaches a steady state value or decreases slightly at higher strains.

After the deformation has stopped, the dislocation density recovers.

• Beyond the elastic range, the stress–strain curves of quasicrystals exhibit

a transition to a range of very high work-hardening. The transition

point may be called the elastic limit. At low temperatures (and usual

strain rates), the specimens break at a stress of about 1.6 GPa. At high

10.6 Conclusions on Quasicrystals 461

temperatures, the curves show an upper and a lower yield point followed

by a range of steady state deformation and work-softening at high plastic

strains. The brittle-to-ductile transition is connected with the possibility

to overcome the upper yield point. It depends strongly on the strain rate.

• The rapid work-hardening in the ﬁrst stage of deformation can be explained

by a chemical stress arising from the point defect super- or subsaturation

resulting from the dislocations climbing under the action of the external

stress. In the climb-exchange model, the chemical stress owing to the excess

or deﬁciency concentrations of point defects causes dislocations to climb

which have zero or near-zero orientation factors for glide and climb. The

model predicts that the steady state ﬂow stress is twice the elastic limit.

This condition holds true at low temperatures. High-temperature defor-

mation can be interpreted only by the long-range internal stress between

dislocations and the eﬀective stress due to the dislocation mobility.