Мешалкина Ю.Л., Самсонова В.П. Математическая статистика в почвоведении: Практикум

Подождите немного. Документ загружается.

Отчет 2. Проверка гипотез о типе распределения и о равенстве средних

Студент Неизвестный Н.Н. Кафедра географии.

Вариант 100.

Дата проверки: Подпись преподавателя:

Проверка гипотез о типе распределения

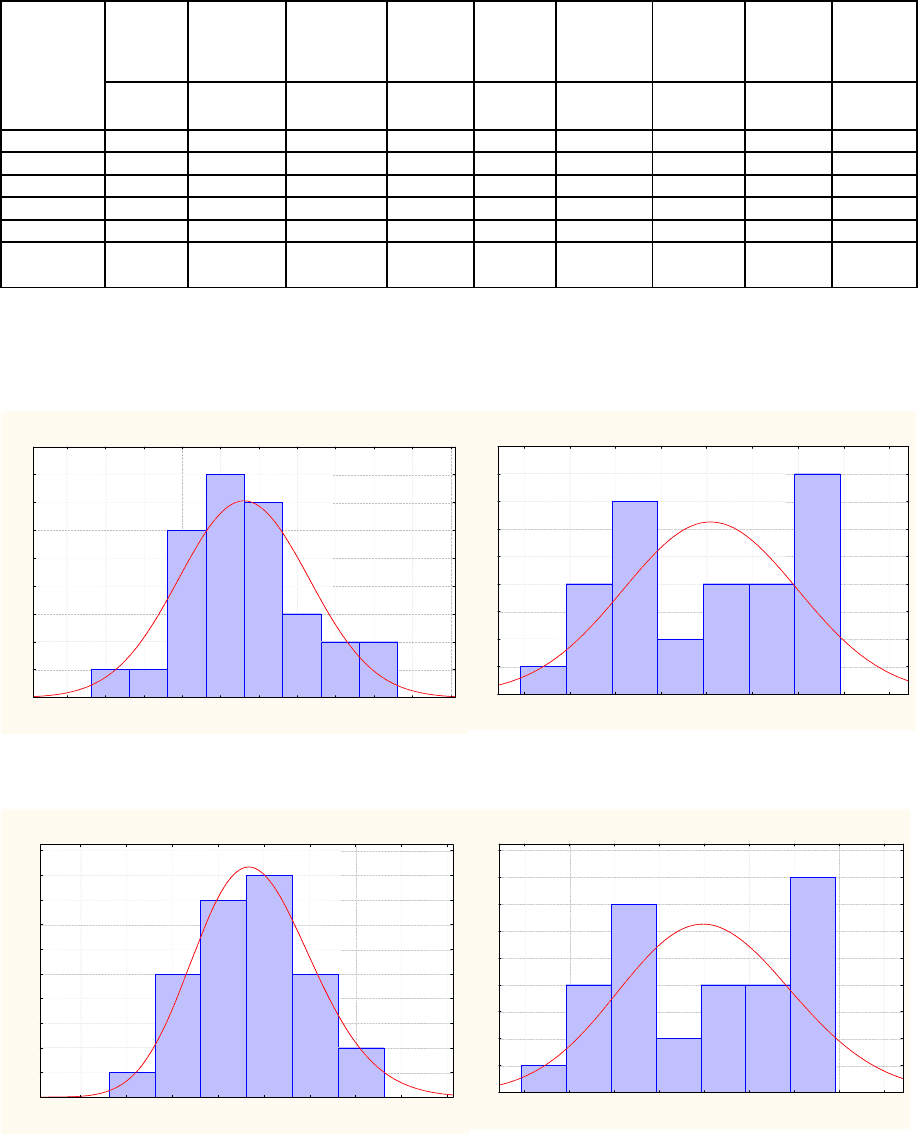
1. Ho: переменная Н1 подчиняется нормальному распределению

Variable: Pole1, Distribution: Normal (Example_for_book.sta) Chi-Square = 0,56717, df = 3, p = 0,90391

Переменная Pole1 ; распределение: Нормальное

Критерий хи-квадрат : 0,57, число ст.св. = 3, p = 0,90

Observed Cumulative Percent Cumul. % Expected Cumulative Percent Cumul. % Observed-

Expected

<= 4,23333 1 1 3,3 3,3 0,7 0,7 2,5 2,5 0,3

4,66667 4 5 13,3 16,7 4,2 4,9 13,9 16,4 -0,2

5,10000 11 16 36,7 53,3 10,2 15,1 33,8 50,2 0,8

5,53333 10 26 33,3 86,7 10,1 25,2 33,7 83,9 -0,1

5,96667 3 29 10,0 96,7 4,1 29,3 13,7 97,6 -1,1

< Infinity

(

Бескон.

)

1 30 3,3 100,0 0,7 30,0 2,4 100,0 0,3

p =0,90 > 0,05 => принимается Ho

Вывод: распределение перем. Pole1 можно аппроксимировать нормальным распределением

Участок 1 Участок 2

2. Проверка на нормальность

p =0,48 > 0,05 => принимается Ho p =0,01< 0,05 => Ho отвергается

3. Проверка на логнормальность

p =0,63 > 0,05 => принимается Ho p =0,02< 0,05 => Ho отвергается

эмпир.

частота

накопл.эмп.

част.

%Верхняя

граница

классов

накопл. % разность

(ожид-

эмп)

накопл.% ожид.

частота

ожид.

накоп.

част.

Variable: H1, Distribution: Normal

Chi-Square test = 0,48530, df = 1 (adjusted) , p = 0,48603

3,90 4,16 4,42 4,68 4,94 5,20 5,46 5,72 5,98 6,24 6,50

Category (upper limits)

No. of observations

V ar iable: H2 , Dis tr ibution: Nor mal

Chi-Square test = 5,47515, df = 1 (adjusted) , p = 0,01929

3,6562 3,7375 3,8187 3,9000 3,9812 4,0625 4,1437 4,2250 4,3062

Category (upper limits)

No. of observations

Variable: H1, Distribution: Log-normal

Chi-Square test = 0,23387, df = 1 (adjusted) , p = 0,62867

3,7813 4,1250 4,4688 4,8125 5,1563 5,5000 5,8438 6,1875 6,5313

Category (upper limits)

No. of observations

Variable: H2, Distribution: Log-normal

Chi-Square test = 5,44993, df = 1 (adjusted) , p = 0,01957

3,6562 3,7375 3,8187 3,9000 3,9812 4,0625 4,1437 4,2250 4,3062

Category ( upper limits)

No. of observations

Отчет 2. (продолжение) Проверка гипотез о типе распределения и о равенстве средних

Студент Неизвестный Н.Н. Кафедра географии.

Вариант 100.

Дата проверки: Подпись преподавателя:

Участок 1 Участок 2

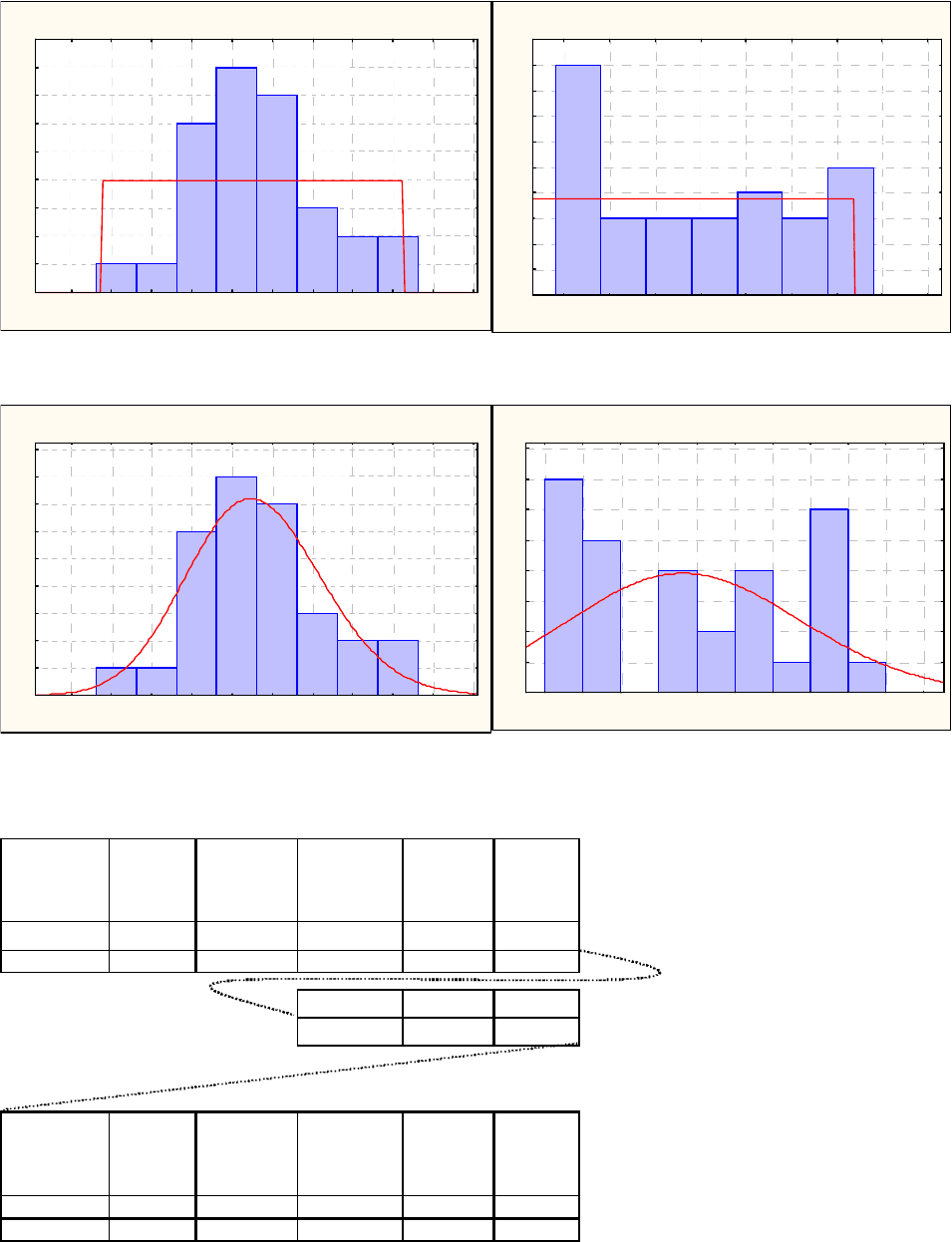
4. Проверка на возможность аппроксимации равномерным распределением

p =0,00 < 0,05 => Ho отвергается p =0,28 > 0,05 => принимается Ho

5. Проверка на возможность аппроксимации гамма распределением

p =0,56 > 0,05 => принимается Ho p =0,22 > 0,05 => принимается Ho

Сравнение средних Ho: генеральное среднее для Н1 = генер-му среднему для Н2

Пере-

менные

Сред-

нее Н1

Среднее

Н2

t-зна-

чение

число

ст. св.

ур. зна-

чимо-

сти

Mean Mean t-value df p

если дисперсии однородны

H1 vs. H2

5,10 3,99 13,01 58,00 0,00

t separ. df p

если дисперсии неоднородны

13,01 36,11 0,00 p =0,00 < 0,05 => Ho отвергается

Среднее Н1 не равно Среднему Н2

Проверка дисперсий на однородность Но: дисперсии однородны

Объем

выборки

Н1

Объем

выборк

и Н2

Ст. откл.

Н1

Ст. откл.

Н2

F- отно-

шение

ур. зна-

чимо-

сти

Valid N Valid N Std.Dev. Std.Dev. F-ratio p

30 30 0,44 0,16 8,03 0,00

p =0,00 < 0,05 => Ho отвергается => дисперсии неоднородны

Va riable: H1, Distribution: Rectan

ular

Chi- Square test = 10,15408, df = 1 (adjus ted) , p = 0,00 144

3, 90 4,1 6 4,42 4,68 4,94 5,20 5, 46 5,72 5,98 6,24 6,50

Category ( up per limits)

No. of obs erv ations

Variable: H2, Distribution: Rectangular

Chi- Square test = 1,12596, df = 1 (adjusted) , p = 0,28864

3,8125 3,8750 3,9375 4,0000 4,0625 4,1250 4,1875 4,2500 4,3125

Category (upper limits)

No. of observations

Variable: H1

Distribution: Gamma

Chi-S

uare test = 0,34286, d f = 1

(

ust ed

)

= 0,55818

3, 90 4,1 6 4,42 4,68 4,94 5,20 5, 46 5,72 5,98 6,24 6,50

Category ( up per limits)

No. of obs erv ations

Variable: H2

Distribution: Gamma

Ch i- S

uare test = 1,51017, df = 1

(

usted

)

= 0,21911

3,80 3,85 3,90 3,95 4,00 4,05 4,10 4,15 4,20 4,25 4,30

Ca teg o r y ( up per lim its )

No. of observations

Отчет 3. Дисперсионный анализ

Студент Неизвестный Н.Н. Кафедра географии.

Вариант 100.

Дата проверки: Подпись преподавателя:

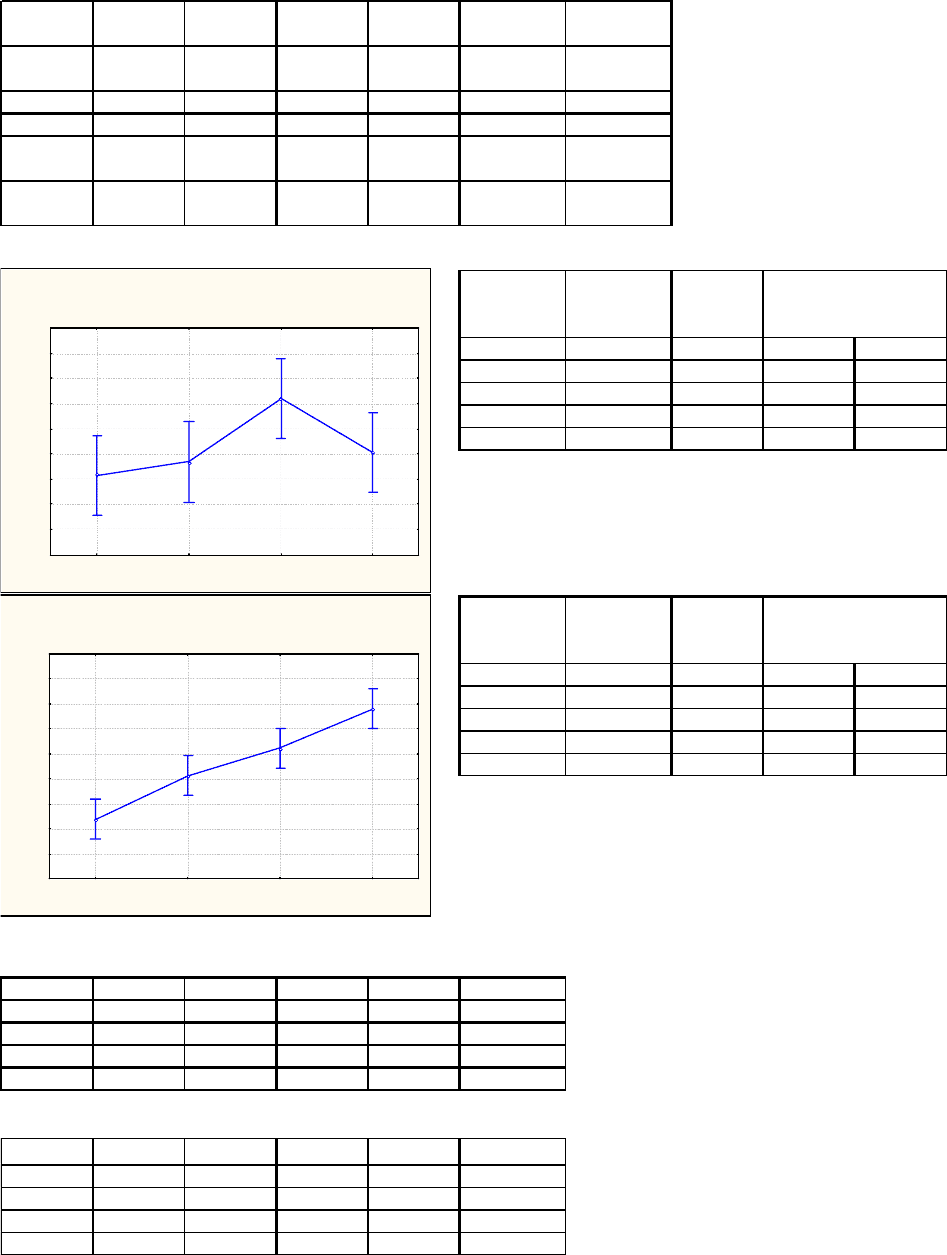
Результаты дисперсионного анализа

Нулевая гипотеза: Средние по градациям фактора равны

Составля

ющие

Сумма

квадратов

Число ст.

свободы

Средний

квадрат F-критерий

Уровень

значимости

SS Degr. of

freedom

MS F p Принимается:

Фактор 1

Herbicids

4246 3 1415 3,146 0,064199

Но:

Фактор 2

Fertilizer 33039 3 11013 24,475

0,000003

Н1:

Взаимо-

действие

Herbicids*F

ertilizer

4186 9 465 1,034 0,455866

Но:

Случ.

составл.

Error 7200 16 450

Выводы: На урожай влияет доза удоб рения

Доза

гербицида

Средний

урожай

кукурузы

Ошибка

среднего

Herbicids Maize yeilds Maize yeilds Maize yeilds Maize yeilds

0 181,5 7,5 165,6 197,4

10 186,8 7,5 170,9 202,7

20 211,9 7,5 196,0 227,8

30 190,6 7,5 174,7 206,5

Доза

удобрения

Средний

урожай

кукурузы

Ошибка

среднего

Fertilizer Maize yeilds Maize yeilds Maize yeilds Maize yeilds

0 147,7 7,5 131,8 163,6

1 182,6 7,5 166,7 198,5

2 204,6 7,5 188,7 220,5

3 235,9 7,5 220,0 251,8

Сравнение средних по градациям Herbicids

Но: среднее по градации 0 и среднее по градации

LSD test -НЗР

фактора гербицид 10 - равны

Herbicids

{1} {2} {3} {4}

1 0 0,628631

0,011394

0,404136

Выводы: отличаются средние 1 и 3,

2 10 0,628631

0,031016

0,720759 2 и 3, 3 и 4

3 20 0,011394 0,031016

0,062661

4 30 0,404136 0,720759 0,062661

Newman-Keuls test -Критерий Ньюмена-Койлса

Herbicids

{1} {2} {3} {4}

1 0 0,628774

0,050390

0,674219 Выводы: отличаются средние 1 и 3,

2 10 0,628774 0,075298 0,720889

3 и 4

3 20 0,050390 0,075298

0,062788

4 30 0,674219 0,720889 0,062788

95% Доверительный

интервал для

среднего

95% Доверительный

интервал для

среднего

Herb icids

;

Unw ei

ht ed Me ans

Cu rrent effec t: F(3, 16)=3,1455, p= ,05420

Effec tive hypoth esis decom pos ition

Ve rtical bars deno te 0,95 co nfiden ce in terva ls

0 102030

Herbicids

150

160

170

180

190

200

210

220

230

240

Ma ize ye ilds

Fertil ize

; U nwe i

hted Means

Current e ffect : F(3, 16)=2 4,475 , p=,00000

E ffect ive hypothe sis d ecom posi tion

Ve rtical bars denot e 0

95 confidence intervals

0123

Fert ilizer

10 0

12 0

14 0

16 0

18 0

20 0

22 0

24 0

26 0

28 0

Maiz e ye ilds

Отчет 3 (продолжение). Дисперсионный анализ

Студент Неизвестный Н.Н. Кафедра географии.

Вариант 100.

Дата проверки: Подпись преподавателя:

Сравнение средних по градациям Fertilizer

Но: среднее по градации 0 и среднее по градации

LSD test -НЗР фактора удобрение 1 равны

{1} {2} {3} {4}

012 3

147,7 182,6 204,6 235,9

0,004592 0,000063 0,000000

Выводы: отличаются средние 1 и 2,

2 1 0,004592 0,054756

0,000126

1 и 3, 1 и 4, 2 и 4, 3 и 4

3 2 0,000063 0,054756

0,009488

4 3 0,000000 0,000126 0,009488

Newman-Keuls test -Критерий Ньюмена-Койлса

Fertilizer

{

}

{

}

{

}

{

}

012 3

147,7 182,6 204,6 235,9

0,004733 0,000319 0,000186

Выводы: отличаются средние 1 и 2,

2 1 0,004733 0,054889

0,000484

1 и 3, 1 и 4, 2 и 4, 3 и 4

3 2 0,000319 0,054889

0,009645

4 3 0,000186 0,000484 0,009645

Изменение средних значений по взаимодействию градаций факторов

Условия применимости дисперсионного анализа:

Проверка однородности дисперсий

Но: дисперсии однородны по градациям фактора …

Харлета Кохрена Бартлетт

Число ст.

свободы

Уровень

значимости

Hartley Cochran Bartlett df p

Effect: "Herbicids" - фактор гербициды

Maize yeilds 2,849967 0,387237 3,045968 3 0,384592 Но:

Effect: "Fertilizer" - фактор удобрение

Maize yeilds

2,502890 0,380452 1,862968 3 0,601329 Но:

Effect: "Herbicids"*"Fertilizer" - взаимодействие

Maize yeilds 43261,21 0,428664 23,54733 15 0,073190 Но:

Her bicids *Fertilizer ; LS Means

Current eff e ct: F( 9, 16)=1,0337, p =,45587

Eff ectiv e hypothes is decomposition

V ertical bars denote 0,95 confidence intervals

Fertiliz er

0 102030

Her bic id s

100

120

140

160

180

200

220

240

260

280

300

320

M aiz e yeilds

Отчет 4. Регрессионный анализ

Студент Неизвестный Н.Н. Кафедра географии. Вариант 100.

Дата проверки: Подпись преподавателя:

Результаты дисперсионного анализа. Регрессия как фактор.

Но: предсказание Y по регрес-

сионной модели не лучше

Sums of

Squares

df Mean

Squares

F p-level

предсказания Y по его среднему

Регрессия

Regress. 42,541 5 8,50816

Остатки

Residual 0,817 14 0,05837

Сумма

Total 43,358

Вывод: Но - отвергается, модель можно считать адекватной и использовать для предсказания Y

Результаты расчета регрессии для переменной : Yield (Example_for_n4)

R= ,99468326 RІ(коэф. детерминации)= ,98939479 скорректированный RІ= ,98740631

F(3,16)=497,56 p<,00000 Стандартная ошибка: 0,18699

станда

тизи

. пе

ем. об ычные перем.

коэфф. станд.ош. коэфф. станд.ош.t-крит. уровень

Intercpt - BETA BETA B коэфф-тов В t(16) значим. Но:

Св.член 4,298 1,676 2,564

0,022

bo=0 Ho

-> H1

Humus 0,122 0,0399 0,906 0,297 3,048

0,009

b1=0 Ho

-> H1

P2O5 1,140 0,0437 0,517 0,020 26,099

0,000

b2=0 Ho

-> H1

pH -0,020 0,0396 -0,077 0,155 -0,493 0,629 b3=0

K2O 0,580 0,0445 0,308 0,024 13,055

0,000

b4=0 Ho

-> H1

NO3 -0,001 0,0395 -0,002 0,139 -0,016 0,987 b5=0 Ho

Yield= 4,29+0,91 * Humus + 0,52 * P2O5 + 0,31*K2O

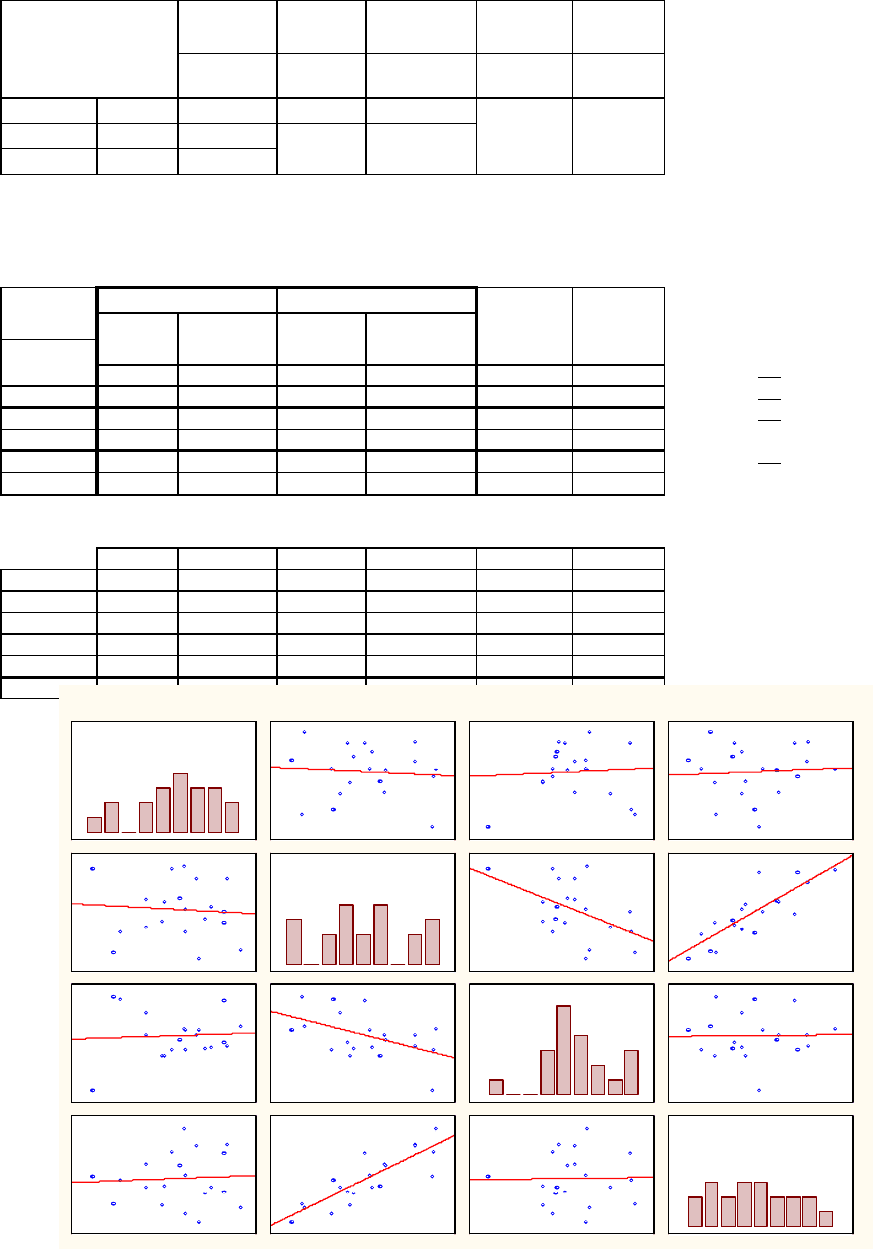
Коэффициенты корреляции между переменными

Humus P2O5 pH K2O NO3 Yield

Humus

1,00

-0,0

0,31 0,06 0,23 0,0

P2O5 -0,08

1,00

-0,16

-0,50

0,11

0,84

0,31 -0,16

1,00

0,21 0,01 -0,04

K2O 0,06

-0,50

0,21

1,00

0,17 0,02

NO3

0,23 0,11 0,01 0,17

1,00

0,2

Yield 0,06

0,84

-0,04 0,02 0,25

1,00

Источник варьиро-

вания

уровень

значим.

0,000

145,76

Сумма

квадр.

числ.ст.

свободы.

средний

квадрат

F-критерий

Correlations (data_zan_4_a.sta 6v*20c)

Humus

K2O

Yield

Отчет 4 (продолжение). Регрессионный анализ

Студент Неизвестный Н.Н. Кафедра географии. Вариант 100.

Дата проверки: Подпись преподавателя:

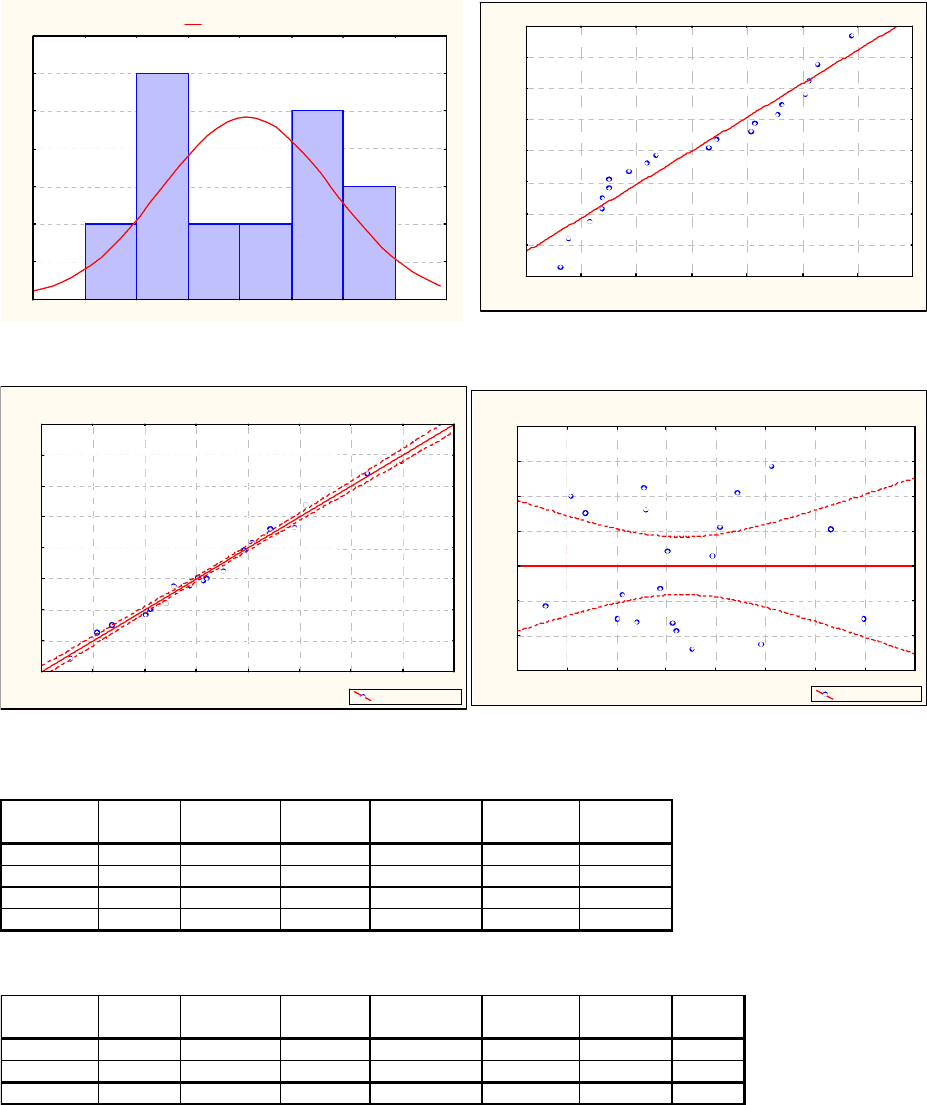
Гистограмма для остатков Остатки на нормальном вероятностном графике

График зависимости наблюдаемых значений урожая График зависимости остатков (ось у) от предсказанных

(ось y) от предсказанных значений (ось x) значений (ось x)

Результаты пошаговой регрессии с вк лючением (Forward)

БЕТА Стд.Ош.

БЕТА

B Стд.Ош. B t(17) p-уров.

Св.член 3,937 1,153 3,413

0,004

P2O5

1,141 0,040 0,517 0,018 28,550

0,000

K2O

0,577 0,040 0,306 0,021 14,459

0,000

Humus

0,116 0,035 0,863 0,259 3,332

0,004

Yield= 3,94 + 0,52 * P2O5 + 0,31* K2O + 0,86 * Humus

Итоги по шагам

Шаг +в /-

ис

Множест.

R-квад

R-квадр.

измен.

F -

вкл/искл

p-уров. Перем.

включ.

P2O5 1 0,8450 0,7140 0,7140 44,9294 0,0000 1

K2O

2 0,9836 0,9675 0,2536 132,7081 0,0000 2

Humus 3 0,9904 0,9808 0,0133 11,0999 0,0042 3

Predic ted v s. O bs erve d V alue s

en dent var iab le: Yield

11 12 13 14 1 5 16 1 7 18 19

Pred icte d V alues

Observed Values

95 % conf idenc e

Normal Probabilit

Plot of Re siduals

-0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4

Re siduals

-2,0

-1,5

-1,0

-0,5

0,0

0,5

1,0

1,5

2,0

Expe cted Normal Value

Predic ted vs. Residual Sc ores

Dependent variable: Y ield

11 12 1 3 14 15 16 17 18 19

Pred icted V alues

-0,3

-0,2

-0,1

0,0

0,1

0,2

0,3

0,4

Residuals

95% c onf idence

Distribution of Raw residuals

Expected Normal

-0 ,4 - 0,3 -0 ,2 -0,1 0,0 0, 1 0,2 0 ,3 0,4

No of obs

Отчет 5. Кластерный анализ

Дата проверки: Подпись преподавателя:

Студент Неизвестный Н.Н. Кафедра географии. Вариант 100.

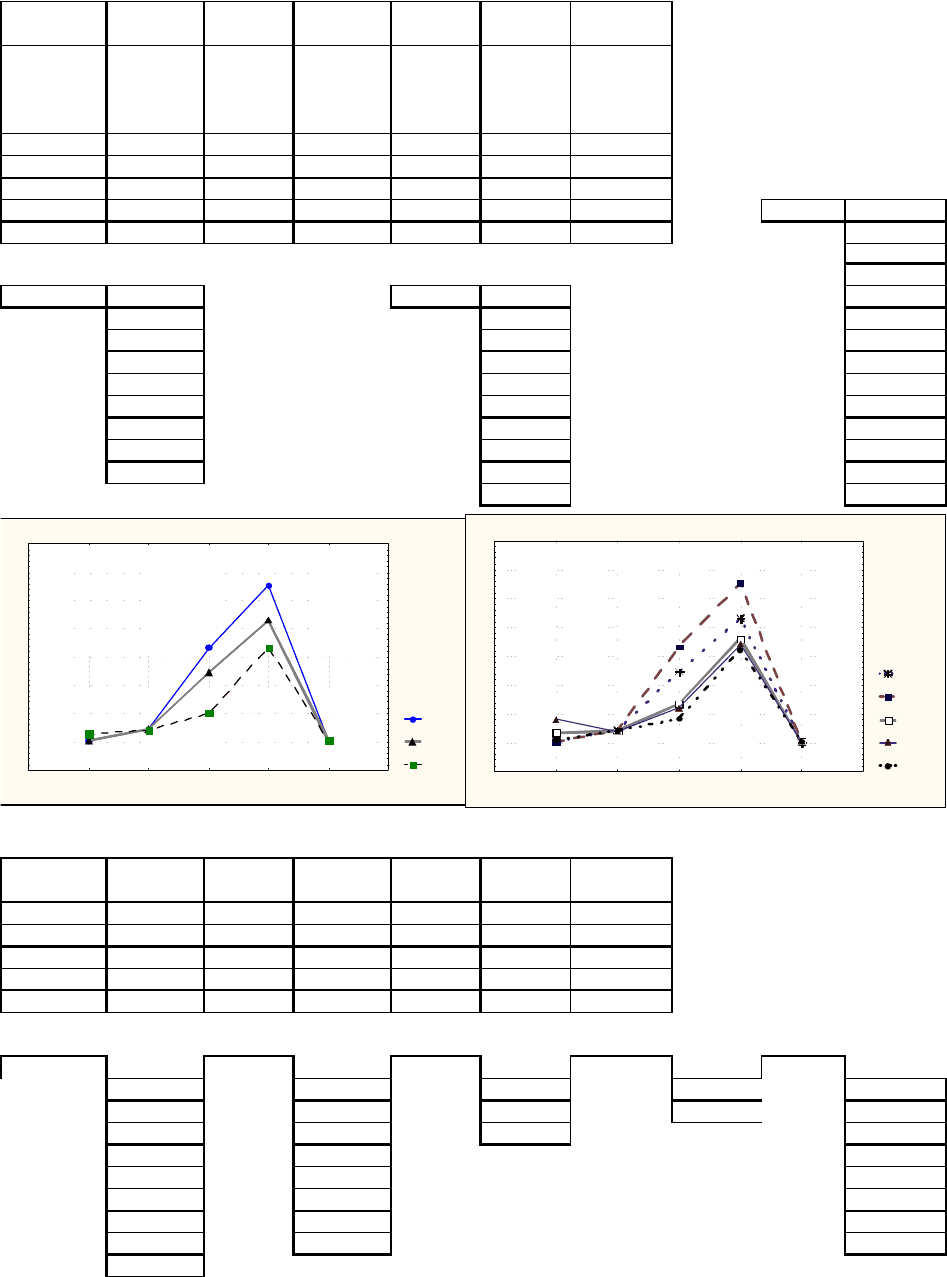
1. Иерархическая классификация

Tree D i ag ra m f or 5 V a r i ab l e s

W ard`s method

Euclidean distances

Linkage D ista nce

100

150

200

250

300

350

G IL PHS V C

Tree Diagram for 5 Variables

Single Linkage

Euclidean distances

LinkageDistance

10 0

12 0

G IL PHS V C

Tree Diagram for 30 Cas es

Single Link age

Euclidean distances

Linkage Distance

A2B

Tree Diagram for 30 Cases

Ward`s method

Euclidean distances

Linkage Distance

100

150

200

250

A2B

Отчет 5 (продолжение). Кластерный анализ

Дата проверки: Подпись преподавателя:

Студент Неизвестный Н.Н. Кафедра географии. Вариант 100.

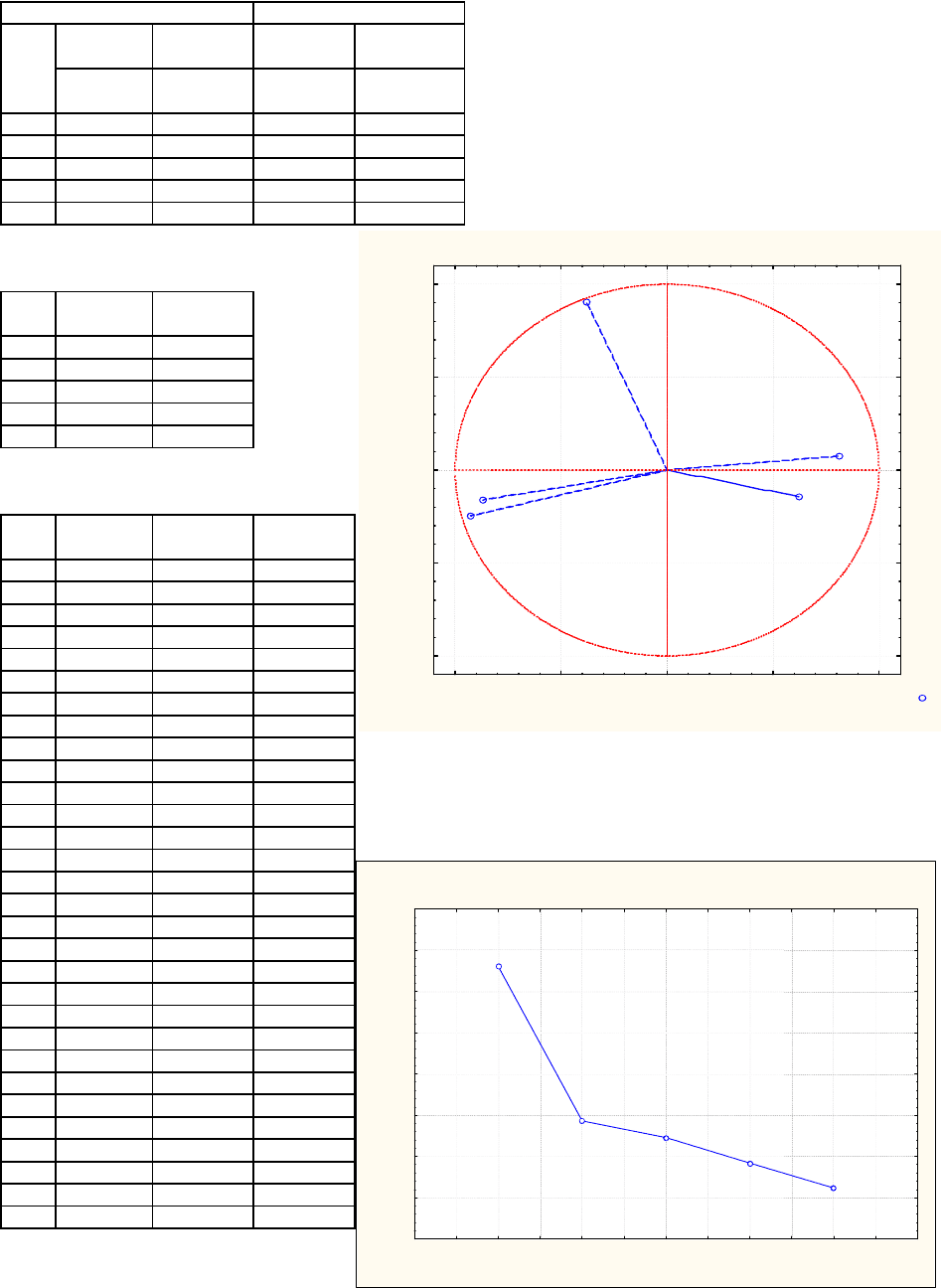
Метод K-средних 3 кластера

Analysis of Variance (pc_kla.sta)- Дисперсионный анализ

Признаки Between Within signif.

SS df SS df F p

Сумма кв.

между

классами

Число ст.

свободы

Сумма кв.

между

классами

Число ст.

свободы

Уровень

значимости

C 41,253422 2 89,541245 27 6,219717 0,0060027

PHS 0,4869745 2 1,8676891 27 3,519941 0,0438099

IL 2881,6445 2 291,72192 27 133,3537 1,015E-14 Members of Cluster 3

G 2422,0554 2 256,64453 27 127,4048 1,774E-14 N=13

V 0,5615084 2 0,5753129 27 13,17607 0,0001016

A1 раз.1

C_1

A2 раз.1

C_2

Объекты 1-го кластера Members of Cluster 2

A1 раз.2

C_6

N=8 N=9

A2 раз.2

C_7

B раз .1

C_4

A2B раз.1

C_3

A1 раз.3

C_11

C раз.1

C_5

A2B раз.2

C_8

A2 раз.3

C_12

B раз .4

C_19

B раз.2

C_9

A2B раз.

C_13

C раз.4

C_20

C раз.2

C_10

A1 раз.4

C_16

B раз .5

C_24

B раз.3

C_14

A2 раз.4

C_17

C раз.5

C_25

C раз.3

C_15

A1 раз.5

C_21

B раз .6

C_29

A2B раз.4

C_18

A2 раз.5

C_22

C раз.6

C_30

A2B раз.5

C_23

A1 раз.6

C_26

A2B раз.6

C_28

A2 раз.6

C_27

5 кластеров

Analysis of Variance (pc_kla.sta)

Between Within signif.

SS df SS df F p

C 122,03867 4 8,7559967 25 87,11078 2,655E-14

PHS 0,5546677 4 1,7999959 25 1,925934 0,1373336

IL 2947,4778 4 225,88867 25 81,55228 5,694E-14

G 2455,95 4 222,75 25 68,90993 3,928E-13

V 0,5645458 4 0,5722755 25 6,165581 0,0013542

Cluster 1 Cluster 2 Cluster 3 Cluster 4 Cluster 5

N=9 N=8 N=3 N=2 N=8

A2B раз .1

C_3

B раз.1

C_4

A1 раз.1

C_1

A1 раз.5

C_21

A2 раз.1

C_2

A2B раз .2

C_8

C раз.1

C_5

A1 раз.2

C_6

A1 раз.6

C_26

A2 раз.2

C_7

B раз .2

C_9

B раз.4

C_19

A1 раз.4

C_16

A1 раз.3

C_11

C раз.2

C_10

C раз.4

C_20

A2 раз.3

C_12

B раз .3

C_14

B раз.5

C_24

A2B раз.

C_13

C раз.3

C_15

C раз.5

C_25

A2 раз.4

C_17

A2B раз .4

C_18

B раз.6

C_29

A2 раз.5

C_22

A2B раз .5

C_23

C раз.6

C_30

A2 раз.6

C_27

A2B раз .6

C_28

Cluster

No. 1

Cluster

No. 2

Cluster

No. 3

Plot of Means for E ach Cluster

Variables

-10

C PHS IL G V

Cluster

No. 1

Cluster

No. 2

Cluster

No. 3

Cluster

No. 4

Cluster

No. 5

Plot of Means for Each C lust er

Variables

-10

C P HS IL G V

Отчет 6. Метод главных компонент

Дата проверки: Подпись преподавателя:

Студент Неизвестный Н.Н. Кафедра географии. Вариант 100.

Кумулятивые

Собствен.

значения

% общей

дисперсии

Собствен.

значения

% общей

дисперсии

Eigenvalue % Total Cumulati-

ve ei

env.

Cumulative

2,804818 56,09637 2,804818 56,0964

0,930753 18,61505 3,735571 74,7114

0,728369 14,56737 4,463940 89,2788

0,420163 8,40325 4,884102 97,6820

0,115898 2,31795 5,000000 100,0000

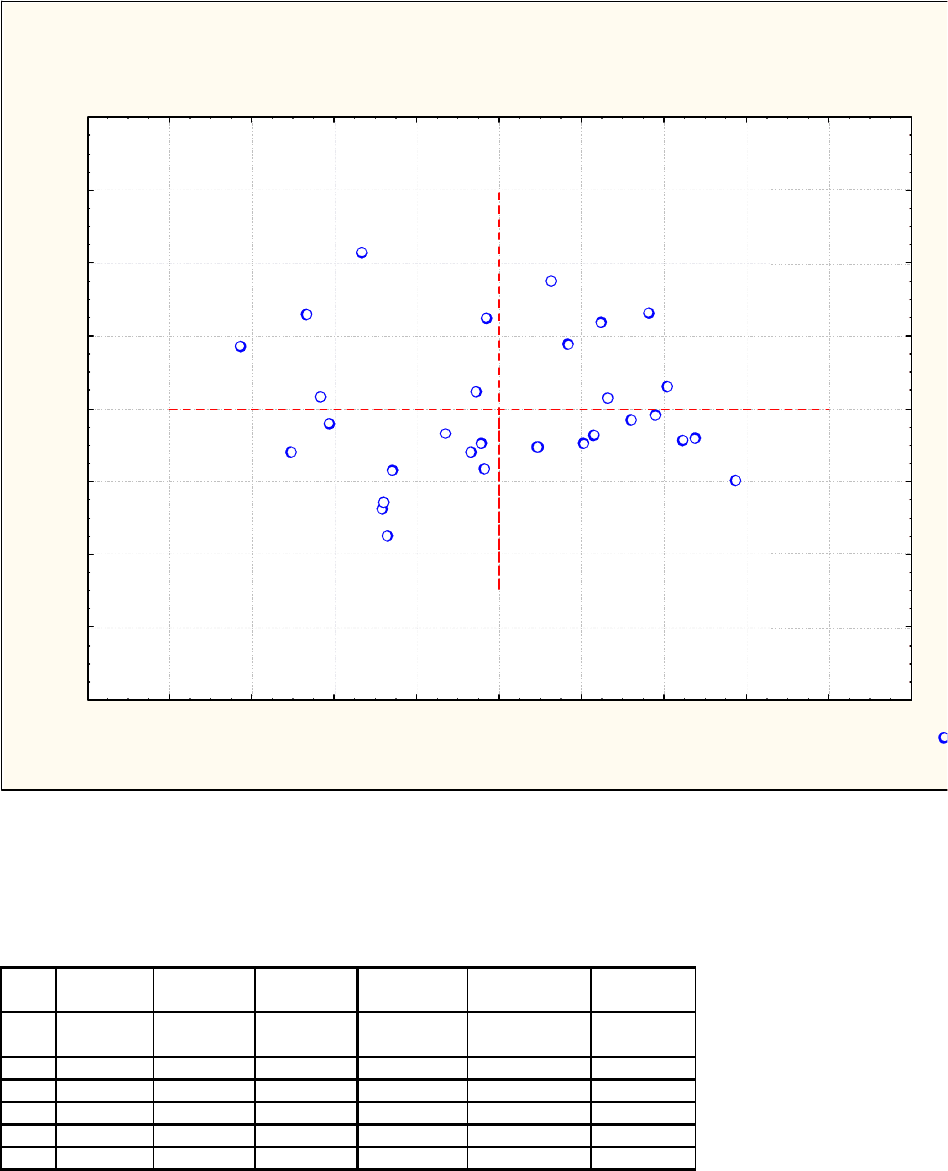
Проекция переменных на 1-у и 2-ю ГК

Факторные координаты переменных

на основе корреляций

Factor 1 Factor 2

ГК1 ГК2

Humus

0,621709 -0,144134

-0,377633 0,904197

-0,927706 -0,245346

Glina

-0,870322 -0,162209

0,810919 0,076803

Координаты наблюдений

при проекции на ГК

ГК1 ГК2 Горизонт

Factor 1 Factor 2

Horizon

1 1,02216 -0,47805 A1

2 0,82514 0,88702 A2

3 -0,22044 -0,46713 A2B

4 -1,29634 -0,85073 B

5 -2,08427 -0,19385 C

6 2,03219 0,30616 A1

7 1,30108 0,14997 A2

8 0,62423 1,76254 A2B

9 -0,19439 -0,81788 B

10 -0,34215 -0,58350 C

11 1,59913 -0,15137 A1

12 1,21859 1,19874 A2 График каменной осыпи

13 -0,17538 1,26837 A2B

14 -2,35219 1,30557 B

15 -2,53471 -0,59746 C

16 1,14668 -0,35424 A1

17 2,36850 -0,40942 A2

18 0,44697 -0,51262 A2B

19 -1,43035 -1,37522 B

20 -1,67325 2,15893 C

21 2,87122 -0,98677 A1

22 1,79848 1,32774 A2

23 -0,66253 -0,32805 A2B

24 -1,40778 -1,28481 B

25 -2,18431 0,17789 C

26 2,22900 -0,41996 A1

27 1,89510 -0,08779 A2

28 -0,29709 0,24098 A2B

29 -1,36040 -1,73988 B

30 -3,16288 0,85479 C

Projection of the variables on the factor-plane ( 1 x 2)

Humus

Glina

-1,0 -0,5 0,0 0,5 1,0

Factor 1 : 56,10%

-1,0

-0,5

0,0

0,5

1,0

Factor 2 : 18,62%

Eigenvalues of correlation matrix

Active variables only

56,10%

18,62%

14,57%

8,40%

2,32%

0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0

Eigenvalue number

-0,5

0,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

Eigenvalue

Отчет 6 (продолжение). МГК и Дискриминантный анализ

Студент Неизвестный Н.Н. Кафедра географии. Вариант 100.

Дата проверки: Подпись преподавателя:

Проекция наблюдений на ГК1 И ГК2

Рез

льтаты дискриминантного анализа

Итоги анализа дискриминантной функции

Число переменных в моделе: 5; Группирующая Horizon (5 grps)

Лямбда Уилкса: ,03214 прибл.. F (20,70)=6,4221 p< ,0002

Уилкса

лямбда

Частная

лямбда F-исключ.

Уровень

значимости

Толерантност

1-Толер.

(R-кв.)

Wilks' Partial F-remove p-level Toler. 1-Toler.

Lambda Lambda -4,21 (R-Sqr.)

Humu

0,104428 0,307773 11,80802 0,000035 0,83096 0,16904

pH 0,038698 0,830533 1,07124 0,395549 0,925299 0,074701

iL 0,043655 0,736232 1,88091 0,151337 0,617279 0,382721

Glina 0,040627 0,791097 1,38635 0,272695 0,608977 0,391023

V 0,049667 0,647108 2,86302 0,048736 0,837269 0,162731

Projection of the cases on the factor-plane ( 1 x 2)

Cases with sum of cosine square >= 0,00

Labelling variable: Horizon

A2B

-5-4-3-2-1012345

Factor 1: 56,10%

-4

-3

-2

-1

Factor 2: 18,62%