Мешалкина Ю.Л., Самсонова В.П. Математическая статистика в почвоведении: Практикум

Подождите немного. Документ загружается.

Результирующая панель содержит информацию о заданных ранее усло-

виях кластерного анализа. Она позволяет оценить качество классификации с

помощью таблицы Дисперсионного анализа (Analysis of variance), получить

таблицу средних значений признаков для кластеров и таблицу расстояний ме-

жду кластерами – Средние кластеров и Евклидовы расстояния (Cluster

means & Euclidean distances), построить графики средних значений для кла-

стеров – График средних (Graph of means), получить описательные стати-

стики для каждого класса (Descriptive statistics for each cluster), получить

таблицу принадлежности объектов к каждому классу Элементы кластеров и

расстояния (Members of each cluster & distances).

Проанализируйте результаты, оценив качество классификации при по-

мощи таблицы дисперсионного анализа (Analysis of variance).

Метод K-средних

3 кластера

Analysis of Variance (pc_kla.sta)- Дисперсионный анализ

Признаки Between Within signif.

SS df SS df F p

Сумма кв.

между

классами

Число ст.

свободы

Общая

сумма кв.

внутри

классов

Число ст.

свободы

Уровень

значимости

C 41,253422 2 89,541245 27 6,219717 0,0060027

PHS 0,4869745 2 1,8676891 27 3,519941 0,0438099

IL 2881,6445 2 291,72192 27 133,3537 1,015E-14

G 2422,0554 2 256,64453 27 127,4048 1,774E-14

V 0,5615084 2 0,5753129 27 13,17607 0,0001016

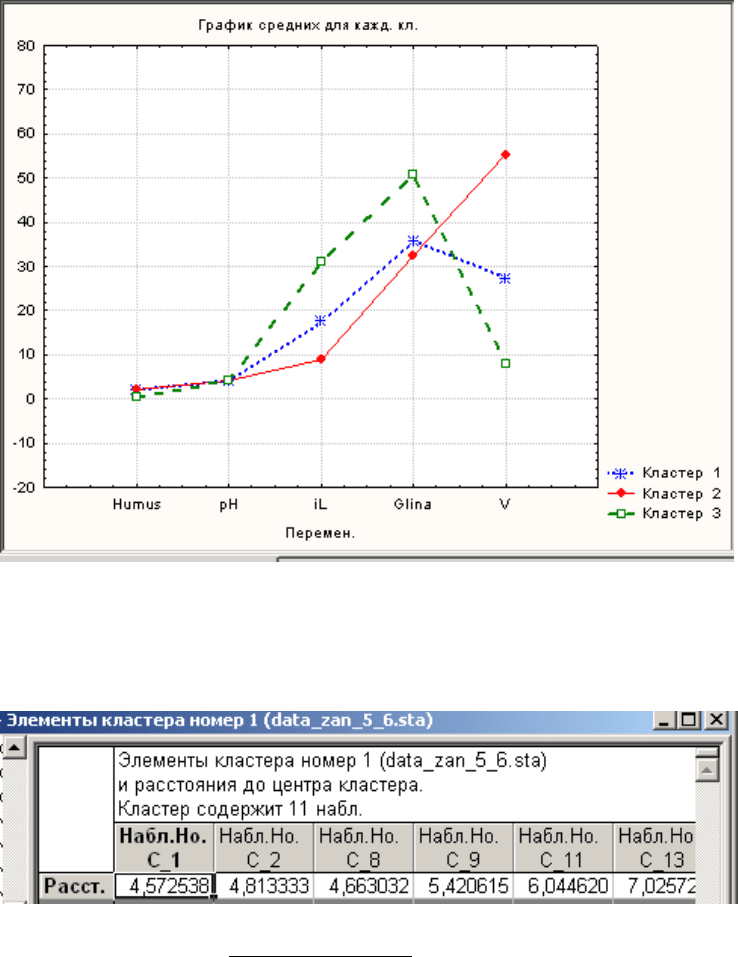
Например, из данной таблицы видно, что для всех почвенных свойств

уровень значимости меньше 0,05 и, следовательно, нулевая гипотеза о равен-

стве средних по выделенным кластерам отвергается. Варьирование между вы-

деленными кластерами превышает внутриклассовое варьирование. Значения

F-статистики, полученные для каждого признака, являются индикатором того,

насколько хорошо соответствующий признак разделяет кластеры.

Постройте график средних и таблицу принадлежности объектов к каж-

дому классу. Результаты сохраните в файле Excel.

При копировании в отчет таблиц принадлежности объектов к кластерам

их необходимо транспонировать и заменить порядковые номера объектов на

названия горизонтов.

Повторите анализ, задав 5 классов. Результаты сохраните в файле Excel.

Распечатайте отчет.

Вопросы к занятию 5

1. Что такое кластерный анализ?

2. Что такое аггломеративные методы кластеризации? Приведите приме-

ры.

3. Что такое итеративные дивизивные методы кластеризации? Приведите

примеры.

4. Что такое расстояние между объектами? Какие виды расстояния между

объектами вы знаете?

5. Какие виды расстояний используются для качественных признаков?

6. Какие методы объединения реализованы в программе STATISTICA?

7. Что такое дендрограмма и как она строится?

8. Для каких случаев, на Ваш взгляд, удобнее вертикальная дендрограмма,

а для каких горизонтальная дендрограмма?

9. На каждой из сохраненных в отчете дендрограмме проведите по 3 сече-

ния. Опишите, как происходит процесс объединения горизонтов в клас-

сы. Какие горизонты попадают в один, а какие в разные кластеры?

10. Чем отличаются кластеры, выделенные методом одиночной связи и ме-

тодом Варда?

11. Какие признаки оказались «ближе», а какие «дальше» для данного мно-

жества горизонтов?

12. В чем заключается принцип работы метода k-средних? К какому типу

методов кластеризации он относится?

13. Как соотносятся результаты работы алгоритма по методу k-средних для

3 и 5 классов?

14. Одинаковое ли разбиение дают разные методы кластеризации для одних

и тех же объектов?

15. Какой метод, на ваш взгляд, дает лучшее разбиение для ваших данных?

Занятие 6 . Метод главных компонент и дискриминантный анализ

ЦЕЛЬ занятия: провести анализ данных методом главных компонент

(МГК); выполнить дискриминантный анализ совокупности данных о горизон-

тах дерново-подзолистой почвы, оценить качество классификации; сравнить

результаты анализов.

МЕТОД ГЛАВНЫХ КОМПОНЕНТ осуществляет переход от исходных

признаков Х

,...,Х

к новой системе координат Y

,...,Y

, называемых главными

компонентами (ГК). ГК представляют собой линейные нормированные ком-

бинации исходных признаков. Они выбираются таким образом, что среди всех

возможных линейных нормированных комбинаций исходных признаков пер-

вая главная компонента Y

обладала наибольшей дисперсией. Вторая главная

компонента имеет наибольшую дисперсию среди всех оставшихся линейных

преобразований, некоррелированных с первой главной компонентой и пер-

пендикулярных первой главной компоненте. Следующие главные компоненты

определяются по аналогичной схеме.

Войдите в пакет STATISTICA (см. занятие №1). В программе

STATISTICA откройте файл данных для 5-6 задания для своего варианта (см.

занятие №3). Данные представляют собой результаты анализов образцов го-

ризонтов, отобранных из 5 разрезов дерново-подзолистых почв Московской

области.

Щелкнув на кнопке Анализ (Statistics), откройте меню и затем выбери-

те раздел Многомерный разведочный анализ (Multivariate Exploratory

Technique), перейдите в раздел Анализ главных компонент и классифика-

ция (Principal Components& Classification Analysis).

На следующей появившейся панели щелкните по кнопке Переменные

(Variables). В разделе Переменные анализа (Variable for analysis) задайте

признаки, по которым будет производиться анализ МГК, - в нашем случае –

гумус, рН, содержание ила и глины, а также степень ненасыщенности. В ка-

честве Группирующей переменной (Grouping variable) задайте перемен-

ную, где закодировано название горизонта (в данном случае Horizon).

Группирующая переменная (Grouping variable- labeling) используется

для задания имен/ меток/обозначений для наблюдений. C помощью группи-

рующей переменной можно также разделить все наблюдения на основные на-

блюдения, по которым проводится анализ, и на вспомогательные наблюдения,

в анализе не участвующие. Для этого нужно одно из значений группирующей

переменной использовать в качестве кода для задания основных наблюдений.

Остальные наблюдения будут считаться вспомогательными наблюдениями.

Здесь же можно задать Вспомогательные переменные (Supplementary

variables), которые не будут участвовать в анализе, но их можно спроектиро-

вать на подпространство главных компонент (ГК), чтобы сделать какие-либо

выводы об этих вспомогательных переменных. В нашем случае – таких пере-

менных нет.

Перейдите на закладку Дополнительно (Advanced).

После того, как переменные заданы, важно принять решение, будет ли

анализ проводится на основе ковариаций, либо корреляций. При анализе, ос-

нованном на матрице ковариаций, на вычисляемые факторы будут влиять раз-

личия вариабельности (изменчивости) переменных, включенных в анализ. В

большинстве случаев, эти различия связаны с различными единицами измере-

ний. В нашем случае анализ будет проводиться на основе корреляционной

матрицы. Поэтому выберите опцию Анализ основан на (Analysis based on)

Корреляциях (Correlations).

Нажмите кнопку OK. Появится новое меню. В информационном поле

диалога представлена общая информация о текущем анализе.

В диалоговом окне установите Число факторов (Numbers of factors)

равным 2. Если в результате, Качество представления (Quality of represen-

tation) получилось меньше 70%, то нужно увеличивать число факторов, пока

качество представления не станет больше или равным 70%.

Перейдите на закладку Переменные (Variables). Выберите клавишу

Факторные координаты (Factor coordinates of variables).

Появится таблица Факторных координат переменных на основе кор-

реляций (Factor coordinates of the variables, based on correlations), в кото-

рой показаны координаты исходных переменных в пространстве главных

компонент (факторов). Так как текущий анализ производится на основе кор-

реляционной матрицы, выводимые результаты можно интерпретировать как

корреляции соответствующих переменных с каждой ГК (с каждым фактором).

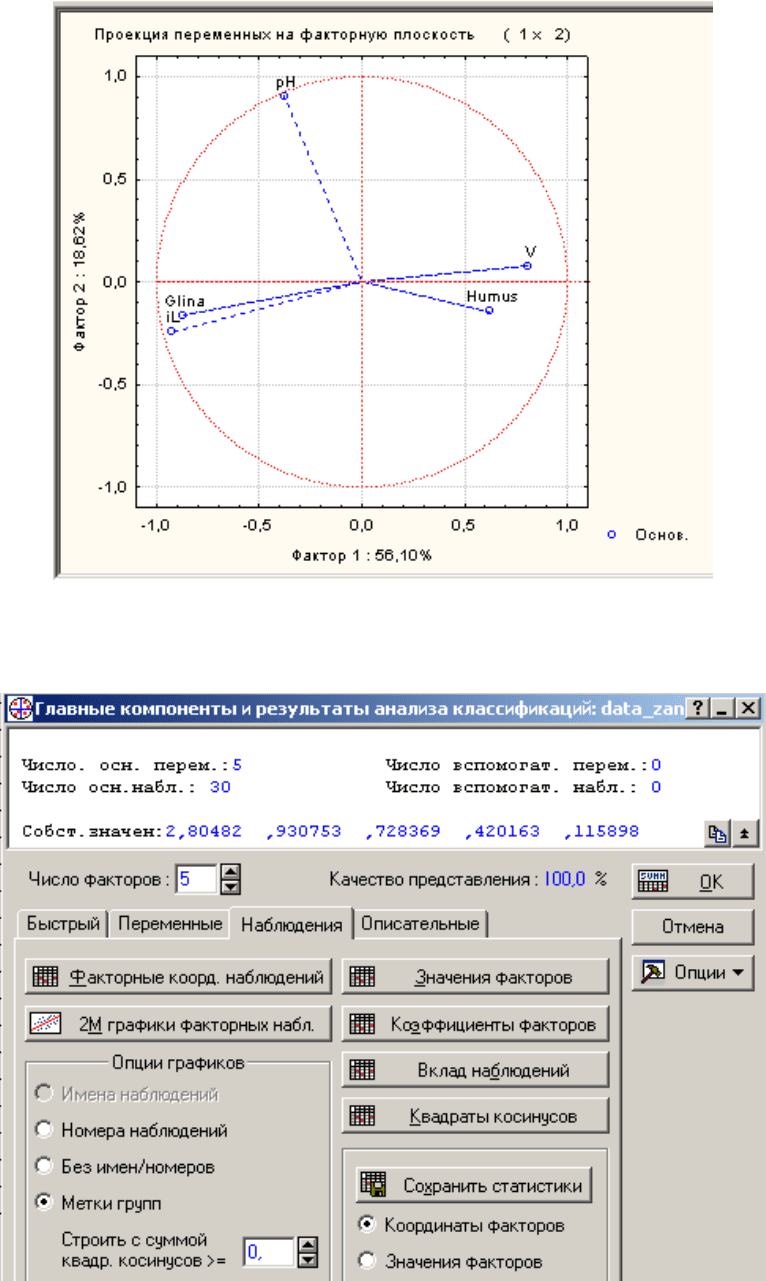
В данном случае, первая ГК (фактор 1) наиболее сильно коррелирует с

переменными Humus, iL, Glina, V; а вторая - с pH.

Нажмите клавишу Собственные значения (Eigenvalues), чтобы по-

строить таблицу собственных значений (собственных чисел). Собственные

значения – это доля от общей дисперсии, соответствующая каждой из компо-

нент. В этой таблице для каждого собственного значения также представлен

процент объясненной дисперсии, кумулятивное собственное значение и куму-

лятивный процент объясненной дисперсии. Собственные значения представ-

лены в порядке убывания, отражая тем самым степень важности соответст-

вующих выделенных факторов для объяснения вариации исходных данных.

Когда анализируются корреляционные матрицы, сумма собственных

значений равна числу переменных, для которых рассчитаны ГК (факторы),

при этом "среднее ожидаемое" собственное значение равно 1. На практике

применяется много критериев для правильного выбора количества ГК. Наибо-

лее простой из них - оставить только те факторы, собственные значения кото-

рых больше или близки к 1. В данном примере, только первые два собствен-

ных значения близки 1 и они объясняют почти 75% общей дисперсии.

Нажмите кнопку График каменистой осыпи (Screeplot). Построенный

график скопируйте в отчет.

Название графика произошло от геологического термина «осыпь», оз-

начающего каменные осколки (лом), лежащие у подножия скал. Этот график

служит для определения числа ГК. На нем отображена последовательность

собственных значений. Нужно определить на этом графике собственное зна-

чение, начиная с которого "горка" теряет свою кривизну и выходит на при-

мерно постоянный уровень. Такое значение и будет искомым числом ГК.

Нажмите кнопку 2М график факторов перем. (Plot var. Factor coordi-

nates, 2D), чтобы построить проекцию переменных на плоскость 2 выбранных

ГК. Скопируйте график в отчет. Так как текущий анализ основан на корреля-

циях, максимальное значение координаты исходной переменной в простран-

стве главных компонент (факторной координаты) не может превысить 1. Кро-

ме того, квадраты всех факторных координат для всех переменных (т.е., квад-

раты корреляций между переменной и всеми факторами) не могут превысить

значения 1. Таким образом, все факторные координаты должны попасть в

единичный круг, выведенный на график. Этот круг является визуальным ин-

дикатором того, насколько хорошо каждая переменная воспроизводится те-

кущим набором выбранных ГК (чем ближе переменная к единичной окружно-

сти, тем лучше она воспроизведена в найденной системе координат).

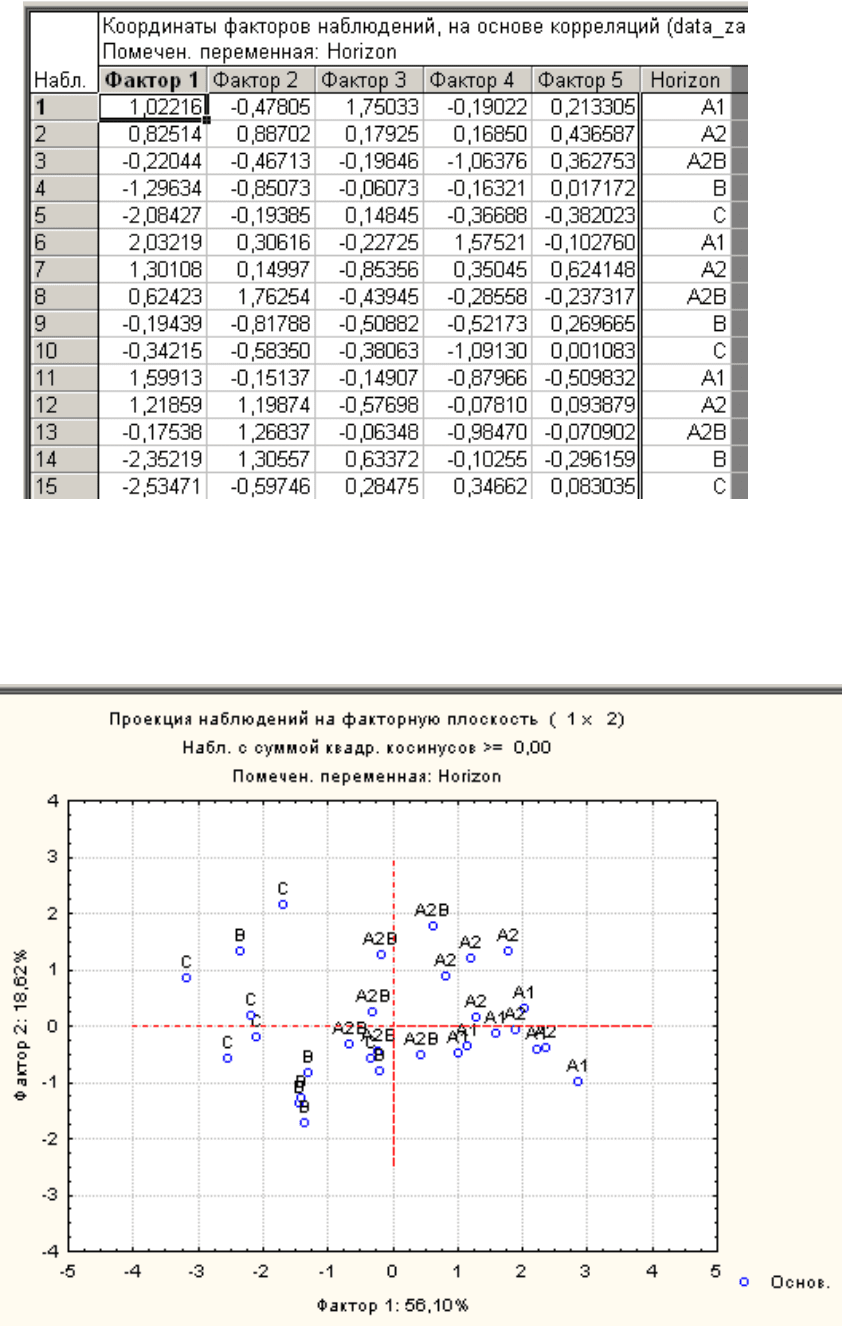
Перейдите на вкладку Наблюдения (Cases). Нажмите кнопку Фак-

торные координаты наблюдений (Factor coordinates of cases).

Появится таблица, где указаны координаты наблюдений на ГК. Интер-

претация факторных координат наблюдений делается с помощью их вкладов в

дисперсию. Первым шагом выделяют наблюдения, которые имеют наиболь-

шие значения вкладов для каждого выбранного фактора. Затем можно вы-

брать подмножество таких наблюдений, чей вклад больше среднего вклада и

т.п. Скопируйте полученную таблицу в отчет.

В этой же вкладке выберите Метки групп (Grouping labels) в группе

опций Опции графиков (Optio ns for plot of factor coord.). Затем нажмите

кнопку 2М графики факторные наблюдения (Plot case factor coordinates,

2D) . Выберите 1-ую и 2-ю ГК. Нажмите ОК.