Мешалкина Ю.Л., Самсонова В.П. Математическая статистика в почвоведении: Практикум

Подождите немного. Документ загружается.

Выберите закладку Дополнительно (Advanced). В появившемся окне

поставите галочку в окне Пошаговая или гребневая регрессия (Advanced

options- stepwise or ridge regression). Проверьте, правильно ли заданы зави-

симые и независимые переменные. Нажмите ОК.

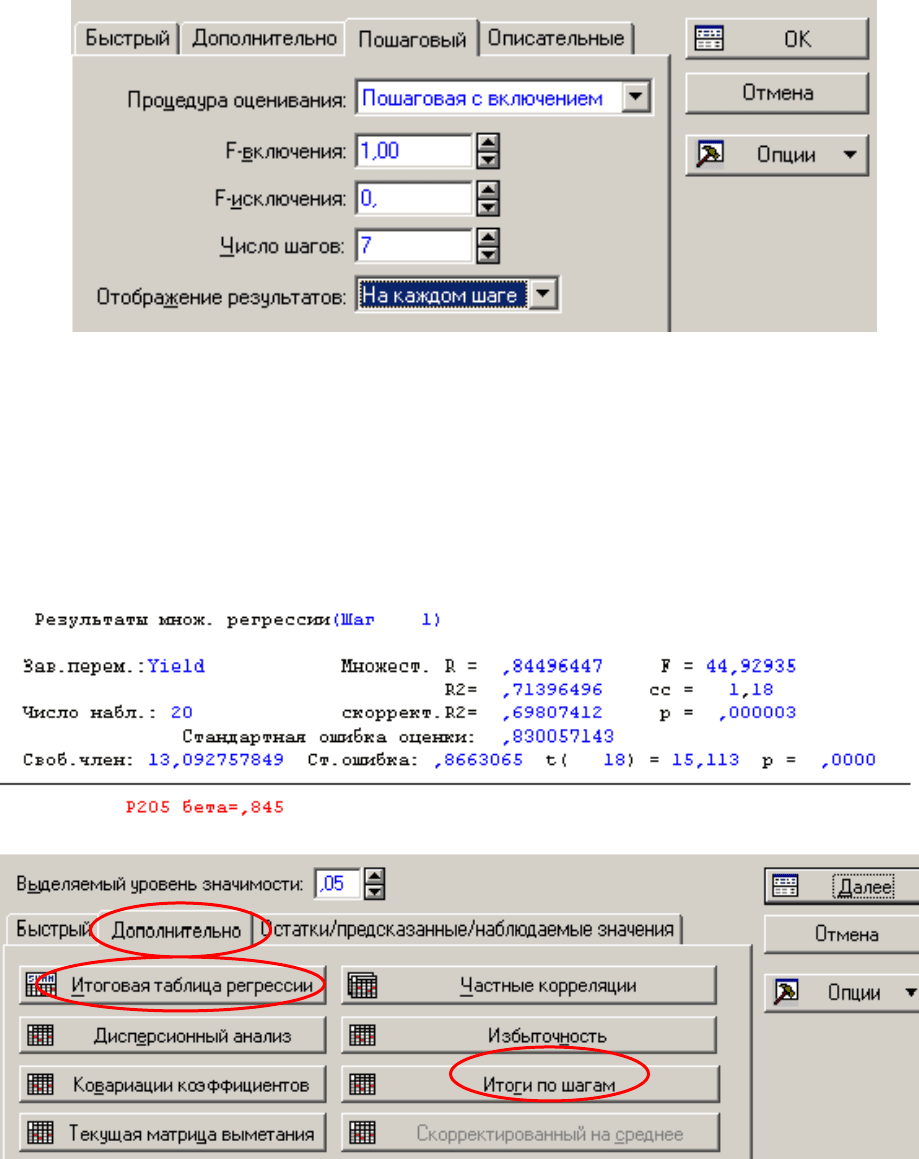
В появившемся меню перейдите на вкладку Пошаговый (Stepwise).

Выберите процедуру Пошаговая с включением (Forward stepwise). В окне

Отображение результатов (Display results) укажите пункт На каждом шаге

(At each step). Нажмите ОК.

Появится панель, суммирующая результаты анализа. На нулевом шаге

не будет выбрано ни одной переменной. Значения коэффициентов R и R

бу-

дут равны нулю.

Нажмите Далее (Next). Появиться новая итоговая таблица, соответст-

вующая первому шагу, на которой, показаны данные для уравнения с одной

переменной, выделенной красным цветом.

На той же вкладке Дополнительно (Advanced) выберите клавишу Ито-

говая таблица регрессии (Summary: regression results). Появится таблица,

аналогичная таблице, полученной при проведении стандартной процедуры

регрессионного анализа, но содержащая одну переменную (в данном случае –

это фосфор) и свободный член.

Вернитесь к меню. На той же вкладке Дополнительно (Advanced) вы-

берите клавишу Итоги по шагам (Stepwise regression summary). В результа-

те будет построена таблица с итогами 1-го шага. Обратите внимание, что

квадрат множественного коэффициента регрессии в данном случае много

меньше полученного для стандартной процедуры. (см. стр.33-34).

Вернитесь к меню и нажмите Далее (Next). Появиться итоговая таблица

для двух переменных (шаг 2). Постройте для уравнения, включающего две

переменные, Итоговую таблицу регрессии (Summary: regression results) и

Итоги по шагам (Stepwise regression summary). Скопируйте таблицы в от-

чет.

Повторите процедуру несколько раз, следя за изменениями итоговой

таблицы и итогов по шагам до тех пор, пока процедура пошаговой регрессии

не закончиться. Копируйте таблицы в отчет. Убедитесь, что информация в

таблицах дублируется. Оставьте таблицы, соответствующие последнему шагу.

Напишите новое уравнение регрессии. В данном случае оно будет вы-

глядеть следующим образом:

Yield [ц/га] = 3,93 [ц/га] + 0,86 [ц/га*%] *Humus [%] + 0, 51 [(ц/га)/ мг-

экв. / 100 г. почвы] * P

[мг-экв. / 100 г. почвы] + 0,31 [(ц/га)/ мг-экв. / 100 г.

почвы] *K

O[мг-экв. / 100 г. почвы] .

Из результирующей таблице итогов по шагам видно, что на первом эта-

пе в уравнение регрессии был включен подвижный фосфор, на втором - калий,

на третьем шаге – гумус. При включении признаков коэффициент множест-

венной корреляции возрастает на втором шаге и практически не изменяется на

третьем.

Вопросы к занятию 4

1. Существует ли линейная зависимость между урожайностью и свойства-

ми почвы?

2. Какие из почвенных свойств влияют на урожайность?

3. Что такое регрессия в стандартизованном (нормализованном) виде? За-

чем используются стандартизированные коэффициенты?

4. Что такое коэффициент множественной корреляции? Чему он равен в

вашем случае?

5. Чему равен коэффициент детерминации? Сильно ли он отличается от

скорректированного коэффициента детерминации?

6. Что такое Intercept? Чему он равен в Вашем случае?

7. Каковы требования к качеству аппроксимации? Как соблюдаются эти

требования в случае множественной линейной регрессии для исследуе-

мых данных?

8. Что такое «остатки»?

9. Можно ли считать остатки нормально распределенными?

10. О чем свидетельствует корреляция между признаками? Что нужно в

этом случае делать?

11. Наблюдается ли мультиколлинеарность для исследуемых данных?

12. Какова связь между дисперсионным и регрессионным анализами?

13. В чем задача пошаговой регрессии?

14. Оцените вклад каждой из независимых переменных в урожай.

15. Выпишите уравнение регрессии, полученное по стандартной процедуре.

Укажите единицы для коэффициентов регрессии и переменных. Посчи-

тайте доверительные интервалы для коэффициентов регрессии.

16. Выпишите уравнение регрессии, полученное при пошаговом анализе

Можно ли считать, что получены разные уравнения?

Занятие 5. Кластерный анализ

ЦЕЛИ данного занятия: провести иерархическую классификацию гори-

зонтов методами одиночной связи и Варда, используя Евклидово расстояние;

провести классификацию переменных этими же методами; выполнить два ва-

рианта классификации объектов методом k-средних, задав в первом случае 3

класса, во втором - 5 классов.

Войдите в пакет STATISTICA (см. занятие №1). В программе

STATISTICA создайте новый файл данных для своего варианта (см. занятие

№3). Введите данные так же, как они даны в таблице данных. Данные пред-

ставляют собой результаты анализов образцов горизонтов, отобранных из 5

разрезов дерново-подзолистых почв Московской области. Сохраните данные.

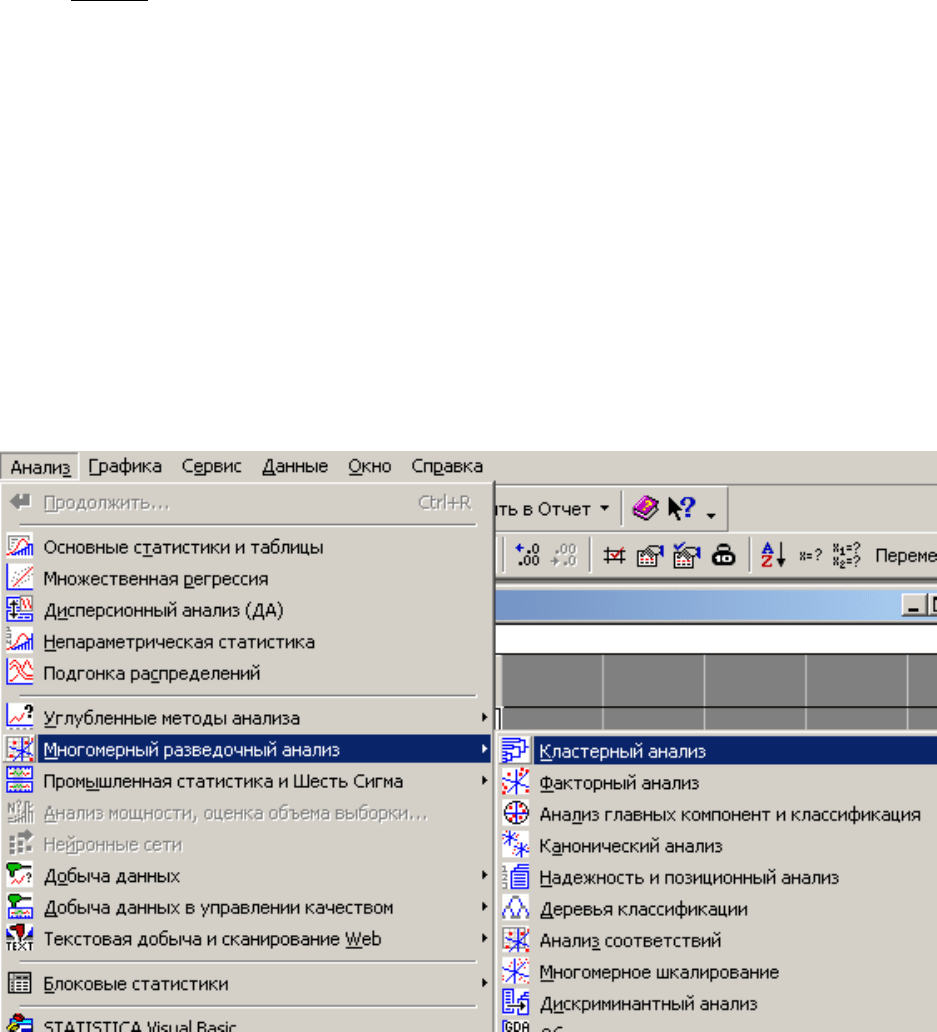
Щелкнув на кнопке Анализ (Statistics), откройте меню и затем выбери-

те раздел Многомерный разведочный анализ (Multivariate Exploratory

Technique), затем перейдите в раздел Кластерный анализ (Cluster Analysis).

Кластерный анализ – это группа методов, используемых для классифи-

кации объектов в относительно однородные группы (кластеры). Эти методы

не являются строгими со статистической точки зрения. Кластерный анализ

используется обычно на начальной стадии исследования, когда не существует

еще гипотез относительно классов, в которые объединяются объекты. Выде-

ляют аггломеративные и итеративные дивизивные методы кластерного анали-

за. Аггломеративные методы кластеризации – это иерархические методы, при

которых на начальном этапе каждый объект находится в отдельном кластере.

На следующих этапах происходит объединение объектов в более крупные

кластеры на основании понижения некоторого порога, например, увеличения

расстояния между объектами. Иными словами, чем выше уровень агрегации,

тем меньше сходства между членами в соответствующем классе. Итеративные

дивизивные методы кластеризации состоят в том, что выполняется разбиение

объектов, объединенных в один или несколько крупных кластеров, на фикси-

рованное число кластеров, как правило, более мелких. При этом образуются

новые кластеры так, чтобы они были настолько различны, насколько это воз-

можно.

Выберите пункт Иерархическая классификация (Joining –tree cluster-

ing) дендрограммы. Нажмите ОК. Для выполнения второй части задания

нужно будет в этом же меню выбрать пункт Кластеризация методом - k-

средних (K-means clustering)).

ИЕРАРХИЧЕСКАЯ КЛАССИФИКАЦИЯ. Выберите закладку Допол-

нительно (Advanced). Выберите переменные (Variables), по которым будет

проводиться анализ (C, PHS, IL, G, V). Обратите внимание, что Файл данных

(Input file) может содержать данные как в исходном виде, так и в виде матри-

цы расстояний (distance matrix). В поле Объекты (Cluster) выберите Наблю-

дения-строки (Cases -rows).

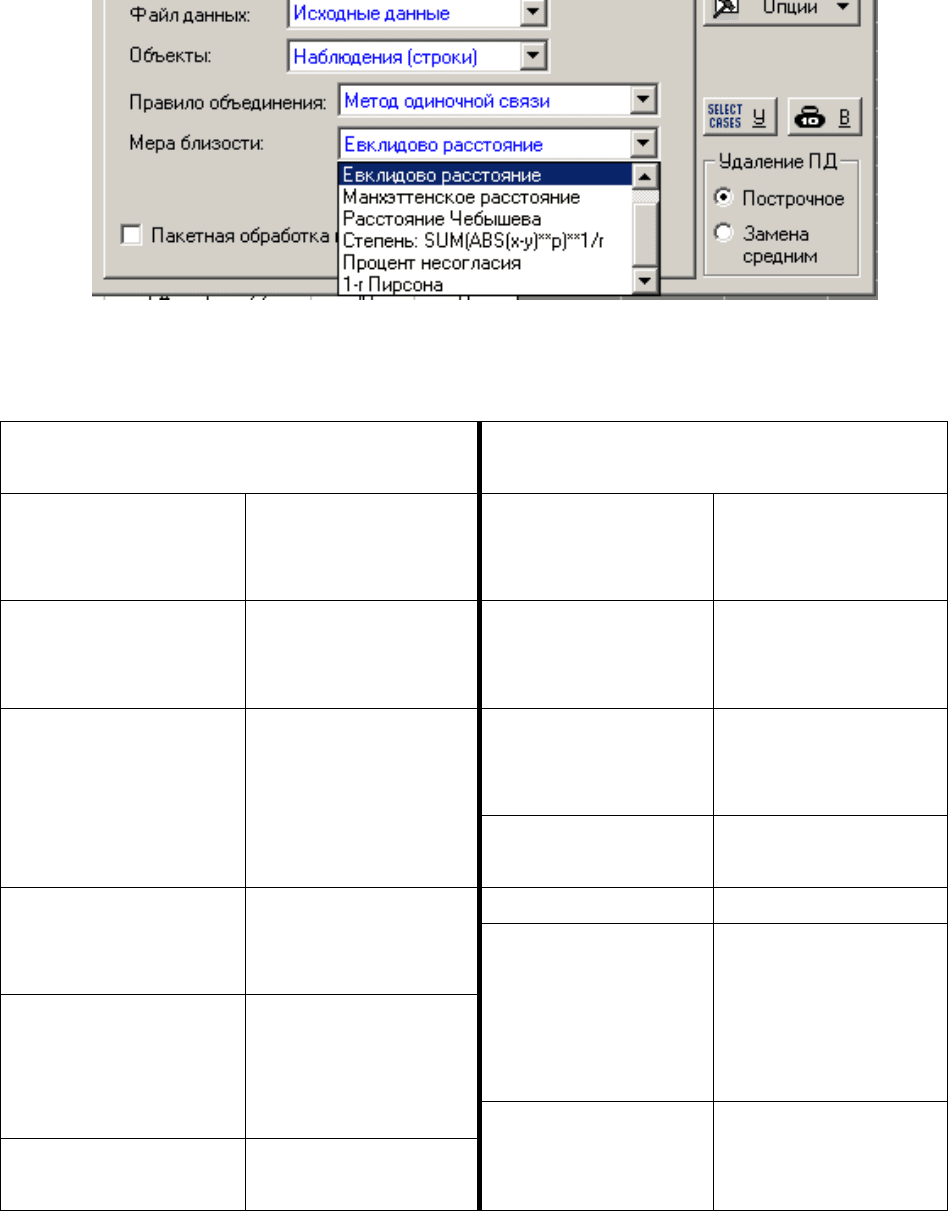
Выберите правило объединения (Amalgamation –linkage rule) и подхо-

дящую Меру близости между объектами (Distance measure).

В таблице приведены возможные варианты перевода названий методов

объединения и мер расстояния.

Joining rule-

Методы объединения

Distance measure –

Меры расстояния

Single linkage Метод одиноч-

ной связи (бли-

жайшего соседа)

Squared Euclidean

distances

Квадрат Евкли-

дова расстояния

Complite linkage Метод полной

связи (дальнего

соседа)

Euclidean dis-

tances

Евклидово рас-

стояние

City (Manchat-

tan)-block

Манхэттенское

расстояние

Unweighted pair

group average

Невзвешенный

метод “средней

связи”, невзве-

шенное попарное

среднее

Chebyshev dis-

tance metric

Расстояние Че-

бышева

Power Степенное Weighted pair

group average

Взвешенный ме-

тод средней свя-

зи

Percent disagree-

ment

Процент несов-

падений (ис-

пользуется для

качественных

признаков)

Weighted centroid

pair group (mе-

dian)

Взвешенный цен-

троидный метод

Ward method Метод Уорда

(Варда)

Pearson r Коэффициент

корреляции (1-r

Пирсона)

Проведите иерархический кластерный анализ Методом одиночной

связи (Single Linkage) с использованием Евклидового расстояния (Euclid-

ean distances). Задав начальные установки, нажмите ОК.

Евклидово расстояние – это геометрическое расстояние в многомерном

пространстве, то есть аналог физического расстояния. Метод одиночной свя-

зи (ближайшего соседа) предполагает, что расстояние между двумя кластера-

ми определяется расстоянием между двумя наиболее близкими объектами

(ближайшими соседями) в сравниваемых кластерах. В результате формируют-

ся кластеры, представленные длинными "цепочками" объектов.

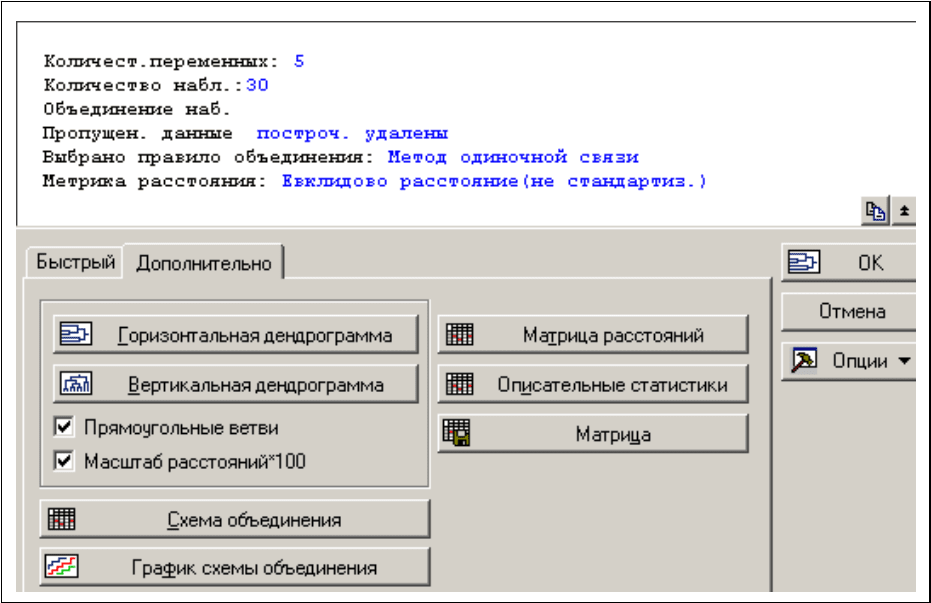
Следующая панель дает информацию о выбранных ранее условиях (чис-

ло случаев, число переменных, число пропусков, способ присоединения и ме-

ра близости).

Появляется возможность построить горизонтально (Horizontal hierar-

chical tree plot) или вертикально (Vertical icicle plot) расположенную дендро-

грамму. Нажмите соответствующую кнопку, чтобы построить каждую из ден-

дрограмм. Посмотрите рисунки.

Для продолжения анализа в нижнем левом углу нажмите на свернутую

панель кластерного анализа (Joining results). По умолчанию дендрограмма

строится с ветвями, соединяющимися под прямыми углами Прямоугольные

ветви (Rectangular branches). Посмотрите, что получится, если значок выбо-

ра снять (дерево получится с острыми углами). Вторая галочка позволяет

масштабировать ось расстояния на рисунке дендрограммы, то есть перейти к

процентам от максимального расстояния (Scale tree to dlink/dmax *100%).

Постройте вертикально расположенную дендрограмму с прямоуголь-

ными ветвями и с масштабированным расстоянием.

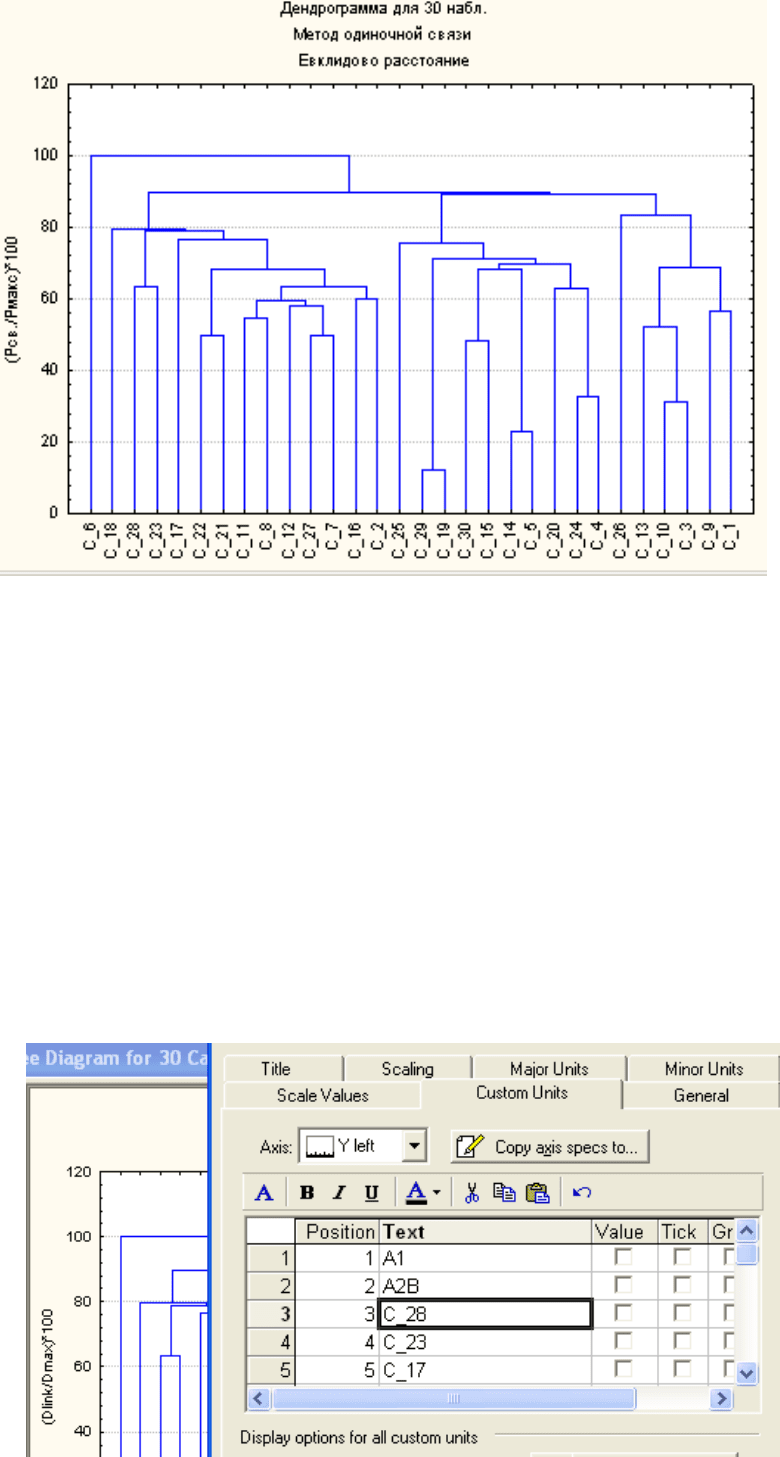
На графике по оси абсцисс отложены объекты (наблюдения). В данном

случае – это 30 горизонтов, соответствующие 5 разрезам дерново- подзоли-

стой почвы. По оси ординат отложено Евклидово расстояние между объекта-

ми и группами объектов, рассчитанное по свойствам объектов (наблюдений).

В группы объединяются объекты (и/или их группы), находящиеся на самом

близком расстоянии.

Дважды щелкнув по графику можно перейти в режим оформления, где

можно заменить номера объектов (наблюдений) на их имена. Для этого в поя-

вившемся меню выберите вкладку Единицы, заданные пользователем (Cus-

tom Units). Для сохранения имени горизонта в строке используйте клавишу

Enter. Замените порядковые номера наблюдений названиями горизонтов. На-

жмите OK. Сохраните график в файле результатов Excel.

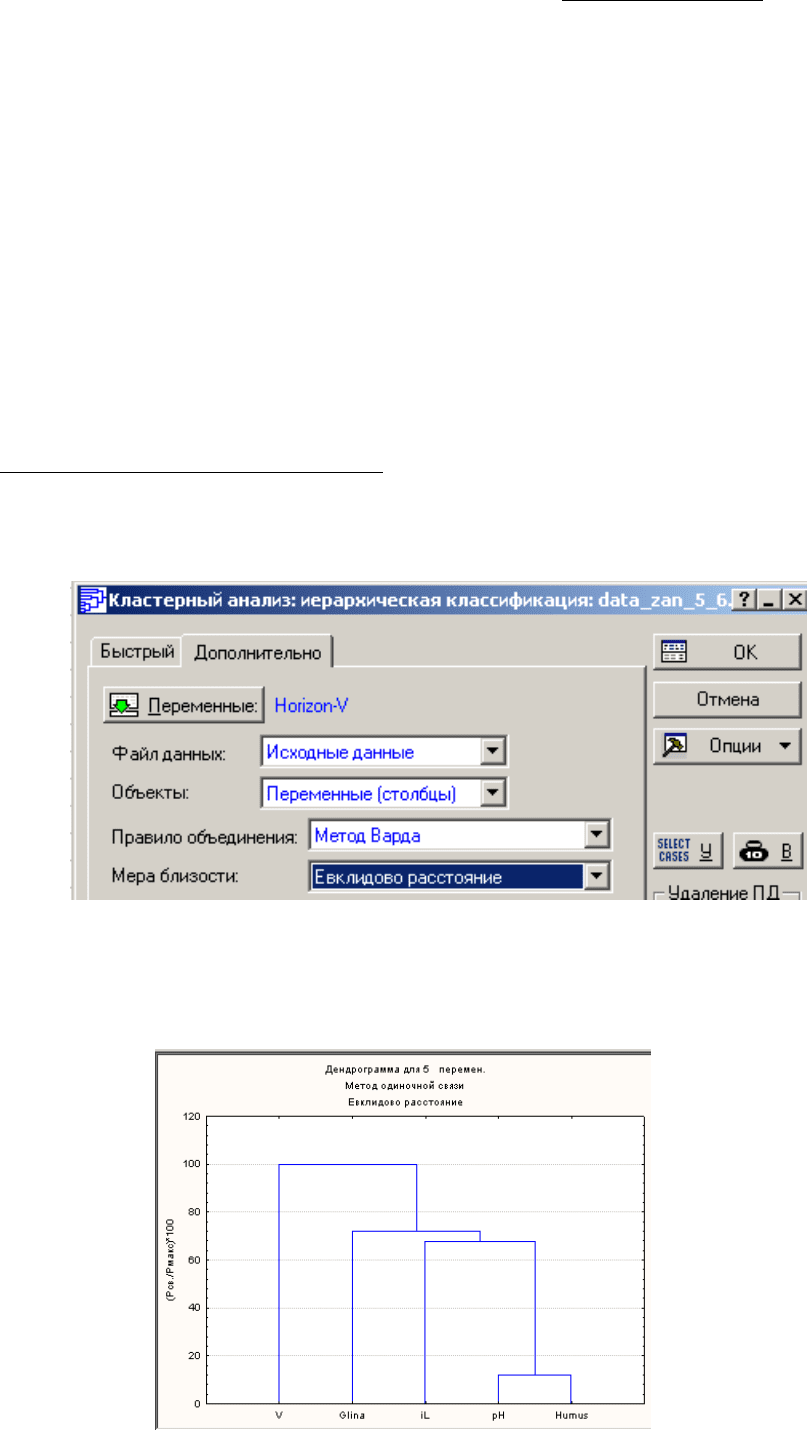
Проведите иерархический кластерный анализ методом Варда с исполь-

зованием Евклидового расстояния. Этот метод отличается от всех других ме-

тодов, поскольку он использует методы дисперсионного анализа для оценки

расстояний между кластерами. Метод Варда минимизирует сумму квадратов

для любых двух кластеров, которые могут быть сформированы на каждом ша-

ге. При использовании данного метода получаются кластеры малого размера.

Результаты сохраните в файле Excel.

На этой же панели меню, где строятся дендрограммы (см. стр. 47), мож-

но сохранить в виде таблицы порядок объединения объектов - схема объеди-

нения (Amalgamation schedule), график схемы объединения (Graph of Amal-

gamation schedule), матрицу расстояний между объектами (Distance matrix),

а также среднее и стандартное отклонение для полученных классов – Описа-

тельные статистики (Descriptive statistics).

СРАВНЕНИЕ ПЕРЕМЕННЫХ. Кластерный анализ позволяет также

оценивать близость переменных между собой. Для этого на первой панели в

поле Объекты (Cluster) выберите Variables (Columns)..

Для 5 переменных проведите иерархический кластерный анализ мето-

дом одиночной связи и методом Варда с использованием Евклидового рас-

стояния. Графики (2 шт.) сохраните в файле Excel.

МЕТОД K-СРЕДНИХ. Вернитесь в самое начало анализа и выберите

Кластеризацию методом к-средних (K-means clustering).

По методу K средних будет построено K кластеров, расположенных на воз-

можно больших расстояниях друг от друга. Расчеты начинаются K кластеров,

в которые объекты объединены случайным образом. Процедура состоит в из-

менении принадлежности объектов к кластерам так, чтобы: изменчивость

внутри кластеров сделать минимальной, изменчивость между кластерами -

максимальной. Эта оценка производиться с помощью дисперсионного анали-

за. Выберите закладку Дополнительно (Advanced).

Необходимо произвести выбор переменных (Variables), по которым бу-

дет проводиться анализ (C, PHS, IL, G, V) и выбор типа анализа (для объектов

или для самих переменных) в окошке Объекты (Cluster), - точно такой, как и

при иерархической классификации.

Укажите переменные: C, PHS, IL, G, V, и выберите анализ объектов-

наблюдений (Cases (row)). Затем нужно задать Число кластеров (Number of

clusters) и число итераций для расчетов (Number of iterations). Кроме этого,

можно разным способом задать Начальные центры кластеров (Initial clus-

ter centers).

Для ваших данных проведите кластеризацию методом k-средних,

задав

3 кластера. Число итераций возьмите по умолчанию, равное 10. Начальные

центры классов задайте через одинаковые интервалы в ранжированном ряду

расстояний Сортировать расстояния и выбрать наблюдения на постоян-

ных интервалах (Sort distances and take observations at constant intervals).

Нажмите ОК.