Мешалкина Ю.Л., Самсонова В.П. Математическая статистика в почвоведении: Практикум

Подождите немного. Документ загружается.

Занятие 4. Регрессионный анализ

ЦЕЛЬ занятия - провести множественный линейный регрессионный

анализ данных зависимости урожайности от почвенных признаков; опреде-

лить переменные, влияющие на урожайность; оценить степень влияния каж-

дой из переменных; исследовать качество аппроксимации зависимости.

Войдите в пакет STATISTICA (см. занятие №1). В программе

STATISTICA создайте новый файл данных для своего варианта (см. занятие

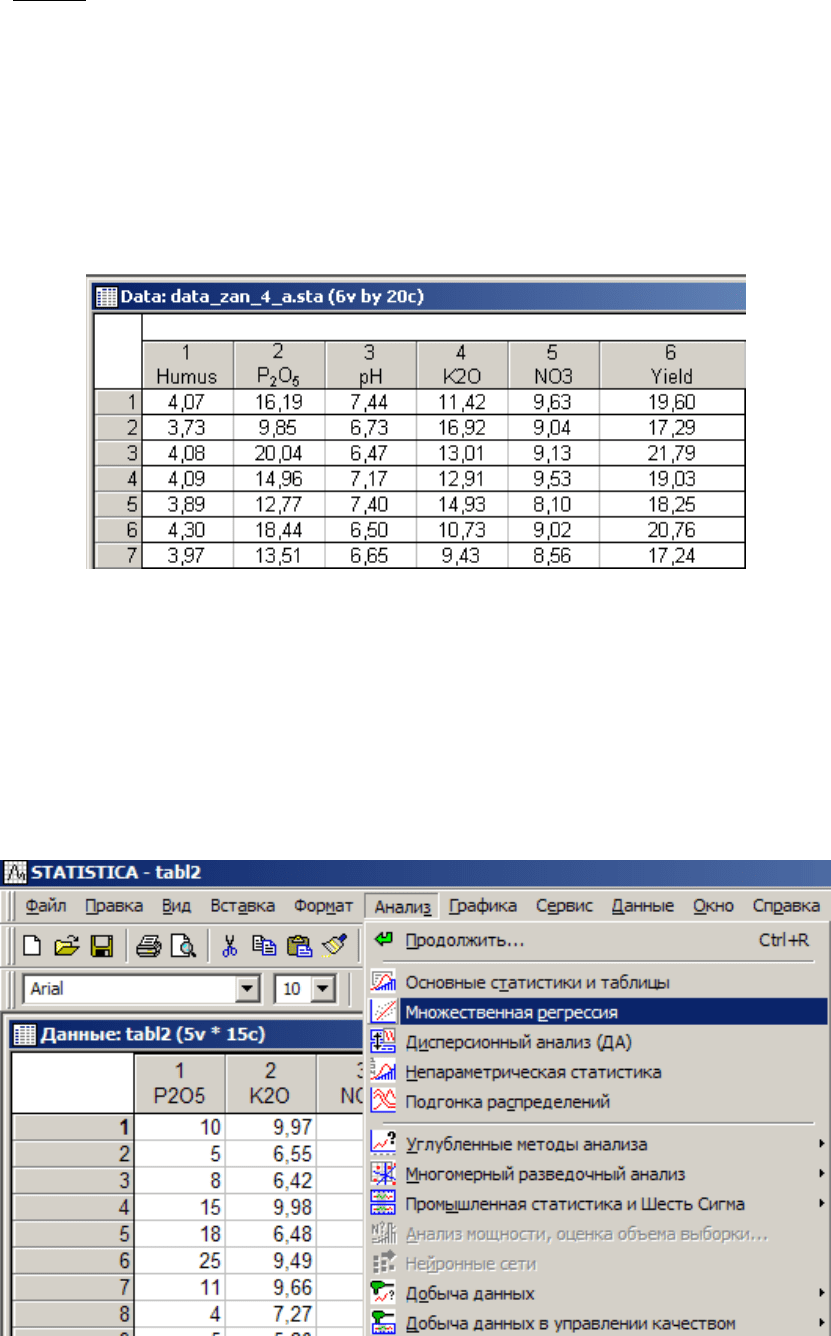
№3). Введите данные как показано на картинке ниже. Признаки – это столб-

цы, строки – это наблюдения.

Каждому наблюдению (точке на поле), соответствует урожай сельско-

хозяйственной культуры, указанный в пересчете на ц/га, (здесь переменная

Yield) и почвенные свойства, измеренные в почвенном образце, в данном слу-

чае – это содержание гумуса, рН , содержание подвижного фосфора, калия и

нитратов.

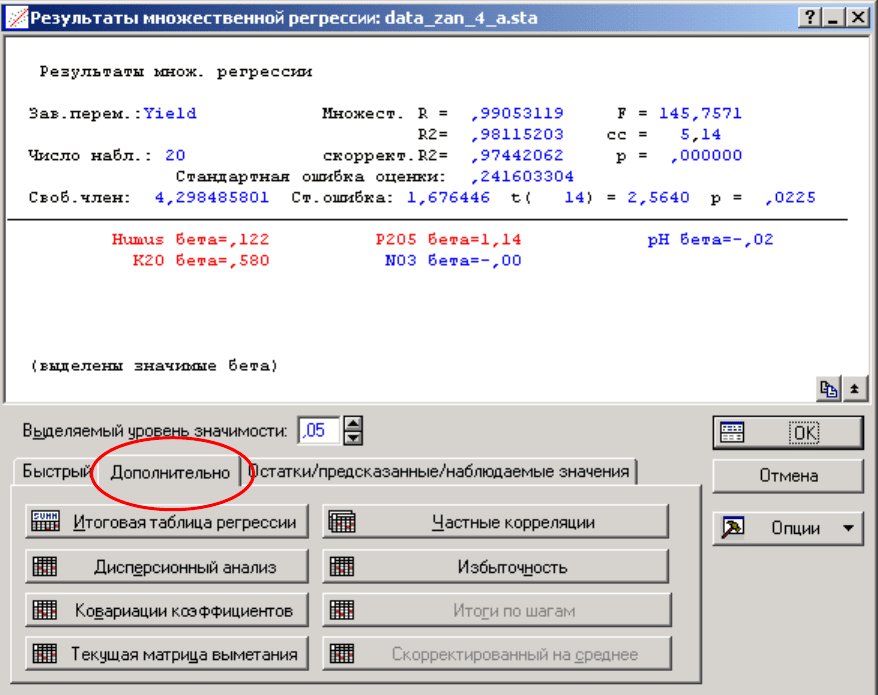
Щелкнув на кнопке Анализ (Statistics) откройте меню и затем выбери-

те раздел Множественная регрессия (Multiple Regression).

Назначение множественной регрессии состоит в анализе связи между

несколькими независимыми переменными (называемыми также регрессорами

или предикторами) – в данном случае, почвенными свойствами и зависимой

переменной – урожаем.

Выберите закладку Дополнительно (Advanced).

Щелкните по кнопке Переменные (Variables), задайте зависимые и не-

зависимые переменные. В нашем случае зависимой переменной (Dependent)

будет урожай сельскохозяйственной культуры (Yield), независимые перемен-

ные (Independent)- почвенные свойства (например, P

, hum, pH, K

O, NO

Обратите внимание, что вообще Файл данных (Input file) может содержать

данные как в исходном виде, так и в виде корреляционной матрицы. Нажмите

ОК, запустив тем самым анализ.

В результате работы программы появляется новая панель с расчетными

характеристиками (см. стр. 33). На появившейся панели отображается множе-

ственный коэффициент корреляции (R), его квадрат (коэффициент детерми-

нации), “скорректированный” коэффициент детерминации. Коэффициент

множественной корреляции R определяет степень тесноты связи результи-

рующего признака Y со всем набором независимых признаков X

,...,X

. В слу-

чае парной регрессии (т.е. при наличии всего одного признака X

) R совпадает

с коэффициентом корреляции Пирсона. По значению R-квадрат можно опре-

делить, насколько хорошо модель описывает данные, так как значение R рав-

но отношению дисперсии признака Y, объясненной регрессионной моделью,

к общей дисперсии признака Y. Значение R-квадрат близкое к 1,0 показывает,

что с помощью модели объясняется почти вся изменчивость Y.

На панели также приведены результаты дисперсионного анализа для

проверки гипотезы об адекватности модели: величина F-критерия, соответст-

вующее число степеней свободы для уравнения и уровень значимости (р),

стандартная ошибка оценки (Standart error estimate), оценка свободного чле-

на (intercept) и значение t-критерия для него с соответствующим уровнем

значимости (р). Значимые (отличные от нуля) оценки высвечиваются крас-

ным цветом.

Для каждого признака приведены стандартизованные коэффициенты

регрессии (см. далее), обозначенные бета (beta). Красным цветом обозначены

значимые коэффициенты.

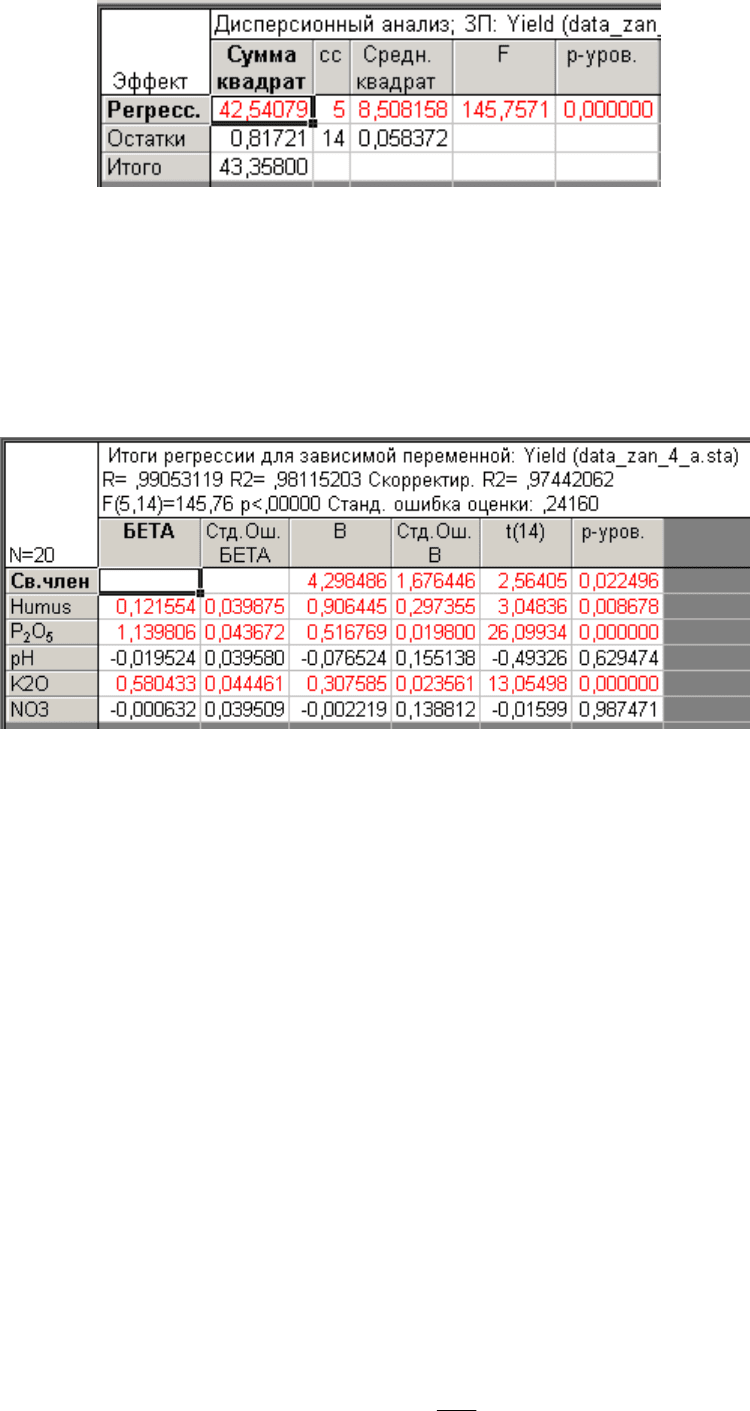
Результаты расчетов можно вывести в виде таблиц. На вкладке Допол-

нительно (Advanced) нажмите кнопку Дисперсионный анализ (ANOVA-

overall goodness of fit).

В появившейся таблице дисперсионного анализа уравнение регрессии

выступает в качестве влияющего фактора. Скопируйте таблицу в отчет в про-

грамме Excel.

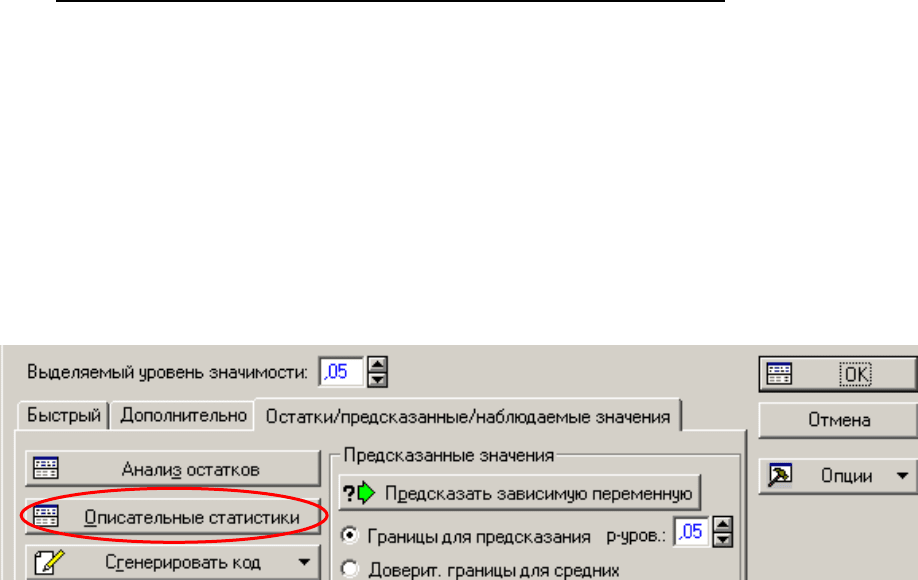
Для продолжения анализа в нижнем левом углу нажмите на свернутую

панель Множественная регрессия (Multiple Regression). На вкладке Допол-

нительно (Advanced) нажмите кнопку Итоговая таблица регрессии (Sum-

mary: regression results). Появится таблица, где суммированы результаты

регрессионного анализа для каждой из независимых переменных. Скопируйте

шапку и таблицу в отчет. Оцените отличие обычного и скорректированного

коэффициентов детерминации.

Аппроксимирующая модель подбирается в виде:

Y=const+B

+ …+ B

где В

, В

2 …

служат оценками генеральных параметров β

, β

…β

. Величина

показывает, насколько в среднем изменяется урожай (признак Y) при уве-

личении соответствующего независимого признака X

на единицу (шкалы его

измерения) при фиксированных значениях других признаков, входящих в

уравнение регрессии. Эти коэффициенты – величины размерные. В таблице

для каждого коэффициента B приведены их стандартные ошибки (Std. Err. of

B), а также значения критерия Стьюдента (в скобках указано число степеней

свободы) и уровень значимости (обозначен как p-уровень) для проверки гипо-

тезы о равенстве коэффициентов нулю. Проверьте по скопированной таблице,

какие из коэффициентов равны нулю, а какие отличны от нуля.

Исходя из этих данных, можно рассчитать доверительные интервалы

для коэффициентов регрессии.

kitSB

Bii

,...2,1,* =±

Термином БЕТА (Beta) в таблице названы стандартизованные коэффи-

циенты, связанные с обычными коэффициентами через соотношение:

BetaB

Как видно из уравнения коэффициенты бета - это безразмерные величи-

ны. По их значениям можно сравнивать вклады независимых переменных в

урожай. Например, из таблицы видно, что наибольший вклад в урожай вносит

фосфор, следующий по значению признак – гумус и т.п. Для значения рН уро-

вень значимости для проверки гипотезы о равенстве коэффициента нулю

больше значения 0,05, и, следовательно, нулевая гипотеза принимается. Ко-

эффициент для значения рН неотличим от нуля. Вклад нитратов в данном

случае практически тоже равен нулю.

Проверьте по скопированной таблице, какие из коэффициентов отличны

от нуля. Выпишите окончательное уравнение регрессии. Например, в данном

случае:

Yield [ц/га] = 4,29 [ц/га] + 0,91[ц/(га*%)] *Humus [%] + 0, 52 [(ц/га)/ мг-

экв. / 100 г. почвы] * P

[мг-экв. / 100 г. почвы] + 0,31 [(ц/га)/ мг-экв. / 100 г.

почвы] *K

O[мг-экв. / 100 г. почвы].

Рассчитайте 95% доверительные интервалы для коэффициентов полу-

ченного уравнения. Например, для 90% -доверительного интервала и числа

степеней свободы, равного 16 (число наблюдений 20 минус число переменных

4), значение двухстороннего t- критерия будет равно 1,75. Коэффициент рег-

рессии для гумуса будет с вероятностью 90% изменяться в следующих преде-

лах: от 0,38 (0,91 – 0,30*1,75) до 1,44 (0,91 + 0,30*1,75), где точечная оценка

коэффициента регрессии и его ошибки равны соответственно 0,91 и 0,30.

АНАЛИЗ НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ. Под термином

мультиколлинеарность понимают наличие взаимосвязей между так называе-

мыми независимыми признаками, по которым строиться регрессионное урав-

нение. При ее наличии снижается точность оценок регрессионных коэффици-

ентов. Кроме того добавление небольшого числа наблюдений может привести

к сильным сдвигам в значениях регрессионных коэффициентов.

Для продолжения работы перейдите на вкладку Остатки/ предсказан-

ные/ наблюдаемые значения (Residuals/assumptions/ prediction). Для по-

строения коэффициентов корреляции нажмите на кнопку Описательные

статистики (Descriptive Statistics).

На появившейся панели перейдите на вкладку Дополнительно (Ad-

vanced) и выберите кнопку Корреляции (Correlations) для построения кор-

реляционной таблицы между признаками. При построении таблицы корреля-

ций выберите все признаки. Скопируйте таблицу в отчет. При анализе ре-

зультатов нужно учесть, что при числе степеней свободы ν=19 значимыми (то

есть отличными от нуля) можно считать коэффициенты, превышающие по

модулю 0,45. А при ν=14 – 0,53. Если независимые переменные окажутся тес-

но связанными между собой (коэффициенты корреляции по модулю равны

или более 0,85), то следует исключить коррелированные признаки, оставив

один из них. Затем можно использовать алгоритмы пошаговой регрессии.

Humus

K2O

Yield

Другой вариантом при наличии большего числа коррелированных при-

знаков является проведение факторного анализа (метод главных компонент) и

переход к новому набору переменных, которые будут не связаны между со-

бой. Множественная регрессия строиться для этих новых переменных (ком-

понент).

Для построения попарных графиков между переменными выберите

кнопку Матричный график (Matrix plot of correlations). Сначала выберите

все переменные и урожай. Рассмотрите график. Затем постройте график толь-

ко для значимых переменных и для урожая. Для выделения нужных перемен-

ных используйте клавишу Ctrl. Скопируйте график в отчет.

АНАЛИЗ ОСТАТКОВ. Отклонение отдельной точки от линии регрес-

сии (от предсказанного значения) называется остатком. Анализ остатков -

важная составляющая регрессионного анализа, позволяющая проверить, на-

сколько хорошо выполняются основные предположения множественной рег-

рессии. Наличие выбросов (т.е. экстремальных наблюдений) может вызвать

смещение оценок, "сдвинуть" линию регрессии и тем самым, вызывать сме-

щение регрессионных коэффициентов. Часто исключение лишь одного экс-

тремального наблюдения приводит к изменению результата.

Для того чтобы выполнить анализ остатков, в нижнем левом углу на-

жмите на свернутую панель Множественная регрессия (Multiple

Regression). Появится размещенная выше таблица Просмотра описатель-

ных статистик (Review Descriptive Statistics). Чтобы подняться в меню на

более высокий уровень, нажмите кнопку Отмена (Cancel).

Появится следующее меню. Выберите закладку Остатки/ предсказан-

ные/ наблюдаемые значения (Residuals/assumptions/ prediction).

Нажмите кнопку Анализ остатков (Perform residual analysis). Появит-

ся меню:

Выберите закладку Остатки (Residuals) и нажмите кнопку Гистограм-

ма остатков (Histogram of residuals). В множественной регрессии предпола-

гается, что остатки распределены нормально. Оцените, насколько это допу-

щение выполняется в Вашем случае. Появившийся график скопируйте в от-

чет.

Вернитесь к меню.

Выберите закладку Диаграмма рассеяния (Scatterplots).

Для построения графика зависимости наблюдаемых значений урожая от

предсказанных значений урожая используйте клавишу Предсказанные и на-

блюдаемые (Predicted vs. Observed). Скопируйте этот график в отчет. Чем

лучше модель оценивает данные урожайности, тем ближе точки располагают-

ся к прямой.

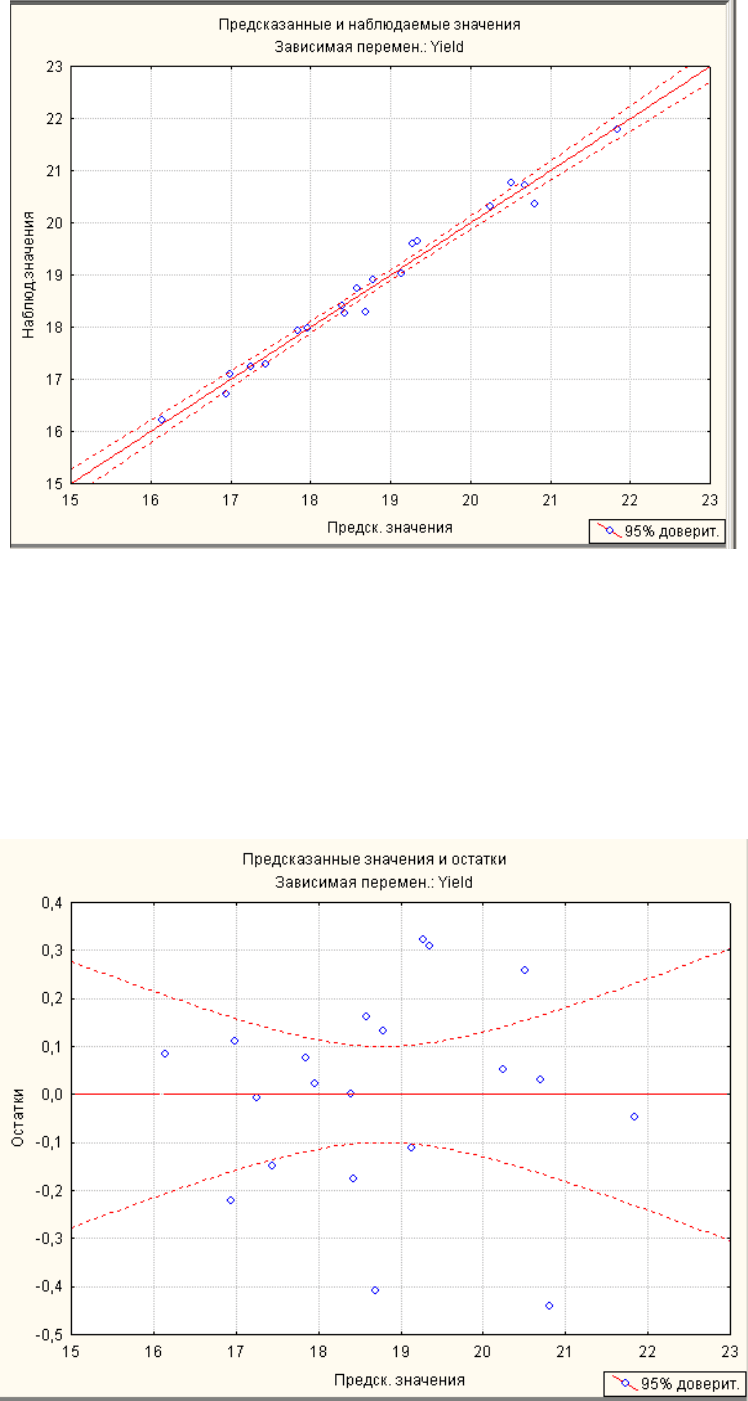
Для построения графика зависимости остатков от предсказанных значе-

ний используйте клавишу Предсказанные и остатки (Predicted vs. re-

siduals). Скопируйте график в отчет. Чем меньше разброс значений вдоль ли-

нии, тем, очевидно, лучше прогноз. В случае хорошей аппроксимации остатки

не должны зависеть от наблюдаемых и предсказанных величин.

Для построения нормального вероятностного графика остатков выбери-

те закладку Вероятностные графики (Probability plots) и нажмите клавишу

Нормальный (Normal plot of residuals). Скопируйте график в отчет. В случае

хорошей аппроксимации остатки должны иметь нормальное распределение.

ПОШАГОВАЯ РЕГРЕССИЯ. Существует две схемы пошаговой регрес-

сии: «с исключением» признаков и «с включением».

Первый алгоритм состоит в том, что после построения уравнения рег-

рессии и оценки значимости всех коэффициентов из модели исключают тот

признак, коэффициент при котором незначим и имеет наименьшее значение t .

После этого получают новое уравнение множественной регрессии и снова

производят оценку значимости всех оставшихся коэффициентов регрессии.

Если среди них опять окажутся незначимые, то опять исключают признак с

наименьшим значением t -критерия. Процесс исключения признаков останав-

ливается на том шаге, при котором все регрессионные коэффициенты значи-

мы. При использовании этой схемы негативные последствия мультиколлине-

арности могут сказаться.

При реализации второго алгоритма первым в уравнение включается

признак, наиболее тесно коррелирующий с Y, вторым в уравнение включается

тот признак, который в паре с первым из отобранных дает максимальное зна-

чение множественного коэффициента корреляции, и т.д. На каждом шаге по-

лучают новое значение множественного коэффициента корреляции (большее,

чем на предыдущем шаге); тем самым определяется вклад каждого отобран-

ного признака в объясненную дисперсию Y.

Нажмите в нижнем левом углу на свернутую панель Множественная

регрессия (Multiple Regression). Чтобы вернуться назад, несколько раз на-

жимайте Отмена (Cancel) до тех пор, пока не появится следующее меню: