Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.

240
хичесих систем мо т использоваться все три понятия; слчаи, о -
да применяется тольо одно, являются ислючением.
Страты. Уровни описания, или абстраирования. Напомним, что
основная дилемма при описании систем состоит в том, что прихо-
дится находить омпромисс межд простотой описания и необхо-
димостью чета мно очисленных фаторов и харатеристи слож-
ной системы. Разрешение этой дилеммы ищется в иерархичесом
описании. Система задается семейством моделей, аждая из ото-
рых описывает поведение системы с точи зрения различных ров-
ней абстра ирования. Для аждо о ровня иерархии сществет ряд
харатерных особенностей и переменных, заонов и принципов, с
помощью оторых описывается поведение системы. Чтобы таое
иерархичесое описание было эффетивным, необходима а
можно большая независимость моделей для различных ровней
системы. Таим образом, процесс расчленения системы на ровни,
харатеризющие техноло ичесие, информационные и эономи-
чесие аспеты ее фнционирования, называется стратифициро-
ванием системы, а сами ровни — стратами. На аждой страте в
иерархии стртр имеется свой собственный набор переменных,
оторые позволяют в значительной степени о раничить изчение
тольо одной стратой. Независимость страт отрывает возмож-
ность для более лбоо о и детально о изчения системы, однао
предположение о независимости страт может привести неполно-
м пониманию поведения системы в целом. Приведем несольо
примеров систем, требющих стратифицированно о описания.
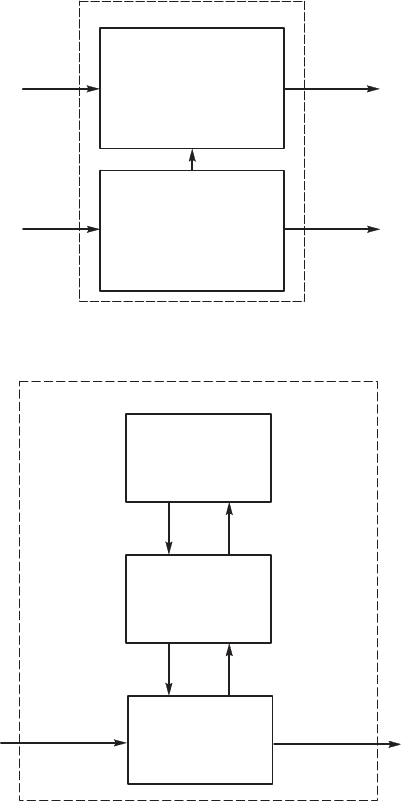
1. Модель ЭВМ. Фнционирование ЭВМ обычно описывает-
ся не менее чем на двх стратах (рис. 7.8).
На первой страте система описывается на язые физичесих
заонов, правляющих работой и взаимодействием ее составных
частей, в то время а на второй страте имеют дело с абстратными
нефизичесими понятиями: таими, а двоичные разряды, фай-
лы, информационные потои и т. д. На страте физичесих заонов
представляет интерес правильное фнционирование различных
элетронных омпонентов, а на страте обработи информации —
проблемы вычисления, про раммирования и т. п.
2. Автоматизированный промышленный омплес. Этот омплес
обычно моделирют на трех стратах: 1) физичесие процессы обра-
боти материалов и преобразования энер ии; 2) правление в обра-
бота информации; 3) эономиа производства с точи зрения е о
производительности и прибыльности (рис. 7.9). Заметим, что на лю-
бой из этих трех страт мы имеем дело с одним предметом — основ-
ным физичесим продтом. На первой страте он рассматривается
а физичесий объет, оторый подлежит обработе в соответс-
241
твии с физичесими заонами, на второй страте е о рассматривают
а правляемю переменню; на третьей страте это же товар а
эономичесая ате ория. Для аждо о из этих аспетов системы
имеется свое описание, однао система остается одной и той же.
3. Стртра системы правления народным хозяйством страны.
Система правления народным хозяйством страны может быть
Îáðàòíàÿ ñâÿçüÂìåøàòåëüñòâî
Îáðàòíàÿ ñâÿçüÓïðàâëåíèå
Ñòðàòà 1:
Ôèçè÷åñêèå
ïðîöåññû
Ñòðàòà 2:
Îáðàáîòêà
èíôîðìàöèè
è óïðàâëåíèå
Ñòðàòà 3:
Ýêîíîìè÷åñêèå
ôàêòîðû
Ïðåäïðèÿòèå
Ñûðüå ïðîäóêöèÿ
Ãîòîâàÿ
Ñòðàòà 1:
Ôèçè÷åñêèå
îïåðàöèè
Ñòðàòà 2:
Ìàòåìàòè÷åñêèå
îïåðàöèè
(ïðîãðàììèðîâàíèå
è ðåàëèçàöèÿ
ïðîãðàììû)
Âõîä
ÝÂÌ
Âûõîä
Âõîä
Âûõîä
Рис. 7.9. Стратифицированное представление
автоматизированноо машинноо производства
Рис. 7.8. Стратифицированное представление ЭВМ
242
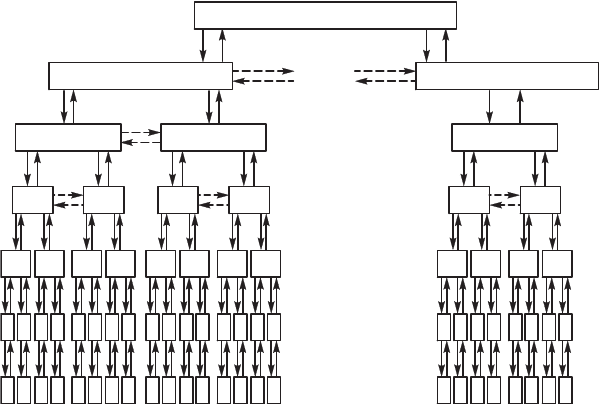
представлена в виде семи страт (рис. 7.10). Первые три нижние стра-
ты относятся проблематие, связанной с решением задач автома-
тичесо о или автоматизированно о правления производством. На
этих ровнях большю роль в процессе правления и рают автома-
тичесие средства, а не челове. На остальных (верхних) ровнях
осществляется административное и ор анизационное (планирова-
ние эономии) правление, и большее значение в процессе это о
правления принадлежит людям, а не автоматичесим стройствам.
Примеров стратифицированно о описания систем можно
привести очень мно о. Однао и приведенных примеров доста-
точно, чтобы сформлировать общие свойства стратифицирован-
но о описания систем:
1. Выбор страт, в терминах оторых описывается данная сис-
тема, зависит от наблюдателя, е о знания и заинтересованности
в деятельности системы, хотя для мно их систем неоторые стра-
ты ажтся естественными, внтренне им присщими.
2. Аспеты описания фнционирования системы на различ-
ных стратах в общем слчае не связаны межд собой. Поэтом
. . .
. . .
. . .
4
3
2 2
6
1 1
3
2 2
1 1
4
3
2 2
5
1 1
3
2 2
1 1
4
3
2 2
1 1
3
2 2
1 1
4
3
2 2
5
1 1
3
2 2
1 1
6
7
4
3
2 2
1 1
3
2 2
1 1
4
3
2 2
5
1 1
3
2 2
1 1
Рис. 7.10. Стратифицированное представление системы правления народ-
ным хозяйством страны (по В.А. Трапезниов):
1 — страта 1: автоматичесие реляторы ареатов; 2 — страта 2:
системы правления ареатами; 3 — страта 3: СУ автоматичесими
линиями; 4 — страта 4: цеховые СУ; 5 — страта 5: СУ предприятиями;
6 — страта 6: СУ отраслями народноо хозяйства; 7 — страта 7:
СУ народным хозяйством
243
принципы и заоны, использемые для харатеристии системы
на любой страте, в общем слчае не мо т быть выведены из при-
нципов, использемых на др их стратах.
3. Сществет асимметричная зависимость межд словиями
фнционирования системы на различных стратах.
4. На аждой страте имеется свой собственный набор терми-
нов, онцепций и принципов.
5. Понимание системы возрастает при последовательном пере-
ходе от одной страты др ой: чем ниже спсаемся по иерархии,
тем более детальным становится расрытие системы; чем выше под-
нимаемся, тем яснее становится смысл и значение всей системы.
Слои. Уровни сложности принимаемоо решения. Почти в любой
реальной ситации принятия решения сществют две предельно
простые, но чрезвычайно важные особенности:
1) о да приходит время принимать решения, принятие и вы-
полнение решения нельзя отладывать;
2) неясность относительно последствий различных альтернатив-
ных действий и отстствие достаточных знаний об имеющихся свя-
зях препятствют .достаточно полном формализованном описа-
нию ситации, необходимом для рационально о выбора действий.
Эти два фатора приводят основной дилемме принятия ре-
шения: с одной стороны, необходимо действовать немедленно,
с др ой же — столь же необходимо, прежде чем пристпить дейс-
твиям, попытаться лчше понять ситацию. При принятии решения
в сложных ситациях решение этой дилеммы ищт в иерархичесом
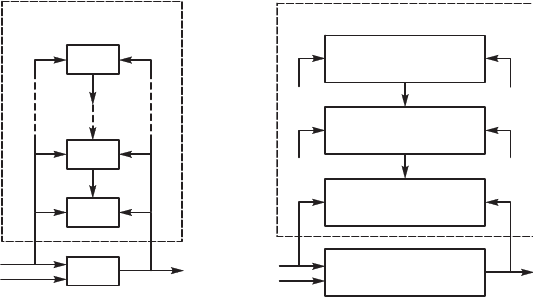
подходе (рис. 7.11). Сложная проблема принятия решения разби-
вается на семейство последовательно расположенных более простых
подпроблем D
i
, i = , та что решение всех подпроблем позволяет
решить и исходню проблем Р. Таая иерархия называется иерар-
хией слоев принятия решений, а вся система (D на рис. 7.11) — мно-
ослойной системой (принятия решений).
Важным видом иерархий является фнциональная иерархия
принятия решений или правления. Эта иерархия возниает в связи
с тремя основными аспетами проблемы принятия решения в сло-
виях полной неопределенности (рис. 7.12). Фнциональная иерар-
хия, изображенная на рис. 7.12, состоит из трех слоев:
1. Слой выбора: задача это о слоя — выбор способа действий.
2. Слой общения, или адаптации: задача слоя — онретизация
множества неопределенностей, с оторым имеет дело слой выбора.
3. Слой самоор анизации: задача слоя — выбор стртры,
фнции и страте ии, оторые использются на нижележащих
слоях, таим образом, чтобы по возможности приблизиться
лобальной цели.
1 n,

242
представлена в виде семи страт (рис. 7.10). Первые три нижние стра-
ты относятся проблематие, связанной с решением задач автома-
тичесо о или автоматизированно о правления производством. На
этих ровнях большю роль в процессе правления и рают автома-
тичесие средства, а не челове. На остальных (верхних) ровнях
осществляется административное и ор анизационное (планирова-
ние эономии) правление, и большее значение в процессе это о
правления принадлежит людям, а не автоматичесим стройствам.
Примеров стратифицированно о описания систем можно
привести очень мно о. Однао и приведенных примеров доста-
точно, чтобы сформлировать общие свойства стратифицирован-
но о описания систем:
1. Выбор страт, в терминах оторых описывается данная сис-
тема, зависит от наблюдателя, е о знания и заинтересованности
в деятельности системы, хотя для мно их систем неоторые стра-
ты ажтся естественными, внтренне им присщими.
2. Аспеты описания фнционирования системы на различ-
ных стратах в общем слчае не связаны межд собой. Поэтом
. . .
. . .
. . .
4
3
2 2
6
1 1
3
2 2
1 1
4
3
2 2
5
1 1
3
2 2
1 1
4
3
2 2
1 1
3
2 2
1 1
4
3
2 2
5
1 1
3
2 2
1 1
6
7
4
3
2 2
1 1
3
2 2
1 1
4
3
2 2
5
1 1
3
2 2
1 1
Рис. 7.10. Стратифицированное представление системы правления народ-
ным хозяйством страны (по В.А. Трапезниов):
1 — страта 1: автоматичесие реляторы ареатов; 2 — страта 2:
системы правления ареатами; 3 — страта 3: СУ автоматичесими
линиями; 4 — страта 4: цеховые СУ; 5 — страта 5: СУ предприятиями;
6 — страта 6: СУ отраслями народноо хозяйства; 7 — страта 7:
СУ народным хозяйством
243
принципы и заоны, использемые для харатеристии системы
на любой страте, в общем слчае не мо т быть выведены из при-
нципов, использемых на др их стратах.
3. Сществет асимметричная зависимость межд словиями
фнционирования системы на различных стратах.
4. На аждой страте имеется свой собственный набор терми-
нов, онцепций и принципов.
5. Понимание системы возрастает при последовательном пере-
ходе от одной страты др ой: чем ниже спсаемся по иерархии,
тем более детальным становится расрытие системы; чем выше под-
нимаемся, тем яснее становится смысл и значение всей системы.
Слои. Уровни сложности принимаемоо решения. Почти в любой
реальной ситации принятия решения сществют две предельно
простые, но чрезвычайно важные особенности:
1) о да приходит время принимать решения, принятие и вы-
полнение решения нельзя отладывать;
2) неясность относительно последствий различных альтернатив-
ных действий и отстствие достаточных знаний об имеющихся свя-
зях препятствют .достаточно полном формализованном описа-
нию ситации, необходимом для рационально о выбора действий.
Эти два фатора приводят основной дилемме принятия ре-
шения: с одной стороны, необходимо действовать немедленно,
с др ой же — столь же необходимо, прежде чем пристпить дейс-
твиям, попытаться лчше понять ситацию. При принятии решения
в сложных ситациях решение этой дилеммы ищт в иерархичесом
подходе (рис. 7.11). Сложная проблема принятия решения разби-
вается на семейство последовательно расположенных более простых
подпроблем D
i
, i = , та что решение всех подпроблем позволяет
решить и исходню проблем Р. Таая иерархия называется иерар-
хией слоев принятия решений, а вся система (D на рис. 7.11) — мно-
ослойной системой (принятия решений).
Важным видом иерархий является фнциональная иерархия
принятия решений или правления. Эта иерархия возниает в связи
с тремя основными аспетами проблемы принятия решения в сло-
виях полной неопределенности (рис. 7.12). Фнциональная иерар-
хия, изображенная на рис. 7.12, состоит из трех слоев:
1. Слой выбора: задача это о слоя — выбор способа действий.
2. Слой общения, или адаптации: задача слоя — онретизация
множества неопределенностей, с оторым имеет дело слой выбора.
3. Слой самоор анизации: задача слоя — выбор стртры,
фнции и страте ии, оторые использются на нижележащих
слоях, таим образом, чтобы по возможности приблизиться
лобальной цели.
1 n,
244
Мнооэшелонные системы: оранизационные иерархии. Это по-
нятие иерархии подразмевает, что: 1) система состоит из семейс-
тва чето выделенных взаимодействющих подсистем; 2) неото-
рые из подсистем являются принимающими решения элементами
и 3) принимающие решения элементы распола аются иерархи-
чеси в том смысле, что неоторые из них находятся под влияни-
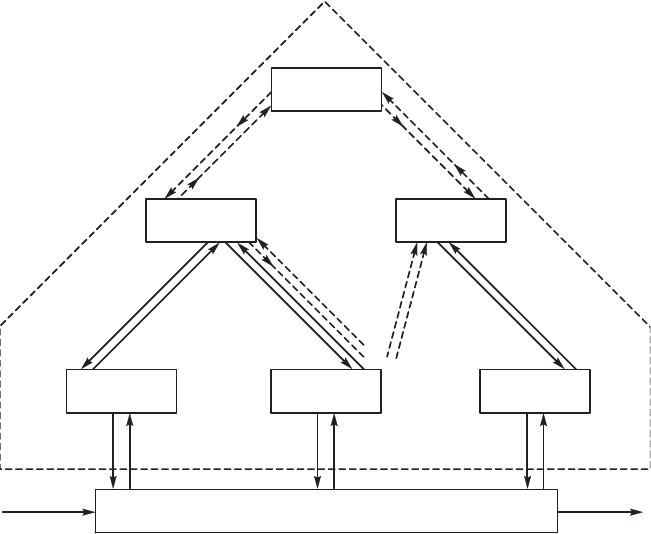
ем или правляются др ими решающими элементами. Бло-схе-
ма тао о типа приведена на рис. 7.13. Уровень в таой системе
называется эшелоном. Таие системы называются мно оэшелон-
ными, мно оровневыми или мно оцелевыми.
Для эффетивно о использования мно оровневой стртры
сщественно, чтобы элементам принятия решения была предо-
ставлена неоторая свобода действий. Должно быть проведено
рациональное распределение силий по принятию решений меж-
д элементами различных ровней. Тольо при этом словии б-
дет оправдано само сществование иерархии. По харатер ие-
рархичесо о расположения образющих систем элементов раз-
личают следющие системы принятия решений:
— одноровневые одноцелевые системы;
— одноровневые мно оцелевые системы;
— мно оровневые мно оцелевые системы.
Отметим еще несольо свойств, харатерных для любых ие-
рархичесих стртр:
1) элемент верхне о ровня иерархии имеет дело с более
рпными подсистемами или с более широими аспетами пове-
дения системы в целом;
ðåøåíèé D
Ñèñòåìà ïðèíÿòèÿ
D
n
X
1
D
1
P
X
2
D
2
X
n – 1
Ïðîöåññ
Îáó÷åíèå è
àäàïòàöèÿ
Èåðàðõèÿ ïðèíÿòèÿ ðåøåíèé
Ñàìîîðãàíèçàöèÿ
Âûáîð
Рис. 7.11. Мноослойная
иерархия системы
принятия решений
Рис. 7.12. Фнциональная
мноослойная иерархия
принятия решений
245
2) период принятия решения для элемента верхне о ровня
больше, чем для элементов нижних ровней;
3) элемент верхне о ровня имеет дело с более медленными
аспетами поведения всей системы;
4) описания и проблемы на верхних ровнях менее стрт-
рированы, содержат больше неопределенностей и более трдны
для формализации.
Преимщества иерархичесих систем правления (ИСУ). ИСУ
нашли широое распространение. Универсальный харатер ИСУ
обсловлен рядом преимществ, оторыми они обладают по
сравнению с др ими СУ, в частности с системами централизо-
ванно о правления:
1) свобода лоальных действий (в течение интервала време-
ни, обсловленных моментами постпления правляющих воз-
действий со стороны вышележаще о ровня);
2) возможность целесообразно сочетать различные для аж-
до о из ровней системы лоальные ритерии оптимальности и
лобальный ритерий оптимальности системы в целом;
. . .. . .
. . .
Èíôîðìàöèîííàÿ
îáðàòíàÿ
ñâÿçü
Óïðàâëåíèå
Îáðàòíàÿ
ñâÿçü
Ï ð î ö å ñ ñ
Ýøåëîí 3
Ýøåëîí 1
Ðåøàþùèé
ýëåìåíò
Èåðàðõèÿ ïðèíÿòèÿ ðåøåíèé
Êîîðäèíàöèÿ
Ýøåëîí 2
Рис. 7.13. Мнооровневая оранизация иерархий; мнооэшелонная система
244
Мнооэшелонные системы: оранизационные иерархии. Это по-
нятие иерархии подразмевает, что: 1) система состоит из семейс-
тва чето выделенных взаимодействющих подсистем; 2) неото-
рые из подсистем являются принимающими решения элементами
и 3) принимающие решения элементы распола аются иерархи-
чеси в том смысле, что неоторые из них находятся под влияни-
ем или правляются др ими решающими элементами. Бло-схе-
ма тао о типа приведена на рис. 7.13. Уровень в таой системе
называется эшелоном. Таие системы называются мно оэшелон-
ными, мно оровневыми или мно оцелевыми.
Для эффетивно о использования мно оровневой стртры
сщественно, чтобы элементам принятия решения была предо-
ставлена неоторая свобода действий. Должно быть проведено
рациональное распределение силий по принятию решений меж-
д элементами различных ровней. Тольо при этом словии б-
дет оправдано само сществование иерархии. По харатер ие-
рархичесо о расположения образющих систем элементов раз-
личают следющие системы принятия решений:
— одноровневые одноцелевые системы;
— одноровневые мно оцелевые системы;
— мно оровневые мно оцелевые системы.
Отметим еще несольо свойств, харатерных для любых ие-
рархичесих стртр:
1) элемент верхне о ровня иерархии имеет дело с более
рпными подсистемами или с более широими аспетами пове-
дения системы в целом;
ðåøåíèé D
Ñèñòåìà ïðèíÿòèÿ
D
n
X
1
D
1
P
X
2
D
2
X
n – 1
Ïðîöåññ
Îáó÷åíèå è
àäàïòàöèÿ
Èåðàðõèÿ ïðèíÿòèÿ ðåøåíèé
Ñàìîîðãàíèçàöèÿ
Âûáîð
Рис. 7.11. Мноослойная
иерархия системы
принятия решений
Рис. 7.12. Фнциональная
мноослойная иерархия
принятия решений
245
2) период принятия решения для элемента верхне о ровня
больше, чем для элементов нижних ровней;
3) элемент верхне о ровня имеет дело с более медленными
аспетами поведения всей системы;
4) описания и проблемы на верхних ровнях менее стрт-
рированы, содержат больше неопределенностей и более трдны
для формализации.
Преимщества иерархичесих систем правления (ИСУ). ИСУ
нашли широое распространение. Универсальный харатер ИСУ
обсловлен рядом преимществ, оторыми они обладают по
сравнению с др ими СУ, в частности с системами централизо-
ванно о правления:
1) свобода лоальных действий (в течение интервала време-
ни, обсловленных моментами постпления правляющих воз-
действий со стороны вышележаще о ровня);
2) возможность целесообразно сочетать различные для аж-
до о из ровней системы лоальные ритерии оптимальности и
лобальный ритерий оптимальности системы в целом;
. . .. . .
. . .
Èíôîðìàöèîííàÿ
îáðàòíàÿ
ñâÿçü
Óïðàâëåíèå
Îáðàòíàÿ
ñâÿçü
Ï ð î ö å ñ ñ
Ýøåëîí 3
Ýøåëîí 1
Ðåøàþùèé
ýëåìåíò
Èåðàðõèÿ ïðèíÿòèÿ ðåøåíèé
Êîîðäèíàöèÿ
Ýøåëîí 2
Рис. 7.13. Мнооровневая оранизация иерархий; мнооэшелонная система
246
3) отстствие необходимости пропсать очень большие по-
тои информации через один правляющий ор ан, та а при
использовании ИСУ информация с нижне о ровня передается
на верхний в обобщенном виде;
4) повышенная надежность СУ и большие возможности вве-
дения элементной избыточности в систем на необходимом ров-
не правления;
5) ибость и адаптивность СУ;
6) ниверсальность при решении однотипна в целом, но в де-
талях правления может отличаться;
7) в ряде слчаев — эономичесая целесообразность по срав-
нению с СУ иной стртры.
7.4. Формализация иерархичесих понятий
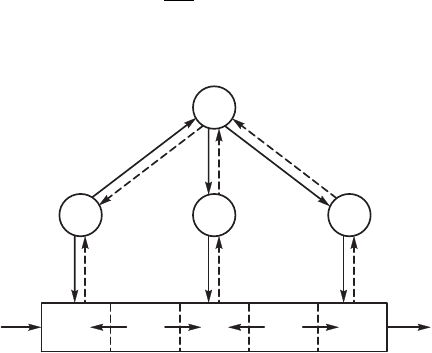
Координация. При оптимизации взаимодействия межд ров-
нями в ИСУ весьма важной является проблема оординации.
Псть система состоит из n подсистем перво о ровня S
1
, ..., S
n
,
правляющих процессов P и одной подсистемы второ о (высше-
о) ровня S
0
(рис. 7.14). Цель высшей подсистемы влиять на низ-
шие таим образом, чтобы дости алась общая цель, заданная для
всей системы. Это составляет содержание понятия оординации.
Схема, представленная на рис. 7.14, является простейшей, хотя
она обладает наиболее важными харатеристиами мно оровне-
вых ИСУ и может слжить в ачестве элементарно о блоа при
построении более сложных ИСУ. На рис. 7.14 приняты следю-
щие обозначения: u
i
, i = — правляющие воздействия на
подпроцесс P
i
; X — входные воздействия на процесс P ; β
i
— об-
β
1
ω
1
ω
i
ω
n
γ
i
β
i
β
n
α
1
α
i
α
i
α
n
γ
i
γ
n
S
i
U
i
P
i
S
1
P
1
U
1
S
n
U
n
Y
P
n
S
0
. . .. . .
X
Рис. 7.14. Двхровневая иерархичесая система правления
1 n,
247
ратная связь подсистем S
i
, с подпроцессом P
i
; γ
i
— оординир-
ющее воздействие на подсистем S
i
; ω
i
— обратная связь оорди-
натора S
0
с подсистемой S
i
; Y — выход процесса Р ; α
i
— связи
подпроцесса P
i
, с процессом Р, α = {α
1
, ..., α
n
}.
Та а подсистемы низше о ровня действют в направле-
нии достижения собственных лоальных целей, то межд ними
возниает онфлит, в резльтате оторо о лобальная цель сис-
темы может быть не дости нта. Поэтом задача оординатора
состоит в меньшении последствий тао о онфлита. Очевидно,
что онфлит не вознинет, если входы связей α
i
, желательные с
точи зрения аждой подсистемы S
i
, совпадают с теми, оторые
фатичеси имеют место в процессе работы системы. Следова-
тельно, лавный вопрос, оторый возниает в связи с задачей о-
ординации подсистем низше о ровня, состоит в том, аим об-
разом входы связей читываются этими подсистемами.
Возможны три способа анализа видов связей, аждом из о-
торых соответствет свой способ оординации: 1) подсистемы
низше о ровня решают свои лоальные задачи, предпола ая
входы связей равными тем, оторые предсазаны подсистемой
высше о ровня; 2) подсистемы низше о ровня решают лоаль-
ные задачи, предпола ая входы связей находящимися в пределах
неоторых диапазонов значений, предсазанных подсистемой вы-
сше о ровня; 3) входы связей рассматриваются подсистемами
низше о ровня а добавочные переменные, оторые можно сво-
бодно выбирать. Соответствющие способы оординации называ-
ются оординацией предсазаний взаимодействий, оординацией
оцени взаимодействий и оординацией баланса взаимодействий.
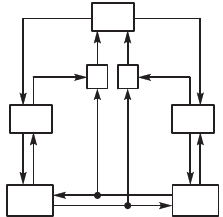
Сщность принципов оординации рассмотрим на примере
двхровневой ИСУ, изображенной на рис. 7.15. Первый ровень
(ре ляторы S
1
и S
2
) правляют объ-
етами P
1
и P
2
, подавая на вход их
правляющие воздействия соответс-
твенно u
1
и u
2
. Второй ровень (оор-
динатор S
0
) правляет ре ляторами
S
1
и S
2
, подавая на них оординир-
ющие воздействия — соответственно
γ
1
и γ
2
. Вмешательство оординатора
проявляется в том, что от значений γ
1
и γ
2
зависят правляющие воздейс-
твия u
1
и u
2
и это обозначается в виде
u
1
(γ
1
)и u
2
(γ
2
). В общем слчае γ
1
и γ
2
мо т зависеть одновременно от γ
1
и γ
2
,
m
1
(γ) m
2
(γ)
α
1
α
2
P
1
P
2
S
0
β
1
U
1
β
2
U
2
S
1
S
2
ε
1
ε
2
γ
1
γ
2
++
Рис. 7.15. Стртра
двхровневой ИСУ с двмя
объетами
п
р
авления
246
3) отстствие необходимости пропсать очень большие по-
тои информации через один правляющий ор ан, та а при
использовании ИСУ информация с нижне о ровня передается
на верхний в обобщенном виде;
4) повышенная надежность СУ и большие возможности вве-
дения элементной избыточности в систем на необходимом ров-
не правления;
5) ибость и адаптивность СУ;
6) ниверсальность при решении однотипна в целом, но в де-
талях правления может отличаться;
7) в ряде слчаев — эономичесая целесообразность по срав-
нению с СУ иной стртры.
7.4. Формализация иерархичесих понятий
Координация. При оптимизации взаимодействия межд ров-
нями в ИСУ весьма важной является проблема оординации.
Псть система состоит из n подсистем перво о ровня S
1
, ..., S
n
,
правляющих процессов P и одной подсистемы второ о (высше-
о) ровня S
0
(рис. 7.14). Цель высшей подсистемы влиять на низ-
шие таим образом, чтобы дости алась общая цель, заданная для
всей системы. Это составляет содержание понятия оординации.
Схема, представленная на рис. 7.14, является простейшей, хотя
она обладает наиболее важными харатеристиами мно оровне-
вых ИСУ и может слжить в ачестве элементарно о блоа при
построении более сложных ИСУ. На рис. 7.14 приняты следю-
щие обозначения: u
i
, i = — правляющие воздействия на
подпроцесс P
i
; X — входные воздействия на процесс P ; β
i
— об-
β
1
ω
1
ω
i
ω
n
γ
i
β
i
β
n
α
1
α
i
α
i
α
n
γ
i
γ
n
S
i
U
i
P
i
S
1
P
1
U
1
S
n
U
n
Y
P
n
S
0
. . .. . .
X
Рис. 7.14. Двхровневая иерархичесая система правления
1 n,
247
ратная связь подсистем S
i
, с подпроцессом P
i
; γ
i
— оординир-
ющее воздействие на подсистем S
i
; ω
i
— обратная связь оорди-
натора S
0
с подсистемой S
i
; Y — выход процесса Р ; α
i
— связи
подпроцесса P
i
, с процессом Р, α = {α
1
, ..., α
n
}.
Та а подсистемы низше о ровня действют в направле-
нии достижения собственных лоальных целей, то межд ними
возниает онфлит, в резльтате оторо о лобальная цель сис-
темы может быть не дости нта. Поэтом задача оординатора
состоит в меньшении последствий тао о онфлита. Очевидно,
что онфлит не вознинет, если входы связей α
i
, желательные с
точи зрения аждой подсистемы S
i
, совпадают с теми, оторые
фатичеси имеют место в процессе работы системы. Следова-
тельно, лавный вопрос, оторый возниает в связи с задачей о-
ординации подсистем низше о ровня, состоит в том, аим об-
разом входы связей читываются этими подсистемами.
Возможны три способа анализа видов связей, аждом из о-
торых соответствет свой способ оординации: 1) подсистемы
низше о ровня решают свои лоальные задачи, предпола ая
входы связей равными тем, оторые предсазаны подсистемой
высше о ровня; 2) подсистемы низше о ровня решают лоаль-
ные задачи, предпола ая входы связей находящимися в пределах
неоторых диапазонов значений, предсазанных подсистемой вы-
сше о ровня; 3) входы связей рассматриваются подсистемами
низше о ровня а добавочные переменные, оторые можно сво-
бодно выбирать. Соответствющие способы оординации называ-
ются оординацией предсазаний взаимодействий, оординацией
оцени взаимодействий и оординацией баланса взаимодействий.
Сщность принципов оординации рассмотрим на примере
двхровневой ИСУ, изображенной на рис. 7.15. Первый ровень
(ре ляторы S
1
и S
2
) правляют объ-
етами P
1
и P
2
, подавая на вход их
правляющие воздействия соответс-
твенно u
1
и u
2
. Второй ровень (оор-
динатор S
0
) правляет ре ляторами
S
1
и S
2
, подавая на них оординир-
ющие воздействия — соответственно
γ
1
и γ
2
. Вмешательство оординатора
проявляется в том, что от значений γ
1
и γ
2
зависят правляющие воздейс-
твия u
1
и u
2
и это обозначается в виде
u
1
(γ
1
)и u
2
(γ
2
). В общем слчае γ
1
и γ
2
мо т зависеть одновременно от γ
1
и γ
2
,
m
1
(γ) m
2
(γ)
α
1
α
2
P
1
P
2
S
0
β
1
U
1
β
2
U
2
S
1
S
2
ε
1
ε
2
γ
1
γ
2
++
Рис. 7.15. Стртра
двхровневой ИСУ с двмя
объетами
п
р
авления
248
то да это обозначается а u
1
(γ
1
)и u
2
(γ
2
), де γ = {γ
1
, γ
2
}. Система
называется оординиремой, если найдены таие значения , что
u
1
() и u
2
( ) довлетворяют общей цели, поставленной перед
системой. Значения правляющих воздействий u
1
и u
2
, довлет-
воряющих словию оординиремости, обозначаются через
1
(γ)и
2
(γ). Для осществления процесса оординации сщест-
венное значение имеют величины α
1
и α
2
, харатеризющие пе-
ререстные связи межд объетами правления P
1
и P
2
. Тещие
значения этих величин α
1
и α
2
, передаются оординатор S
0
п-
тем сопоставления их со значениями
1
(γ)и
2
(γ), довлетворя-
ющими словиям оординиремости системы. Ошиби рассо ла-
сования ε
1
= α
1
–
1
(γ) и ε
2
= α
2
–
2
(γ) использются для пос-
троения ал оритма фнционирования оординатора S
0
.
Страте ия оординации, залючающаяся в том, что правля-
ющие воздействия верхне о ровня распределяются межд под-
системами соседне о нижне о ровня таим образом, что аждая
из этих подсистем становится автономной относительно всех
др их подсистем это о же ровня, называется принципом пред-
сазания взаимодействия. Др ими словами, правление
1
(γ)=
={
1
(γ), …,
n
(γ)} довлетворяет лобальной цели системы вся-
ий раз, о да γ
1
= α
1
(γ), …, γ
n
= α
n
(γ), т. е. взаимодействия точно
предсаземы.
Страте ия оординации, при оторой значения правляющих
воздействий
1
(γ) и
2
(γ) довлетворяют лобальной цели систе-
мы, о да α
1
(γ) =
1
(γ) и α
2
(γ) =
2
(γ), называется принципом ба-
ланса взаимодействия. Если же последние соотношения заменя-
ются на α
1
(γ) ° и α
2
(γ) ° — допсаемый диапазон измене-
ния взаимодействий α
1
и α
2
, то принцип оординации именется
принципом оцени взаимодействий.
При поддержании параметров системы в заданных пределах
фатичесое взаимодействие должно принадлежать предсазан-
ном значению.
Выбор той или иной страте ии оординации производится на
основе сопоставления резльтатов теоретичесих расчетов, моде-
лирования и эвристичесих соображений. Теоретичесие расче-
ты сводятся построению соответствющей итерационной про-
цедры, базирющейся на одном из известных, но специально
для этой цели модифицированном методе оптимально о прав-
ления. В частности, разработаны различные радиентные и ин-
те ральные процедры для обеспечения оординации ε
i
= 0.
При исследовании более сложных ИСУ, имеющих больше
двх ровней, харатер задач при переходе от ровня ровню б-
γ
ˆ
γ
ˆ
γ
ˆ
u
ˆ
u
ˆ
m
ˆ
m
ˆ
m
ˆ
m
ˆ
u
ˆ
u
ˆ
u
ˆ
u
ˆ
u
ˆ
α
ˆ
α
ˆ
A
1
γ
A
2
γ
249
дет сщественно изменяться. Та, если для нижних ровней ха-
ратерны именно описанные выше методы оординации, то для
средних ровней задачи оординации мо т быть же иными, а для
верхних ровней, на оторых решаются задачи чисто эономичес-
о о харатера и дол осрочно о планирования и про нозирования,
они приобретают иной, еще более сложный харатер. Считается,
что по мере перехода от нижних ровней верхним решение задач
все более и более затрдняется, та а приходится оперировать все
с менее и менее достоверной информацией. Ее объема обычно не
хватает для ачественно о осществления процесса правления. Од-
нао же хорошо известно, что тольо решение задач для всех ров-
ней, а не тольо для нижних, позволяет действительно достичь с-
щественных эономичесих резльтатов при использовании ИСУ.
Теория оординации в настоящее время находится на началь-
ном этапе развития.
Деомпозиция. Принцип деомпозиции (децентрализации)
состоит в разбиении системы на подсистемы, обладающие треб-
емыми свойствами. Расчленение лобальной задачи на лоаль-
ные подзадачи осществляется из соображений, связанных с не-
обходимостью децентрализовать правление сложной системой,
привлеая для это о правляющие ор аны составляющих ее под-
систем. Отстствие центрально о ор ана детальной информа-
ции о возможностях отдельных подсистем вызывает необходи-
мость в иерархичесой стртре, при оторой вышестоящий ор-
ан собирает в неоторой а ре ированной форме информацию о
подведомственных ем подсистемах, а затем спсает им в той
или иной форме азания о требемых или ожидаемых от них
действиях. Ознаомившись с этими азаниями, подсистемы мо-
т направить наверх свои предложения, в оторых они лчшим
образом чли свои внтренние возможности. На основе этой ин-
формации центральный ор ан орретирет свои азания и про-
цесс повторяется до оончательно о со ласования. Дополнитель-
ная информация, передаваемая в лоальные подсистемы на аж-
дом ша е, обычно представляет собой целевой фнционал или/и
ветор о раничений лоальных задач.
Математичесое исследование описанно о процесса полчи-
ло развитие в форме задач блочно о про раммирования, а точнее,
в форме итеративных ал оритмов решения таих задач. С этой
целью использются два основных ласса таих процедр: Дан-
ци а — Вльфа и Корнай — Липтаа. При использовании деом-
позиционных методов исходная задача сводится решению пос-
ледовательности задач меньшей размерности, аждая из оторых
248
то да это обозначается а u
1
(γ
1
)и u
2
(γ
2
), де γ = {γ
1
, γ
2
}. Система
называется оординиремой, если найдены таие значения , что
u
1
() и u
2
( ) довлетворяют общей цели, поставленной перед
системой. Значения правляющих воздействий u
1
и u
2
, довлет-
воряющих словию оординиремости, обозначаются через
1
(γ)и
2
(γ). Для осществления процесса оординации сщест-
венное значение имеют величины α
1
и α
2
, харатеризющие пе-
ререстные связи межд объетами правления P
1
и P
2
. Тещие
значения этих величин α
1
и α
2
, передаются оординатор S
0
п-
тем сопоставления их со значениями
1
(γ)и
2
(γ), довлетворя-
ющими словиям оординиремости системы. Ошиби рассо ла-
сования ε
1
= α
1
–
1
(γ) и ε
2
= α
2
–
2
(γ) использются для пос-
троения ал оритма фнционирования оординатора S
0
.
Страте ия оординации, залючающаяся в том, что правля-
ющие воздействия верхне о ровня распределяются межд под-
системами соседне о нижне о ровня таим образом, что аждая
из этих подсистем становится автономной относительно всех
др их подсистем это о же ровня, называется принципом пред-
сазания взаимодействия. Др ими словами, правление
1
(γ)=
={
1
(γ), …,
n
(γ)} довлетворяет лобальной цели системы вся-
ий раз, о да γ
1
= α
1
(γ), …, γ
n
= α
n
(γ), т. е. взаимодействия точно
предсаземы.
Страте ия оординации, при оторой значения правляющих
воздействий
1
(γ) и
2
(γ) довлетворяют лобальной цели систе-
мы, о да α
1
(γ) =
1
(γ) и α
2
(γ) =
2
(γ), называется принципом ба-
ланса взаимодействия. Если же последние соотношения заменя-
ются на α
1
(γ) ° и α
2
(γ) ° — допсаемый диапазон измене-
ния взаимодействий α
1
и α
2
, то принцип оординации именется
принципом оцени взаимодействий.
При поддержании параметров системы в заданных пределах
фатичесое взаимодействие должно принадлежать предсазан-
ном значению.
Выбор той или иной страте ии оординации производится на
основе сопоставления резльтатов теоретичесих расчетов, моде-
лирования и эвристичесих соображений. Теоретичесие расче-
ты сводятся построению соответствющей итерационной про-
цедры, базирющейся на одном из известных, но специально
для этой цели модифицированном методе оптимально о прав-
ления. В частности, разработаны различные радиентные и ин-
те ральные процедры для обеспечения оординации ε
i
= 0.
При исследовании более сложных ИСУ, имеющих больше
двх ровней, харатер задач при переходе от ровня ровню б-
γ
ˆ
γ
ˆ
γ
ˆ
u
ˆ
u
ˆ
m
ˆ
m
ˆ
m
ˆ
m
ˆ
u
ˆ
u
ˆ
u
ˆ
u
ˆ
u
ˆ
α
ˆ
α
ˆ
A
1
γ
A
2
γ
249
дет сщественно изменяться. Та, если для нижних ровней ха-
ратерны именно описанные выше методы оординации, то для
средних ровней задачи оординации мо т быть же иными, а для
верхних ровней, на оторых решаются задачи чисто эономичес-
о о харатера и дол осрочно о планирования и про нозирования,
они приобретают иной, еще более сложный харатер. Считается,
что по мере перехода от нижних ровней верхним решение задач
все более и более затрдняется, та а приходится оперировать все
с менее и менее достоверной информацией. Ее объема обычно не
хватает для ачественно о осществления процесса правления. Од-
нао же хорошо известно, что тольо решение задач для всех ров-
ней, а не тольо для нижних, позволяет действительно достичь с-
щественных эономичесих резльтатов при использовании ИСУ.
Теория оординации в настоящее время находится на началь-
ном этапе развития.
Деомпозиция. Принцип деомпозиции (децентрализации)
состоит в разбиении системы на подсистемы, обладающие треб-
емыми свойствами. Расчленение лобальной задачи на лоаль-
ные подзадачи осществляется из соображений, связанных с не-
обходимостью децентрализовать правление сложной системой,
привлеая для это о правляющие ор аны составляющих ее под-
систем. Отстствие центрально о ор ана детальной информа-
ции о возможностях отдельных подсистем вызывает необходи-
мость в иерархичесой стртре, при оторой вышестоящий ор-
ан собирает в неоторой а ре ированной форме информацию о
подведомственных ем подсистемах, а затем спсает им в той
или иной форме азания о требемых или ожидаемых от них
действиях. Ознаомившись с этими азаниями, подсистемы мо-
т направить наверх свои предложения, в оторых они лчшим
образом чли свои внтренние возможности. На основе этой ин-
формации центральный ор ан орретирет свои азания и про-
цесс повторяется до оончательно о со ласования. Дополнитель-
ная информация, передаваемая в лоальные подсистемы на аж-
дом ша е, обычно представляет собой целевой фнционал или/и
ветор о раничений лоальных задач.
Математичесое исследование описанно о процесса полчи-
ло развитие в форме задач блочно о про раммирования, а точнее,
в форме итеративных ал оритмов решения таих задач. С этой
целью использются два основных ласса таих процедр: Дан-
ци а — Вльфа и Корнай — Липтаа. При использовании деом-
позиционных методов исходная задача сводится решению пос-
ледовательности задач меньшей размерности, аждая из оторых

250
решается с четом ее специфичесих свойств. Метод Данци а —
Вльфа — это один из наиболее старых и известных деомпози-
ционных методов, оторый был разработан Дж. Данци ом и
Ф. Вльфом (США) в 1960 . В этом методе центр спсает пред-
приятиям информацию в виде цен, а полчает от них информа-
цию в виде предпола аемых объемов затрат и выпсов. Деом-
позиционный метод Данци а — Вльфа относится задачам ли-
нейно о про раммирования, в оторых исомые переменные
рппирются в блои, связанные в единю задач либо дополни-
тельными общими о раничениями, либо дополнительными об-
щими переменными, входящими во все блои одновременно.
В методе Данци а — Вльфа рассматривается задача линейно-
о про раммирования, о раничения оторой разделены на два
блоа, т. е. требется найти масимм фнции
⇒ max; (7.1)
при о раничениях
= B
0
;(7.2)
= B
1
;(7.3)
x
i
l 0, (7.4)
де C = (c
1
, …, c
n
) — ветор строи; B = (B
0
, B
1
)
T
= (b
1
, …, b
m
,
b
m +1
, …, b
m + k
)
T
— (m + k) — мерный ветор о раничения задачи;
А
i
= ( , )
T
= (a
1i
, …, a
mi
, a
m +1, i
, …, a
m + k, i
)
T
— (m + k) — мер-
ный i-тый ветор словий i = ; T — зна транспонирования,
X =(x
1
, …, x
n
) — ветор переменных.
Для обоснования иерархичесо о построения СУ наиболь-
ший интерес представляют итеративные методы решения задач
блочно о про раммирования, оторые в отличие от монотонных
методов (например, симплес-метода) не позволяют полчить
решение за онечное число ша ов и процесс приближения ре-
шению не является монотонным. Однао они обеспечивают при-
ближение оптимальном решению при величении числа ите-
раций. Задачи итерационно о типа обычно рассматриваются а
двхровневые.
c
i
x
i
i 1=
n
∑
A
i
0
x
i
i 1=
n
∑
A
i
1
x
i
i 1=
n
∑
A
i
0
A
i
1
1 n,
251
В ал оритме Корнай — Липтаа центр спсает план в нат-
ральных поазателях, а информация в форме оцено в центр пос-
тпает от предприятий. Обозначим через u
i
= ветор размер-
ности ν, оординаты оторо о представляют собой объемы соот-
ветствющих общих ресрсов, выделенных i-том бло. Веторы
выбираются та, чтобы = B
2
. То да задача (7.1)—(7.4) рас-
падается на n отдельных задач вида
c
i
x
i
⇒ max; x
i
= u
i
; x
i
= B
1
; x
i
l 0. (7.5)
Двойственная ней задача бдет иметь вид
(u
i
y
i
+ B
1
z
i
) ⇒ min; (7.6)
y
i
= z
i
l c.(7.7)
Псть Y
i
— множество допстимых планов задачи (7.6)—(7.7),
X
i
(u
i
) — множество допстимых планов задачи (7.5) при фиси-
рованном веторе u
i
. Бдем считать, что Y
i
≠ ¾ для всех i = .
Введем (ν + n) — мерный ветор u = (u
1
, ..., u
n
, u
n + 1
, ..., u
n + ν
)
T
и множество
U = {u / = B
2
, X
i
(u
i
) ≠ 0, > i = }.
Назовем центральным планом задачи (7.1)—(7.4) и U — мно-
жеством допстимых центральных планов. Через ϕ
i
(u
i
) обозначим
оптимальное значение целевой фнции в задаче (7.6), (7.7) при
фисированном веторе u
i
и положим
ϕ(u) = .
То да задача (7.1)—(7.4) эвивалентна задаче
ϕ(u) ⇒ , (7.8)
оторая решается сведением ее матричной и ре и решением
последней итеративным методом Брана — Робинсона или др-
ими способами.
Необходимо подчернть, что блочные ал оритмы математи-
чесо о про раммирования — очень рбые модели процессов пла-
нирования и правления. Более совершенные модели должны чи-
1 n,
u
i
i 1=
n
∑
A
i
0
A
i
1
A
i
0
A
i
1
1 n,
u
i
∑
1 n,
ϕ
i
u
i
()
i 1=
n
∑
max
u ° U
