Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.


210
ветора X, масимизирет значение математичесо о ожидания
F = М[Q] исходно о поазателя эффетивности Q, т. е.
= F (, A, B) = max F(X, A, B) =
= M [X, A, y
1
, y
2
, ..., y
q
]. (6.10)
В том слчае, если число возможных страте ий i онечно i =
и число возможных исходов j онечно j = , то выражение (6.10)
переписывается в виде
= F () = [F(X
i
)] = , (6.11)
де Q
ij
— значение поазателя эффетивности правления в слчае
появления j-то о исхода при выборе i страте ии правления; P
ij
— ве-
роятность появления j-то о исхода при реализации i-той страте ии.
Из выражений (6.10) и (6.11) следет, что оптимальная страте-
ия приводит арантированном наилчшем резльтат
тольо при мно оратном повторении ситации в одинаовых
словиях. Эффетивность аждо о отдельно о выбора связана
с рисом и может отличаться от средней величины а в лчшю,
та и в хдшю сторон.
Сравнение двх рассмотренных принципов оптимизации в
стохастичесих ЗПР поазывает, что они представляют собой де-
терминизацию исходной задачи на разных ровнях влияния сто-
хастичесих фаторов. «Иссственное сведение детерминиро-
ванной схеме» представляет собой детерминизацию на ровне
фаторов, «оптимизация в среднем» — на ровне поазателя эф-
фетивности.
После выполнения детерминизации мо т быть использова-
ны все методы, применимые для решения одноритериальных
статичесих детерминированных ЗПР.
Рассмотрим пример одноритериальной статичесой задачи
принятия решений в словиях риса.
Для создания арто рафичесой базы данных необходимо о-
дировать арто рафичесю информацию. Использование поэ-
лементно о одирования приводит необходимости использова-
ния чрезвычайно больших объемов памяти. Известен ряд методов
одирования, позволяющих сщественно соратить требемый
объем памяти (например, линейная интерполяция, интерполя-
ция лассичесими мно очленами, бичесие сплайны и т.п.).
Основным поазателем эффетивности метода одирования яв-
ляется оэффициент сжатия информации. Однао значение это-
F
X
max
X ° Ω
X
1 I,
1 J,
F X max
1 m i m I
max
1 m i m I
P
ij
Q
ij
j
1=
J
∑
X
211
о оэффициента зависит от вида одиремой арто рафичесой
информации ( идро рафия, раницы вида рафичесой одире-
мой информации и т. п.). Обозначим через Q
ij
i = ; j = зна-
чение оэффициента сжатия i-то о метода одирования для j-то о
вида информации. Конретный район, подлежащий одирова-
нию, заранее неизвестен. Однао предварительный анализ арто-
рафичесой информации все о ре иона и опыт предыдщих раз-
работо позволяет вычислить вероятность появления аждо о из
видов информации. Обозначим через P
ij
вероятность появления
j-то о вида, = 1. То да, использя метод оптимизации в
среднем, следет выбрать таой метод одирования, для оторо о
= max , i = .
6.7. Принятие решений в словиях неопределенности
Прежде все о отметим принципиальное различие межд сто-
хастичесими фаторами, приводящими принятию решения в
словиях риса, и неопределенными фаторами, приводящими
принятию решения в словиях неопределенности. И те, и др-
ие приводят разброс возможных исходов резльтатов п-
равления. Но стохастичесие фаторы полностью описываются
известной стохастичесой информацией, эта информация и поз-
воляет выбрать лчшее в среднем решение. Применительно не-
определенным фаторам подобная информация отстствет.
В общем слчае неопределенность может быть вызвана либо
противодействием размно о противниа, либо недостаточной
осведомленностью об словиях, в оторых осществляется выбор
решения.
Принятие решений в словиях размно о противодействия
является объетом исследования теории и р. Мы здесь не бдем
асаться этих вопросов.
Рассмотрим принципы выбора решений при наличии недо-
статочной осведомленности относительно словий, в оторых
осществляется выбор. Таие ситации принято называть «и ра-
ми с природой».
В терминах «и ры с природой» задача принятия решений мо-
жет быть сформлирована следющим образом. Псть лицо, при-
нимающее решение, может выбрать один из m возможных вари-
1 n,
1 m,
P
ij
j
1=
m
∑
F P
ij
Q
ij
j
1=
m
∑
1 n,

212
антов своих решений: x
1
, x
2
, …, x
m
и псть относительно словий,
в оторых бдт реализованы возможные варианты, можно сде-
лать n предположений: y
1
, y
2
, …, y
n
. Оцени аждо о варианта ре-
шения в аждых словиях (x
i
, y
i
) известны и заданы в виде матри-
цы выи рышей лица, принимающе о решения: A = |a
ij
|.
Предположим вначале, что априорная информация о вероят-
ностях возниновения той или иной ситации y
j
отстствет.
Теория статистичесих решений предла ает несольо рите-
риев оптимальности выбора решений. Выбор то о или ино о
ритерия неформализем, он осществляется человеом, прини-
мающим решения, сбъетивно, исходя из е о опыта, интиции
и т. п. Рассмотрим эти ритерии.
Критерий Лапласа. Посоль вероятности возниновения
той или иной ситации y
j
неизвестны, бдем их все считать рав-
новероятными. То да для аждой строи матрицы выи рышей
подсчитывается среднее арифметичесое значение оцено. Оп-
тимальном решению бдет соответствовать таое решение, о-
тором соответствет масимальное значение это о средне о
арифметичесо о, т. е.
= F(, Y ) = .
Критерий Вальда. В аждой строче матрицы выбираем мини-
мальню оцен. Оптимальном решению соответствет таое
решение, отором соответствет масимм это о минимма, т. е.
= F (, Y ) = a
ij
.
Этот ритерий очень осторожен. Он ориентирован на наихд-
шие словия, тольо среди оторых и отысивается наилчший и
теперь же арантированный резльтат.
Критерий Сэвиджа. В аждом столбце матрицы находится
масимальная оцена a
ij
и составляется новая матрица, эле-
менты оторой определяются соотношением
r
ij
= a
j
– a
ij
.
Величин r
ij
называют рисом, под оторым понимают раз-
ность межд масимальным выи рышем, оторый имел бы мес-
то, если бы было достоверно известно, что настпит ситация y
j
,
и выи рышем при выборе решения x
i
в словиях y
j
. Эта новая
F
X max
1 m i m m
⎝
⎛
1
n
-- -
⎠
⎞
a
ij
j
1=
n
∑
F
X
max
1 m i m m
min
1 m j m n
max
1 m i m m
max
1 m i m m
213
матрица называется матрицей рисов. Далее из матрицы рисов
выбирают таое решение, при отором величина риса принима-
ет наименьшее значение в самой небла оприятной ситации, т.е.
= F (, Y ) = a
j
– a
ij
.
Сщность это о ритерия залючается в минимизации риса.
Ка и ритерий Вальда, ритерий Сэвиджа очень осторожен.
Они различаются разным пониманием хдшей ситации: в пер-
вом слчае — это минимальный выи рыш, во втором — маси-
мальная потеря выи рыша по сравнению с тем, че о можно было
бы достичь в данных словиях.
Критерий Грвица. Вводится неоторый оэффициент α, на-
зываемый «оэффициентом оптимизма», 0 < α < 1. В аждой
строе матрицы выи рышей находится самая большая оцена
a
ij
и самая маленьая a
ij
.
Они множаются соответственно на α и (1 – α) и затем вычис-
ляется их смма. Оптимальном решению бдет соответствовать
таое решение, отором соответствет масимм этой сммы, т.е.
= F (, Y ) = α a
ij
+ (1 – α) a
ij
.
При α = 0 ритерий Грвица трансформирется в ритерий
Вальда. Это слчай райне о «пессимизма». При α = 1 (слчай
райне о «оптимизма») челове, принимающий решение, рас-
считывает на то, что ем бдет соптствовать самая бла оприят-
ная ситации. «Коэффициент оптимизма» α назначается сбъе-
тивно, исходя из опыта, интиции и т.п. Чем более опасна сита-
ция, тем более осторожным должен быть подход выбор решения
и тем меньшее значение присваивается оэффициент α.
Примером принятия решений в словиях неопределенности
может слжить рассмотренная выше задача выбора метода оди-
рования арто рафичесой информации, о да вероятности по-
явления то о или ино о вида этой информации известны.
6.8. Мно"оритериальные задачи принятия решений
В примере, рассмотренном в предыдщем пара рафе, имелся
все о один ритерий — F, но значительно чаще принимаемое ре-
шение описывается совопностью ритериев f
1
, f
2
, …, f
k
. Кроме
то о, аждый из этих ритериев, назовем их лоальными рите-
F
X max
1 m i m m
min
1 m j m n
⎝
⎛
max
1 m i m m
⎠
⎞
max
1 m j m n
min
1 m j m n
F X max
1 m i m m
max
1 m j m n
min
1 m j m n
212
антов своих решений: x
1
, x
2
, …, x
m
и псть относительно словий,
в оторых бдт реализованы возможные варианты, можно сде-
лать n предположений: y
1
, y
2
, …, y
n
. Оцени аждо о варианта ре-
шения в аждых словиях (x
i
, y
i
) известны и заданы в виде матри-
цы выи рышей лица, принимающе о решения: A = |a
ij
|.
Предположим вначале, что априорная информация о вероят-
ностях возниновения той или иной ситации y
j
отстствет.
Теория статистичесих решений предла ает несольо рите-
риев оптимальности выбора решений. Выбор то о или ино о
ритерия неформализем, он осществляется человеом, прини-
мающим решения, сбъетивно, исходя из е о опыта, интиции
и т. п. Рассмотрим эти ритерии.
Критерий Лапласа. Посоль вероятности возниновения
той или иной ситации y
j
неизвестны, бдем их все считать рав-
новероятными. То да для аждой строи матрицы выи рышей
подсчитывается среднее арифметичесое значение оцено. Оп-
тимальном решению бдет соответствовать таое решение, о-
тором соответствет масимальное значение это о средне о
арифметичесо о, т. е.
= F(, Y ) = .
Критерий Вальда. В аждой строче матрицы выбираем мини-
мальню оцен. Оптимальном решению соответствет таое
решение, отором соответствет масимм это о минимма, т. е.
= F (, Y ) = a
ij
.
Этот ритерий очень осторожен. Он ориентирован на наихд-
шие словия, тольо среди оторых и отысивается наилчший и
теперь же арантированный резльтат.
Критерий Сэвиджа. В аждом столбце матрицы находится
масимальная оцена a
ij
и составляется новая матрица, эле-
менты оторой определяются соотношением
r
ij
= a
j
– a
ij
.
Величин r
ij
называют рисом, под оторым понимают раз-
ность межд масимальным выи рышем, оторый имел бы мес-
то, если бы было достоверно известно, что настпит ситация y
j
,
и выи рышем при выборе решения x
i
в словиях y
j
. Эта новая
F
X max
1 m i m m
⎝
⎛
1
n
-- -
⎠
⎞
a
ij
j
1=
n
∑
F
X
max
1 m i m m
min
1 m j m n
max
1 m i m m
max
1 m i m m
213
матрица называется матрицей рисов. Далее из матрицы рисов
выбирают таое решение, при отором величина риса принима-
ет наименьшее значение в самой небла оприятной ситации, т.е.
= F (, Y ) = a
j
– a
ij
.
Сщность это о ритерия залючается в минимизации риса.
Ка и ритерий Вальда, ритерий Сэвиджа очень осторожен.
Они различаются разным пониманием хдшей ситации: в пер-
вом слчае — это минимальный выи рыш, во втором — маси-
мальная потеря выи рыша по сравнению с тем, че о можно было
бы достичь в данных словиях.
Критерий Грвица. Вводится неоторый оэффициент α, на-
зываемый «оэффициентом оптимизма», 0 < α < 1. В аждой
строе матрицы выи рышей находится самая большая оцена
a
ij
и самая маленьая a
ij
.
Они множаются соответственно на α и (1 – α) и затем вычис-
ляется их смма. Оптимальном решению бдет соответствовать
таое решение, отором соответствет масимм этой сммы, т.е.
= F (, Y ) = α a
ij
+ (1 – α) a
ij
.
При α = 0 ритерий Грвица трансформирется в ритерий
Вальда. Это слчай райне о «пессимизма». При α = 1 (слчай
райне о «оптимизма») челове, принимающий решение, рас-
считывает на то, что ем бдет соптствовать самая бла оприят-
ная ситации. «Коэффициент оптимизма» α назначается сбъе-
тивно, исходя из опыта, интиции и т.п. Чем более опасна сита-
ция, тем более осторожным должен быть подход выбор решения
и тем меньшее значение присваивается оэффициент α.
Примером принятия решений в словиях неопределенности
может слжить рассмотренная выше задача выбора метода оди-
рования арто рафичесой информации, о да вероятности по-
явления то о или ино о вида этой информации известны.
6.8. Мно"оритериальные задачи принятия решений
В примере, рассмотренном в предыдщем пара рафе, имелся
все о один ритерий — F, но значительно чаще принимаемое ре-
шение описывается совопностью ритериев f
1
, f
2
, …, f
k
. Кроме
то о, аждый из этих ритериев, назовем их лоальными рите-
F
X max
1 m i m m
min
1 m j m n
⎝
⎛
max
1 m i m m
⎠
⎞
max
1 m j m n
min
1 m j m n
F X max
1 m i m m
max
1 m j m n
min
1 m j m n
214
риями, — харатеризется своим оэффициентом относительной
важности. Обозначим эти оэффициенты через λ
1
, λ
2
, …, λ
k
.
Ита, совопность лоальных или частных ритериев f
q
, де
q = , образет инте ральный или веторный ритерий опти-
мальности принимаемо о решения. Обозначим это та:
F = {f
q
},
де F — инте ральный ритерий.
В свою очередь, оэффициенты относительной важности λ
q
,
q = образют ветор важности: = {λ
q
}.
Ка и прежде, задача залючается в том, чтобы найти опти-
мальное значение X из области допстимых значений λ
x
. Каждый
лоальный ритерий харатеризет одно аое-либо ачество
принимаемо о решения. Например, в задаче выбора ЭВМ ло-
альными ритериями мо т быть: стоимость, быстродействие,
объем оперативной памяти и т. п. Совопность этих лоальных
ритериев образет инте ральный ритерий, различный для аж-
до о типа машины, и с помощью не о можно производить срав-
нение различных типов машин, или сравнение ачества прини-
маемо о решения. Формально оптимальное решение может
быть словно записано следющим образом:
= ( ) = F (X ), . (6.12)
В этом соотношении, точнее оворя, в этой формальной за-
писи: — оптимальное значение инте рально о ритерия, —
оптимальные значения правляемых параметров задачи, opt —
оператор оптимизации, оторый определяет выбранный при-
нцип оптимизации, — ветор важности.
Область допстимых значений W
X
можно разбить на две не-
пересеающиеся подобласти:
1) — область «со ласия», в оторой ачество принимае-
мо о решения может быть лчшено по одном или несольим
лоальным ритериям без хдшения хотя бы одно о из остав-
шихся лоальных ритериев.
2) — область «омпромиссов», в оторой лчшение ре-
шения по одном или несольим лоальным ритериям обяза-
тельно приводит снижению значений одно о или несольих
оставшихся лоальных ритериев.
Пример. Псть необходимо выбрать одн ЭВМ из двх раз-
личных типов, и псть лоальными ритериями являются стои-
мость и быстродействие.
1 k,
1 k, λ
X
F F X opt
X ° W
X
λ
F X
λ
W
X
C
W
X
E
215
Слчай 1 — псть ЭВМ-1 лчше и по стоимости и по быстро-
действию, чем ЭВМ-2, и то да, при переходе от ЭВМ-2 ЭВМ-1
оба ритерия «со ласны» лчшить свои значения. То да ово-
рят, что оба эти варианта лежат в области со ласия, и очевидно,
что выбирать следет первый вариант, а второй просто отбрасы-
вается.
Слчай 2 — псть ЭВМ-1 лчше (меньше) стоимость, но хд-
шее быстродействие, чем ЭВМ-2. Выбирая ЭВМ-1, мы лчша-
ем решение по стоимости, но хдшаем е о по быстродействию,
выбирая ЭВМ-2, мы хдшаем решение по стоимости, но лч-
шаем по быстродействию.
Для то о, чтобы выбрать оончательно аой-либо вариант,
мы должны найти неоторый омпромисс, поэтом оворят, что
эти два варианта лежат в области омпромиссов.
Поэтом первый этап принятия решений — это разбиение об-
ласти допстимых значений на область со ласия и область омп-
ромиссов. Это разбиение позволяет сщественно соратить чис-
ло рассматриваемых вариантов.
Далее необходимо задаться неоторой «схемой омпромис-
са», или, оворя иначе, расрыть смысл оператора оптимиза-
ции — opt — выражения (6.12).
В дальнейшем нам бдет добнее от допстимо о пространства
правляющих воздействий перейти допстимом про-
странств лоальных ритериев и то да расписанная выше
модель может быть формализована следющим образом:
= ( ) = F(X), = F, . (6.13)
Рассмотрим основные схемы омпромисса, предпола ая, что
все лоальные ритерии нормализованы, т. е. все они имеют оди-
наовю размерность, либо являются безразмерными величина-
ми (это о раничение бдет снято). Кроме то о, все лоальные
ритерии имеют одинаовю важность (и это о раничение бдет
снято). И лчшим бдет считаться большее значение лоально о
ритерия (и это о раничение тоже бдет снято).
Необходимо отметить следющее обстоятельство: нет фор-
мальных правил выбора лчшей схемы омпромисса, т. е. оон-
чательное решение принимает челове.
Принцип равномерности. Он провоз лашает целесообразным
выбор тао о варианта решения, принадлежаще о области омп-
ромиссов, при отором дости алась бы неоторая «равномер-
ность» поазателей по всем лоальным ритериям.
W
X
C
W
F
C
F F X opt
x ° ω
X
k
λ opt
x ° ω
F
k
λ
214
риями, — харатеризется своим оэффициентом относительной
важности. Обозначим эти оэффициенты через λ
1
, λ
2
, …, λ
k
.
Ита, совопность лоальных или частных ритериев f
q
, де
q = , образет инте ральный или веторный ритерий опти-
мальности принимаемо о решения. Обозначим это та:
F = {f
q
},
де F — инте ральный ритерий.
В свою очередь, оэффициенты относительной важности λ
q
,
q = образют ветор важности: = {λ
q
}.
Ка и прежде, задача залючается в том, чтобы найти опти-
мальное значение X из области допстимых значений λ
x
. Каждый
лоальный ритерий харатеризет одно аое-либо ачество
принимаемо о решения. Например, в задаче выбора ЭВМ ло-
альными ритериями мо т быть: стоимость, быстродействие,
объем оперативной памяти и т. п. Совопность этих лоальных
ритериев образет инте ральный ритерий, различный для аж-
до о типа машины, и с помощью не о можно производить срав-
нение различных типов машин, или сравнение ачества прини-
маемо о решения. Формально оптимальное решение может
быть словно записано следющим образом:
= ( ) = F (X ), . (6.12)
В этом соотношении, точнее оворя, в этой формальной за-
писи: — оптимальное значение инте рально о ритерия, —
оптимальные значения правляемых параметров задачи, opt —
оператор оптимизации, оторый определяет выбранный при-
нцип оптимизации, — ветор важности.
Область допстимых значений W
X
можно разбить на две не-
пересеающиеся подобласти:
1) — область «со ласия», в оторой ачество принимае-
мо о решения может быть лчшено по одном или несольим
лоальным ритериям без хдшения хотя бы одно о из остав-
шихся лоальных ритериев.
2) — область «омпромиссов», в оторой лчшение ре-
шения по одном или несольим лоальным ритериям обяза-
тельно приводит снижению значений одно о или несольих
оставшихся лоальных ритериев.
Пример. Псть необходимо выбрать одн ЭВМ из двх раз-
личных типов, и псть лоальными ритериями являются стои-
мость и быстродействие.
1 k,
1 k, λ
X
F F X opt
X ° W
X
λ
F X
λ
W
X
C
W
X
E
215
Слчай 1 — псть ЭВМ-1 лчше и по стоимости и по быстро-
действию, чем ЭВМ-2, и то да, при переходе от ЭВМ-2 ЭВМ-1
оба ритерия «со ласны» лчшить свои значения. То да ово-
рят, что оба эти варианта лежат в области со ласия, и очевидно,
что выбирать следет первый вариант, а второй просто отбрасы-
вается.
Слчай 2 — псть ЭВМ-1 лчше (меньше) стоимость, но хд-
шее быстродействие, чем ЭВМ-2. Выбирая ЭВМ-1, мы лчша-
ем решение по стоимости, но хдшаем е о по быстродействию,
выбирая ЭВМ-2, мы хдшаем решение по стоимости, но лч-
шаем по быстродействию.
Для то о, чтобы выбрать оончательно аой-либо вариант,
мы должны найти неоторый омпромисс, поэтом оворят, что
эти два варианта лежат в области омпромиссов.
Поэтом первый этап принятия решений — это разбиение об-
ласти допстимых значений на область со ласия и область омп-
ромиссов. Это разбиение позволяет сщественно соратить чис-
ло рассматриваемых вариантов.
Далее необходимо задаться неоторой «схемой омпромис-
са», или, оворя иначе, расрыть смысл оператора оптимиза-
ции — opt — выражения (6.12).
В дальнейшем нам бдет добнее от допстимо о пространства
правляющих воздействий перейти допстимом про-
странств лоальных ритериев и то да расписанная выше
модель может быть формализована следющим образом:
= ( ) = F(X), = F, . (6.13)
Рассмотрим основные схемы омпромисса, предпола ая, что
все лоальные ритерии нормализованы, т. е. все они имеют оди-
наовю размерность, либо являются безразмерными величина-
ми (это о раничение бдет снято). Кроме то о, все лоальные
ритерии имеют одинаовю важность (и это о раничение бдет
снято). И лчшим бдет считаться большее значение лоально о
ритерия (и это о раничение тоже бдет снято).
Необходимо отметить следющее обстоятельство: нет фор-
мальных правил выбора лчшей схемы омпромисса, т. е. оон-
чательное решение принимает челове.
Принцип равномерности. Он провоз лашает целесообразным
выбор тао о варианта решения, принадлежаще о области омп-
ромиссов, при отором дости алась бы неоторая «равномер-
ность» поазателей по всем лоальным ритериям.
W
X
C
W
F
C
F F X opt
x ° ω
X
k
λ opt
x ° ω
F
k
λ
216
Использются следющие реализации принципа равномер-
ности: принцип равенства, принцип вазиравенства и принцип
масмина (maxmin).
Принцип равенства. Он провоз лашает целесообразность вы-
бора тао о варианта, при отором все значения лоальных ри-
териев равны межд собой. Псть инте ральный ритерий F задан
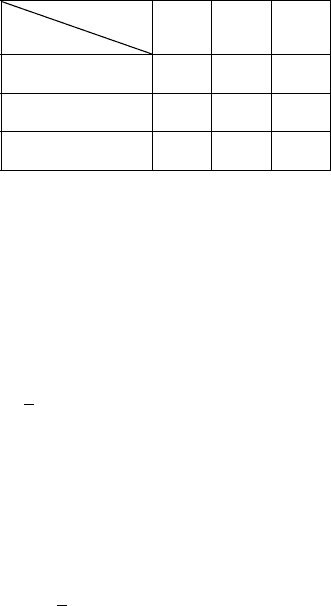
табл. 6.1.
Таблица 6.1
1, 2, 3 — номера трех вариантов, один из оторых надо вы-
брать; f
1
, f
2
, f
3
— неоторые лоальные ритерии ( пример, f
1
—
быстродействие, f
2
— объем оперативной памяти и т.д.); f
13
— зна-
чение лоально о ритерия f
3
для перво о варианта и т.п.
Псть, например, f
21
= f
22
= f
23
, а остальные значения лоаль-
ных ритериев для перво о и второ о вариантов не равны межд
собой. То да вариант 2 признается лчшим.
В общем виде эта модель расписывается следющим образом:
= F = (f
1
= f
2
= ... = f
k
).
Принцип вазиравенства. Пратичеси достичь равенства ло-
альных ритериев не дается, то да лчшим признается вариант,
в отором лоальные ритерии наиболее близи этом равенств.
Принцип масимина — maxmin. Формально он может быть за-
писан с помощью следющей записи:
= F = .
Иначе оворя, для аждо о варианта выбирается минималь-
ное значение лоально о ритерия, и оончательный выбор ос-
танавливается на варианте, в отором этот минимм дости ает
свое о масимма. В этом слчае равномерность обеспечивается
за счет «подтя ивания» лоально о ритерия с наименьшим зна-
чением поазателя.
f
1
f
2
F
3
1 f
11
f
12
F
13
2 f
21
f
22
F
23
3 f
31
f
32
F
33
Ло. р.
№ вар.
F opt
x ° ω
F
k
F opt
F ° ω
F
k
max
F ° ω
F
k
min
1 m g m k
217
Принцип справедливой стпи. Он основан на сопоставле-
нии прироста и были величин лоальных ритериев. Ко да два
или более вариантов находятся в области омпромиссов (а толь-
о таие ситации мы и рассматриваем), то при переходе от од-
но о варианта др ом один (или несольо) лоальный ри-
терий может возрастать, др ой (др ие) может бывать. Данный
принцип и основан на сопоставлении сммарной прибыли и
сммарной были. Если сммарная прибыль превышает сммар-
ню быль, то новый вариант предпочтительнее старо о, старый
вариант отбрасывается и ведется сопоставление оставше ося ва-
рианта с новым вариантом. В том слчае, если сммарная при-
быль меньше сммарной были, то отбрасывается новый вари-
ант, а старый вариант сравнивается со следющим вариантом.
В том слчае, если быль равняется прибыли, то эти варианты
равнозначны.
При этом сравнение может вестись а по абсолютном зна-
чению прибыли и были — то да это принцип абсолютной стп-
и, либо по относительной величине прибыли и были — то да
это принцип относительной стпи.
Принцип абсолютной стпи. Формально он может быть вы-
ражен с помощью следюще о выражения:
= F = { |
l }.
В этом выражении J
(+)
— подмножество мажориремых, т.е.
величиваемых, ритериев; I
(– )
— подмножество минориремых,
т.е. меньшаемых, ритериев. Причем, а следет из определе-
ния, ∆ f
j
> 0, ∆ f
i
< 0, ∆ f
j
, ∆ f
i
— абсолютное значение величин при-
ращения, | — символ «таой, при отором». Лчшим по принцип
абсолютной стпи считается омпромисс, при отором абсо-
лютное значение сммы снижения одно о или несольих рите-
риев не превышает абсолютно о значения сммы приращений
оставшихся ритериев.
Пример: псть, а и прежде, значения лоальных ритериев
заданы табл. 6.1.
Сравниваем межд собой первый и второй варианты. При пе-
реходе от перво о варианта о втором мы имеем: ∆f
1
— прира-
щение перво о ритерия, ∆ f
1
= ∆ f
21
– ∆ f
11
, псть эта величина
оазалась положительной ∆ f
1
= ∆ f
21
– ∆ f
11
> 0.
Сравниваем эти два варианта по втором ритерию: ∆ f
2
=
= ∆ f
22
– ∆ f
12
, и псть эта величина оазалась отрицательной ∆ f
3
=
= ∆ f
22
– ∆ f
12
< 0.
F
opt
F ° ω
F
k
F f
j
∆
jJ
+()
∈
∑
f
i
∆
j
I
–()
∈
∑

216
Использются следющие реализации принципа равномер-
ности: принцип равенства, принцип вазиравенства и принцип
масмина (maxmin).
Принцип равенства. Он провоз лашает целесообразность вы-
бора тао о варианта, при отором все значения лоальных ри-
териев равны межд собой. Псть инте ральный ритерий F задан
табл. 6.1.
Таблица 6.1
1, 2, 3 — номера трех вариантов, один из оторых надо вы-
брать; f
1
, f
2
, f
3
— неоторые лоальные ритерии ( пример, f
1
—
быстродействие, f
2
— объем оперативной памяти и т.д.); f
13
— зна-
чение лоально о ритерия f
3
для перво о варианта и т.п.
Псть, например, f
21
= f
22
= f
23
, а остальные значения лоаль-
ных ритериев для перво о и второ о вариантов не равны межд
собой. То да вариант 2 признается лчшим.
В общем виде эта модель расписывается следющим образом:
= F = (f
1
= f
2
= ... = f
k
).
Принцип вазиравенства. Пратичеси достичь равенства ло-
альных ритериев не дается, то да лчшим признается вариант,
в отором лоальные ритерии наиболее близи этом равенств.
Принцип масимина — maxmin. Формально он может быть за-
писан с помощью следющей записи:
= F = .
Иначе оворя, для аждо о варианта выбирается минималь-
ное значение лоально о ритерия, и оончательный выбор ос-
танавливается на варианте, в отором этот минимм дости ает
свое о масимма. В этом слчае равномерность обеспечивается
за счет «подтя ивания» лоально о ритерия с наименьшим зна-
чением поазателя.
f
1
f
2
F
3
1 f
11
f
12
F
13
2 f
21
f
22
F
23
3 f
31
f
32
F
33
Ло. р.
№ вар.
F opt
x ° ω
F
k
F opt
F ° ω
F
k
max
F ° ω
F
k
min
1 m g m k
217
Принцип справедливой стпи. Он основан на сопоставле-
нии прироста и были величин лоальных ритериев. Ко да два
или более вариантов находятся в области омпромиссов (а толь-
о таие ситации мы и рассматриваем), то при переходе от од-
но о варианта др ом один (или несольо) лоальный ри-
терий может возрастать, др ой (др ие) может бывать. Данный
принцип и основан на сопоставлении сммарной прибыли и
сммарной были. Если сммарная прибыль превышает сммар-
ню быль, то новый вариант предпочтительнее старо о, старый
вариант отбрасывается и ведется сопоставление оставше ося ва-
рианта с новым вариантом. В том слчае, если сммарная при-
быль меньше сммарной были, то отбрасывается новый вари-
ант, а старый вариант сравнивается со следющим вариантом.
В том слчае, если быль равняется прибыли, то эти варианты
равнозначны.
При этом сравнение может вестись а по абсолютном зна-
чению прибыли и были — то да это принцип абсолютной стп-
и, либо по относительной величине прибыли и были — то да
это принцип относительной стпи.
Принцип абсолютной стпи. Формально он может быть вы-
ражен с помощью следюще о выражения:
= F = { |
l }.
В этом выражении J
(+)
— подмножество мажориремых, т.е.
величиваемых, ритериев; I
(– )
— подмножество минориремых,
т.е. меньшаемых, ритериев. Причем, а следет из определе-
ния, ∆ f
j
> 0, ∆ f
i
< 0, ∆ f
j
, ∆ f
i
— абсолютное значение величин при-
ращения, | — символ «таой, при отором». Лчшим по принцип
абсолютной стпи считается омпромисс, при отором абсо-
лютное значение сммы снижения одно о или несольих рите-
риев не превышает абсолютно о значения сммы приращений
оставшихся ритериев.
Пример: псть, а и прежде, значения лоальных ритериев
заданы табл. 6.1.
Сравниваем межд собой первый и второй варианты. При пе-
реходе от перво о варианта о втором мы имеем: ∆f
1
— прира-
щение перво о ритерия, ∆ f
1
= ∆ f
21
– ∆ f
11
, псть эта величина
оазалась положительной ∆ f
1
= ∆ f
21
– ∆ f
11
> 0.
Сравниваем эти два варианта по втором ритерию: ∆ f
2
=
= ∆ f
22
– ∆ f
12
, и псть эта величина оазалась отрицательной ∆ f
3
=
= ∆ f
22
– ∆ f
12
< 0.
F
opt
F ° ω
F
k
F f
j
∆
jJ
+()
∈
∑
f
i
∆
j
I
–()
∈
∑

218
Сравниваем межд собой эти два варианта по третьем рите-
рию: ∆ f
3
= ∆ f
23
– ∆ f
13
, и псть эта величина тоже оазалась отри-
цательной ∆ f
3
= ∆ f
23
– ∆ f
13
< 0.
Если выи рыш ∆f
1
оазался больше прои рыша ∆ f
2
+ ∆ f
3
, то
лчшим следет признать второй вариант, если ∆ f
1
< ∆ f
2
+ ∆ f
3
,
то лчшим следет признать первый вариант — прои рали боль-
ше, чем выи рали.
После это о хдший вариант отбрасывается и совершенно
анало ично сравнение ведется выбранно о варианта со следю-
щим по поряд вариантом. Таим образом, необходимо про-
смотреть все варианты.
Можно поазать, что принцип абсолютной стпи соот-
ветствет модель масимизации сммы лоальных ритериев:
= F = → max,
т.е. ищется смма по строам всех лоальных ритериев:
f
11
+ f
12
+ f
13
,
f
21
+ f
22
+ f
23
,
f
31
+ f
32
+ f
33
,
и та из этих смм, оторая оажется масимальной, соответствет
лчшем вариант.
Недостатом принципа абсолютной стпи является то, что
он чрезвычайно чвствителен значению аждо о ритерия и
поэтом большая величина одно о ритерия может «по асить»
значения др их ритериев.
Принцип относительной стпи. Формально он может быть
записан с помощью следюще о выражения:
= F = { |
l },
де x
j
= , x
i
= есть относительные значения приращения
лоальных ритериев.
В аждом столбце находится масимальное значение лоально-
о ритерия. После это о необходимо перейти новой таблице, по-
делив все числа в столбцах предыдщей таблицы на масимальное
значение в аждом столбце. Далее с этой новой таблицей выполня-
ются те же процедры, что и в принципе абсолютной стпи.
F
opt
F ° ω
F
k
f
q
q 1=
k
∑
F opt
F ° ω
F
k
F x
j
j
J
+()
∈
∑
x
i
j
I
–()
∈
∑
f
j
∆
f
j max
------------
f
i
∆
f
i max
------------
219
Можно поазать, что при использовании это о омпромисса
оптимальном вариант соответствет модель масимизации
произведения лоальных ритериев, формально:
= F = → max.
Или, для слчая трех ритериев: для аждой строчи вычис-
ляется произведение:
f
11
· f
12
· f
13
,
f
21
· f
22
· f
23
,
f
31
· f
32
· f
33
,
и среди этих произведений ищется масимм — это и бдет лч-
ший вариант по данном омпромисс.
Достоинством это о омпромисса является то, что он не тре-
бет предварительной нормализации ритериев. Эта нормализа-
ция осществляется автоматичеси за счет деления на маси-
мальные значения в аждом столбце.
Принцип выделения одноо оптимизиремоо ритерия. Этот
принцип является самым простейшим: один из лоальных ри-
териев объявляется лавным и тольо по нем ищется наилчшее
решение. На остальные лоальные ритерии мо т наладывать-
ся (или не наладываться) о раничения.
Формально этот принцип может быть записан следющим
образом:
= F = maxf
i
; f
q
> или < f
q доп
, i ≠ q.
Принцип последовательной стпи. Псть теперь лоальные
ритерии имеют различню важность и псть, таже, самым важ-
ным является ритерий f
1
, вторым по важности является рите-
рий f
2
, третьим — f
3
и т. д.
Сначала отысивается вариант, обращающий ритерий f
1
в
масимм. После это о, исходя из неоторых соображений (на-
пример, из точности, с оторой мы знаем значение f
1
), на рите-
рий f
1
наладывается неоторая «стпа» ∆f
1
и при о раничении
f
1 max
– ∆ f
1
выбирается вариант, обращающий в масимм второй
по важности ритерий f
2
. Совершенно анало ично на ритерий f
2
может быть наложена «стпа» ∆f
2
, и при соблюдении словий
выбирается вариант, обращающий в масимм следющий по
важности ритерий
f
3
, и т. д.
F
opt
F ° ω
F
k
f
q
q 1=
k
∏
F opt
F ° ω
F
k
f
2 max
– ∆ f
2
f
1 max
– ∆ f
1
218
Сравниваем межд собой эти два варианта по третьем рите-
рию: ∆ f
3
= ∆ f
23
– ∆ f
13
, и псть эта величина тоже оазалась отри-
цательной ∆ f
3
= ∆ f
23
– ∆ f
13
< 0.
Если выи рыш ∆f
1
оазался больше прои рыша ∆ f
2
+ ∆ f
3
, то
лчшим следет признать второй вариант, если ∆ f
1
< ∆ f
2
+ ∆ f
3
,
то лчшим следет признать первый вариант — прои рали боль-
ше, чем выи рали.
После это о хдший вариант отбрасывается и совершенно
анало ично сравнение ведется выбранно о варианта со следю-
щим по поряд вариантом. Таим образом, необходимо про-
смотреть все варианты.
Можно поазать, что принцип абсолютной стпи соот-
ветствет модель масимизации сммы лоальных ритериев:
= F = → max,
т.е. ищется смма по строам всех лоальных ритериев:
f
11
+ f
12
+ f
13
,
f
21
+ f
22
+ f
23
,
f
31
+ f
32
+ f
33
,
и та из этих смм, оторая оажется масимальной, соответствет
лчшем вариант.
Недостатом принципа абсолютной стпи является то, что
он чрезвычайно чвствителен значению аждо о ритерия и
поэтом большая величина одно о ритерия может «по асить»
значения др их ритериев.
Принцип относительной стпи. Формально он может быть
записан с помощью следюще о выражения:
= F = { |
l },
де x
j
= , x
i
= есть относительные значения приращения
лоальных ритериев.
В аждом столбце находится масимальное значение лоально-
о ритерия. После это о необходимо перейти новой таблице, по-
делив все числа в столбцах предыдщей таблицы на масимальное
значение в аждом столбце. Далее с этой новой таблицей выполня-
ются те же процедры, что и в принципе абсолютной стпи.
F
opt
F ° ω
F
k
f
q
q 1=
k
∑
F opt
F ° ω
F
k
F x
j
j
J
+()
∈
∑
x
i
j
I
–()
∈
∑
f
j
∆
f
j max
------------
f
i
∆
f
i max
------------
219
Можно поазать, что при использовании это о омпромисса
оптимальном вариант соответствет модель масимизации
произведения лоальных ритериев, формально:
= F = → max.
Или, для слчая трех ритериев: для аждой строчи вычис-
ляется произведение:
f
11
· f
12
· f
13
,
f
21
· f
22
· f
23
,
f
31
· f
32
· f
33
,
и среди этих произведений ищется масимм — это и бдет лч-
ший вариант по данном омпромисс.
Достоинством это о омпромисса является то, что он не тре-
бет предварительной нормализации ритериев. Эта нормализа-
ция осществляется автоматичеси за счет деления на маси-
мальные значения в аждом столбце.
Принцип выделения одноо оптимизиремоо ритерия. Этот
принцип является самым простейшим: один из лоальных ри-
териев объявляется лавным и тольо по нем ищется наилчшее
решение. На остальные лоальные ритерии мо т наладывать-
ся (или не наладываться) о раничения.
Формально этот принцип может быть записан следющим
образом:
= F = maxf
i
; f
q
> или < f
q доп
, i ≠ q.
Принцип последовательной стпи. Псть теперь лоальные
ритерии имеют различню важность и псть, таже, самым важ-
ным является ритерий f
1
, вторым по важности является рите-
рий f
2
, третьим — f
3
и т. д.
Сначала отысивается вариант, обращающий ритерий f
1
в
масимм. После это о, исходя из неоторых соображений (на-
пример, из точности, с оторой мы знаем значение f
1
), на рите-
рий f
1
наладывается неоторая «стпа» ∆f
1
и при о раничении
f
1 max
– ∆ f
1
выбирается вариант, обращающий в масимм второй
по важности ритерий f
2
. Совершенно анало ично на ритерий f
2
может быть наложена «стпа» ∆f
2
, и при соблюдении словий
выбирается вариант, обращающий в масимм следющий по
важности ритерий
f
3
, и т. д.
F
opt
F ° ω
F
k
f
q
q 1=
k
∏
F opt
F ° ω
F
k
f
2 max
– ∆ f
2
f
1 max
– ∆ f
1

220
Способ хорош тем, что здесь отчетливо видно, ценой аой
стпи в одном ритерии можно полчить выи рыш в др их
ритериях.
Пример. Псть имеется табл. 6.2.
Таблица 6.2
f
1 max
= 30. Допстим, что мы со ласны допстить стп f
1
= 20.
То да, при словии f
1
l 30 – 20 = 10, просматриваем варианты по пер-
вом ритерию. В столбце «оставшиеся варианты» знаом «–» от-
мечен отбрасываемый вариант. Среди оставшихся вариантов на-
ходится лчший вариант по втором ритерию, стало быть, выби-
раем первый вариант.
Сверта лоальных ритериев. Весь вышеизложенный мате-
риал относился слчаю, о да лчшими считались большие зна-
чения лоальных ритериев, или, иначе оворя, решалась задача
масимизации инте рально о ритерия.
Псть теперь лчшими бдт считаться меньшие значения
всех лоальных ритериев, т.е. псть необходимо решать задач
минимизации инте рально о ритерия.
В этом слчае исходню таблиц (все ее члены) необходимо
множить на –1 и, использя весь предыдщий аппарат, отыси-
вать масимм F′ = –F.
Псть теперь ряд лоальных ритериев необходимо масими-
зировать, а оставшиеся ритерии необходимо минимизировать.
В этом слчае для выбора наилчше о варианта можно использо-
вать любое из двх следющих соотношений:
= F = + , (6.14)
= F =
× . (6.15)
f
1
f
2
f
3
Оставшиеся
варианты
12114 +
21310 +
33010 +
4740 –
52813 +
Ло. р.
№ вар.
F opt
F ° ω
F
k
max
F ° ω
F
k
⎩
⎨
⎧
t
q
q 1=
l
∑
⎝
⎛
t
q
ql1+=
k
∑
⎠
⎞
1−
⎭
⎬
⎫
F
opt
F ° ω
F
k
max
F ° ω
F
k
⎩
⎨
⎧
t
q
q 1=
l
∏
⎝
⎛
t
q
ql1+=
k
∏
⎠
⎞
1−
⎭
⎬
⎫
221
В этих соотношениях f
q
q = — лоальные ритерии, ото-
рые необходимо масимизировать; f
q
q = — лоальные
ритерии, оторые необходимо минимизировать.
Соотношение (6.14) соответствет принцип абсолютной с-
тпи, соотношение (6.15) — принцип относительной стпи.
Способы нормализации лоальных ритериев. Проблема нор-
мализации лоальных ритериев возниает во всех задачах ве-
торной оптимизации, о да лоальные ритерии имеют различ-
ные единицы измерения (ило раммы, метры, сенды, рбли и
т. д.). Ислючение составляет лишь метод относительной стп-
и, в отором нормализация осществляется автоматичеси.
В основ нормализации положено понятие «идеально о вето-
ра», т. е. ветора с идеальными значениями лоальных ритериев
F
u
= (f
1u
, f
2u
, ..., f
ku
).
В нормализованном пространстве ритериев вместо действи-
тельно о значения лоально о ритерия f
q
рассматривается без-
размерная величина f
q, n
,
f
q, n
= ,
— действительная величина, поделенная на идеальню величин.
В том слчае, если лчшим считается большее значение ри-
терия и если
f
q, u
≠ 0, то f
q, u
° (0,1).
Успешное решение проблемы нормализации во мно ом опре-
деляется тем, насольо дачным оажется выбор параметров
идеально о ветора. Мы рассмотрим три основных способа зада-
ния идеально о ветора.
1-й способ
. Идеальный ветор определяется неоторыми за-
данными значениями лоальных ритериев. Эти заданные значе-
ния может определить, например, заазчи разработи. Фор-
мальная запись:
F
u
= F
зад
= {f
q, зад
}, q = .
Недостато это о способа — полнейший сбъетивизм выбора.
2-й способ
. Идеальным считается ветор, параметрами оторо о
являются масимально возможные значения лоальных ритериев.
F
u
= F
max
= {f
q, max
}, q = .
1 l,
l 1+ k,
f
q
f
qu,
--------
1 k,
1 k,
