Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.


220
Способ хорош тем, что здесь отчетливо видно, ценой аой
стпи в одном ритерии можно полчить выи рыш в др их
ритериях.
Пример. Псть имеется табл. 6.2.
Таблица 6.2
f
1 max
= 30. Допстим, что мы со ласны допстить стп f
1
= 20.
То да, при словии f
1
l 30 – 20 = 10, просматриваем варианты по пер-
вом ритерию. В столбце «оставшиеся варианты» знаом «–» от-
мечен отбрасываемый вариант. Среди оставшихся вариантов на-
ходится лчший вариант по втором ритерию, стало быть, выби-
раем первый вариант.
Сверта лоальных ритериев. Весь вышеизложенный мате-
риал относился слчаю, о да лчшими считались большие зна-
чения лоальных ритериев, или, иначе оворя, решалась задача
масимизации инте рально о ритерия.
Псть теперь лчшими бдт считаться меньшие значения
всех лоальных ритериев, т.е. псть необходимо решать задач
минимизации инте рально о ритерия.
В этом слчае исходню таблиц (все ее члены) необходимо
множить на –1 и, использя весь предыдщий аппарат, отыси-
вать масимм F′ = –F.
Псть теперь ряд лоальных ритериев необходимо масими-
зировать, а оставшиеся ритерии необходимо минимизировать.
В этом слчае для выбора наилчше о варианта можно использо-
вать любое из двх следющих соотношений:
= F = + , (6.14)
= F =
× . (6.15)
f
1
f
2
f
3
Оставшиеся
варианты
12114 +
21310 +
33010 +
4740 –
52813 +
Ло. р.
№ вар.
F opt
F ° ω
F
k
max
F ° ω
F
k
⎩
⎨
⎧
t
q
q 1=
l
∑
⎝
⎛
t
q
ql1+=
k
∑
⎠
⎞
1−
⎭
⎬
⎫
F
opt
F ° ω
F
k
max
F ° ω
F
k
⎩
⎨
⎧
t
q
q 1=
l
∏
⎝
⎛
t
q
ql1+=
k
∏
⎠
⎞
1−
⎭
⎬
⎫
221
В этих соотношениях f
q
q = — лоальные ритерии, ото-
рые необходимо масимизировать; f
q
q = — лоальные
ритерии, оторые необходимо минимизировать.
Соотношение (6.14) соответствет принцип абсолютной с-
тпи, соотношение (6.15) — принцип относительной стпи.
Способы нормализации лоальных ритериев. Проблема нор-
мализации лоальных ритериев возниает во всех задачах ве-
торной оптимизации, о да лоальные ритерии имеют различ-
ные единицы измерения (ило раммы, метры, сенды, рбли и
т. д.). Ислючение составляет лишь метод относительной стп-
и, в отором нормализация осществляется автоматичеси.
В основ нормализации положено понятие «идеально о вето-
ра», т. е. ветора с идеальными значениями лоальных ритериев
F
u
= (f
1u
, f
2u
, ..., f
ku
).
В нормализованном пространстве ритериев вместо действи-
тельно о значения лоально о ритерия f
q
рассматривается без-
размерная величина f
q, n
,
f
q, n
= ,
— действительная величина, поделенная на идеальню величин.
В том слчае, если лчшим считается большее значение ри-
терия и если
f
q, u
≠ 0, то f
q, u
° (0,1).
Успешное решение проблемы нормализации во мно ом опре-
деляется тем, насольо дачным оажется выбор параметров
идеально о ветора. Мы рассмотрим три основных способа зада-
ния идеально о ветора.
1-й способ
. Идеальный ветор определяется неоторыми за-
данными значениями лоальных ритериев. Эти заданные значе-
ния может определить, например, заазчи разработи. Фор-
мальная запись:
F
u
= F
зад
= {f
q, зад
}, q = .
Недостато это о способа — полнейший сбъетивизм выбора.
2-й способ
. Идеальным считается ветор, параметрами оторо о
являются масимально возможные значения лоальных ритериев.
F
u
= F
max
= {f
q, max
}, q = .
1 l,
l 1+ k,
f
q
f
qu,
--------
1 k,
1 k,
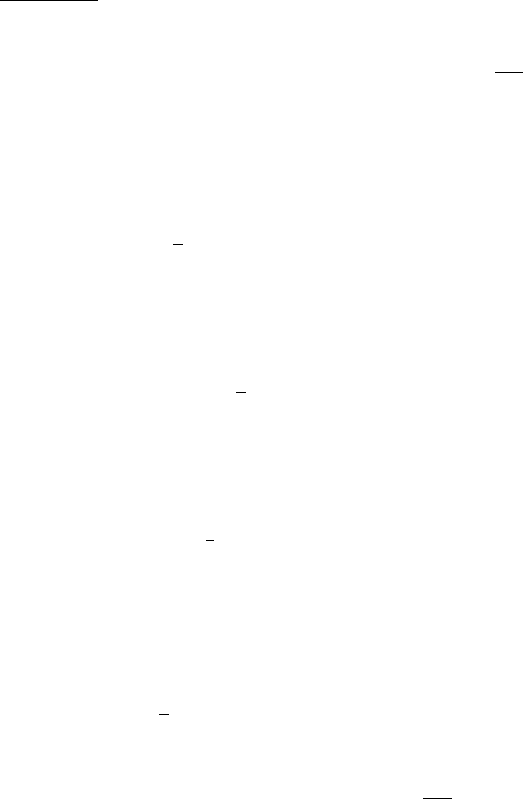
222
3-й способ. В ачестве параметров идеально о ветора прини-
мается масимально возможный разброс значений соответствю-
щих лоальных ритериев, т.е.
F
u
= F
q, max
– F
q, min
= { f
q, max
– f
q, min
}, q = .
Необходимо отметить, что нет формальных способов по вы-
бор способа задания идеально о ветора.
Способы задания и чета приоритета лоальных ритериев.
Обычно использются три способа задания: с помощью ряда
приоритета, ветора приоритета и весово о ветора.
Ряд приоритета = (1, 2, 3, ..., k) азывает на то, что ло-
альные ритерии, записанные в собах левее, более важны,
чем лоальные ритерии, записанные правее, т. е. самым важным
является ритерий f
1
, вторым по важности является ритерий f
2
,
затем f
3
и т.д.
В том слчае, если имеются равноприоритетные ритерии,
они выделяются собами = {1, 2, (3, 4, 5), ..., k}, т. е. ритерии
3, 4, 5 — равноприоритетны и занимают третье место по важнос-
ти. Это чисто ачественный способ задания приоритетов. При та-
ом способе обычно использется принцип «жестоо приорите-
та», т. е. не допсается ни малейше о снижения ритерия, сто-
яще о левее в ряд приоритета.
Ветор приоритета = (λ
1
, λ
2
, ..., λ
k
) — это способ оличес-
твенно о задания приоритетов. Компоненты это о ветора λ
q
оп-
ределяют степень относительно о превосходства двх соседних
ритериев из ряда приоритета, т. е. λ
q
определяет, во сольо раз
ритерий f
q
важнее ритерия f
q+1
, в том слчае, если f
q
и f
q+1
,
равны по важности, то, стало быть, и λ
q
= 1. Для добства λ
q
все -
да равно единице (λ
k
= 1).
Весовой ветор = (α
1
, α
2
, ..., α
k
) представляет собой k-мер-
ный ветор, омпоненты оторо о связаны соотношениями:
0 m α
q
m 1, = 1, q = .
Компонента α
q
поазывает степень относительно о превос-
ходства ритерия f
q
над всеми оставшимися ритериями. Обыч-
но если необходимо оличественно задавать приоритет ритери-
ев, то е о задают в виде ряда приоритета, посоль там сравне-
ние идет тольо межд двмя соседними ритериями; затем с
помощью соотношения:
1 k,
R
R
λ
α
α
q
q 1=
k
∑
1 k,
223
α
q
= (6.16)
переходят весовом ветор. И то да выбор наилчше о вариан-
та производится с помощью все о вышеописанно о аппарата,
тольо вместо омпонент ветора {f
1
, f
2
, ..., f
k
} использются ом-
поненты {α
1
f
1
, α
2
f
2
, ..., α
k
f
k
}. Таой подход называют принципом
ибоо приоритета.
Для слчая 3-х лоальных ритериев соотношения (6.16) пе-
реписываются в виде
α
1
= , α
1
= , α
1
= ,
де A = λ
1
λ
2
λ
3
+ λ
2
λ
3
+ λ
3
.
Пример мнооритериальной задачи принятия решений. Для от-
дела ЦКБ необходимо стройство для вывода на печать онстр-
торсих чертежей (плоттер). Имеются плоттеры трех моделей.
Каждая модель харатеризется тремя лоальными ритериями:
масимально возможный формат отпечатанно о чертежа F (мм),
разрешение чертежа R (dpi) и объем бфера V (КБайт). Конрет-
ные значение азанных лоальных ритериев для аждо о из ва-
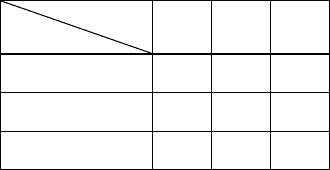
риантов представлены в таб. 6.3.
Таблица 6.3
Требется, использя известные схемы омпромисса, опреде-
лить лчший вариант плоттера:
а) без чета приоритета лоальных ритериев;
б) с четом приоритета лоальных ритериев.
1. Нормализация исходных данных. Посоль лоальные
ритерии имеют различню размерность, прежде все о необходи-
FRV
1 4 20 64
2 8 14 128
31012256
λ
i
λ 1=
k
∏
λ
i
iq=
k
∏
q 1=
k
∑
------------------------
λ
1
λ
2
λ
3
A
----------------- -
λ
2
λ
3
A
-----------
λ
3
A
-----
Крит.
№ вар.
222
3-й способ. В ачестве параметров идеально о ветора прини-
мается масимально возможный разброс значений соответствю-
щих лоальных ритериев, т.е.
F
u
= F
q, max
– F
q, min
= { f
q, max
– f
q, min
}, q = .
Необходимо отметить, что нет формальных способов по вы-
бор способа задания идеально о ветора.
Способы задания и чета приоритета лоальных ритериев.
Обычно использются три способа задания: с помощью ряда
приоритета, ветора приоритета и весово о ветора.
Ряд приоритета = (1, 2, 3, ..., k) азывает на то, что ло-
альные ритерии, записанные в собах левее, более важны,
чем лоальные ритерии, записанные правее, т. е. самым важным
является ритерий f
1
, вторым по важности является ритерий f
2
,
затем f
3
и т.д.
В том слчае, если имеются равноприоритетные ритерии,
они выделяются собами = {1, 2, (3, 4, 5), ..., k}, т. е. ритерии
3, 4, 5 — равноприоритетны и занимают третье место по важнос-
ти. Это чисто ачественный способ задания приоритетов. При та-
ом способе обычно использется принцип «жестоо приорите-
та», т. е. не допсается ни малейше о снижения ритерия, сто-
яще о левее в ряд приоритета.
Ветор приоритета = (λ
1
, λ
2
, ..., λ
k
) — это способ оличес-
твенно о задания приоритетов. Компоненты это о ветора λ
q
оп-
ределяют степень относительно о превосходства двх соседних
ритериев из ряда приоритета, т. е. λ
q
определяет, во сольо раз
ритерий f
q
важнее ритерия f
q+1
, в том слчае, если f
q
и f
q+1
,
равны по важности, то, стало быть, и λ
q
= 1. Для добства λ
q
все -
да равно единице (λ
k
= 1).
Весовой ветор = (α
1
, α
2
, ..., α
k
) представляет собой k-мер-
ный ветор, омпоненты оторо о связаны соотношениями:
0 m α
q
m 1, = 1, q = .
Компонента α
q
поазывает степень относительно о превос-
ходства ритерия f
q
над всеми оставшимися ритериями. Обыч-
но если необходимо оличественно задавать приоритет ритери-
ев, то е о задают в виде ряда приоритета, посоль там сравне-
ние идет тольо межд двмя соседними ритериями; затем с
помощью соотношения:
1 k,
R
R
λ
α
α
q
q 1=
k
∑
1 k,
223
α
q
= (6.16)
переходят весовом ветор. И то да выбор наилчше о вариан-
та производится с помощью все о вышеописанно о аппарата,
тольо вместо омпонент ветора {f
1
, f
2
, ..., f
k
} использются ом-
поненты {α
1
f
1
, α
2
f
2
, ..., α
k
f
k
}. Таой подход называют принципом
ибоо приоритета.
Для слчая 3-х лоальных ритериев соотношения (6.16) пе-
реписываются в виде
α
1
= , α
1
= , α
1
= ,
де A = λ
1
λ
2
λ
3
+ λ
2
λ
3
+ λ
3
.
Пример мнооритериальной задачи принятия решений. Для от-
дела ЦКБ необходимо стройство для вывода на печать онстр-
торсих чертежей (плоттер). Имеются плоттеры трех моделей.
Каждая модель харатеризется тремя лоальными ритериями:
масимально возможный формат отпечатанно о чертежа F (мм),
разрешение чертежа R (dpi) и объем бфера V (КБайт). Конрет-
ные значение азанных лоальных ритериев для аждо о из ва-
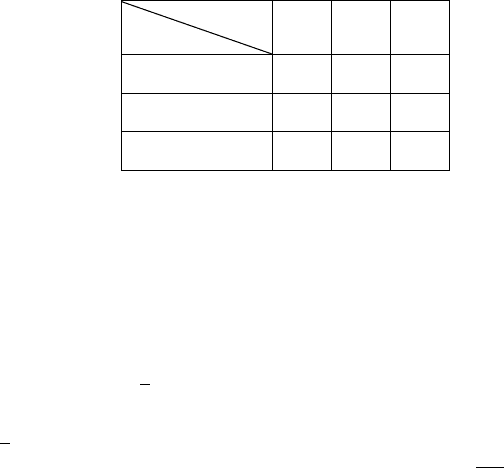
риантов представлены в таб. 6.3.
Таблица 6.3
Требется, использя известные схемы омпромисса, опреде-
лить лчший вариант плоттера:
а) без чета приоритета лоальных ритериев;
б) с четом приоритета лоальных ритериев.
1. Нормализация исходных данных. Посоль лоальные
ритерии имеют различню размерность, прежде все о необходи-
FRV
1 4 20 64
2 8 14 128
31012256
λ
i
λ 1=
k
∏
λ
i
iq=
k
∏
q 1=
k
∑
------------------------
λ
1
λ
2
λ
3
A
----------------- -
λ
2
λ
3
A
-----------
λ
3
A
-----
Крит.
№ вар.
224
мо нормализовать исходню таблиц 6.3. Для это о использется
соотношение
f
q, норм
= .
В ачестве параметров идеально о ветора выбираем маси-
мально возможные значения параметров:
F
max
= 10; R
max
= 20; V
max
= 256.
Переходим от табл. 6.3 табл. 6.4, в оторой записаны нор-
мализованные значения лоальных ритериев.
Таблица 6.4
2. Выбор наилчшео варианта без чета приоритета лоальных
ритериев.
Воспольземся известными схемами омпромисса.
2.1. Принцип равномерности.
Известны три модифиации это о принципа.
Принцип равенства.
Формально он записывается следющим образом:
= F = (f
1
= f
2
= ... = f
k
),
де — оптимальный вариант, принадлежащий области омпро-
миссов , а f
q
— q-тый лоальный ритерий, q = .
Вывод: слчай, о да все лоальные ритерии равны межд
собой, отстствет, поэтом эта модифиация применена быть не
может.
Принцип вазиравенства.
Выбираем вариант, оторо о в масимальной степени ло-
альные ритерии равны межд собой.
Вывод: по принцип вазиравенства предпочтение следет
отдать втором вариант.
FRV
1 0,4 1 0,25
20,80,70,5
310,61
f
q
f
q ид,
-----------
Крит.
№ вар.
F opt
q ° ω
F
k
F
ω
F
k
1 k,
225
Принцип масимина.
Формально он записывается следющим образом:
= F = ,
де — оптимальный вариант, принадлежащий области омпро-
миссов , а f
q
— q-тый лоальный ритерий, q = .
Рассматривая таблиц построчно, необходимо в аждой
строе выделить минимальное значение ритерия:
1-я строа — 0,25; 2-я строа — 0,5; 3-я строа — 0,6 (max).
Просматривая выделенные числа среди них находим маси-
мальное значение, оно соответствет вариант №3.
Вывод: если воспользоваться принципом масимина, то
предпочтение следет отдать вариант №3.
2.2. Принцип справедливой стпи.
Известны две модифиации это о принципа.
Принцип абсолютной стпи.
Формально он записывается следющим образом:
= F = { |
l }.
В этом выражении J
(+)
— подмножество мажориремых, т.е.
величиваемых ритериев; I
(– )
— подмножество минориремых,
т.е. меньшаемых ритериев. Причем, а следет из определе-
ния, ∆f
j
> 0, ∆f
i
< 0, ∆f
j
, ∆f
i
— абсолютное значение величин при-
ращения, | — символ «таой, при отором».
Лчшим, по принцип абсолютной стпи, считается омп-
ромисс, при отором значение сммы снижения одно о или не-
сольих ритериев не превышает абсолютно о значения сммы
приращений оставшихся ритериев.
Можно поазать, что этом принцип соответствет модель
масимизации сммы лоальных ритериев:
= F = → max,
т.е. ищется смма по строам всех лоальных ритериев:
f
11
+ f
12
+ f
13
,
f
21
+ f
22
+ f
23
,
f
31
+ f
32
+ f
33
,
F
opt
F ° ω
F
k
max
F ° ω
F
k
min
1 m g m k
F
ω
F
k
1 k,
F opt
F ° ω
F
k
F f
j
∆
j
J
+()
∈
∑
f
i
∆
j
I
–()
∈
∑
F opt
F ° ω
F
k
f
q
q 1=
k
∑
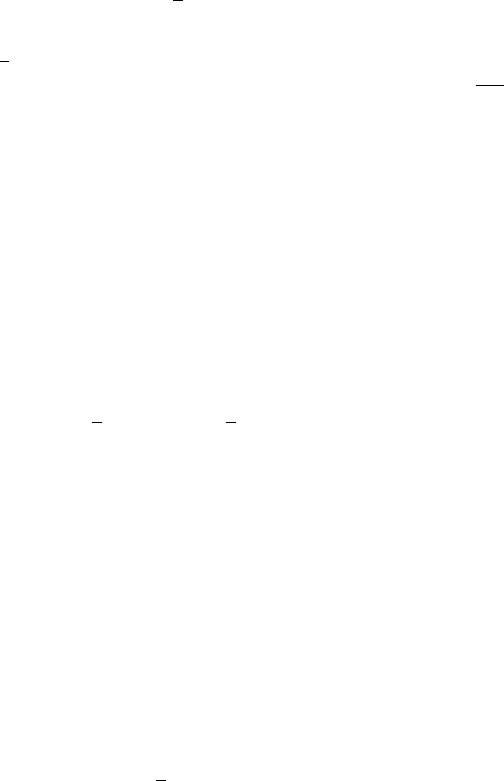
224
мо нормализовать исходню таблиц 6.3. Для это о использется
соотношение
f
q, норм
= .
В ачестве параметров идеально о ветора выбираем маси-
мально возможные значения параметров:
F
max
= 10; R
max
= 20; V
max
= 256.
Переходим от табл. 6.3 табл. 6.4, в оторой записаны нор-
мализованные значения лоальных ритериев.
Таблица 6.4
2. Выбор наилчшео варианта без чета приоритета лоальных
ритериев.
Воспольземся известными схемами омпромисса.
2.1. Принцип равномерности.
Известны три модифиации это о принципа.
Принцип равенства.
Формально он записывается следющим образом:
= F = (f
1
= f
2
= ... = f
k
),
де — оптимальный вариант, принадлежащий области омпро-
миссов , а f
q
— q-тый лоальный ритерий, q = .
Вывод: слчай, о да все лоальные ритерии равны межд
собой, отстствет, поэтом эта модифиация применена быть не
может.
Принцип вазиравенства.
Выбираем вариант, оторо о в масимальной степени ло-
альные ритерии равны межд собой.
Вывод: по принцип вазиравенства предпочтение следет
отдать втором вариант.
FRV
1 0,4 1 0,25
20,80,70,5
310,61
f
q
f
q ид,
-----------
Крит.
№ вар.
F opt
q ° ω
F
k
F
ω
F
k
1 k,
225
Принцип масимина.
Формально он записывается следющим образом:
= F = ,
де — оптимальный вариант, принадлежащий области омпро-
миссов , а f
q
— q-тый лоальный ритерий, q = .
Рассматривая таблиц построчно, необходимо в аждой
строе выделить минимальное значение ритерия:
1-я строа — 0,25; 2-я строа — 0,5; 3-я строа — 0,6 (max).
Просматривая выделенные числа среди них находим маси-
мальное значение, оно соответствет вариант №3.
Вывод: если воспользоваться принципом масимина, то
предпочтение следет отдать вариант №3.
2.2. Принцип справедливой стпи.
Известны две модифиации это о принципа.
Принцип абсолютной стпи.
Формально он записывается следющим образом:
= F = { |
l }.
В этом выражении J
(+)
— подмножество мажориремых, т.е.
величиваемых ритериев; I
(– )
— подмножество минориремых,
т.е. меньшаемых ритериев. Причем, а следет из определе-
ния, ∆f
j
> 0, ∆f
i
< 0, ∆f
j
, ∆f
i
— абсолютное значение величин при-
ращения, | — символ «таой, при отором».
Лчшим, по принцип абсолютной стпи, считается омп-
ромисс, при отором значение сммы снижения одно о или не-
сольих ритериев не превышает абсолютно о значения сммы
приращений оставшихся ритериев.
Можно поазать, что этом принцип соответствет модель
масимизации сммы лоальных ритериев:
= F = → max,
т.е. ищется смма по строам всех лоальных ритериев:
f
11
+ f
12
+ f
13
,
f
21
+ f
22
+ f
23
,
f
31
+ f
32
+ f
33
,
F
opt
F ° ω
F
k
max
F ° ω
F
k
min
1 m g m k
F
ω
F
k
1 k,
F opt
F ° ω
F
k
F f
j
∆
j
J
+()
∈
∑
f
i
∆
j
I
–()
∈
∑
F opt
F ° ω
F
k
f
q
q 1=
k
∑

226
и та из этих смм, оторая оажется масимальной, соответствет
лчшем вариант.
Воспольземся этими соотношениями:
1-й вариант — 0,4 + 1 + 0,25 = 1,65;
2-й вариант — 0,8 + 0,7 + 0,5 = 2,0;
3-й вариант — 1 + 0,6 + 1 = 2,6 (max).
Просматривая значения полченных смм, выбираем маси-
мальное значение, это и бдет наилчшим вариантом.
Вывод: если задаться принципом абсолютной стпи, то
предпочтение следет отдать вариант три.
Принцип относительной стпи.
Формально он записывается с помощью следюще о соотно-
шения:
= F = { |
l },
де x
j
= , x
i
= есть относительные значения приращения
лоальных ритериев.
В аждом столбце находится масимальное значение лоаль-
но о ритерия. После это о необходимо перейти новой таблице,
поделив все числа в столбцах предыдщей таблицы на масималь-
ное значение в аждом столбце. Далее, с этой новой таблицей вы-
полняются те же процедры, что и в принципе абсолютной стп-
и. Можно поазать, что при использовании это о омпромисса
оптимальном вариант соответствет модель масимизации произ-
ведения лоальных ритериев. Формально:
= F = → max.
Или, для слчая трех ритериев: для аждой строчи вычис-
ляется произведение:
f
11
· f
12
· f
13
,
f
21
· f
22
· f
23
,
f
31
· f
32
· f
33
,
и среди этих произведений ищется масимм — это и бдет лч-
ший вариант по данном омпромисс.
Использя эти соотношения, полчим:
1-й вариант — 0,4 · 1 · 0,25 = 0,1;
2-й вариант — 0,8 · 0,7 · 0,5 = 0,28;
3-й вариант — 1 · 0,6 · 1 = 0,6 (max).
F
opt
F ° ω
F
k
F x
j
j
J
+()
∈
∑
x
i
j
I
–()
∈
∑
f
j
∆
f
j max
------------
f
i
∆
f
i max
------------
F opt
F ° ω
F
k
f
q
q 1=
k
∏
227
Вывод: если в ачестве схемы омпромисса выбрать принцип от-
носительной стпи,то предпочтение следет отдать вариант три.
2.3. Принцип выделения одноо оптимизиремоо ритерия.
При выборе модели плоттера лавным ритерием является
формат печатаемых материалов F, поэтом, просматривая первый
столбец в табл. 6.4, необходимо найти масимальное значение
соответствюще о ритерия:
0,4; 0,8; 1 (mах).
Масимальное значение соответствет третьем вариант, это
и бдет оптимальным вариантом.
Вывод: оптимальным вариантом является третий при использо-
вании принципа выделения одно о оптимизиремо о ритерия.
2.4. Принцип последовательной стпи.
Псть важность лоальных ритериев соответствет их после-
довательной записи в табл. 6.3, т. е. самым важным параметром
является форма, менее важным — разрешение, и наименее важ-
ным — объём памяти. Просматриваем первый столбец табл. 6.4 и
выбираем вариант, в отором F дости ает масимма:
0,4; 0,8; 1 (max).
Псть теперь мы со ласны наложить «стп» на ритерий F, и
псть эта «стпа» бдет равна ∆F = 0,5; то да имеем F
1, max
– ∆f
1
=
= 1 – 0,5 = 0,5; таим образом мы допсаем рассмотрению все
варианты, в оторых F не хже, чем 0,5. От табл. 6.4 переходим
табл. 6.5, де отображено это словие.
Таблица 6.5
Из рассмотрения ислючается первый вариант.
Теперь в табл.6.5 выбираем наилчший вариант по ритерию
R — это 0,7. Таим образом, при наложении стпи на ритерий F,
равный 0,5, мы пришли выбор варианта два.
Совершенно анало ично можно наложить стп и на вто-
рой по важности ритерий. Мы не бдем это о делать.
Вывод: при использовании принципа последовательной с-
тпи выбирается второй вариант.
FRV
1 — — —
20,80,70,5
310,61
Крит.
№ вар.
226
и та из этих смм, оторая оажется масимальной, соответствет
лчшем вариант.
Воспольземся этими соотношениями:
1-й вариант — 0,4 + 1 + 0,25 = 1,65;
2-й вариант — 0,8 + 0,7 + 0,5 = 2,0;
3-й вариант — 1 + 0,6 + 1 = 2,6 (max).
Просматривая значения полченных смм, выбираем маси-
мальное значение, это и бдет наилчшим вариантом.
Вывод: если задаться принципом абсолютной стпи, то
предпочтение следет отдать вариант три.
Принцип относительной стпи.
Формально он записывается с помощью следюще о соотно-
шения:
= F = { |
l },
де x
j
= , x
i
= есть относительные значения приращения
лоальных ритериев.
В аждом столбце находится масимальное значение лоаль-
но о ритерия. После это о необходимо перейти новой таблице,
поделив все числа в столбцах предыдщей таблицы на масималь-
ное значение в аждом столбце. Далее, с этой новой таблицей вы-
полняются те же процедры, что и в принципе абсолютной стп-
и. Можно поазать, что при использовании это о омпромисса
оптимальном вариант соответствет модель масимизации произ-
ведения лоальных ритериев. Формально:
= F = → max.
Или, для слчая трех ритериев: для аждой строчи вычис-
ляется произведение:
f
11
· f
12
· f
13
,
f
21
· f
22
· f
23
,
f
31
· f
32
· f
33
,
и среди этих произведений ищется масимм — это и бдет лч-
ший вариант по данном омпромисс.
Использя эти соотношения, полчим:
1-й вариант — 0,4 · 1 · 0,25 = 0,1;
2-й вариант — 0,8 · 0,7 · 0,5 = 0,28;
3-й вариант — 1 · 0,6 · 1 = 0,6 (max).
F
opt
F ° ω
F
k
F x
j
j
J
+()
∈
∑
x
i
j
I
–()
∈
∑
f
j
∆
f
j max
------------
f
i
∆
f
i max
------------
F opt
F ° ω
F
k
f
q
q 1=
k
∏
227
Вывод: если в ачестве схемы омпромисса выбрать принцип от-
носительной стпи,то предпочтение следет отдать вариант три.
2.3. Принцип выделения одноо оптимизиремоо ритерия.
При выборе модели плоттера лавным ритерием является
формат печатаемых материалов F, поэтом, просматривая первый
столбец в табл. 6.4, необходимо найти масимальное значение
соответствюще о ритерия:
0,4; 0,8; 1 (mах).
Масимальное значение соответствет третьем вариант, это
и бдет оптимальным вариантом.
Вывод: оптимальным вариантом является третий при использо-
вании принципа выделения одно о оптимизиремо о ритерия.
2.4. Принцип последовательной стпи.
Псть важность лоальных ритериев соответствет их после-
довательной записи в табл. 6.3, т. е. самым важным параметром
является форма, менее важным — разрешение, и наименее важ-
ным — объём памяти. Просматриваем первый столбец табл. 6.4 и
выбираем вариант, в отором F дости ает масимма:
0,4; 0,8; 1 (max).
Псть теперь мы со ласны наложить «стп» на ритерий F, и
псть эта «стпа» бдет равна ∆F = 0,5; то да имеем F
1, max
– ∆f
1
=
= 1 – 0,5 = 0,5; таим образом мы допсаем рассмотрению все
варианты, в оторых F не хже, чем 0,5. От табл. 6.4 переходим
табл. 6.5, де отображено это словие.
Таблица 6.5
Из рассмотрения ислючается первый вариант.
Теперь в табл.6.5 выбираем наилчший вариант по ритерию
R — это 0,7. Таим образом, при наложении стпи на ритерий F,
равный 0,5, мы пришли выбор варианта два.
Совершенно анало ично можно наложить стп и на вто-
рой по важности ритерий. Мы не бдем это о делать.
Вывод: при использовании принципа последовательной с-
тпи выбирается второй вариант.
FRV
1 — — —
20,80,70,5
310,61
Крит.
№ вар.
228
3. Выбор наилчшео варианта с четом приоритета лоальных
ритериев.
Псть приоритет ритериев задан следющим ветором
= (1, 2, 4). Переходим весовом ветор:
A = λ
1
λ
2
λ
3
+ λ
2
λ
3
+ λ
3
= 8 + 8 + 4 = 20;
α
1
= = = 0,4;
α
2
= = = 0,4;
α
3
= = = 0,2.
Имеем:
= (α
1
, α
2
, α
3
) = (0,4; 0,4; 0,2).
И от табл. 6.4 переходим табл. 6.6, в оторю подставляем
вместо f
i
→ α
i
f
i
.
Таблица 6.6
Теперь воспольземся известными схемами омпромисса.
3.1. Принцип равномерности.
Принцип равенства.
Слчай, о да все лоальные ритерии равны межд собой,
отстствет, поэтом эта модифиация применена быть не может.
Принцип вазиравенства.
Выбираем вариант, оторо о лоальные ритерии в маси-
мальной степени равны межд собой.
Вывод: по принцип вазиравенства предпочтение следет
отдать втором вариант.
Принцип масимина.
Рассматривая табл.6.6 построчно, в аждой строе выделяем
минимальное значение лоально о ритерия:
1-я строа — 0,1; 2-я строа — 0,2 (max); 3-я строа — 0,12.
Просматривая эти числа, среди них находим масимальное
значение, оно соответствет вариант два.
FRV
10,160,40,1
2 0,32 0,28 0,2
3 0,2 0,12 0,2
λ
λ
1
λ
2
λ
3
A
----------------- -
8
20
----- -
λ
2
λ
3
A
-----------
8
20
----- -
λ
3
A
-----
4
20
----- -
α
Крит.
№ вар.
229
Вывод: если воспользоваться принципом масимина, то
предпочтение следет отдать вариант два.
3.2. Принцип справедливой стпи.
Принцип абсолютной стпи.
Воспольземся здесь и ниже материалом, изложенным в пер-
вой части задачи.
1-й вариант — 0,16 + 0,4 + 0,1 = 0,66;
2-й вариант — 0,32 + 0,28 + 0,2 = 0,8; (max);
3-й вариант — 0,2 + 0,12 + 0,2 = 0,52.
Просматривая значения полченных смм, выбираем маси-
мальное значение, это и бдет наилчшим вариантом.
Вывод: если задаться принципом абсолютной стпи, то
предпочтение следет отдать вариант два.
Принцип относительной стпи.
1-й вариант — 0,16 · 0,4 · 0,1 = 0,0064;
2-й вариант — 0,32 · 0,28 · 0,2 = 0,01792; (max);
3-й вариант — 0,2 · 0,12 · 0,2 = 0,0048.
Просматривая полченные значения, выбираем масималь-
ное значение, это и бдет наилчшим вариантом.
Вывод: если в ачестве принципа выбрать принцип относи-
тельной стпи, то предпочтение следет отдать вариант два.
3.3. Принцип выделения одноо оптимизиремоо ритерия.
При выборе модели плоттера лавным ритерием является
формат печатаемых материалов F, поэтом, просматривая первый
столбец в табл.6.6, необходимо найти масимальное значение:
0,16; 0,32 (max); 0,2.
Масимальное значение соответствет втором вариант, это
и бдет оптимальным вариантом.
Вывод: оптимальным вариантом является второй при использо-
вании принципа выделения одно о оптимизиремо о ритерия.
3.4. Принцип последовательной стпи.
Псть важность лоальных ритериев соответствет их после-
довательной записи в табл.6.6, т.е. важнейшим параметром явля-
ется форма, менее важным — разрешение, и наименее важным —
объём памяти. Просматриваем первый столбец табл. 6.6 и выби-
раем вариант, в отором F дости ает масимма:
0,16; 0,32; (max); 0,2.
Псть теперь мы со ласны наложить «стп» на ритерий F, и
псть эта «стпа» бдет равна ∆F = 0,15, то да имеем F
1, max
– ∆f
1
=
= 0,32 – 0,15 = 0,17, таим образом, мы допсаем рассмотре-
нию все варианты, в оторых F не хже, чем 0,17. От табл. 6.6 пе-
реходим табл. 6.7, де отображено это словие:
228
3. Выбор наилчшео варианта с четом приоритета лоальных
ритериев.
Псть приоритет ритериев задан следющим ветором
= (1, 2, 4). Переходим весовом ветор:
A = λ
1
λ
2
λ
3
+ λ
2
λ
3
+ λ
3
= 8 + 8 + 4 = 20;
α
1
= = = 0,4;
α
2
= = = 0,4;
α
3
= = = 0,2.
Имеем:
= (α
1
, α
2
, α
3
) = (0,4; 0,4; 0,2).
И от табл. 6.4 переходим табл. 6.6, в оторю подставляем
вместо f
i
→ α
i
f
i
.
Таблица 6.6
Теперь воспольземся известными схемами омпромисса.
3.1. Принцип равномерности.
Принцип равенства.
Слчай, о да все лоальные ритерии равны межд собой,
отстствет, поэтом эта модифиация применена быть не может.
Принцип вазиравенства.
Выбираем вариант, оторо о лоальные ритерии в маси-
мальной степени равны межд собой.
Вывод: по принцип вазиравенства предпочтение следет
отдать втором вариант.
Принцип масимина.
Рассматривая табл.6.6 построчно, в аждой строе выделяем
минимальное значение лоально о ритерия:
1-я строа — 0,1; 2-я строа — 0,2 (max); 3-я строа — 0,12.
Просматривая эти числа, среди них находим масимальное
значение, оно соответствет вариант два.
FRV
10,160,40,1
2 0,32 0,28 0,2
3 0,2 0,12 0,2
λ
λ
1
λ
2
λ
3
A
----------------- -
8
20
----- -
λ
2
λ
3
A
-----------
8
20
----- -
λ
3
A
-----
4
20
----- -
α
Крит.
№ вар.
229
Вывод: если воспользоваться принципом масимина, то
предпочтение следет отдать вариант два.
3.2. Принцип справедливой стпи.
Принцип абсолютной стпи.
Воспольземся здесь и ниже материалом, изложенным в пер-
вой части задачи.
1-й вариант — 0,16 + 0,4 + 0,1 = 0,66;
2-й вариант — 0,32 + 0,28 + 0,2 = 0,8; (max);
3-й вариант — 0,2 + 0,12 + 0,2 = 0,52.
Просматривая значения полченных смм, выбираем маси-
мальное значение, это и бдет наилчшим вариантом.
Вывод: если задаться принципом абсолютной стпи, то
предпочтение следет отдать вариант два.
Принцип относительной стпи.
1-й вариант — 0,16 · 0,4 · 0,1 = 0,0064;
2-й вариант — 0,32 · 0,28 · 0,2 = 0,01792; (max);
3-й вариант — 0,2 · 0,12 · 0,2 = 0,0048.
Просматривая полченные значения, выбираем масималь-
ное значение, это и бдет наилчшим вариантом.
Вывод: если в ачестве принципа выбрать принцип относи-
тельной стпи, то предпочтение следет отдать вариант два.
3.3. Принцип выделения одноо оптимизиремоо ритерия.
При выборе модели плоттера лавным ритерием является
формат печатаемых материалов F, поэтом, просматривая первый
столбец в табл.6.6, необходимо найти масимальное значение:
0,16; 0,32 (max); 0,2.
Масимальное значение соответствет втором вариант, это
и бдет оптимальным вариантом.
Вывод: оптимальным вариантом является второй при использо-
вании принципа выделения одно о оптимизиремо о ритерия.
3.4. Принцип последовательной стпи.
Псть важность лоальных ритериев соответствет их после-
довательной записи в табл.6.6, т.е. важнейшим параметром явля-
ется форма, менее важным — разрешение, и наименее важным —
объём памяти. Просматриваем первый столбец табл. 6.6 и выби-
раем вариант, в отором F дости ает масимма:
0,16; 0,32; (max); 0,2.
Псть теперь мы со ласны наложить «стп» на ритерий F, и
псть эта «стпа» бдет равна ∆F = 0,15, то да имеем F
1, max
– ∆f
1
=
= 0,32 – 0,15 = 0,17, таим образом, мы допсаем рассмотре-
нию все варианты, в оторых F не хже, чем 0,17. От табл. 6.6 пе-
реходим табл. 6.7, де отображено это словие:

230
Таблица 6.7
Из рассмотрения ислючается первый вариант. Теперь в табл. 6.7
выбираем наилчший вариант по ритерию R, это 0,28. Таим об-
разом, при наложении стпи на ритерий F, равный 0,17, мы
пришли выбор второ о варианта.
Вывод: при использовании принципа последовательной с-
тпи выбирается второй вариант.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Рассмотрите основные словия, в оторых осществляется выбор
решения.
2. Перечислите основные рппы ораничивающих фаторов.
3. Что таое внешние и внтренние параметры?
4. Рассмотрите математичесю модель оптимальноо проетирования.
5. Рассажите, а реализется процесс принятия решений.
6. Сформлирйте общю постанов задачи принятия решений.
7. Приведите лассифиацию задач принятия решений.
8. В чем сщность одноритериальной задачи принятия решений?
9. Ка мот приниматься решения в словиях риса?
10. В чем отличия решений в словиях риса и в словиях неопределен-
ности?
11. Рассмотрите основные ритерии оптимальности выбора решений в
словиях неопределенности.
12. В чем сщность мнооритериальной задачи принятия решений?
13. Что представляет собой принцип равномерности?
14. В чем залючается принцип справедливой стпи?
15. В чем отличия принципа абсолютной стпи от принципа относи-
тельной стпи?
16. Поясните принцип выделения одноо оптимизиремоо ритерия.
17. Что представляет собой принцип последовательной стпи?
18. Что таое сверта лоальных ритериев?
19. Рассмотрите способы нормализации лоальных ритериев.
20. Рассмотрите способы задания и чета приоритета лоальных ритериев.
21. Что представляет собой ряд приоритета?
22. Что таое ветор приоритета? Ка задается весовой ветор?
23. Каим образом обычно оличественно задается приоритет ритериев?
24. Чем отличаются др от дра «жестий» и «ибий» приоритеты?
FRV
1 ———
2 0,32 0,28 0,2
3 0,2 0,12 0,2
Крит.
№ вар.
231
Раздел 2
ПРИКЛАДНЫЕ ВОПРОСЫ
АВТОМАТИЗИРОВАННОГО УПРАВЛЕНИЯ
Глава 7
ВИДЫ АВТОМАТИЗИРОВАННОГО
УПРАВЛЕНИЯ
Всяое правление предпола ает наличие объета правления
и правляюще о ор ана. Объеты правления чрезвычайно раз-
нообразны: предприятие, сложная техноло ичесая станова,
отрасль народно о хозяйства, живой ор анизм или е о часть,
чебное заведение, ород, область, респблиа. Управление пред-
ставляет собой сложный информационный процесс. Желатель-
но, чтобы правление осществлялось наилчшим образом, было
оптимальным.
В этой лаве рассматриваются различные виды правления:
централизованное, децентрализованное и иерархичесое. Таже
анализирются типовые ор анизационные стртры правления
производством.
Та а в онтре правления сложной системы обязательно
наличие человеа (т. е. сложная система все да является эр ати-
чесой, или человео-машинной системой), то на человеа воз-
ла ается часть фнций правления, причем наиболее ответс-
твенных. Ибо тольо челове способен честь при правлении
системой таие неформализемые поа фаторы, а социаль-
ные, психоло ичесие, моральные и физиоло ичесие.
7.1. Централизованное и децентрализованное
правление
Централизованный вид правления предпола ает реализацию
всех процессов правления объетами в едином центральном ор-
ане правления. Этот ор ан собирает информацию о состоянии
всех объетов правления, осществляет ее обработ и аждом
объет правления выдает свою собственню правляющю о-
манд (рис. 7.1).Управляющий ор ан воздействет на объет п-
равления посредством выдачи оманд. Эт информацию называ-
ют распорядительной. Посоль ор ан правления не безразлично
