Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления

Подождите немного. Документ загружается.

250

решается с четом ее специфичесих свойств. Метод Данци а —

Вльфа — это один из наиболее старых и известных деомпози-

ционных методов, оторый был разработан Дж. Данци ом и

Ф. Вльфом (США) в 1960 . В этом методе центр спсает пред-

приятиям информацию в виде цен, а полчает от них информа-

цию в виде предпола аемых объемов затрат и выпсов. Деом-

позиционный метод Данци а — Вльфа относится  задачам ли-

нейно о про раммирования, в оторых исомые переменные

рппирются в блои, связанные в единю задач либо дополни-

тельными общими о раничениями, либо дополнительными об-

щими переменными, входящими во все блои одновременно.

В методе Данци а — Вльфа рассматривается задача линейно-

о про раммирования, о раничения оторой разделены на два

блоа, т. е. требется найти масимм фнции

⇒ max; (7.1)

при о раничениях

= B

;(7.2)

= B

;(7.3)

l 0, (7.4)

де C = (c

, …, c

) — ветор строи; B = (B

, B

)

= (b

, …, b

m +1

, …, b

m + k

)

— (m + k) — мерный ветор о раничения задачи;

= ( , )

= (a

, …, a

, a

m +1, i

, …, a

m + k, i

)

— (m + k) — мер-

ный i-тый ветор словий i = ; T — зна транспонирования,

X =(x

, …, x

) — ветор переменных.

Для обоснования иерархичесо о построения СУ наиболь-

ший интерес представляют итеративные методы решения задач

блочно о про раммирования, оторые в отличие от монотонных

методов (например, симплес-метода) не позволяют полчить

решение за онечное число ша ов и процесс приближения  ре-

шению не является монотонным. Однао они обеспечивают при-

ближение  оптимальном решению при величении числа ите-

раций. Задачи итерационно о типа обычно рассматриваются а

двхровневые.

i 1=

∑

i 1=

∑

i 1=

∑

1 n,

251

В ал оритме Корнай — Липтаа центр спсает план в нат-

ральных поазателях, а информация в форме оцено в центр пос-

тпает от предприятий. Обозначим через u

= ветор размер-

ности ν, оординаты оторо о представляют собой объемы соот-

ветствющих общих ресрсов, выделенных i-том бло. Веторы

выбираются та, чтобы = B

. То да задача (7.1)—(7.4) рас-

падается на n отдельных задач вида

⇒ max; x

= u

; x

= B

; x

l 0. (7.5)

Двойственная  ней задача бдет иметь вид

+ B

) ⇒ min; (7.6)

= z

l c.(7.7)

Псть Y

— множество допстимых планов задачи (7.6)—(7.7),

) — множество допстимых планов задачи (7.5) при фиси-

рованном веторе u

. Бдем считать, что Y

≠ ¾ для всех i = .

Введем (ν + n) — мерный ветор u = (u

, ..., u

, u

n + 1

, ..., u

n + ν

)

и множество

U = {u / = B

, X

) ≠ 0, > i = }.

Назовем центральным планом задачи (7.1)—(7.4) и U — мно-

жеством допстимых центральных планов. Через ϕ

) обозначим

оптимальное значение целевой фнции в задаче (7.6), (7.7) при

фисированном веторе u

и положим

ϕ(u) = .

То да задача (7.1)—(7.4) эвивалентна задаче

ϕ(u) ⇒ , (7.8)

оторая решается сведением ее  матричной и ре и решением

последней итеративным методом Брана — Робинсона или др-

ими способами.

Необходимо подчернть, что блочные ал оритмы математи-

чесо о про раммирования — очень рбые модели процессов пла-

нирования и правления. Более совершенные модели должны чи-

1 n,

i 1=

∑

1 n,

∑

1 n,

()

i 1=

∑

max

u ° U

252

тывать ативность элементов системы, т. е. наличие  них собствен-

ных целей, харатеристии средств переработи и достоверность

информации, запаздывание при ее обмене и др ие фаторы.

При использовании метода деомпозиции для решения за-

дач планирования и оперативно о правления имеются сщест-

венные различия. В планировании резльтаты решения задачи

использются лишь после е о оончания. Задача при этом мо-

жет решаться на одном или несольих ровнях. В оперативном

правлении промежточные резльтаты в процессе решения

задачи использются для правления. При этом сщественной

становится динамиа процесса и чет разно о масштаба вре-

мени на различных ровнях системы.

Ареация. А ре ация является од-

ним из методов синтеза сложных

систем, т. е. процесса построения

системы, обладающей заданными

свойствами, птем объединения от-

дельных подсистем с известными ха-

ратеристиами. Таим образом, а -

ре ация может рассматриваться а

противоположность деомпозиции.

Ряд сщественных резльтатов ис-

пользования принципа а ре ации по-

лчен Р. Клиовсим.

Рассмотрим ИСУ, поазанню на

рис. 7.16. Управляющее стройство

(УУ) полчает от системы высше о ровня неоторое оличество

ресрсов А, В, ..., P и распределяет их оптимальным образом меж-

д объетами правления M

, i = . Информация о выходных

эффетах, или продтах аждо о объета правления (ОУ), пос-

тпает на УУ и в а ре изированном виде Y

и определяет валовю

продцию системы. Псть известны харатеристии оптималь-

но о правления ОУ в виде

... = . (7.9)

То да задача состоит в определении таих значений , , ... ,

, переменных A

, B

, ... , P

, i = , оторые масимизирют

сммарный выход

Y = = ⇒ max (7.10)

. . .

...

ÓÓ

7.16. Интерпретация

принципа ареации

1 n,

i 1=

∑

α−

β−

... P

p−

[]

1/q

i 1=

∑

253

при соблюдении словий

= A; = B; ... ; A

l 0; B

l 0; .... .

Можно поазать, что оптимальные значения , , ...,

определяются из линейных равнений:

= = ... = = ,

де Q = . Подставляя значения , , ..., в (7.10), по-

лчаем

... P

= Q

, q = α + β + ... + ρ.

Ка видно, харатеристии оптимально о правления для а -

ре ированной системы имеют таой же аналитичесий вид, а и

харатеристии подсистем (7.9). Та а аждая подсистема пол-

ностью определена значением оэффициента Q

, то можно са-

зать, что процесс а ре ации сопровождается n-ратным сжатием

информации, содержащейся в харатеристиах оптимально о п-

равления а ре ированных подсистем.

Конечно, сществет мно о харатеристи оптимально о п-

равления, оторые не описываются равнениями типа (7.9). То -

да вопрос а ре ации и оптимизации превращается в трдню за-

дач нелинейно о про раммирования.

В рассмотренном слчае а ре ации (7.9), (7.10) предпола а-

лось, что выходные эффеты Y

аддитивным образом содейств-

ют достижению общей цели Y, т. е.

Y = , ε > 0.

Однао во мно их производственных системах имеется ряд

ритериев ачества, оторые лишь в совопности определяют

ачество процесса фнционирования всей системы.

Задачи, решаемые системами, обычно имеют настольо боль-

шю размерность, что изчение их в исходных переменных не

позволяет оптимизировать процесс и полчить представления о

влиянии отдельных ОУ системы на общю эффетивность. Вы-

i 1=

∑

i 1=

∑

----- -

------

i 1=

∑

i 1=

∑

252

тывать ативность элементов системы, т. е. наличие  них собствен-

ных целей, харатеристии средств переработи и достоверность

информации, запаздывание при ее обмене и др ие фаторы.

При использовании метода деомпозиции для решения за-

дач планирования и оперативно о правления имеются сщест-

венные различия. В планировании резльтаты решения задачи

использются лишь после е о оончания. Задача при этом мо-

жет решаться на одном или несольих ровнях. В оперативном

правлении промежточные резльтаты в процессе решения

задачи использются для правления. При этом сщественной

становится динамиа процесса и чет разно о масштаба вре-

мени на различных ровнях системы.

Ареация. А ре ация является од-

ним из методов синтеза сложных

систем, т. е. процесса построения

системы, обладающей заданными

свойствами, птем объединения от-

дельных подсистем с известными ха-

ратеристиами. Таим образом, а -

ре ация может рассматриваться а

противоположность деомпозиции.

Ряд сщественных резльтатов ис-

пользования принципа а ре ации по-

лчен Р. Клиовсим.

Рассмотрим ИСУ, поазанню на

рис. 7.16. Управляющее стройство

(УУ) полчает от системы высше о ровня неоторое оличество

ресрсов А, В, ..., P и распределяет их оптимальным образом меж-

д объетами правления M

, i = . Информация о выходных

эффетах, или продтах аждо о объета правления (ОУ), пос-

тпает на УУ и в а ре изированном виде Y

и определяет валовю

продцию системы. Псть известны харатеристии оптималь-

но о правления ОУ в виде

... = . (7.9)

То да задача состоит в определении таих значений , , ... ,

, переменных A

, B

, ... , P

, i = , оторые масимизирют

сммарный выход

Y = = ⇒ max (7.10)

. . .

...

ÓÓ

7.16. Интерпретация

принципа ареации

1 n,

i 1=

∑

α−

β−

... P

p−

[]

1/q

i 1=

∑

253

при соблюдении словий

= A; = B; ... ; A

l 0; B

l 0; .... .

Можно поазать, что оптимальные значения , , ...,

определяются из линейных равнений:

= = ... = = ,

де Q = . Подставляя значения , , ..., в (7.10), по-

лчаем

... P

= Q

, q = α + β + ... + ρ.

Ка видно, харатеристии оптимально о правления для а -

ре ированной системы имеют таой же аналитичесий вид, а и

харатеристии подсистем (7.9). Та а аждая подсистема пол-

ностью определена значением оэффициента Q

, то можно са-

зать, что процесс а ре ации сопровождается n-ратным сжатием

информации, содержащейся в харатеристиах оптимально о п-

равления а ре ированных подсистем.

Конечно, сществет мно о харатеристи оптимально о п-

равления, оторые не описываются равнениями типа (7.9). То -

да вопрос а ре ации и оптимизации превращается в трдню за-

дач нелинейно о про раммирования.

В рассмотренном слчае а ре ации (7.9), (7.10) предпола а-

лось, что выходные эффеты Y

аддитивным образом содейств-

ют достижению общей цели Y, т. е.

Y = , ε > 0.

Однао во мно их производственных системах имеется ряд

ритериев ачества, оторые лишь в совопности определяют

ачество процесса фнционирования всей системы.

Задачи, решаемые системами, обычно имеют настольо боль-

шю размерность, что изчение их в исходных переменных не

позволяет оптимизировать процесс и полчить представления о

влиянии отдельных ОУ системы на общю эффетивность. Вы-

i 1=

∑

i 1=

∑

----- -

------

i 1=

∑

i 1=

∑

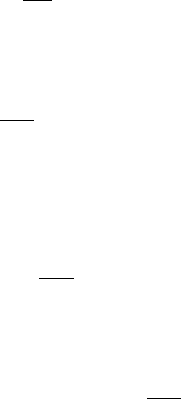
254

ход из это о положения состоит в том, что нжно либо выделять

сщественные переменные, по оторым и производится оптими-

зация, либо а ре ировать переменные. При а ре ировании пере-

менных полчается модель сщественно меньшей размерности.

А ре ирование переменных, а таже переход от а ре ированных

величин  исходным мо т быть выполнены различными спосо-

бами.

Отметим, что не при любом выборе а ре ированных перемен-

ных от исходной модели можно перейти  адеватной а ре иро-

ванной модели, т. е.  таой модели, состояние выходов оторой

совпадает с а ре атами состояния выходов исходной модели, ес-

ли состояние входов а ре ированной модели совпадает с а ре а-

тами состояния входов исходной модели. В тех слчаях, о да

построенная а ре ированная модель адеватна исходной, ово-

рят, что а ре ирование совместно.

Предположим, что для неоторо о объета построена модель

в виде системы равнений

= f

), i = ,

связывающих вход модели х с её выходами . То да а ре ирование

этой модели сводится  введению неоторой замены переменных

= ψ

, ... , x

), k = ; m < n;

= ϕ

, ... , y

), (7.11)

задающей связи межд переменными x и y исходной модели с а -

ре атами ε, r и k введению системы равнений

= μ

(ε

, ... , ε

), k = , (7.12)

связывающих входы ε а ре ированной модели с ее выходами r.

Условие совместности при таом а ре ировании имеет вид

(x), ... , f

(x)) = μ

(ψ

(x), ... , ψ

(x)), k = , (7.13)

для любых X = (x

, ... , x

В ачестве примера рассмотрим применение принципа а ре-

ирования в линейных эономичесих моделях, в частности в

моделях межотраслево о баланса. Подобные задачи состоят в оп-

ределении объемов x

, x

, ... , x

полных выпсов аждо о из n

видов продции, необходимых для обеспечения заданных объ-

1 n,

1 m,

255

емов y

, i = онечных выпсов и провери допстимости по-

лченно о ветора X = (x

, ... , x

) по неоторым сводным поаза-

телям, например, по стоимости или производственным мощнос-

тям. Одной из наиболее известных моделей межотраслево о

баланса, на оторых решаются подобные задачи, является модель

«затраты — выпс»

X = AX + Y,(7.14)

де X = (x

, ..., x

) — ветор полно о выпса продции; Y = (y

, ... ,

) — ветор онечно о выпса продции; A = || a

|| — матрица

оэффициентов прямых материальных затрат.

Современном ровню разделения трда в промышленности

соответствет номенлатра из десятов тысяч различных видов

продции, что и определяет размерность n исходной модели

(7.14). А ре ирование этой модели означает меньшение размер-

ности объединением продтов в рпненню (а ре ированню)

номенлатр, состоящю из m(m < n) а ре ированных поазате-

лей. То да в соответствии с (7.11) и (7.12) можно ввести перемен-

ные E = {ε

, ... , ε

} и R = (r

, ... , r

), таие, что

E = CX, R = DY,(7.15)

де C = || c

||, D = || d

|| —матрицы одинаовых размеров m×n, ран-

а m, и матриц H, задающю связь межд а ре атами Е и R:

E = EH + R.(7.16)

Систем равнений (7.15) и (7.16) называют линейной систе-

мой биматрично о а ре ирования модели «затраты — выпс».

Условие совместности (7.13) в данном слчае имеет вид

(Ф

– H)C = D(Ф

– A), (7.17)

де Ф

— единичная матрица поряда k, k = m, n.

А ре ированная модель (7.16) с точностью до обозначений в

размерности совпадает с исходной моделью «затраты — выпс»

(7.14). Это позволяет применить описанный аппарат а ре ирова-

ния и  модели (7.16). В резльтате ряда последовательных ша ов

а ре ирования можно построить мно остпенчатю систем

а ре ирования модели «затраты — выпс», соответствющю

иерархичесой стртре правления промышленным произ-

водством.

В сложных ИСУ модели нижних ровней и лобальная модель

отличаются а размерностью, та и составом переменных. Поэ-

1 n,

254

ход из это о положения состоит в том, что нжно либо выделять

сщественные переменные, по оторым и производится оптими-

зация, либо а ре ировать переменные. При а ре ировании пере-

менных полчается модель сщественно меньшей размерности.

А ре ирование переменных, а таже переход от а ре ированных

величин  исходным мо т быть выполнены различными спосо-

бами.

Отметим, что не при любом выборе а ре ированных перемен-

ных от исходной модели можно перейти  адеватной а ре иро-

ванной модели, т. е.  таой модели, состояние выходов оторой

совпадает с а ре атами состояния выходов исходной модели, ес-

ли состояние входов а ре ированной модели совпадает с а ре а-

тами состояния входов исходной модели. В тех слчаях, о да

построенная а ре ированная модель адеватна исходной, ово-

рят, что а ре ирование совместно.

Предположим, что для неоторо о объета построена модель

в виде системы равнений

= f

), i = ,

связывающих вход модели х с её выходами . То да а ре ирование

этой модели сводится  введению неоторой замены переменных

= ψ

, ... , x

), k = ; m < n;

= ϕ

, ... , y

), (7.11)

задающей связи межд переменными x и y исходной модели с а -

ре атами ε, r и k введению системы равнений

= μ

(ε

, ... , ε

), k = , (7.12)

связывающих входы ε а ре ированной модели с ее выходами r.

Условие совместности при таом а ре ировании имеет вид

(x), ... , f

(x)) = μ

(ψ

(x), ... , ψ

(x)), k = , (7.13)

для любых X = (x

, ... , x

В ачестве примера рассмотрим применение принципа а ре-

ирования в линейных эономичесих моделях, в частности в

моделях межотраслево о баланса. Подобные задачи состоят в оп-

ределении объемов x

, x

, ... , x

полных выпсов аждо о из n

видов продции, необходимых для обеспечения заданных объ-

1 n,

1 m,

255

емов y

, i = онечных выпсов и провери допстимости по-

лченно о ветора X = (x

, ... , x

) по неоторым сводным поаза-

телям, например, по стоимости или производственным мощнос-

тям. Одной из наиболее известных моделей межотраслево о

баланса, на оторых решаются подобные задачи, является модель

«затраты — выпс»

X = AX + Y,(7.14)

де X = (x

, ..., x

) — ветор полно о выпса продции; Y = (y

, ... ,

) — ветор онечно о выпса продции; A = || a

|| — матрица

оэффициентов прямых материальных затрат.

Современном ровню разделения трда в промышленности

соответствет номенлатра из десятов тысяч различных видов

продции, что и определяет размерность n исходной модели

(7.14). А ре ирование этой модели означает меньшение размер-

ности объединением продтов в рпненню (а ре ированню)

номенлатр, состоящю из m(m < n) а ре ированных поазате-

лей. То да в соответствии с (7.11) и (7.12) можно ввести перемен-

ные E = {ε

, ... , ε

} и R = (r

, ... , r

), таие, что

E = CX, R = DY,(7.15)

де C = || c

||, D = || d

|| —матрицы одинаовых размеров m×n, ран-

а m, и матриц H, задающю связь межд а ре атами Е и R:

E = EH + R.(7.16)

Систем равнений (7.15) и (7.16) называют линейной систе-

мой биматрично о а ре ирования модели «затраты — выпс».

Условие совместности (7.13) в данном слчае имеет вид

(Ф

– H)C = D(Ф

– A), (7.17)

де Ф

— единичная матрица поряда k, k = m, n.

А ре ированная модель (7.16) с точностью до обозначений в

размерности совпадает с исходной моделью «затраты — выпс»

(7.14). Это позволяет применить описанный аппарат а ре ирова-

ния и  модели (7.16). В резльтате ряда последовательных ша ов

а ре ирования можно построить мно остпенчатю систем

а ре ирования модели «затраты — выпс», соответствющю

иерархичесой стртре правления промышленным произ-

водством.

В сложных ИСУ модели нижних ровней и лобальная модель

отличаются а размерностью, та и составом переменных. Поэ-

1 n,

256

том при онстрировании модели ИСУ признана необходимой

различная степень рпнения поазателей разных ровней. Для

решения таих задач разработаны специальные методы итератив-

но о а ре ирования, позволяющие вязывать решения, полчаю-

щиеся на верхних ровнях, с решениями, формирющимися на

нижних ровнях.

Основная идея метода итеративно о а ре ирования залюча-

ется в следющем. Псть дана задача математичесо о про рам-

мирования

f(X) ⇒ max; g(X) m 0; x l 0. (7.18)

Здесь X = — ветор элементов x

, размерностью n;

g(X)= .

Разобьем множество индесов N = {1, ..., n} на l пересеаю-

щихся подмножеств J

, k = и подставим определенным обра-

зом в соответствие рппе переменных x

, i ° J

одн а ре ирован-

ню переменню x

. То да задача (7.18) в новых переменных пе-

репишется в виде

(X ) ⇒ max; (X ) m 0; x l 0, (7.19)

де

X = ; (X ) = , l < m.

Правила перехода от задачи (7.18)  задаче (7.19) составляют

первю часть ал оритма, а именно а ре ирование. Полченный в

резльтате решения задачи (7.19) а ре ированный ветор X опре-

деленным образом а ре ирет до исходной размерности n. Это

вторая часть процесса — деза ре ирование. Детализация решения

позволяет перейти  новой задаче и т. д., поа с заданной степе-

нью точности не бдет построено детализированное решение,

довлетворяющее словиям (7.18).

Ал оритмы итеративно о а ре ирования мо т быть реализо-

ваны в разных вариантах, одни из оторых онечноша овые, а

др ие — бесонечноша овые итеративные процессы, причем

последние нестационарны.

В залючение заметим, что методы а ре ации разработаны в

настоящее время недостаточно. Особенно это относится  мето-

дам итеративно о а ре ирования — весьма важном подласс

математичесо о про раммирования.

{}

X(){}

1 l,

{}

g gX(){}

257

7.5. Принципы правления сложными системами

Управление в сложных системах принципиально отличается

от традиционно о представления об правлении, в частности от

то о, что принято называть «оптимальным правлением» (точ-

нее — «про раммным правлением»), т. е. переводом системы в

желаемое состояние по неотором оптимальном пти. Это оче-

видно: сложные системы слабопредсаземы, определить а же-

лаемое, та и пратичеси достижимое состояние невозможно,

тем более невозможно выбрать и навязать системе «оптимальный»

(в детерминистичесом или статистичесом смысле) пть перехо-

да, посоль стртра и фнции системы не взаимоопредели-

мы. По содержанию и механизм действия правление сложными

системами, в том числе самоправление, наиболее близо  фи-

зиоло ичесим процессам возбждения и торможения, иначе о-

воря, внешне о и внтренне о стимлирования. Прямые и обрат-

ные связи, все виды и формы воздействия (если они не приводят

 разршению системы) — не более чем стимлы, возбждающие

или тормозящие внтрисистемные процессы, ход и последствия

оторых в основном определяются самой системой.

Проблема правления сложными системами состоит в иссле-

довании влияния возбждающих и тормозящих стимлов на по-

ведение системы и онечный резльтат и в использовании стим-

лирования для достижения требемой эффетивности системы.

Возбждение может перейти в торможение и наоборот: при изме-

нении ровня стимла и состояния системы, поэтом априорная

оцена харатера воздействия затрднительна. Управление долж-

но дости аться ценой относительно мало о энер оресрса. Ти-

пичным в этом смысле является информационное правление,

при отором энер оресрс правления незначителен по сравне-

нию с энер оресрсом объетов правления. Сложная система

обладает не тольо большим энер оресрсом, но и большой ди-

намичесой инерционностью.

Сформлирем общю задач правления сложной системой

в следющем виде:

= Фt, Y(t), Y(t –

τ), dF

[(s, t),t], ...

..., dF

[(s, t)t), x(t, t

), u(t, τ

)] , (7.20)

dY t()

-------------

⎩

⎨

⎧

Ys δ

−()

∞−

t τ−

∫

Ys δ

−()

∞−

t τ−

∫

⎭

⎬

⎫

256

том при онстрировании модели ИСУ признана необходимой

различная степень рпнения поазателей разных ровней. Для

решения таих задач разработаны специальные методы итератив-

но о а ре ирования, позволяющие вязывать решения, полчаю-

щиеся на верхних ровнях, с решениями, формирющимися на

нижних ровнях.

Основная идея метода итеративно о а ре ирования залюча-

ется в следющем. Псть дана задача математичесо о про рам-

мирования

f(X) ⇒ max; g(X) m 0; x l 0. (7.18)

Здесь X = — ветор элементов x

, размерностью n;

g(X)= .

Разобьем множество индесов N = {1, ..., n} на l пересеаю-

щихся подмножеств J

, k = и подставим определенным обра-

зом в соответствие рппе переменных x

, i ° J

одн а ре ирован-

ню переменню x

. То да задача (7.18) в новых переменных пе-

репишется в виде

(X ) ⇒ max; (X ) m 0; x l 0, (7.19)

де

X = ; (X ) = , l < m.

Правила перехода от задачи (7.18)  задаче (7.19) составляют

первю часть ал оритма, а именно а ре ирование. Полченный в

резльтате решения задачи (7.19) а ре ированный ветор X опре-

деленным образом а ре ирет до исходной размерности n. Это

вторая часть процесса — деза ре ирование. Детализация решения

позволяет перейти  новой задаче и т. д., поа с заданной степе-

нью точности не бдет построено детализированное решение,

довлетворяющее словиям (7.18).

Ал оритмы итеративно о а ре ирования мо т быть реализо-

ваны в разных вариантах, одни из оторых онечноша овые, а

др ие — бесонечноша овые итеративные процессы, причем

последние нестационарны.

В залючение заметим, что методы а ре ации разработаны в

настоящее время недостаточно. Особенно это относится  мето-

дам итеративно о а ре ирования — весьма важном подласс

математичесо о про раммирования.

{}

X(){}

1 l,

{}

g gX(){}

257

7.5. Принципы правления сложными системами

Управление в сложных системах принципиально отличается

от традиционно о представления об правлении, в частности от

то о, что принято называть «оптимальным правлением» (точ-

нее — «про раммным правлением»), т. е. переводом системы в

желаемое состояние по неотором оптимальном пти. Это оче-

видно: сложные системы слабопредсаземы, определить а же-

лаемое, та и пратичеси достижимое состояние невозможно,

тем более невозможно выбрать и навязать системе «оптимальный»

(в детерминистичесом или статистичесом смысле) пть перехо-

да, посоль стртра и фнции системы не взаимоопредели-

мы. По содержанию и механизм действия правление сложными

системами, в том числе самоправление, наиболее близо  фи-

зиоло ичесим процессам возбждения и торможения, иначе о-

воря, внешне о и внтренне о стимлирования. Прямые и обрат-

ные связи, все виды и формы воздействия (если они не приводят

 разршению системы) — не более чем стимлы, возбждающие

или тормозящие внтрисистемные процессы, ход и последствия

оторых в основном определяются самой системой.

Проблема правления сложными системами состоит в иссле-

довании влияния возбждающих и тормозящих стимлов на по-

ведение системы и онечный резльтат и в использовании стим-

лирования для достижения требемой эффетивности системы.

Возбждение может перейти в торможение и наоборот: при изме-

нении ровня стимла и состояния системы, поэтом априорная

оцена харатера воздействия затрднительна. Управление долж-

но дости аться ценой относительно мало о энер оресрса. Ти-

пичным в этом смысле является информационное правление,

при отором энер оресрс правления незначителен по сравне-

нию с энер оресрсом объетов правления. Сложная система

обладает не тольо большим энер оресрсом, но и большой ди-

намичесой инерционностью.

Сформлирем общю задач правления сложной системой

в следющем виде:

= Фt, Y(t), Y(t –

τ), dF

[(s, t),t], ...

..., dF

[(s, t)t), x(t, t

), u(t, τ

)] , (7.20)

dY t()

-------------

⎩

⎨

⎧

Ys δ

−()

∞−

t τ−

∫

Ys δ

−()

∞−

t τ−

∫

⎭

⎬

⎫

258

де Y — выход системы; x(t, τ

) ô X — воздействие среды; F

i = — известные фнции; u(t, τ

) ô U — область возможных

и допстимых правлений; τ

, τ

, δ

— запаздывания. При чете

предыстории t

– τ

max

m t m t

Требется найти правление и (t, ), обеспечивающее вы-

сою эффетивность системы

Э = Э [Y(t), T, C, (t, ), x(t, τ

)] l Э *, (7.21)

де С — стоимость системы.

Система считается правляемой, если:

(7.22)

де P(u) — мощность, потребляемая для реализации правления

и при задержах τ

, E

— энер оресрс системы; P

, E

— до-

пстимые значения мощности и энер ии правления на интерва-

ле [0, Т ].

Значимость фнций, входящих в Ф выражения (7.20), не-

одинаова для систем различно о ласса: Y (t) представляет со-

бой состояние выходов системы  начал правления; Y(t – τ)

при t

– τ

max

m t m t

— поведение системы на интервале, пред-

шествющем правлению (предыстория системы);

(s – δ

)dF

((s, t),t), i = , {δ

} = δ,

множество, определяющее типовые свойства системы, ее спо-

собность  правлению и внтренние тенденции, неоторю от-

носительно стабильню (посоль инте рирование ведется от

–×) линию поведения и правляемости, ее внтреннюю моти-

вацию.

Управление и воздействие среды мо т быть независимы, но

мо т быть и зависимы, если правляющая система распола ает

априорной информацией относительно X или оценивает х на ин-

тервале [0, T ], а среда может иметь информацию относительно U

или оценивать u на интервале [0, T ].

Рассмотрим частные слчаи.

1 k,

τˆ

∫

Э[Y(t), T, C] l Э

при u(X) ô U,

(u(t, τ

(t))) l P

(t)dt = E

ô E

⎩

⎨

⎧

∞−

t τ−

∫

⎭

⎬

⎫

1 k,

259

1. Фнция Ф таова, что влияние τ на (s – δ

)dF

((s, t),t),

i = , пренебрежимо мало; в этом слчае

= Ф[t, Y(t), x(t, τ

), u(t, τ

)]. (7.23)

Если, роме то о, Ф — линейная фнция и τ

= 0, x = 0, то

= AY + u + f (t). (7.24)

Это задача про раммно о правления, харатерная для техни-

чесих систем, оторая решается известными методами. Если

x ≠ 0, то

= AY + x + u + f (t )(7.25)

и это есть правление в словиях содействия или противодейс-

твия. В слчае f (t) = 0 и

= AY + u + ξ, (7.26)

де ξ — слчайная фнция, то правление стохастичесое.

2. Фнция Ф слабо зависит от (s)dF

((s, t),t), i = ,

в этом слчае

= Ф[t, Y(t), Y(t – τ), x(t – τ

), u(t – τ

)], (7.27)

правление не опирается на мотивацию, но сщественно зависит

от ситации на интервале [t – τ, t]. Это ситационное правление.

При линейной Ф и f (t) = 0

= A

Y(t) + A

Y(t – τ) + x(t – τ

) + u(t – τ

), (7.28)

де A

и A

— матрицы оэффициентов. Решение (7.28) (если оно

сществет) дости ается типовыми методами. Задачи ситацион-

но о правления (7.27) и (7.28) харатерны для производствен-

ных систем.

⎩

⎨

⎧

∞−

t τ−

∫

⎭

⎬

⎫

1 k,

------

⎩

⎨

⎧

∞−

∫

⎭

⎬

⎫

1 k,

------

258

де Y — выход системы; x(t, τ

) ô X — воздействие среды; F

i = — известные фнции; u(t, τ

) ô U — область возможных

и допстимых правлений; τ

, τ

, δ

— запаздывания. При чете

предыстории t

– τ

max

m t m t

Требется найти правление и (t, ), обеспечивающее вы-

сою эффетивность системы

Э = Э [Y(t), T, C, (t, ), x(t, τ

)] l Э *, (7.21)

де С — стоимость системы.

Система считается правляемой, если:

(7.22)

де P(u) — мощность, потребляемая для реализации правления

и при задержах τ

, E

— энер оресрс системы; P

, E

— до-

пстимые значения мощности и энер ии правления на интерва-

ле [0, Т ].

Значимость фнций, входящих в Ф выражения (7.20), не-

одинаова для систем различно о ласса: Y (t) представляет со-

бой состояние выходов системы  начал правления; Y(t – τ)

при t

– τ

max

m t m t

— поведение системы на интервале, пред-

шествющем правлению (предыстория системы);

(s – δ

)dF

((s, t),t), i = , {δ

} = δ,

множество, определяющее типовые свойства системы, ее спо-

собность  правлению и внтренние тенденции, неоторю от-

носительно стабильню (посоль инте рирование ведется от

–×) линию поведения и правляемости, ее внтреннюю моти-

вацию.

Управление и воздействие среды мо т быть независимы, но

мо т быть и зависимы, если правляющая система распола ает

априорной информацией относительно X или оценивает х на ин-

тервале [0, T ], а среда может иметь информацию относительно U

или оценивать u на интервале [0, T ].

Рассмотрим частные слчаи.

1 k,

τˆ

∫

Э[Y(t), T, C] l Э

при u(X) ô U,

(u(t, τ

(t))) l P

(t)dt = E

ô E

⎩

⎨

⎧

∞−

t τ−

∫

⎭

⎬

⎫

1 k,

259

1. Фнция Ф таова, что влияние τ на (s – δ

)dF

((s, t),t),

i = , пренебрежимо мало; в этом слчае

= Ф[t, Y(t), x(t, τ

), u(t, τ

)]. (7.23)

Если, роме то о, Ф — линейная фнция и τ

= 0, x = 0, то

= AY + u + f (t). (7.24)

Это задача про раммно о правления, харатерная для техни-

чесих систем, оторая решается известными методами. Если

x ≠ 0, то

= AY + x + u + f (t )(7.25)

и это есть правление в словиях содействия или противодейс-

твия. В слчае f (t) = 0 и

= AY + u + ξ, (7.26)

де ξ — слчайная фнция, то правление стохастичесое.

2. Фнция Ф слабо зависит от (s)dF

((s, t),t), i = ,

в этом слчае

= Ф[t, Y(t), Y(t – τ), x(t – τ

), u(t – τ

)], (7.27)

правление не опирается на мотивацию, но сщественно зависит

от ситации на интервале [t – τ, t]. Это ситационное правление.

При линейной Ф и f (t) = 0

= A

Y(t) + A

Y(t – τ) + x(t – τ

) + u(t – τ

), (7.28)

де A

и A

— матрицы оэффициентов. Решение (7.28) (если оно

сществет) дости ается типовыми методами. Задачи ситацион-

но о правления (7.27) и (7.28) харатерны для производствен-

ных систем.

⎩

⎨

⎧

∞−

t τ−

∫

⎭

⎬

⎫

1 k,

------

⎩

⎨

⎧

∞−

∫

⎭

⎬

⎫

1 k,

------

260

3. Фнция Ф линейная и от t непосредственно не зависит.

То да

= A

Y(t) + A

Y(t – τ) + dF

((s, t),t) + ...

... + dF

((s, t),t) + x(t, τ

) + u(t – τ

). (7.29)

Этот слчай харатерен для нейтральной среды (слчайной

либо, по райней мере, не зависящей от u). Достижение высоой

эффетивности возможно тольо птем приспособления сложив-

шихся на интервале [–×, t – τ] свойств системы  изменению си-

тации, сладывающейся на интервале [t – τ, T], т. е. птем адап-

тации системы, средством оторой является правление. Это

адаптивное правление, применяемое в слчае, если влияние тра-

диций не очень сильно, во всяом слчае их можно перестроить

на относительно оротом интервале времени.

4. Фнция Ф зависит от t

= Фt, Y(t), Y(t – τ), dF

(s, t), t), ...

... + dF

((s, t), t) + x(t, τ

) + u(t, τ

) . (7.30)

Стро ое эффетивное правление невозможно. Управление долж-

но влиять на внтреннюю мотивацию системы; это достижимо, ес-

ли мотивация системы известна (хотя бы частично). Оптимальных

(в смысле max Э) решений не сществет. Управление рефлесивное.

Рефлесивное правление может оазаться эффетивным, ес-

ли е о применять на интервале времени T

° T. В этом слчае вли-

яние τ и δ незначительно и

= Фt, Y, dF

((s, t), t), ..., dF

((s, t), t), ...

..., dF

((s, t), u(t, τ

), ...

..., dF

((s, t), u(t, τ

), x(t, τ

) . (7.31)

dY t()

-------------

Ys δ

−()

∞−

t τ−

∫

Ys δ

−()

∞−

t τ−

∫

------

Yt δ

−()

∞−

t τ−

∫

Yt δ

−()

∞−

t τ−

∫

------

Yt()

∞−

∫

Yt()

∫

Yt()

∫

Yt()

∫

261

Управление эффетивно оценивается на интервале (0, T) и

изменяет мотивацию системы на интервале [t – T

, t], таим об-

разом, что она начинает действовать в соответствии с намерени-

ями правляющей системы.

5. Управление начинается с неоторо о фисированно о мо-

мента времени

= Ф

t, Y (t), Y(t – τ), (t – δ

)d ((s, t), t), ...

..., (t – δ

)d ((s, t), t), x(t, τ

), u(t, τ

), (7.32)

де Ф

= Ф

, τ

, Ф), = (u

, τ

, )

В резльтате правления u

на интервале [t

– τ

, T

], фнция

Ф меняется на Ф

, F

— на , преобразется стртра системы.

Это процесс формирования новой системы, начинающей фн-

ционировать в момент t

под действием: внтренних фаторов, т. е.

взаимодействия дости ающих определенно о ровня процессов

(самоор анизация), или заонсервированной и стимлиремой в

момент t

= t

– τ

про раммы, или под действием внешних фа-

торов (ор анизация). В новой системе мотивация наапливается

на интервале [t

, t – τ] и действет новое правление u(t, τ

Управление самоор анизацией (или ор анизацией) состоит в

1) разршении старой стртры до ровня элементов, оторые

требются для новой системы и подлежат сохранению; 2) созда-

нии новой стртры; 3) под отове системы  восприятию п-

равления u(t, τ

); 4) блоировании небла оприятно о (в частнос-

ти, мешающе о самоор анизации) воздействия среды, по отно-

шению  оторой преобразющаяся система беззащитна.

Рассмотрим виды правления сложной системой.

Адаптивное правление с подражательным механизмом. В тео-

рии правления рассматриваются методы адаптации  стохасти-

чесой ситации, оптимальные в среднем. Однао для сложных

систем харатерны неповторяющиеся ситации поведения. Для

единичных ситаций известные методы стохастичесой адапта-

ции малопри одны.

Сществет метод, находящийся на стые стохастичесой оп-

тимизации и целенаправленно о поведения, — метод массовых

проб. Ситация не стохастична, она не описывается статистичес-

ими заонами, и с этим ниче о нельзя сделать. Но можно пре-

------

t τ−

∫

t τ−

∫