Медведев Г.А. Математические основы финансовой экономики. Часть 1
Подождите немного. Документ загружается.


222
()
∫
++
T
ssss
dsfqqr
0
2
<
∞
почти всюду. Часть в) утверждения следует из
получаемых по формуле Ито равенств
sssss
fqqr
−+=µ
2
и
σ
s
=
f
s
−
q
s
.
Следующее следствие утверждения 5.2 может служить первым
объяснением названия «нейтральная к риску вероятность», исполь-
зуемого для меры
Q
с плотностью
ρ =
.
2
1
exp
0
2
0
−
∫∫
T
u
T
uu
duqdBq
Следствие 5.3.
При выполнении предположений 5.11 процесс
r
t
является функцией дрейфа
Р
(
t
,
Т
) относительно нейтральной к риску
вероятностной мере
Q.
Доказательство. Теорема Гирсанова (см. Р. Липцер, А. Ширя-
ев, теорема 6.3) гарантирует, что процесс
∫
−=
u
suu
dsqBB
0
~
является
броуновским движением при вероятностной мере
Q
и выражение
dР
может быть записано согласно в) утверждения 5.2 как
dР
(
t
,
Т
) = (
µ
t
+ σ
t
q
t
)
Р
t
dt
+
σ
t
Р
t
(
dВ
t
−
q
t
dt
) =
r
t
Р
t
dt + σ
t
Р
t
t
Bd
~
.
Функционал (
q
s
)
0
≤
s
≤
T
может быть интерпретирован как
цена за
единицу риска
, измеряемого разностью между доходами облигации и
(локально свободным от риска) сберегательного счета.
Описание функции дрейфа в стохастических
дифференциалах
Рассмотрим проблему единственности. Из структуры мартинга-
лов по отношению к (
F
t
)
t
≤
Т
следует, что встречающиеся предсказуе-
мые процессы определяются с точностью до множеств меры нуль в
пространстве
[
0,
Т]
×
Ω
, оснащенном произведением мер
т
⊗
Р
,
т
−
мера Лебега на
[
0,
Т]
; поэтому единственность должна пониматься с
точностью до множеств
т
⊗
Р
меры нуль.
Единственность определения цены актива связана посредством
результатов § 1 с единственностью нейтральной к риску меры
Q
, а от-
сюда – с единственностью процесса (
q
s
)
0
≤
s
≤
T
в утверждении 5.1. По-
этому мы исследуем проблему того, как можно идентифицировать
процесс (
q
s
)
0
≤
s
≤
T
из (
Z
t
)
0
≤
t
≤
T
с помощью дифференциального выра-
жения утверждения 5.2. Следующая теорема, достаточно формальная
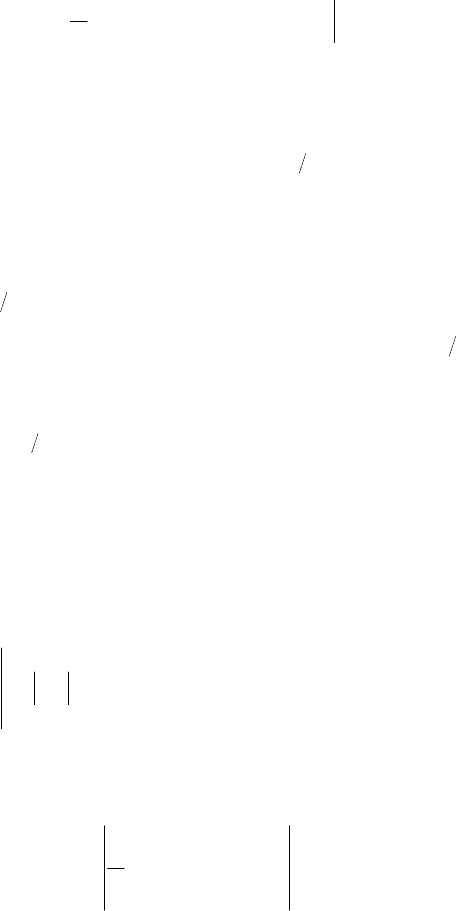
223
по характеру, расширяет известные условия, при которых коэффици-
ент дрейфа оказывается условным математическим ожиданием ставки
доходности.
Теорема 5.3.
Пусть (
Х
и
)
0
≤
и
≤
T
является непрерывным процессом
с дифференциалом Ито
dХ
и
= λ
и
dи + k
и
dВ
и
,
∫
+λ
T
uu
duk
0
2
|)|||( <
∞
почти всюду.
Тогда по мере
т
⊗
Р
на
[
0,
Т]
×
Ω
λ
и
=
()
(
)
uuhu
hN
FXXE
h
NN
τ∧τ∧+
→∞→
−
1
limlim
0
,
где почти всюду
τ
n
= inf
{и ||Х
и
|
≥
n}
∧ Т.
Доказательство. Из общей теории стохастических процессов
следует, что условные ожидания
Y
и
=
()
)|(
1
unu
FXE
n
τ∧+
могут быть
выбраны таким образом, чтобы (
Y
и
)
0
≤
и
≤
T
являлся непрерывным почти
всюду. Этот факт стандартный, но из-за сложности опишем
доказательство лишь в общих чертах.
Процесс
и
→
()
n
nu
X
τ∧+1
– измеримый и имеет измеримую проек-
цию
Y
и
. Последняя удовлетворяет равенству
Y
v
=
()
)|(
1
vnv
FXE
n
τ∧+
почти всюду для каждого момента остановки
v
, следовательно,
Y
и
=
()
)|(
1
unu
FXE
n
τ∧+
почти всюду,
и ≤
Т.
При предположении 5.8 семейство (
F
t
)
0
≤
t
≤
Т
квазинепрерывно
слева и, следовательно, достижимые и предсказуемые
σ
-алгебры сов-
падают. При заданном
ε
>
0 мы сначала выберем
N
так , чтобы
выполнялось неравенство (2 +
Т
)
Р[ν
N
<
Т]
< ε
для момента остановки
ν
N
= inf
TNdukNdut
t
u
t
u
∧
>>λ
∫∫
0
2
0
или ;
затем найдем
h
0
такое, чтобы математическое ожидание
Е
−
∫∫
∧+
],0[
)(
1
N
N
hu
u
us
ds
h
dm
ν
ν
λλ

224
было меньше
ε
для каждого
h
из
]
0,
h
0
[
. Это дает нам доказательство
теоремы в случае ограниченного процесса (
Х
и
)
0
≤
и
≤
T
. Обращаясь к об-
щему случаю, можно применить локализацию: дифференциал оста-
новленного процесса при
τ
N
(
N
u
X
τ∧
)
uuuuuu
dBkduXd
NNN
}{}{
)(
τ<τ<τ∧
+λ=
II
.
Отсюда следует, что по мере
т
⊗
Р
()
()
uuhu
h
FXXE
h
NN
ττ
∧∧+
→
−
1
lim
0
=
}{
N
uu
τ
λ
<
I
.
Переход к пределу
N
→ ∞
дает требуемый результат.
Результаты единственности
Теорема 5.3 позволяет воспользоваться средством изучения
единственности коэффициентов дрейфа и дисперсии в дифференци-
альном уравнении процесса цены облигации
Р
, так же как и единст-
венности процесса цены риска и нейтральной к риску вероятностной
меры. Во-первых, она непосредственно показывает, что по мере
т
⊗
Р
пределом (1/
h
)
Е[Р
(
и + h
,
Т
)
−
Р
(
и
,
Т
)
|
F
и
]
при
h →
0 является
µ
и
Р
(
и
,
Т
).
Далее следуют два других свойства.
Утверждение 5.3.
В предположениях 5.11 процессы (
µ
и
)
0
≤
и
≤
T
и
(
σ
и
)
0
≤
и
≤
T
(см. утверждение 5.2) однозначно определяются процесса-
ми (
r
и
)
0
≤
и
≤
T
и (
Р
(
и
,
Т
))
0
≤
и
≤
T
.
Доказательство. Поскольку
Р
не обращается в нуль, (
µ
и
)
0
≤
и
≤
T
регенерируется непосредственно. Так как
Р
(
t
,
Т
)
−
()
∫
µ
t
s
dsTsP
0
, явля -
ется локальным мартингалом, расширение р езультата представле-
ния (§ 5.2) на локальные мартингалы (см. Р. Липцер, А. Ширяев)
обеспечивает единственность (
σ
и
)
0
≤
и
≤
T
. Альтернативным доказатель-
ством является применение теоремы 5.1 к процессу
Р
(
t
,
Т
) ехр (
−В
t
2
),
чтобы получить по формуле Ито дрейф в виде
Р
(
t
,
Т
) ехр (
−
В
t
2
) (
µ
t
+
2
В
t
2
−
1
−
2
σ
t
В
t
).
Так как по предположениям 5.8 и 5.9
В
t
является регенерируе-
мым из процесса (
r
и
)
0
≤
и
≤
t
, знание процессов (
Р
(
и
,
Т
))
0
≤
и
≤
T
и (
r
и
)
0
≤
и
≤
T
дает возможность определить (
µ
и
)
0
≤
и
≤
T
и (
σ
и
)
0
≤
и
≤
T
.

225
Для процесса «цены риска» единственность вытекает из полу-
ченных ранее результатов.
Следствие 5.4.
При предположениях 5.11 процесс (
q
и
)
0
≤
и
≤
T
(см.
утверждение 5.1) единственным образом определяется двумя процес-
сами (
r
и
)
0
≤
и
≤
T
и (
Р
(
и
,
Т
))
0
≤
и
≤
T
на множестве
S
с
= {(
и
,
ω
)
|
σ
и
(
ω
)
≠
0}.
Доказательство. Пункт в) в утверждении 5.2,
µ
t
−
r
t
+
σ
t
q
t
= 0,
просто доказывает следствие.
Начиная с этого места, зарезервируем символы
µ
t
и
σ
t
для эле-
ментов дифференциала
Р
, т. е.
dР
(
t
,
Т
) =
µ
t
Р
(
t
,
Т
)
dt
+
σ
t
Р
(
t
,
Т
)
dВ
t
.
Так как единственность для
q
эквивалентна единственности для
Q
, предположение
т
⊗
Р
= 0 по следствию, приведенному выше, га-
рантирует единственность
Q.
Обратное утверждение является более
формальным.
Теорема 5.4.
Для единственности нейтральной к риску вероятно-
стной меры
Q
необходимо иметь
т
⊗
Р
(
{
(
и
,
ω
)
|
σ
и
(
ω
) = 0
}
) = 0.
Доказательство этой теоремы здесь опускаем.
Теорема 5.4 обеспечивает достаточное условие для возможности
арбитражного определения цены любого актива
.
Утверждение 5.4.
При выполнении предположений 5.11, если
т
⊗
Р
(
{
(
и
,
ω
)
|
σ
и
(
ω
) = 0
}
) = 0,
тогда для всякого элемента
g
из
L
2
(
Ω
,
F
Т
,
Р
) может быть определена
цена посредством арбитража. Эта цена
π
(
g
) дается выражением
π
(
g
) =
−
−
∫∫∫
T
u
T
uu
T
u
duqdBqdurgE
0
2
00
2
1
expexp ,
где
q
и
=
−
(
µ
и
−
r
и
)/
σ
и
;
dР
и
=
µ
и
Р
и
dt
+
σ
и
Р
и
dВ
и
.
Доказательство.
Формула определения цены, установленная
выше, является эквивалентной равенству
π
(
g
) =
−
∫
T
uQ
durgE
0
exp и
единственность представляющей меры влечет, что цена каждого эле-
мента из
L
2
может быть определена арбитражным способом.

226
Единственность представляющей меры относится к плотности
«устойчивого» пространства, порождаемого
М
: из единственности
следует, что
М
является компактным в
L
2
(
Ω
,
F
Т
,
Р
).
Для
g ∈ L
2
(
Ω
,
F
Т
,
Р
) его цена в момент
и
,
и
> 0, может быть опре-
делена следующим образом. При предположении (*) и
т
⊗
Р
(
S
) = 0
цена
Y
и
элемента
g
в момент
и
должна быть такой, что система оста-
ется жизнеспособной , если добавляется стоимость
Y
и
ехр
(
)
∫
−
u
s
dsr
0
.
Отсюда она должна быть мартингалом при
Q
. Поэтому
Y
и
= ехр
∫
u
s
dsr
0
ρ
и
−
1
Е
ρ
−
∫
uT
T
s
Fdsrg
0
exp .
Если
g
ехр
(
)
∫
−
T
u
dur
0
ограничено, то
Y
и
=
Е
−
−
∫∫∫
u
T
u
s
T
u
ss
T
u
s
FdsqdBqdsrg
2
2
1
expexp .
Алгоритм определения цены, данный в утверждении 5.4, сводит-
ся к следующему: «просто интегрируйте дисконтированную стои-
мость актива в момент
Т
по отношению к мере
Q
», что объясняет тер-
мин «нейтральная к риску вероятностная мера
Q
».
Идентификация процесса мгновенной процентной
ставки с помощью процесса цены облигации
Сформулируем часто используемое утверждение о мгновенной
процентной ставке в момент
s
, являющейся «пределом при
h
→
0
внутренней нормы прибыли в момент времени
s
на облигацию с датой
погашения
s + h
» и приведем его доказательство.
Формально бескупонная облигация, по которой владельцу вы-
плачивается 1 денежная единица в момент времени
t
<
Т
, должна быть
элементом
g
ехр
(
)
∫
−
T
t
u
dur
из
L
2
(
Ω
,
F
Т
,
Р
). Согласно утверждению 5.4
(§ 2), ее цена в момент
и
,
и
<
t
, определяется выражением
Р
(
и
,
t
) =
Е
−
−
∫∫∫
u
T
u
s
T
u
ss
t
u
s
FdsqdBqdsr
2
2
1
expexp
.
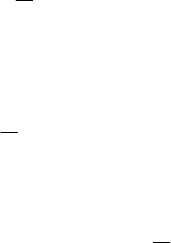
227
В момент
и
,
и
>
t
, цена задается просто в виде
−
∫
u
t
u
dur
exp .
Теорема 5.5.
При предположениях 5.11, если
т
⊗
Р
(
S
) = 0, то:
а)
()
u
h
rhuuP
h
=
+−
→
,ln
1
lim
0
по мере
т
⊗
Р
;
б) если
u
Tu
r
≤≤0
max
∈ L
1
(
Ω
,
F
Т
,
Q
), тогда для каждого
и
<
Т
мы имеем
()
u
h
rhuuP
h
=
+−
→
,ln
1
lim
0
почти всюду.
Доказательство этой теоремы опускаем из-за громоздкости.
Соотношение
()
u
h
rhuuP
h
=
+−
→
,ln
1
lim
0
допускает интерпрета-
цию
r
и
как процесса мгновенной процентной ставки. Это также пока-
зывает, что отсутствие арбитража возможно между «краткосрочны-
ми» облигациями и сберегательными счетами.
Единственность была необходима только для получения единст-
венного выражения для стоимости
Р
[
и
,
(
и + h
)
∧
Т
]. Если
Q
не един-
ственная и мы согласны вычислять цену всех этих облигаций с той же
мерой, тогда может быть доказана аналогичная теорема. К сожале-
нию, если
Q
не является единственной , то нет экономического смысла
производить вычисления с одинаковой вероятностной мерой.
§ 3. СЛУЧАЙ, КОГДА МГНОВЕННАЯ ПРОЦЕНТНАЯ
СТАВКА ЯВЛЯЕТСЯ ДИФФУЗИОННЫМ
ПРОЦЕССОМ
Предположим, что мгновенная процентная ставка следует диф-
фузионному процессу, и сопоставим получающиеся результаты с
обычным дифференциальным подходом в финансовой экономике, со-
блюдая математический уровень строгости при определениях и дока-
зательствах. Основным результатом будет получение дифференци-
ального уравнения в частных производных для цены облигаций как
функции только от мгновенной процентной ставки. Для простоты до-
казательств, мы рассмотрим только стационарный случай. Докажем,
что при условиях регулярности:
а) процесс сберегательного счета квадратично интегрируемый;
228
б) процесс цены облигации – не более чем зависящая от времени
детерминированная функция процесса мгновенной процентной став-
ки, если и только если то же верно для цены процесса риска;
в) при предположениях дифференцируемости детерминирован-
ная функция пункта б) удовлетворяет параболическому уравнению в
частных производных, а процесс цены облигации – тоже диффузион-
ный процесс.
Из предположения диффузии следует, что процесс мгновенной
процентной ставки (
r
t
)
t
является марковским. Не будем использовать
каноническое представление, которое становится неизбежным для бо-
лее строгого анализа. Марковское свойство выражается здесь в сле-
дующем виде.
Марковское свойство.
Для всякой ограниченной измеримой
функции
g
на
Ω
, зависящей от
r
и
, для
t ≤
и
≤
Т
при заданном
t
, т. е.
g
,
измеримой относительно
σ
-алгебры
σ
(
r
и
;
t ≤
и
≤
Т
), имеет место ра-
венство
Е[g|F
t
]
=
Е[g|r
t
]
.
Для простоты принимаем, что коэффициенты дрейфа и диффузии
для
dr
t
принадлежат классу
С
∞
, и, что более важно, за конечное время
процесс
r
t
никогда не достигает ни 0 ни +
∞
.
Предположение 5.12.
Процесс (
r
t
)
t
следует стационарному диф-
фузионному процессу
dr
t
=
а
(
r
t
)
dt + b
(
r
t
)
dВ
t
,
где
а
,
b
являются
С
∞
функциями на (0,
+∞
) и
b
< 0. Кроме того, для
каждой стартовой точки
r
0
=
х
Р
{
0 <
Tt
≤≤0
inf
r
t
≤
Tt
≤≤0
sup
r
t
< +
∞}
= 1.
Условия на
а
и
b
, гарантирующие отсутствие взрывного измене-
ния
r
t
, известны как условия Феллера. Известно, что для данных
а
и
b
и
х
> 0 имеется только одно строгое решение дифференциального
уравнения предположения 5.12, такое, что
r
0
=
х.
Из единственности решения следует, что предположения 5.2, 5.3
и 5.9 вытекают из предположения 5.12. Докажем это. У нас имеется
функция
g
: (0, +
∞
)
→
R из
С
∞
с
g
′
=
1/6
f
; процесс
Х
t
= g
(
r
t
) удовле-
творяет уравнению
dХ
t
=
(
g′
(
r
t
)
а
(
r
t
) +
g
″
(
r
t
)
b
2
(
r
t
)/2)
dt + g′
(
r
t
)
b
(
r
t
)
dВ
t
,
но так как
g′
≠
0, функция
g
имеет обратную
h
, т. е.
r
t
= h
(
Х
t
) и
dХ
t
= α
(
Х
t
)
dt + dВ
t
229
для некоторой функции
α
из
С
∞
. Последнее уравнение показывает, что
для 0
≤
и
≤
s
процесс (
В
и
)
0
≤
и
≤
s
может быть регенерирован из процесса
(
Х
и
)
0
≤
и
≤
s
, а значит, и из процесса (
r
и
)
0
≤
и
≤
s
. Разности (
В
и
−
В
t
)
t
≤
и
≤
s
мо-
гут быть также регенерированы из (
r
и
)
t
≤
и
≤
s
. Наконец, очень важное
замечание для последующего использования: как бы ни определялся
стохастический интеграл
()
∫
s
t
uu
dBruf
,, эти функции зависят только
от (
r
и
)
t
≤
и
≤
s
.
Тот факт, что
b
< 0, может показаться странным, поскольку
обычно
b
интерпретируется как стандартное отклонение. Однако знак
b
является неважным, потому что, если заменить
В
t
на
−
В
t
,
b
изменяет
свой знак. Для дальнейшего использования лучше, чтобы коэффици-
ент диффузии цены
Р
(
t
,
Т
) был положительным, и так как оказывает-
ся, что последний имеет знак, противоположный к знаку
b
, принимаем
b
< 0. Тот факт, что
b
не обращается в нуль, является существенным
при описании функционирования рынка.
Достаточные условия интегрируемости
сберегательного счета
Диффузионное предположение 5.12 о процессе мгновенной про-
центной ставки не обязательно влечет свойство интегрируемости
предположения 5.4 для процесса цены облигации. Приводимая ниже
теорема устанавливает достаточное условие выполнения предположе-
ния 5.4, которое имеет разумное экономическое дополнение: ограни-
ченность коэффициента дрейфа при
dr
t
должна быть следствием эко-
номических сил, возвращающих мгновенную процентную ставку об-
ратно к «нормальным» значениям, если случается, что она становится
достаточно высоко й. В конкретных моделях даже обычно предполага-
ется
а
(
х
) < 0 для достаточно больших
х.
Теорема 5.6.
Если в предположении 5.12 коэффициент диффу-
зии
b
(.) является ограниченным и коэффициент дрейфа
а
(.) ограничен
сверху на бесконечности, тогда для всякого
γ
> 0 и
х
> 0 процесс,
стартующий из
х
(т. е.
r
0
=
х
), удовлетворяет неравенству
Е
≤≤
u
Tu
r
0
maxexp
γ
<
∞
.
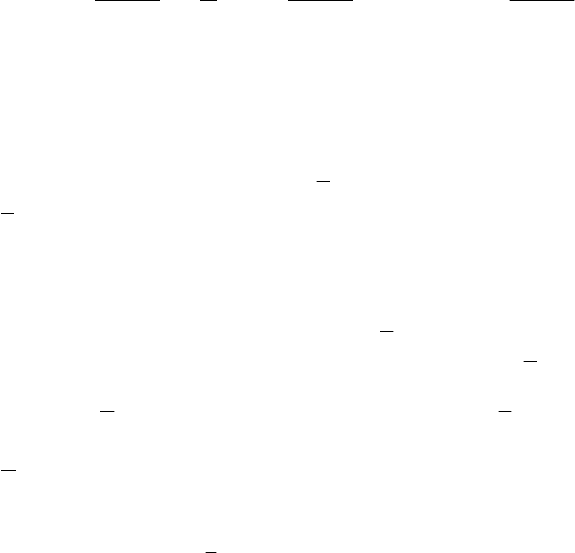
230
В частности, для каждого начального значения
r
0
мгновенной
процентной ставки финальное значение сберегательного счета
∫
T
u
dur
0
exp является элементом
L
2
(
Ω
,
F
Т
,
Р
).
Доказательство.
а) Для доказательства теоремы нам нужно по-
казать, что процесс с положительными значениями
X
u
= exp(
γr
u
) удов-
летворяет неравенству
E
(max
0
≤
u
≤
T
X
u
2
)
<
∞
.
б) Формула Ито позволяет записать уравнение
uu
u
u
uu
u
dBX
X
bduX
X
b
X
adX
γ
γ+
γ
γ+
γ
γ=
lnln
2
1
ln
22
или
uuuuuu
dBXXduXXdX
)()(
β
+α=
для некоторых функций
α
и
β
из
С
∞
на (0,
∞
), где для некоторых
K
> 0
|β
(
x
)
| <
K
, и для некоторых чисел
x
> exp(
γx
0
) функция
α
(
х
)
≤
K
для
всех
х
≥
x
. Покажем, что ограниченность
α
(
х
) на бесконечности ком-
пенсирует возможные большие значения
X
s
в
∫
α
u
s
dsX
0
)(.
в) Пусть
и
будет произвольным моментом времени между 0 и
Т
.
Тогда для
ω
∈
Ω
тако го, что
X
u
(
ω
)
>
x
, введем последний момент
времени перед
и
, когда выполнялось равенство
X
s
=
x
, соотношением
и
= e
(
u
,
ω
) = sup{
t |
t
<
u
,
X
t
(
ω
)
≤
x
}.
(Так как
и
= e
(
u
,
ω
) не является временем остановки, с ним надо об-
ращаться внимательно.) Для такого
ω
получим
X
u
(
ω
)
≤
X
0
(
ω
) +
dsXX
u
ss
)())((
0
ωωα
∫
+
dsXK
u
s
)(
0
ω
∫
+
+ )()(
0
ω
β
∫
u
sss
dBXX
.
Так как
dsXX
ue
ss
)())((
),(
0
ωωα
∫
ω
=
X
e
(
u
,
ω
)
(
ω
)
−
X
0
(
ω
)
−
)),,((
0
)(
ωω=
β
∫
uet
t
sss
dBXX
,
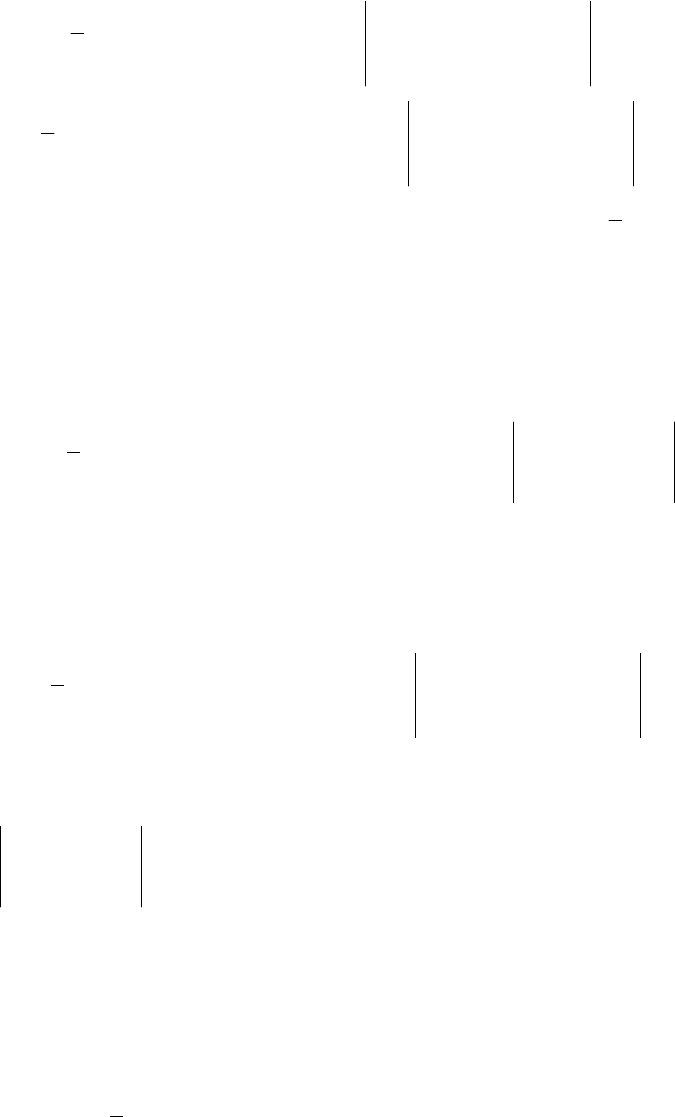
231
выполняются следующие неравенства:
X
u
(
ω
)
≤
x
+
dsXK
u
s
)(
0
ω
∫
+ 2 )()(max
0
0
ω
β
∫
≤≤
t
sss
ut
dBXX
,
X
u
2
(
ω
)
≤
3
x
2
+
dsXТK
u
s
)(3
0
22
ω
∫
+ 12
2
0
0
)()(max
ω
β
∫
≤≤
t
sss
ut
dBXX
,
последнее из которых имеет место для
ω′
таких, что
X
и
(
ω′
)
≤
.
x
г) для любых
N
введем величины
τ
N
≡
inf{
t
|
X
t
>
N
}
∧T
,
Y
u
≡
.
N
u
X
τ∧
Тогда из последнего неравенства пункта в) будем иметь, что
Y
u
2
=
2
N
u
X
τ∧
≤
3
x
2
+
dsXТK
N
u
s
)(3
0
22
ω
∫
τ∧
+ 12
2
0
0
)(max
∫
β
τ∧≤≤
t
sss
ut
dBXX
N
,
которое показывает, что упомянутое неравенство остается справедли-
вым, когда
Х
заменяется на
Y
. Кроме того, правая часть неравенства
возрастает с увеличением
и
, что дает
2
max
s
us
Y
≤
≤
3
x
2
+
dsYТK
u
s
∫
0
22
3 + 12
2
0
0
)()(max
ω
β
∫
τ∧≤≤
t
sss
ut
dBXX
N
.
д) По неравенству Дуба имеем
β
∫
≤≤
2
0
0
)(max
t
sss
ut
dBYYE
≤
4
β
∫
2
0
)(
u
sss
dBYYE
≤
4
∫
u
s
dsYEK
0
22
][.
Последнее неравенство следует из свойства изометрии и из неравен-
ства
|β
(
x
)
| ≤
K
.
е) Таким образом, для
ϕ
(
и
)
≡
Е
{
2
max
s
us
Y
≤
} получаем мажоранту
ϕ
(
и
)
≤
3
x
2
+
∫
u
s
dsYEТK
0
22
][3 + 48
∫
u
s
dsYEK
0
22
.][
