McMahon D. String Theory Demystified
Подождите немного. Документ загружается.


66
String Theory Demystifi ed
P
τ
µ
has an immediate physical interpretation. It is the momentum density of the
string. We integrate along the length of the string fi xing
τ
to get the total momentum
carried by the string, which we label
p
µ
:
pdP
µ
σ
µ
τ
σ
=
∫
0
1
(3.23)
The other conserved current associated with the global symmetries of the action
comes from invariance under Lorentz transformations. In this case
δω
µµ
ν
ν
XX=
We can show that the lagrangian in Eq. (3.19) is invariant under a Lorentz
transformation in the following way:
δηδ ηδη
α
µ
β
ν
µν α
µ
β
ν
µν α
µ
β
ν
µ
∂∂ =∂ ∂ +∂ ∂
()
()
()
XX X X X X
νν
α
µ
β
ν
µν α
µ
β
ν
µν
α
µ
ρ
ρ
δη δη
ω
=∂ ∂ +∂ ∂
=∂
() ()
(
XX X X
X
))
()
∂+∂∂
=∂∂ +
β
ν
µν α
µ
β
ν
λ
λ
µν
µ
ρα
ρ
β
ν
µν
ηωη
ωη
XXX
XX
ωωη
ωω
ν
λα
µ
β
λ
µν
νρ α
ρ
β
ν
µλ α
µ
β
λ
∂∂
=∂∂ +∂∂
XX
XX XX (lowwer indices with
η
ωω
µν
νρ α
ρ
β
ν
ρλ α
ρ
)
=∂∂ +∂XX X∂∂→
=∂∂
β
λ
νρ α
ρ
β
µρ
ω
X
X
(relabel dummy indices )
XXXX
ν
ρν α
ρ
β
ν
ωλν
+∂∂ →(relabel dummy indices )
==∂∂ +∂∂ =
ωω ω
νρ α
ρ
β
ν
νρ α
ρ
β
ν
α
XX XX0 (antisymmetry
βββα
ω
=− )
So the lagrangian is invariant under a Lorentz transformation, but what are the
currents? This is easy to fi nd, since
L
T
hh X X
L
P
P
=− − ∂ ∂
⇒
∂
∂∂
2
αβ
α
µ
β
ν
µν
α
η
XX
T
hh X
T
hh P
µ
αβ
β
ν
µν
αβ
β
µ
η
(
)
=− − ∂ =− −
22
Using
εδ
µν
µ
ν
α
α
µµ
JL XX
P
=∂ ∂∂[/( )]
where
δ
ω
µµ
ν
ν
XX=
together with the anti-
symmetry of
ω
µ
ν
, we conclude that the Lorentz current is
JTXPXP
α
µν µ
α
νν
α
µ
=−
()
(3.24)

CHAPTER 3 Symmetries and Worldsheet Currents
67
We have introduced the energy-momentum tensor and looked at some conserved
currents that arise due to symmetries of the lagrangian. The next major piece of
the dynamics puzzle is the hamiltonian which governs the time evolution of the
worldsheet. It can be written down simply using formulas from classical mechanics:
HdXPL
T
dX X
P
=−
(
)
=+
′
(
)
∫∫
σσ
µτ
µ
σσ
00
22
11
2
(3.25)
The Hamiltonian
In this chapter we have extended our classical analysis of the string. We did this by
introducing the energy-momentum tensor and by describing the symmetries of the
Polyakov action. Then we derived conserved currents of the worldsheet, and wrote
down the hamiltonian. In the next chapter, we will conclude our classical description
of the string by writing down mode expansions of the hamiltonian and energy-
momentum tensor, and describing the Virasoro algebra. After writing down a mass
formula for the string, we will proceed to quantize the theory.
Summary
1. Let
σ
σεσ
ααα
→
′
+ (
)
be an infi nitesimal reparameterization. Considering
only terms that are fi rst order in
ε
α
, fi nd the variation of the worldsheet
metric
h
αβ
.
2. Assuming that you can move the derivative
dd/
τ
inside the integral in
Eq. (3.23), explain conservation of momentum for the cases of the open
and closed string.
3. The energy-momentum tensor has zero trace. Show that this is a
consequence of Weyl invariance.
4. Consider light-cone coordinates and derive the Virasoro constraints for the
energy-momentum tensor.
5. Consider the Lorentz current
J
α
µν
in Eq. (3.24). What is the equation that
describes that the current is conserved? What are the conserved charges and
what do they describe?
Quiz
This page intentionally left blank
String Quantization
At this point we have the classical physics of the string in place. The next step
toward a quantum theory is, of course, to quantize the string. We will start off by
looking at a quantum theory of a single string. From quantum fi eld theory you recall
that this procedure is known as fi rst quantization. This is opposed to the procedure
called second quantization, which is a viewpoint of quantizing fi elds (see Quantum
Field Theory Demystifi ed for a review). The difference in the two approaches will
be on how we view the X
m
(s, t ). If we take them to be fi elds, then the quantization
procedure is second quantization. If we take them to be space-time coordinates, as
we have so far, then the process is fi rst quantization. This is the procedure we will
apply in this chapter. There are several different approaches to quantization of the
string, each with their own accompanying diffi culties and problems. The main
approaches used are called covariant quantization, light-cone quantization, and
BRST quantization. We consider the fi rst two approaches here, and will discuss
BRST quantization later.
CHAPTER 4
Copyright © 2009 by The McGraw-Hill Companies, Inc. Click here for terms of use.

70
String Theory Demystifi ed
Covariant Quantization
The procedure known as covariant quantization will be familiar to you from your
studies of ordinary quantum mechanics. In a nutshell, this is the imposition of
commutation relations on position and momentum. So, using this procedure we
continue with the notion that
X
µ
στ
(,
)
are space-time coordinates, but we need to say
what we are taking as the momentum. This can be done in the standard way using
lagrangian dynamics. Let
π
στ
µ
(, )
be the momentum carried by the string. Given a
lagrangian density L we can calculate the momentum from the
X
µ
στ
(,
)
using
πστ
µ
τ
µ
(, )=
∂
∂∂
()
L
X
This is easy to calculate using the Polyakov action as written in Eq. (2.31):
S
T
dXXXX
L
T
XX
P
=∂∂−∂∂
()
⇒= ∂ ∂ −∂
∫
2
2
2
σ
τ
µ
τµ σ
µ
σµ
τ
µ
τµ σσ
µ
σµ
XX∂
()
So we see that the conjugate momentum is
πστ
µ
τ
µ
τµ
(, )=
∂
∂∂
()
=∂
L
X
TX
With this defi nition in hand, we are in a position to quantize the theory. To do this
we take the approach used in quantum fi eld theory, namely, impose equal time
commutation relations on the position and momenta. In ordinary quantum mechanics
the position and momentum coordinates satisfy
[, ] [, ] [, ]
[, ] [, ] [,
xp yp zp i
xx yy z
xyz
===
==zzxyxzyz
pp pp
xx yy
][,][,][,]
[, ][, ]
====
=
0
======[, ][, ][, ][, ]pp pp pp pp
zz xy xz yz
0
where we have set
? =
1
. If we denote the coordinates as x
i
where i = 1, 2, 3 then
these relations can be written compactly as
[, ]
[, ][, ]
xp i
xx pp
ij ij
ij i j
=
==
δ
0

CHAPTER 4 String Quantization
71
Here, d
ij
is the Kronecker delta. Now we apply these relations to the string, with two
crucial differences. First, we have a relativistic theory and hence we let
δη
µν
ij
→
.
Moreover, we expect that position and momentum will commute when they are
taken to be at different spatial locations of the string. That is, let s and s ′ be two
different locations on the string. Since we are taking equal time commutation
relations, we let the time coordinate be τ for both position and momentum. Then
[ (,), ( ,)]X
µν
στ π σ τ σ σ
′
=≠
′
0for
Now, to ensure that the position and momentum don’t commute at the same
spatial location, we use the Dirac delta function d ( s − s ′). So the equal time
commutation relations are:
Xi
X
µν µν
µ
στ π σ τ ηδσ σ
στ
(, ), ( , ) ( )
(, )
′
⎡
⎣
⎤
⎦
=−
′
,, ( ,) (,), ( ,)X
νµν
στ πστπστ
′
⎡
⎣
⎤
⎦
=
′
⎡
⎣
⎤
⎦
= 0
(4.1)
To summarize, remember that
• t is the same for
X
µ
στ
(,
)
and
π
στ
ν
(,)
′
.
• The presence of the Dirac delta function
δ
σσ
()−
′
ensures that the
coordinates and momenta do commute at different points σ along the
string—the commutation relations are only nonzero when position and
momentum are evaluated at the same point on the string.
• The presence of
η
µν
comes from the fact we have a relativistic theory.
Ultimately, we want to write down commutation relations for the modes of the
string. This can be done most easily by transitioning to the light-cone coordinates
σ
τσσ τσ
+−
=+ =−,
. First, using
∂= ∂+∂ ∂= ∂−∂
+−
12 12/( ) /(
)
τσ τσ
and
, we
can invert to write
∂+∂=∂ ∂−∂=∂
+− +−
τσ
(4.2)
In the case of
X
νν
στ πστ
(,) (,
)
′′
and
, we will have ∂′
+
= 1/2 (∂
τ
+ ∂
σ′
) and
∂′
−
= 1/2 (∂
τ
− ∂
σ′
). Using Eq. (4.2), we can write the commutation relation
[ (,), ( ,)] ( )Xi
µν µν
στ π σ τ ηδσ σ
′
=−
′
in a new way:
iX X
ηδσ σ στ πσ τ στ
µν µ ν µ
( )[ (,), (,)][ (,)−
′
=
′
= ,, ( , ) ]
[(,),( )(
TX
TX X
∂
′
=
′
∂+
′
∂
′
+−
τ
ν
µν
στ
στ σ
,, ) ]
[ (,), ( ,)] [ (,)
τ
στ σ τ στ
µν µ
=
′
∂
′
+
+
TX X TX ,, ( , ) ]
′
∂
′
−
X
ν
στ

72
String Theory Demystifi ed
Now we compute the derivative of
[ (,), ( ,)] ( )Xi
µν µν
στ π σ τ ηδσ σ
′
=−
′
with
respect to s. Since
X
ν
στ
(,)
′
is not a function of s, only
X
µ
στ
(,
)
is affected.
Proceeding and again using Eq. (4.2) we fi nd
iTXX
η
σ
δσ σ σ τ σ τ
µν
σ
µν
∂
∂
−
′
=∂
′
∂
′
+
( ) [ (,), ( ,)]
[ (,), ( ,)]
[( ) (
+ ∂
′
∂
′
=∂−∂
−
+−
TX X
TX
σ
µν
µ
στ σ τ
σστ σ τ
στ
ν
µ
,), ( ,)]
[( ) ( , ),
′
∂
′
+∂−∂
+
+−
X
TX (,)]
[ (,), ( ,)]
′
∂
′
=∂
′
∂
′
−
++
X
TX X
ν
µν
στ
στ σ τ
−−∂
′
∂
′
+∂
−+
+
TX X
TX
[ (,), ( ,)]
[(,),
µν
µ
στ σ τ
στ
′′
∂
′
−∂
′
∂
′
−−−
XTXX
νµν
στ στ στ
(,)] [ (,), (,)]
Now we can utilize the commutation relation for the conjugate momenta in
Eq. (4.1). We have
0 =
′
=∂ ∂[ (,), ( ,)][ (,),
πστπστ στ
µν
τ
µ
τ
ν
TX TX((,)]
[ (,), ( ,)]
[
′
=∂ ∂
′
=∂
στ
στ σ τ
τ
µ
τ
ν
τ
TX X
TX
2
µµ
τ
ν
στ σ τ
( , ), ( , )]∂
′
X
(Since it equals zero,, we divide
by for later convenience)T
T= [(∂∂+∂
′
∂+
′
∂
′
=∂
+− +−
+
) (,),( ) ( ,)]
[
XX
TX
µν
µ
στ σ τ
(( , ), ( , )] [ ( , ), (
στ σ τ στ
νµν
′
∂
′
+∂
′
∂
++−
XTXX
′′
+∂
′
∂
′
+∂
−+
στ
στ σ τ
µν
,)]
[ (,), ( ,)] [TX X T
−−−
′
∂
′
XX
µν
στ σ τ
( , ), ( , )]
Now since
[ (,), ( ,)]
πστπστ
µν
′
= 0
, let’s form the sum [p
m
(s, t), p
n
(s ′, t)] +
ih
mn
(/ s ) d ( s - s′). We obtain
[ (,), ( ,)] ( )
[
πστπστ η
σ
δσ σ
µν µν
µ
′
+
∂
∂
−
′
=∂
+
i
TX(( , ), ( , )] [ ( , ), (
στ σ τ στ
νµν
′
∂
′
+∂
′
∂
++−
XTXX
′′
+∂
′
∂
′
+∂
−+
στ
στ σ τ
µν
,)]
[ (,), ( ,)] [TX X T
−−−
+
′
∂
′
+∂
XX
TX
µν
µ
στ σ τ
στ
( , ), ( , )]
[(,),
′′
∂
′
−∂
′
∂
′
+−+
XTXX
νµν
στ στ στ
( ,)] [ (,), ( ,)]
[
(
,
)
,
(
,
)
][
(
,+∂
′
∂
′
−∂
+
−−
TX X TX
µν µ
στ σ τ στ
))
,
(
,
)
]
′
∂
′
−
X
ν
στ

CHAPTER 4 String Quantization
73
That is,
iTXX
η
σ
δσ σ σ τ σ τ
µν µ ν
∂
∂
−
′
=∂
′
∂
′
++
( ) [ (,), (,)]2 ++∂
′
∂
′
+−
2TX X[ (,), ( ,)]
µν
στ σ τ
It is also straightforward to show that
[ (,), ( ,)] ( )
[
πστπστ η
σ
δσ σ
µν µν
′
−
∂
∂
−
′
=∂
−
i
TX2
µµν µ
στ σ τ στ
( , ), ( , )] [ ( , ),
′
∂
′
+∂
′
∂
−−+
XTXX2
νν
στ
(,)]
′
In the chapter quiz, you will have the opportunity to show that [
+
X
m
(s, t ),
−
X
n
(s, t )] = [
−
X
m
(s, t ),
+
X
n
(s′, t )] = 0. Therefore the commutation relations are
[ (,), ( ,)] ( )∂
′
∂
′
=
∂
∂
−
′
++
XX
i
T
µν
µν
στ σ τ
η
σ
δσ σ
2
(4.3)
[ (,), (,)] (∂
′
∂
′
=−
∂
∂
−
′
−−
XX
i
T
µν
µν
στ σ τ
η
σ
δσ σ
2
))
(4.4)
[ (,), ( ,)][ (,),∂
′
∂
′
=∂
′
∂
+− −+
XX X
µν µ
στ σ τ στ
XX
ν
στ
(,)]
′
= 0
(4.5)
Using Eqs. (4.3) to (4.5), deriving commutation relations for the modes, which will
help us get to the quantum physics, will be a much simpler matter. In order to derive
the commutation relations, we will need the following expression for the Dirac
delta function:
δ
κ
()=
=−∞
∞
∑
x
z
e
ikx
1
2
Recalling Eq. (2.47), which told us that we can write the equations for the string
in terms of left-moving and right-moving modes:
XXX
LR
µµµ
στ στ στ
(, ) (, ) (, )=+
Notice the left-moving modes are functions of
σ
+
only, while the right-moving
modes are functions of
σ
−
only, so that
∂=∂ ∂=∂
++ −−
XX XX
LR
µµ µµ
στ στ στ στ
(, ) (, ) (, ) (, ))
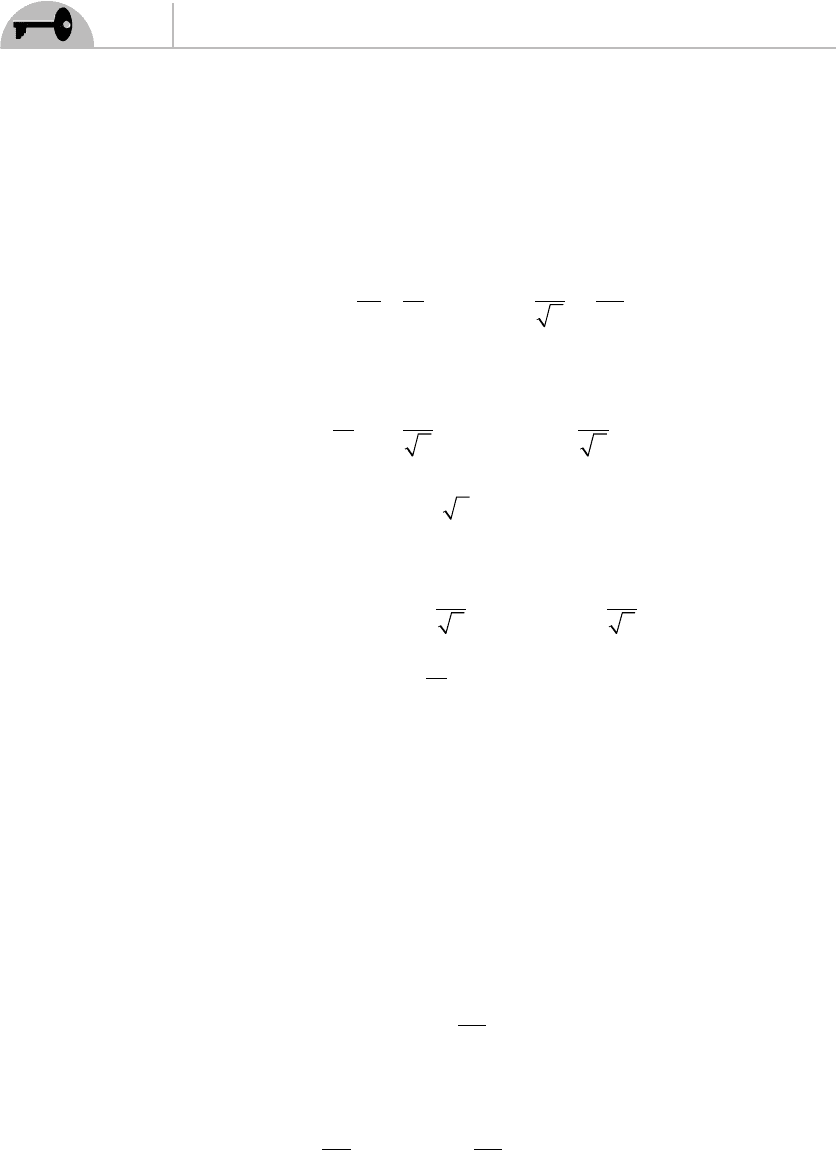
74
String Theory Demystifi ed
COMMUTATION RELATIONS FOR THE CLOSED STRING
We will derive the commutation relation [Eq. (4.3)] for the modes explicitly, and
simply state the results in the other cases. Hence we write down the left-moving
modes [Eq. (2.55)] which are functions of
σ
+
. The left-moving modes are restated
here in the case of the closed string
X
x
p
i
m
e
L
ssm
im
µ
µ
µ
µ
τσ
στ τ σ
α
(, ) ( )
()
=+ ++
−+
22
2
2
CC
mm≠
∑
0
(4.6)
Now since
σ
τσ
+
=+
, the derivative is
∂=+ =
+
−+
≠
∑
Xp e
L
ss
m
im
m
s
µµµτσ
στ α α
(, )
()
CC C
2
0
2
22
mm
im
m
e
µτσ
−+
=−∞
∞
∑
()
(4.7)
To get the last step, we used
α
µ
µ
0
2= (/ )C
s
p
. Now let’s calculate the left-hand side
of Eq. (4.3). We have
[ (,), ( ,)]
()
∂
′
∂
′
=
++
−+
XX e
s
m
im
m
µν µτσ
στ σ τ α
C
2
==−∞
∞
−+
′
=−∞
∞
−
∑∑
⎡
⎣
⎢
⎤
⎦
⎥
=
,
()
C
C
s
m
im
m
s
e
e
2
2
2
α
ντσ
iim n
mn
im n
mm
e
()
,
()
,
+
=−∞
∞
−+
′
∑
⎡
⎣
⎤
⎦
τσσµν
αα
But, this must be proportional to
(/ ) ( )∂∂ −
′
σδσ σ
, and furthermore, the term on the
right-hand side of Eq. (4.3) does not depend on
τ
. So, we have to remove the
τ
dependence. We can do so by noting that
emn
im n−+
→=−
()
τ
1 when
We will be able to enforce this condition by introducing the Kronecker delta
term
δ
mn+ ,
0
, which is 1 when
mn=−
and 0 otherwise. Furthermore, we take note of
the following expression for the Dirac delta function:
δσ σ
π
σσ
()
()
−
′
=
−−
′
=−∞
∞
∑
1
2
e
im
m
(4.8)
Notice that
∂
∂
−
′
=−
−−
′
=−∞
∞
∑
σ
δσ σ
π
σσ
()
()
i
me
im
m
2
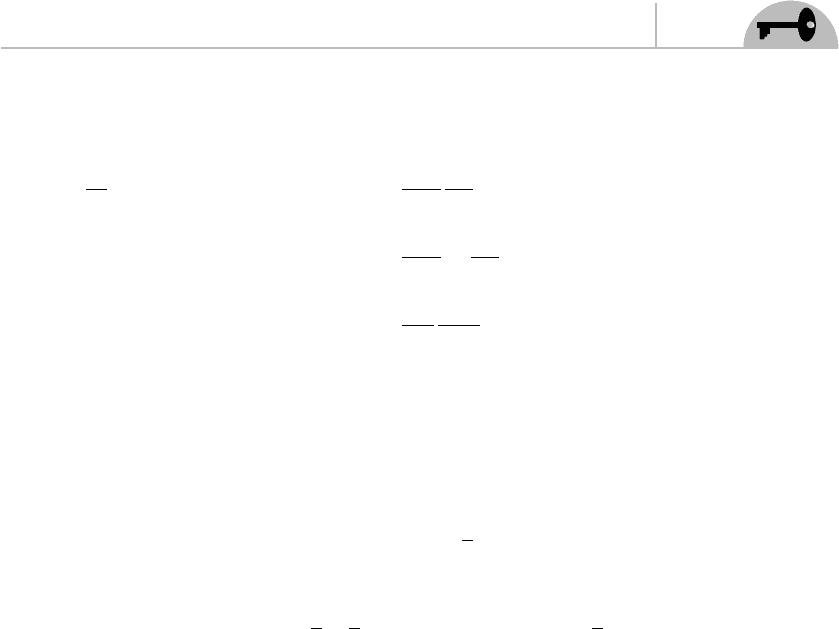
CHAPTER 4 String Quantization
75
Using Eqs. (4.3) and (4.8) together with our previous result, we have
C
s
im n
mn
im n
mm
ee
2
2
−+
=−∞
∞
−+
′
∑
=
()
,
()
[, ]
τσσµν
αα
ii
T
i
T
i
me
im
m
η
σ
δσ σ
η
π
µν
µν
σσ
2
22
∂
∂
−
′
=−
−−
′
=−∞
()
()
∞∞
−−
′
=−∞
∞
∑
∑
⎛
⎝
⎜
⎞
⎠
⎟
=
η
π
µν
σσ
2
1
2 T
me
im
m
()
We have also used Eq. (2.50) to relate
C
s
and the string tension T. This gives us
the commutation relation for the modes
αα η δ
µν µν
mn mn
m,
,
⎡
⎣
⎤
⎦
=
+ 0
Equation (4.5) can be used to show that the
αα
µν
mn
and
commute. We can write all
of the commutation relations for the modes of the closed string as
αα ηδ αα ηδ
µν µν µν µν
mn mn mn m
mm,,
,
⎡
⎣
⎤
⎦
=
⎡
⎣
⎤
⎦
=
++0 nnmn,
,
0
0
αα
µν
⎡
⎣
⎤
⎦
=
(4.9)
In the chapter quiz you will also derive a commutation relation for the center-of-
mass position and momentum of the string
[, ]xp i
µν µν
η
=
COMMUTATION RELATIONS FOR THE OPEN STRING
In the case of the open string, it can be shown that together with
[, ]xp i
µν µ
ν
η
=
, the
commutation relations are
αα ηδ
µν µν
mn mn
m,
,
⎡
⎣
⎤
⎦
=
+ 0
(4.10)
THE OPEN STRING SPECTRUM
With the commutation relations in hand, we can proceed to fi nd the states of the
string. Because the open string case is simpler, we consider this fi rst. Notice that in
our quantization procedure where we have imposed commutation relations on the
