McMahon D. String Theory Demystified
Подождите немного. Документ загружается.


76
String Theory Demystifi ed
modes
α
α
µν
mn
(and for the closed string)
, what we have done is promote them to
operators. By extension, since the
X
µ
στ
(, )
are defi ned in terms of
α
µ
m
, the
X
µ
στ
(,
)
are now to be thought of as operators as well. Therefore the next task in our program
is to determine the state space of the system, that is the states upon which the
α
µ
m
and
by extension the
X
µ
στ
(,
)
act. This procedure is really pretty similar to what you’re
used to from your previous studies of quantum theory.
The fi rst item to notice is that the commutation relations have some similarity to
the harmonic oscillator you learned about in fi rst semester quantum mechanics.
Temporarily dispensing with our convention of setting
? =
1
, recall that we can
defi ne the creation and annihilation operators for the harmonic oscillator as
ˆˆˆˆˆˆ
†
a
m
x
i
m
pa
m
x
i
m
p=−
⎛
⎝
⎜
⎞
⎠
⎟
=+
⎛
⎝
⎜
⎞
⎠
⎟
ω
ω
ω
ω
22??
These operators satisfy the commutation relation:
[
ˆ
,
ˆ
]
†
aa =1
(4.11)
The hamiltonian of the system is given by
ˆ
ˆˆ
†
Haa=+
⎛
⎝
⎞
⎠
?
ω
1
2
We introduce the number operator
ˆ
ˆˆ
†
Naa=
which has eigenstates
n
:
ˆ
Nn nn=
(4.12)
where
n = 012, , ,...
. A system consisting of an infi nite collection of harmonic
oscillators is called a fock space.
Continuing, the number operator and its eigenstates allow us to write down the
quantized energy levels of the harmonic oscillator, which are given by
ˆˆ
Hn N n n n E n
n
=+
⎛
⎝
⎜
⎞
⎠
⎟
=+
⎛
⎝
⎜
⎞
⎠
⎟
=??
ωω
1
2
1
2
You should also recall that the system has a ground state, which is the lowest
possible energy state. This is denoted by
0
.
A comparison of Eqs. (4.9) and (4.11) indicates that we have a similar system in
the case of the string. This should not be surprising, since what else would you

CHAPTER 4 String Quantization
77
expect for a vibrating string, except a system that resembles a harmonic oscillator.
Let’s continue forward. Since
[, ]
,
αα η δ
µν µν
mn mn
m=
+ 0
, we can write
αα αα η
µν µν µν
mn m m
m,,
⎡
⎣
⎤
⎦
=
⎡
⎣
⎤
⎦
=
−
(4.13)
At this point, it is important to take a step back and recognize a key fact. The
commutation relation not only bears some resemblance to the harmonic oscillator
of quantum mechanics, but there is a very important difference. Notice that the
presence of the metric
η
µν
means that we can have negative commutators. This is
the case for the time components. That is, since
η
00
1
=−
, it follows that
αα
mm
m
00
,
−
⎡
⎣
⎤
⎦
=−
This is going to turn out to be important because it can lead to negative norm
states.
Now, in analogy with the harmonic oscillator from ordinary quantum mechanics,
we defi ne a number operator. These are given in terms of the modes as
N
mmm
=⋅
−
αα
where we take
m ≥
1
. The eigenstates of the number operator satisfy
Ni ii
mm mm
=
The total number operator is defi ned by summing over all possible
N
mm
m
=⋅
−
αα
:
NN
m
m
mm
m
==⋅
=
∞
−
=
∞
∑∑
11
αα
(4.14)
Following a procedure used in elementary quantum mechanics, we can use
N
mmm
=⋅
−
αα
together with
[, ][, ]
αα αα η
µν µν
µν
mn m m
m==
−
to show that the
α
α
µµ
−mm
and
are raising and lowering operators, respectively. This follows from
Ni i
mi
mmm mmmm
mm mm
m
αααα
αα α
αα
()
=⋅
()
=⋅ −
()
=
−
−
()
(
−−
−
=−=−
()
mm m mm
mm m m m m m m
imi
ii m i i m i
αα
αα α
)
()

78
String Theory Demystifi ed
Hence,
α
µ
m
acts like a lowering operator. A similar exercise shows that the
negative frequency mode
α
µ
−
≥
m
m,1
acts like a raising operator:
Niimi
mmm m mm
αα
−−
()
=+
()
()
The lowering operator
α
µ
m
destroys the vacuum or ground state, which is the state
with
i
m
= 0
:
α
µ
m
00=
(4.15)
We can construct higher-energy states using the raising operators which are the
negative modes,
α
µ
−
≥
m
m,
1
, that is,
ααααα
µµµµµ
−−−−−11112
000,,,
and so on. A
string state also carries momentum, so we can label a state by
ik
m
,
. Considering
the ground state, supposing that the string carries momentum
k
µ
, the momentum
operator acts as
pkkk
µµ
00,,=
(4.16)
Earlier we remarked that since the Minkowski metric
η
µν
appears in the
commutation relations, negative norm states can exist. We can demonstrate this
explicitly as follows. Consider the fi rst excited state with momentum
k
µ
, that is,
α
−1
0
0, k
. Using
()
†
αα
−
=
1
0
1
0
we fi nd the norm of this state to be
ααα
−−
==−
1
0
1
0
1
0
00 01,, ,kk k
(4.17)
We can rid the theory of the negative norm states by applying the Virasoro
constraints. The classical expressions for the Virasoro constraints are
LL
mmnn
n
mmnn
n
=⋅ =⋅
−−
∑∑
1
2
1
2
αα αα
(4.18)
In the quantum theory, the Virasoro constraints are promoted to Virasoro
operators. However, since the modes must satisfy the given commutation relations,
some care must be applied when writing the Virasoro operators as derived from the
classical expressions. The technique of normal ordering is used. This will ensure
that the eigenvalues of the Virasoro operators will be fi nite. The prescription of
normal ordering is simple:
• Move all lowering operators (positive frequency modes) to the right.
• Move all raising operators (negative frequency modes) to the left.

CHAPTER 4 String Quantization
79
A normal ordered product is denoted using two colons, that is
::
†
aa
. In the case
of the Virasoro operator, we write
L
mmnn
n
=⋅
−
∑
1
2
::
αα
L
m
will lower the eigenvalue of the number operator by m. Looking at the
commutation relation Eq. (4.10), you can see that
αα
µµ
mn n−
and
commute when
m ≠
0
. This means that when
m ≠ 0
we can simply move raising and lowering
operators where we want in the expression for the Virasoro operator because no
extra terms will be added from the commutator. Normal ordering
L
0
gives
L
nn
n
00
2
1
1
2
=+ ⋅
−
=
∞
∑
ααα
(4.19)
Now, to get this result, note that
1
2
1
2
1
2
1
2
00
1
αα αα αα αα
−
=−∞
∞
−
=
∞
⋅= ⋅+ ⋅+ ⋅
∑∑
nn
n
nn
n
n −−
=
∞
−
=
∞
=
−
∑
∑∑
=⋅+ ⋅+
n
n
nn
n
D
n
n
1
00
10
1
1
2
1
2
αα α α η
µ
µ
µ
==
∞
−
=
∞
=
∞
∑∑∑
=⋅+ ⋅+
1
00
11
1
22
αα α α
nn
nn
D
n
To get from the fi rst to the second line, the commutator for the modes was used
together with the fact that
α
α
−
⋅
n
n
represents the dot product in D space-time
dimensions. To get the normally ordered result we have thrown out the sum
Dn
n
/2
1
Σ
=
∞
.
At fi rst glance, you might think that this sum is infi nite, but regularization can be
used to compute its fi nite value. To see how this works, recall the geometric series:
ar
a
r
n
n
∑
=
−1
Taking the derivative, we have
d
dr
ar anr
d
dr
a
r
a
r
n
n
n
n
∑∑
==
−
=−
−11
2
()
Now let
a = 2
πε
/C
and multiply
Σ
n
n
=
∞
1
by
e
a−
, then
d
da
ene
d
da e
e
e
an
n
an
n
a
a
a
() ()
()
−−
−
−
−
∑∑
==
−
=
−
1
11
2
==−
11
12
2
a

80
String Theory Demystifi ed
It follows that
DnD D
n
//()/221122
4
1
Σ
=
∞
=−=−/
. Another undetermined constant
piece is missing from the difference between the general expression of
L
0
and the
normal ordered expression of
L
0
. This is a normal ordering constant which is
denoted by a. Therefore in any calculation
L
0
is replaced by
La
0
−
,
where
a
is a
constant.
The point of all this is to write down the commutation relations for the Virasoro
operators. Using Eq. (4.10), one fi nds that
[, ]( ) ( )
,
LL mnL
D
mm
m n mn mn
=− + −
++
12
3
0
δ
(4.20)
We call this commutation relation the Virasoro algebra with central extension.
The central charge is the space-time dimension D which has shown up in the second
term on the right-hand side. This is also the number of free scalar fi elds on the
worldsheet. It is clear that if
m =±0
1
,
the central extension term will vanish. This
singles out
LL L
10 1
, , and
−
which form a closed subalgebra. We call this the SL
(2, R) algebra.
The Virasoro operators can be used to eliminate unphysical states (i.e., negative
norm states) from the theory by requiring that the expectation value of
La
0
−
vanishes for a physical state
ψ
. That is, we impose the constraint
ψδψ
La
mm
−=
,0
0
for
m ≥
0
. The term
a
m
δ
,0
takes care of the fact that we only need the normal
ordering constant a in the case of
L
0
. To eliminate negative norm states, specifi c
conditions must be put on a and D, which is the origin of the “extra dimensions”
in string theory. In particular, it can be shown that negative norm states can be
eliminated if
aD==126
(4.21)
The reason that
a =1
is chosen is a bit beyond the scope we want to cover in this
book, see the references if interested in the proof.
We can proceed further to obtain a mass operator. First recall that Einstein’s
equation tells us
pp m m pp
µ
µ
µ
µ
+= ⇒=−
22
0
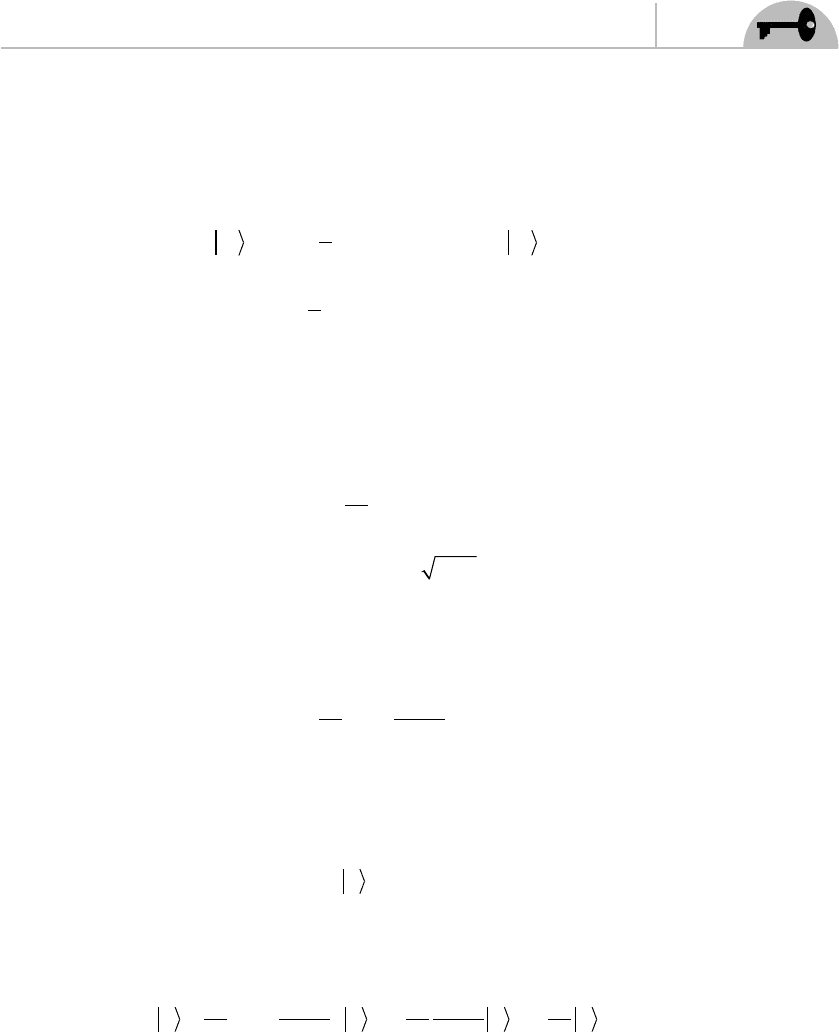
CHAPTER 4 String Quantization
81
To obtain a formula for the mass operator in string theory, which is denoted by
M
2
, we use the condition on physical states. Taking
L
n
nn00
2
1
12=+⋅
=
∞
−
/
ααα
Σ
, using
La
0
−
with
a =1
, we arrive at the condition
()La
nn
n
00
2
1
0
0
1
2
10
1
2
−=⇒+⋅−
⎛
⎝
⎜
⎞
⎠
⎟
=
⇒
−
=
∞
∑
ψαααψ
α
22
1
10+⋅−=
−
=
∞
∑
αα
nn
n
The fi rst term in this expression is nothing other than the mass squared:
(/ )12
0
22
αα
=−
′
M
where
′
=
α
π
12/( )T
. So, in bosonic string theory the “mass
shell” condition becomes
MN
2
1
1=
′
−
α
()
(4.22)
where N is the total number operator. The term
2
π
T
sets the energy scale of the
theory, it is taken to be on the order of the Planck mass. This is the origin of the high
energy scale of string theory.
It can be shown that
MN
D
2
12
24
=
′
−
−
⎛
⎝
⎜
⎞
⎠
⎟
α
Notice that setting
a =1
forces us to take
D = 26
. The number operator acts on
the ground state as
N 00=
Hence the mass of the ground state is
MN
DD
2
0
12
24
0
12
24
0
1
0=
′
−
−
⎛
⎝
⎜
⎞
⎠
⎟
=−
′
−
=−
′
ααα
So the ground state of bosonic string theory in the open string case has negative
mass. This means that the ground state is a Tachyon. This is an unphysical state
which travels faster than the speed of light. Consistency of bosonic string theory
requires that we choose
a =
1
, so the Tachyon cannot be removed from the theory.

82
String Theory Demystifi ed
It will turn out that the introduction of supersymmetry (that is the introduction of
fermionic states) into the theory will get rid of the Tachyon, giving us a realistic
string theory. We will see that this also changes the number of space-time
dimensions.
Now let’s consider the mass of the fi rst excited state. The fi rst excited state is
i
i
=
−
α
1
0
where i is a spatial index. Here,
iD=−1
2
, ...,
, and the state transforms
as a vector in space-time. You will recall from your studies of quantum fi eld theory
that a vector is a spin-1 particle that in general has
D −
1
components, the fact that this
state has
D − 2
components implies that it is a massless state. An example of a massless
vector is the photon, it only has transverse components of spin. This explains why
there are
D − 2
components rather than
D −
1
. The mass of the state is
M
DD
ii2
11
0
1
1
2
24
0
126
24
α
α
α
α
−−
=
′
−
−
⎛
⎝
⎜
⎞
⎠
⎟
=
′
−
⎛
⎝
⎜
⎞
⎠⎠
⎟
−
α
1
0
i
In order for the state to be massless,
26 24− D /
must vanish, once again setting
the number of space-time dimensions D to 26. Physicists refer to the bosonic string
theory with
aD==126,
as critical and call
D = 26
the critical dimension.
CLOSED STRING SPECTRUM
In the case of the closed string, things are a little more complicated than what
you’re used to from the harmonic oscillator in ordinary quantum theory due to the
fact that we have a second commutation relation in addition to
αα ηδ
µν
µν
mn mn
m,
,
⎡
⎣
⎤
⎦
=
+ 0
that must be satisfi ed, namely,
αα ηδ
µν
µν
mn mn
m,
,
⎡
⎣
⎤
⎦
=
+ 0
. What this is going to mean
is that we need to defi ne two number operators. These are defi ned by infi nite sums
over the modes:
NN
Rmm
m
Lmm
m
==
−
=
∞
−
=
∞
∑∑
αα αα
11
(4.23)
Together with the momentum operator
p
µ
, the number operators
NN
R
L
and
serve to characterize the state of a closed string. Let us denote a state by
nk,
. As
in the open string case, the momentum operator will act according to
pkkk
µµ
00,,=
(4.24)
Therefore, the state
0, k
of the string carries momentum
k
µ
. Turning our
attention to the number operators, fi rst let’s specify the action of the raising and
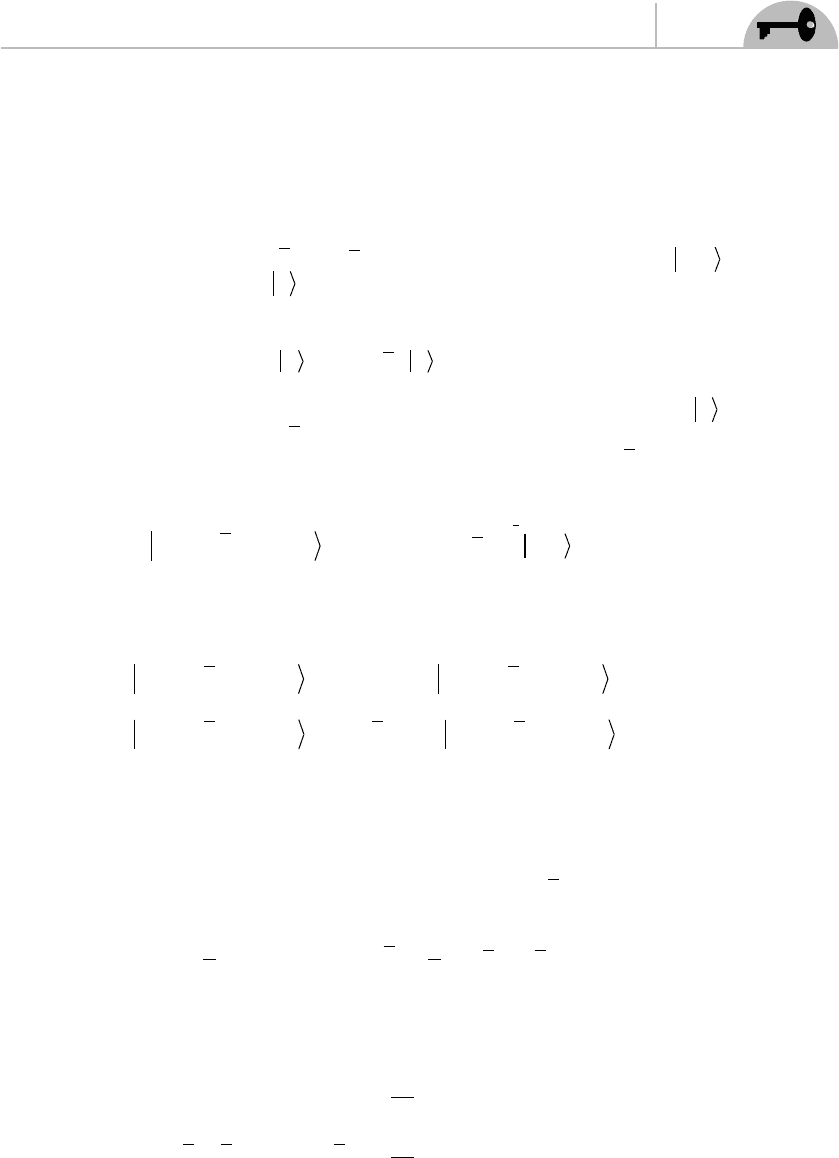
CHAPTER 4 String Quantization
83
lowering (creation and annihilation) operators. This follows what we did in the
open string case as well. Keeping
m ≥
1
, we defi ne these as follows:
•
α
µ
m
is a lowering operator.
•
α
µ
−
m
is a raising operator.
Similar roles are played by
α
µ
m
and
α
µ
−
m
. We defi ne the ground state by
00,
which is often abbreviated by
0
. Then, the lowering operators satisfy a relation
familiar from ordinary quantum mechanics:
αα
µµ
mm
00 00==
(4.25)
Note also that we can defi ne the ground state with momentum
k
µ
by writing
k
.
The raising operators
α
µ
−m
and
α
µ
−n
act to raise the eigenvalues of the number
operators
N
L
and
N
R
by m and n, respectively. So if
im(,
)
µ
and
im(, )
µ
are
integers:
imi mk
m
D
m
m
i
(, )(, ),
µµ αα
µ
µ
µ
=
()()
−
=
−
≥
∞
−
∏∏
0
1
1
ii
k0,
The number operators
N
L
and
N
R
act on this state as follows:
N i mi m k mi m i mi m
L
(,)(,), (,)(,)(,),
µµ µµµ
=
(,)(,), (,)(,)
,
k
N i mi m k mi m i mi
m
R
µ
µµ µµ
∑
= ((, ),
,
µ
µ
mk
m
∑
Once again, we will have negative norm states due to the presence of the metric
in the commutation relations. This situation can be dealt with in the same manner
used in the open string case. So we won’t go into great detail and simply state the
results, noting that in the following we take
m ≥
0
. We proceed by introducing
normal ordered Virasoro operators, but this time must include
L
m
as well:
LL
mmnn
n
mmnn
n
=⋅ =⋅
−−
∑∑
1
2
1
2
:: ::
αα αα
(4.26)
These operators satisfy commutation relations called the Virasoro algebra:
[, ]( ) ( )
[, ]
,
LL mnL
D
mm
LL
m n mn mn
mn
=− + −
=
++
12
3
0
δ
(() ( )
,
mnL
D
mm
mn mn
−+−
++
12
3
0
δ
(4.27)
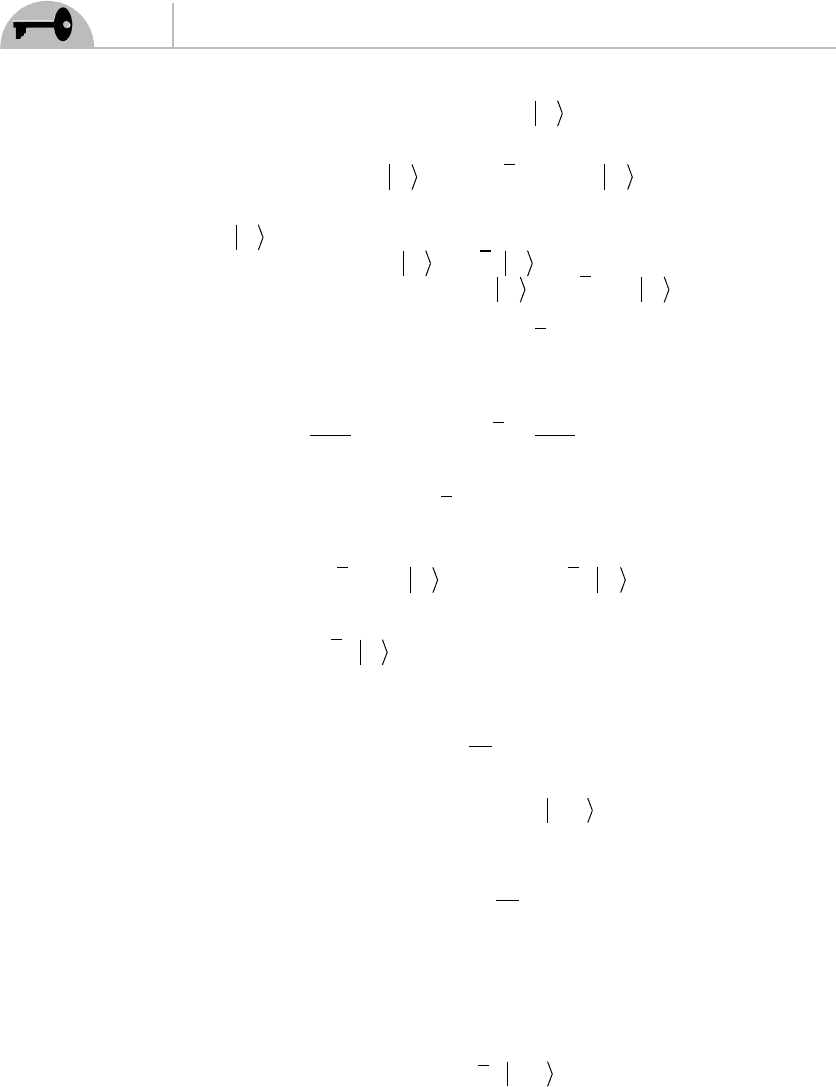
84
String Theory Demystifi ed
If the following relations are satisfi ed by a state
ψ
:
() ()
,,
La La
mm mm
−=−=
δψ δψ
00
00
(4.28)
then the state
ψ
is a physical state. That is, if
m > 0
, then the Virasoro operator
annihilates the physical state
LL
mm
ψψ
==00,
. The condition satisfi ed when
m = 0
is the “mass shell” condition,
() ,()La La
00
00−=−=
ψψ
. Once again, it
can be shown that negative norm states can be avoided in the theory provided that
aD==12
6
,
. The Virasoro operators
LL
00
and
can be written in terms of the
number operators as follows:
L
T
pp N L
T
pp N
LR00
1
8
1
8
=+=+
ππ
µ
µ
µ
µ
The sum and difference of
LL
00
and
annihilate the physical states:
()()LL a LL
00 00
20 0+− = − =
ψψ
The constraint
()LL
00
0−=
ψ
is called level matching. Using the Einstein
relations, we can arrive at an expression for a mass operator:
Mpp NN
LR
2
2
2=− =
′
+−
µ
µ
α
()
(4.29)
The ground state of the closed bosonic string is
0, k
, found when
NN
LR
==
0
.
This is a tachyon that satisfi es
M
2
4
=−
′
α
The next case to consider is
NN
LR
==1
, which is the fi rst excited state. Here
we get hints that string theory is a unifi ed theory. The fi rst excited states are massless,
so
M
2
0=
. They are derived from the ground state in the following way:
εαα
µν
µν
() ,kk
−−11
0
The object
ε
µν
()k
is a tensor which can be decomposed into symmetric
ε
µν
()
(
)
k
and antisymmetric
ε
µν
()
(
)
k
parts (see Relativity Demystifi ed if you aren’t sure about

CHAPTER 4 String Quantization
85
this). The symmetric part corresponds to a massless spin-2 particle which is the
graviton. The linearized metric
gx
ρσ ρσ ρσ
ηε
=+()
satisfi es the linearized Einstein
equations
∂∂ = ∂ =
µ
µ
ρσ
µ
µν
εε
() , ()xx00 and
. By taking the Fourier transform of
ε
µν
()
(
)
k
, it can be shown that these equations are satisfi ed.
The trace
ε
µ
µ
(
)
k
, which defi nes a scalar, is also important. This corresponds to a
massless scalar particle called the dilaton.
We now turn our attention to a different method of quantization. We began the
chapter with a discussion of covariant quantization. This method is a straightforward
application of the imposition of commutation relations. We took this approach fi rst
because it may seem familiar from your studies of ordinary quantum mechanics. In
addition, it preserves the Lorentz invariance of the theory. Physicists say that this
approach is “manifestly” Lorentz invariant, colloquially meaning that the Lorentz
invariance is obvious. The technique has the disadvantage in that negative norm
states appear. Although this is a problem, it is instructive to go through the process
of eliminating the negative norm states.
Another approach is possible which avoids the negative norm states at the cost
of losing manifest Lorentz invariance. This is called light-cone quantization. We
briefl y discuss it here, considering the open string case.
We begin by using light-cone coordinates, which were introduced in Chap. 2 in
Eq. (2.34):
X
XX
D
±
−
=
±
01
2
(4.30)
The remaining coordinates
X
i
are transverse coordinates. The center of mass
coordinate
x
µ
and momentum
p
µ
are also written as light-cone coordinates. In the
light-cone gauge, we choose
Xx p
s
++ +
=+C
2
τ
(4.31)
which leads to
α
n
n
+
=≠0 for 0
, that is, the modes are zero for
X
+
. The Virasoro
constraints will lead us to a description based on transverse oscillators. We have the
freedom to set
C
s
p
2
1
+
=
, giving the center of mass position as
Xx
p
p
µµ
µ
τ
=+
+
Light-Cone Quantization
