McMahon D. String Theory Demystified

Подождите немного. Документ загружается.

106

String Theory Demystiﬁ ed

The energy-momentum tensor of the worldsheet is a conserved quantity, meaning

that

∂=

µν

T 0

(5.31)

The energy-momentum tensor is also traceless. This means that in the coordinates

(, )zz

, the components

= 0

. The conservation condition [Eq. (5.31)] implies that

∂=∂=

zzz zzz

TT0

(5.32)

That is, the energy-momentum tensor is composed of a holomorphic and

antiholomorphic functions given by

zz zz

and

, respectively. A holomorphic

function has a Laurent series expansion, which we write as

()=

=−∞

∞

∑

(5.33)

We have written this expression in a way anticipating that the Laurent coefﬁ cients

are the Viarasoro generators. The antiholomorphic component also has a Laurent

expansion:

()=

=−∞

∞

∑

(5.34)

Worldsheet of

closed string

z plane

z=e

t+is

Figure 5.1. The worldsheet of a closed string is mapped to the z plane. A slice

through the cylinder, at a constant time, is mapped to a circle of a

ﬁ xed radius in the z plane. The radius of the circle in the z plane

corresponds to (Euclidean) time on the worldsheet.

CHAPTER 5 Conformal Field Theory Part I

107

Using standard complex analysis, this tells us that we can invert these formulas

in the following way:

zTz L

zTz

zz m

∫∫

ππ

() ())

(5.35)

The deformation of path theorem (see Complex Variables Demystiﬁ ed ) tells us

that we can shrink or expand the contour used for the integration in Eq. (5.35) and

leave the integral invariant. Since movement along the radial distance in the complex

plane corresponds to time translation, this tells us that the Virasoro operators are

invariant under a time translation, in other words the integrals [Eq. (5.35)] are

related to conserved charges.

To gain insight into the physics of the problem, we will begin by calculating

propagators for the theory. In the text we will derive the closed string propagator,

you can try the open string case in the chapter quiz.

We begin by considering the propagator or Wick expansion for

στ

)

for the

closed string. This is done by calculating

XX TXX

µν µν

στ σ τ στ σ τ

(, ), ( , ) ( (, ), ( , )

′′

)): (,) ( , ):−

′′

µν

στ σ τ

This is also called the two-point function. There are two notations you should be

aware of in this expression. The T indicates that the expression is time ordered. It is

shorthand for

TXXXX((,),(,)) (, ) ( , )(

µν

στ σ τ

µν

στ σ τθ

′′

τττ στ στθτ τ

νµ

−

′

′′ ′

−)(,)(,)( )XX

To understand what we have here, note that the Heaviside function

θθ

() , ()ttt t=> = <10 00 if if

. This expression ensures that the term which

occurs earlier in time is to the right. So if

ττ

′

, which means that

is later than

′

, then

TX X X X( (,), ( , )) (,) ( , )

µν µν

στ σ τ στ σ τ

′′

Wick Expansion

108

String Theory Demystiﬁ ed

and vice versa for the other possibility. The colons indicate normal ordering which

puts all creating operators to the left of all annihilation operators. Now consider

the fact that we can write the ﬁ elds in terms of left movers and right movers.

Then

000 0

XX XXXX

LRLR

µν µµνν

στ σ τ

(, ) ( , ) ( )( )

′′

=+ +

XXX XX XX XX

LL LR RL RR

µν µν µν µν

+++ 0

Now let’s move to the complex plane where

XXzXXz

RR LL

µµ µµ

==(), ( )

so that

0000XX XzzXzz

µν µν

στ σ τ

(,)(,) (,)(,)

′′

→

′′

. Let’s consider one term,

00XX

µν

using the expansion given in Eq. (5.30). Noting that

00=

and

[, ]xp i

µν µ

µµ

mn00 0 0 0

=> = < if and for

, we have

XX xx i z px

µ ν µν µν

=− −

µµν

µν

≠

−−

∑

′

=−+

CCln

αα

µν

≠

−

−−

∑

′

Moving from the ﬁ rst to the second line, we used

000 000 00px xp i xp i i

µ ν ν µ µν ν µ µν µν

ηηη

=−= − =−

Now the commutator of the creation and annihilation operators satisﬁ es

αα ηδ

µν µν

mn mn

⎡

⎣

⎤

⎦

−

And so this becomes

22 2

XX xx

µν µν

µν

=−+

∑

CCln

zzz

nn−

′

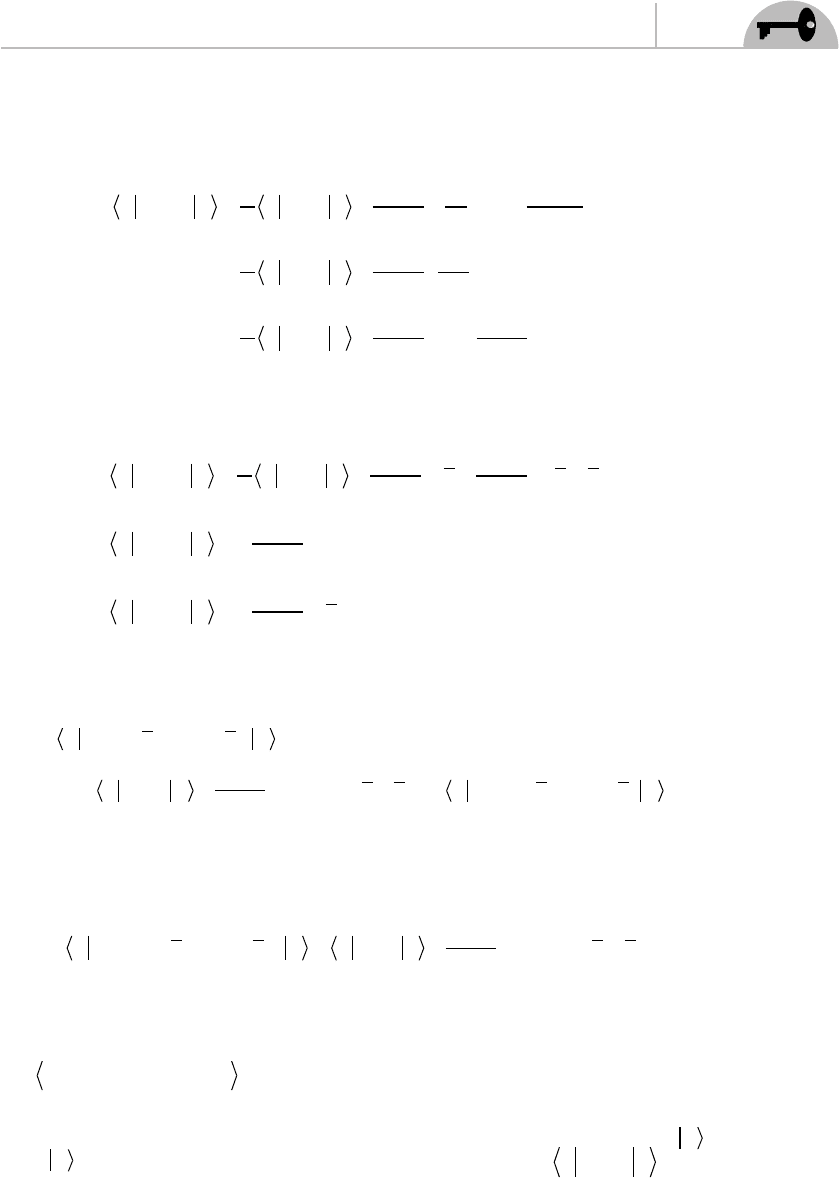
CHAPTER 5 Conformal Field Theory Part I

109

Now, using the fact that

xn x

/ln(

)

∞

∑

=− −

, we can write this as

XX xx

µν µν

µν

=−+

′

CC (/)

∑

=−+−

′

⎛

⎝

⎜

⎞

⎠

⎟

µν

C ln

ln( / )

xx z z z

µν

µν µν

ηη

+− −

′

ln ln( )

Similar calculations show that

XX xx z z z

µν µν

ηη

=+−−

′

ln ln( ))

XX z

µν

=−

XX z

µν

=−

Adding these terms up we ﬁ nd that

XzzXzz

xx z z

µν

(, ) ( , )

ln[(

′′

=−−

′

))( )] ( , ) ( , )zz XzzXzz−

′

′′

νµ

So the vacuum expectation value of the time ordered product is

0000

TX zzX z z xx z

[ ( , ) ( , )] ln[(

µν µν

µν

′′

=−

−−

′

−

′

zzz)( )]

Now let’s return to the two-point function:

XX TXX

µν µν

στ σ τ στ σ τ

(, ), ( , ) ( (, ), ( , )

′′

)): (,) ( , ):−

′′

µν

στ σ τ

Normal ordering puts all destruction operators to the right. So

::px

µν

0 =

νµ

00=

. Also, normal ordering of terms like

10 0

/( )mn z z

αα

µν

≠

−−

∑

′

110

String Theory Demystiﬁ ed

puts all destruction operators to the right annihilating the vacuum. So the vacuum

expectation value of the normal ordered piece reduces to

0000:(,)(,):XX xx

µν µν

στ σ τ

′′

Hence the two-point function is

XX TX X

µν µ ν

στ σ τ στ σ τ

( , ), ( , ) ( ( , ), ( , ))

′′

−−

′′

=− −

′

−

′

:(,)(,):

ln ( )(

zzz

µν

στ σ τ

zz zz

)

ln( ) ln( )

[]

=− −

′

−−

′

ηη

µν µν

Now that we have this expression, we can easily calculate other quantities that

involve derivatives, say. For example, to calculate the two-point function

∂

′′

Xzz Xzz

µν

(, ), ( , )

, we just differentiate the result:

∂

′′

=∂ − −

′

−

Xzz Xzz zz

µν

ηη

( , ), ( , ) ln( )

µµν

µν

ln( )−

′

⎡

⎣

⎢

⎤

⎦

⎥

=−

−

′

And

∂∂

′′

−

′

Xzz Xzz

µν

(, ), ( , )

()

Operator Product Expansion

A key concept we need to continue forward is known as an operator product

expansion. This is often given the abbreviation OPE. An operator product expansion

is a series expansion of a product of two operator-valued ﬁ elds. Let’s denote these

ﬁ elds by A

and consider two space-time points z and w. Then in a region R that does

not contain w

AzAw c z wA w

i j ijk k

() () ( ) ()=−

∑

(5.36)

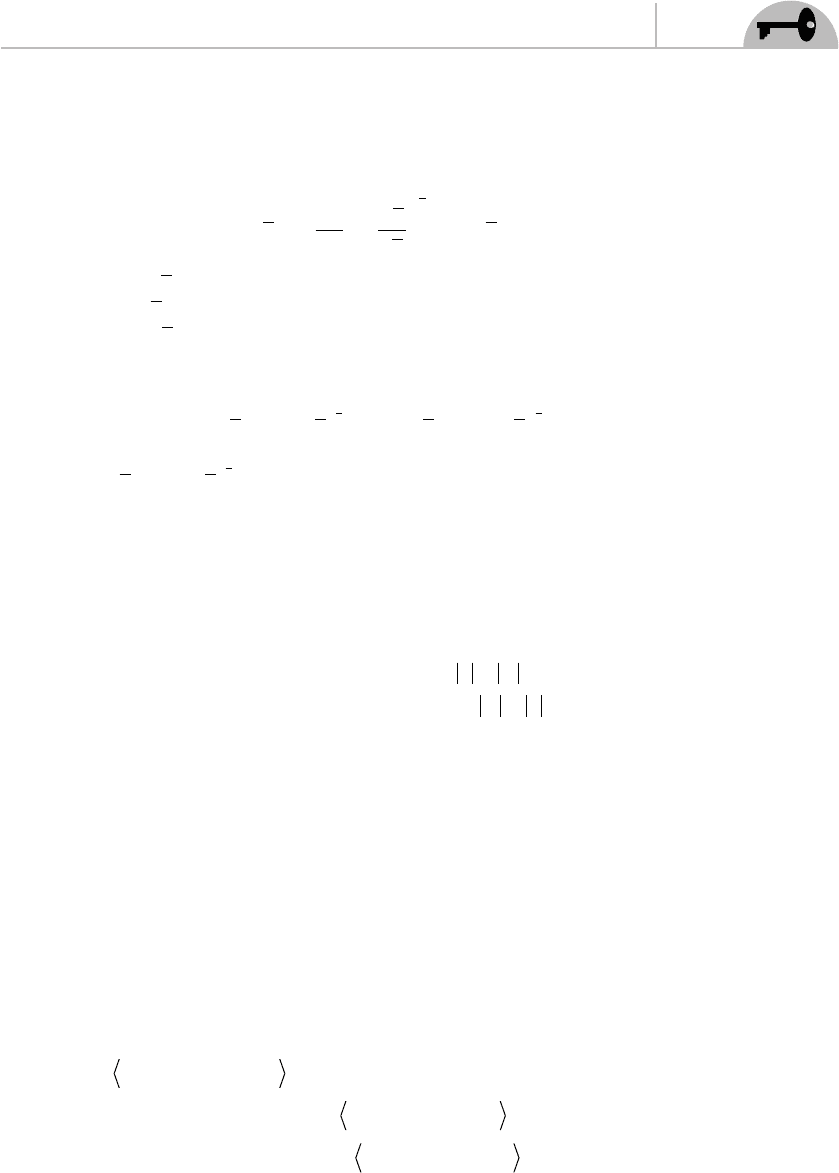
CHAPTER 5 Conformal Field Theory Part I

111

The

czw

()−

are analytic functions in R and the

()

are operator-valued

ﬁ elds. Now, deﬁ ne a conformal transformation

zwz→ (

)

. A conformal ﬁ eld or

primary ﬁ eld is one that transforms as

ΦΦ(, ) ( , )zz

∂

⎛

⎝

⎜

⎞

⎠

⎟

∂

⎛

⎝

⎜

⎞

⎠

⎟

(5.37)

We say that

(, )hh

are the conformal weights or conformal dimension of the ﬁ eld.

In particular,

is the dimension which describes how the ﬁ eld

behaves under

scaling, while

hh−

is the spin of

, which describes how the ﬁ eld is transformed

under a rotation. If Eq. (5.37) is satisﬁ ed, then it follows that

ΦΦ(,)()() (,)()()z z dz d z w w dw dw

hh hh

(5.38)

That is,

Φ(, )( )( )zz dz dz

is invariant under a conformal transformation.

Working in the complex plane, time ordering is transformed into radial ordering

because as we mentioned above, the radial direction encodes the ﬂ ow of time in the

z plane. Consider two operators deﬁ ned in the complex plane

zBw() ( ) and

. The

radial-ordering operator R ﬁ xes the order of the operators based on which one has

the larger radius in the complex plane. That is,

RAzBw

AzBw z w

Bw Az w z

[()()]

() ( ),

() ()(),

−>

⎧

⎨

⎩⎩

If the operators are fermionic, then

= 1

One operator product expansion of particular interest involves the energy-

momentum tensor. In the complex plane

Tz X X

zz z z

() : :=∂∂

µν

(5.39)

EXAMPLE 5.4

Find the operator product expansion of the radially ordered product

Tz Xw

() ( )∂

SOLUTION

Using Eq. (5.39) we have

RT z X w R X z X z X

zz w z z w

( ( ) ( )) (: ( ) ( ) : (∂=∂∂∂

µν

µν ρ

Xz Xw Xz

Xz X

zw z

))

() ( ) ()

()

=∂ ∂ ∂

+∂ ∂

µν

µρ ν

µν

ρρµ

() ()wXz

∂

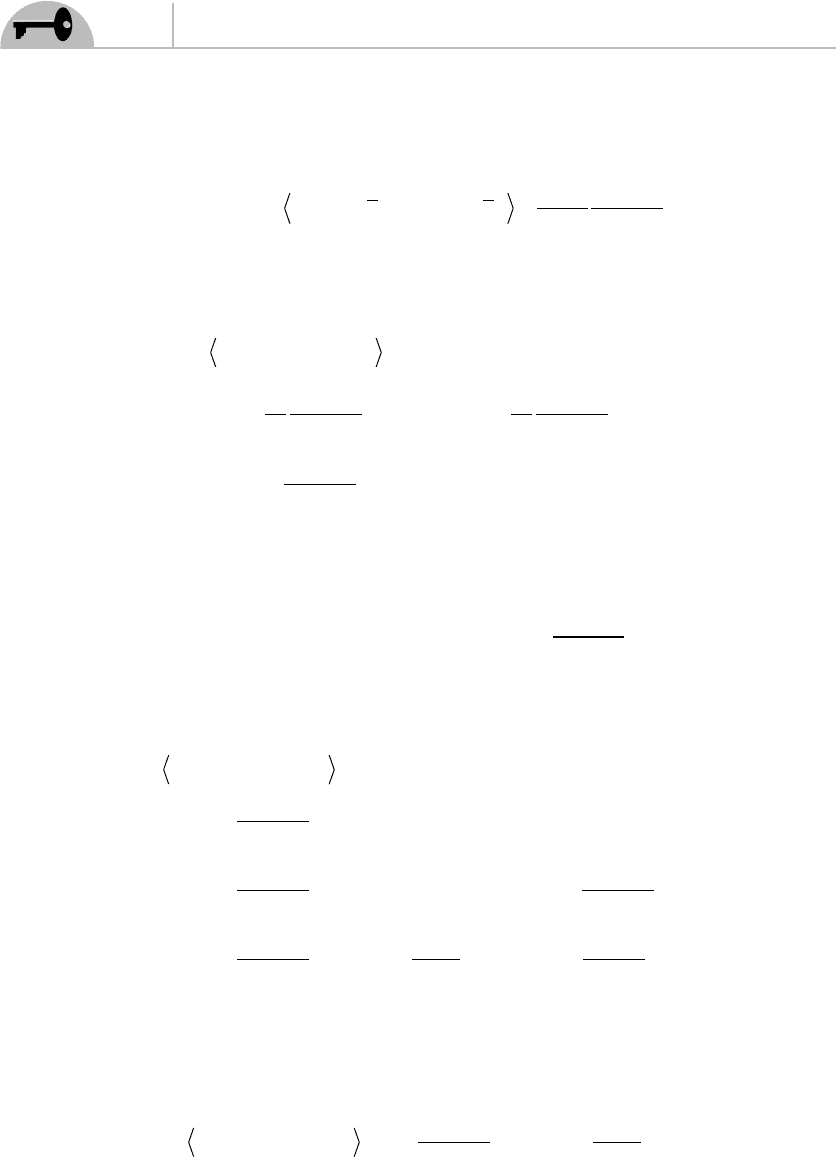
112

String Theory Demystiﬁ ed

Now we can use our previous result, namely

∂∂

′′

−

′

Xzz Xzz

µν

(, ), ( , )

()

And so we obtain

RT z X w

zz w

(() ())

()

∂

=−

−

∂−

µν

µρ ν

ηη

()

(

−

∂

=−

−

∂

ηη

µν

νρ µ

))

Now expand

∂

()

in a power series about the point

zw=

. We ﬁ nd

∂=∂ +−∂ +

−

∂

zw z z

Xz Xw zw Xz

ρρ ρ ρ

() ( ) ( ) ()

()

(()z +$

Hence

RT z X w

zz w

(() ())

()

(

∂

=−

−

∂

=−

−−

∂+−∂+

−

∂

Xw zw Xz

wz z

)

() ( ) ()

()

ρρ ρ

⎧

⎨

⎩

⎫

⎬

⎭

=−

−

∂−

−

∂

()

() ()

ρρ

−−

−

∂+C$

()

The singular terms are what is of interest. So it is typical to use an ellipsis

represent the regular terms in the summation and write

RT z X w

zz w s w

(() ())

()

()∂=−

−

∂−

−

∂

ρρ

()+$

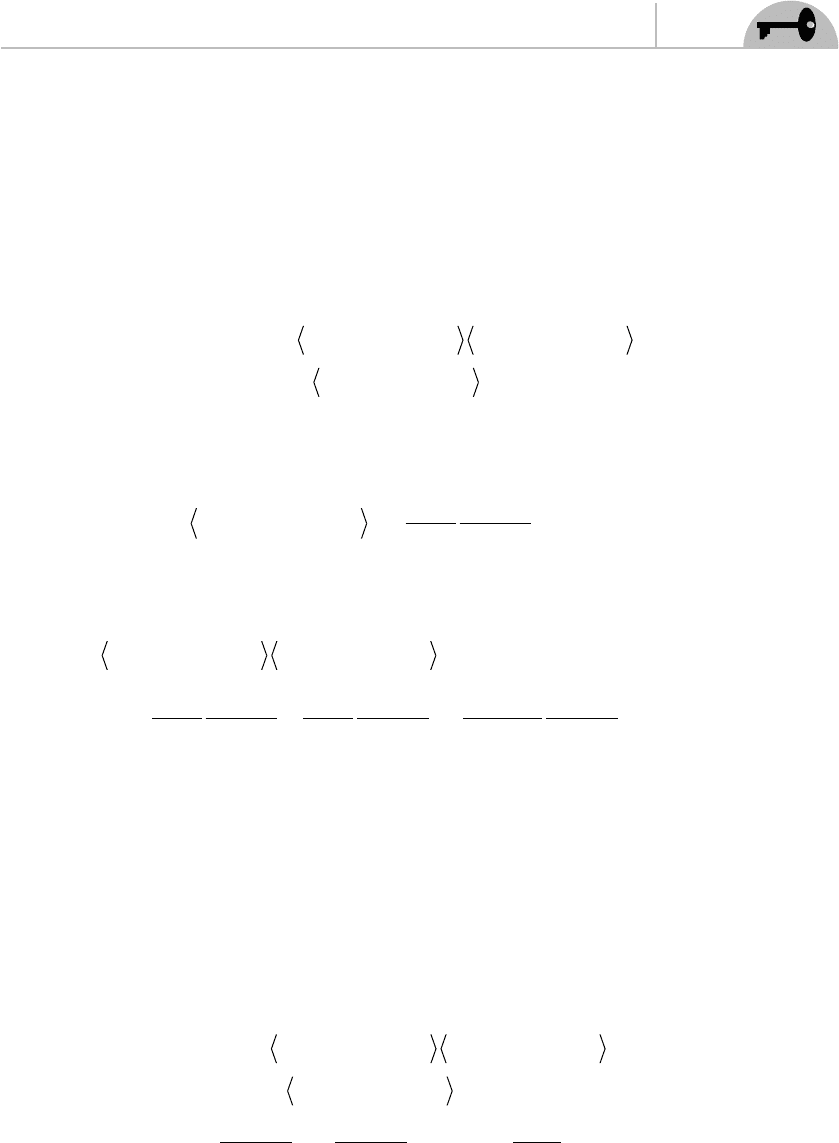
CHAPTER 5 Conformal Field Theory Part I

113

EXAMPLE 5.5

In this example we compute an important result, the OPE of

TzT w

zz ww

() ( )

SOLUTION

Using radial ordering we have

RT zT w R X z X z

zz ww z z w

( () ( )) ( : () (): :=∂∂ ∂

ηη

µν

ρσ

XXw Xw

Xz Xw Xz

zw z

ρσ

µν ρσ

µρ ν

ηη

() ())

() ( ) ()

∂

=∂∂∂2

∂∂

+∂∂ ∂∂

zw zw

Xz Xw Xz X

µν ρσ

µρ νσ

ηη

()

() ( ): () (4 ww):

We have already seen that

∂∂ =−

−

Xz Xw

µρ

(), ( )

()

Hence

∂∂ ∂∂

−

zw zw

Xz Xw Xz Xw

µρ νσ

µρ

() ( ) () ( )

()

⎛⎛

⎝

⎜

⎞

⎠

⎟

−

⎛

⎝

⎜

⎞

⎠

⎟

−

ηηη

νσ µρ νσ

zw zw

() ())

Now the metric terms give us the dimension of the space:

ηηηη δδ

µν ρσ

µρ νσ

==D

In the last term of

RT zT w

zz ww

(() ())

which includes the normal ordered product,

we expand

∂

()

about w the way we did in Example 5.4. Then we obtain the

operator product expansion for the energy-momentum tensor:

RT zT w X z X w X z

zz ww z w z

(() ()) () () (=∂∂∂2

ηη

µν ρσ

µρ ν

))()

() ( ): ()

∂

+∂∂ ∂

zw z

Xz Xw Xz

µν ρσ

µρ ν

ηη

4 ∂∂

−

sswws

zw zw

():

() ()

()CC C

22 11

www

−

∂+()$

114

String Theory Demystiﬁ ed

Summary

Conformal ﬁ eld theory is a tool that allows us to transform the physics of the string

worldsheet to the complex plane. Calculations are much easier to do using the

techniques of complex variables. In this chapter we introduced some of the basic

terminology and techniques. In the following chapters, we will continue our

exploration of conformal ﬁ eld theory in the context of string theory by exploring

Kac-Moody algebras, minimal models, vertex operators, and BRST quantization.

Quiz

1. Calculate

[,]CC

2. Does

()=

satisfy the group composition property?

3. Consider

()=

with a pure imaginary. Find the generator of the

transformation.

4. Following the text, calculate

00XX

µν

5. For a closed string, calculate

∂∂

′′

′

Xzz Xzz

µν

(, ), ( , )

6. Calculate

00:(,)(,):XzzXzz

µν

′′

7. Find

00XzzXzz

µν

(, ) ( , )

′′

8. By exploiting the properties of the natural logarithm function, and using

the fact that

0000XzzXzz XzzXzz

µν ν µ

(, ) ( , ) ( , ) (, )

′′

, ﬁ nd a

compact expression for

00XzzXzz

µν

(, ) ( , )

′′

9. Find the operator product expansion of

RT z e

ik X w

((): :)

()⋅

CHAPTER 6

BRST Quantization

So far we have seen two methods that can be utilized to quantize the string: the

covariant approach and light-cone quantization. Each offers its advantages.

Covariant quantization makes Lorentz invariance manifest but allows for the

existence of “ghost states” (states with negative norm) in the theory. In contrast,

light-cone quantization is ghost free. However, Lorentz invariance is no longer

obvious. Another trade-off is that the proof of the number of space-time dimensions

(D = 26 for the bosonic theory) is rather difﬁ cult in covariant quantization, but it’s

rather straightforward in light-cone quantization. Finally identifying the physical

states is easier in the light-cone approach.

Another method of quantization, that in some ways is a more advanced approach,

is called BRST quantization. This approach takes a middle ground between the two

methods outlined above. BRST quantization is manifestly Lorentz invariant, but

includes ghost states in the theory. Despite this, BRST quantization makes it easier

to identify the physical states of the theory and to extract the number of space-time

dimensions relatively easily.