McMahon D. String Theory Demystified
Подождите немного. Документ загружается.


36
String Theory Demystifi ed
The Polyakov Action
Quantization using the Nambu-Goto action is not convenient due to the presence of
the square root in the lagrangian. It is possible to write down an equivalent action,
equivalent in the sense that it leads to the same equations of motion—that does not
have the cumbersome square root. This action goes by the name of the Polyakov
action or by the more modern term the string sigma model action.
Look back to the start of the chapter when we considered the point particle. There
too, we ran into a situation where the action had a square root and we dealt with it by
introducing an auxiliary fi eld
a()
τ
. We can use the same procedure here, to rewrite the
action for the string in a more convenient form. This is done by introducing an intrinsic
metric
h
αβ
τσ
(, )
, which acts like the auxiliary fi eld. We use the notation
h
αβ
because
the metric can be written as a matrix. We use the indices to denote rows and columns in
this matrix. Then, using the notation
hh= det
α
β
, the Polyakov action can be written as
S
T
dhhXX
P
=− − ∂ ∂
∫
2
2
ση
αβ
α
µ
β
ν
µν
(2.27)
A historical aside: While Polyakov did important work with this action, it was
actually proposed by Brink, Di Vecchia, and Howe and independently by Desser
and Zumino. Polyakov got his name attached to it by using it in a path integral
quantization of the string. It is also called the string sigma action.
Mathematical Aside: The Euler Characteristic
The Euler characteristic
χ
is a number which describes the shape of a topological
space. Consider a polyhedron, and let V be the number of vertices, E be the number
of edges, and F be the number of faces. Then the Euler characteristic is
χ
=−+VEF
(2.28)
In string theory, we often want to know whether or not two geometric shapes or
topologies are similar to one another in a specifi c way. In particular, we want to
know if we can continuously deform one shape into another (imagine working with
clay and deforming one shape into another without breaking the clay apart, or
introducing or losing any holes). Formally, a homeomorphism is a deformation of a
geometric object into a new shape by stretching or compressing and being it, without
tearing or breaking it. For instance, the quintessential example is a donut and a
coffee cup (conveniently paired for police offi cers). You could use a continuous
deformation to transform one into the other or vice versa. So we say that a coffee
cup and a donut are homeomorphic. On the other hand, a sphere and a donut are not

CHAPTER 2 Equations of Motion
37
homomorphic—the donut has a hole but a sphere does not. The bottom line is there
is no way to transform the donut into the sphere.
If a geometric shape is homeomorphic to a sphere, then the Euler characteristic is
χ
=−+=VEF2
(2.29)
Many shapes have an Euler characteristic which vanishes. Some examples of this
include a torus, a möbius strip, and a Klein bottle. Another example is a cylinder,
which also has
χ
= 0
(see Fig. 2.2). Why is this interesting for us? If the worldsheet
of a string has a vanishing Euler characteristic, then it is possible to write the
auxiliary fi eld
h
αβ
as a two-dimensional fl at space metric. That is, we take [using
the choice of coordinates for the worldsheet as
(, )
τσ
]
h
αβ
=
−
⎛
⎝
⎜
⎞
⎠
⎟
10
01
(2.30)
Klein bottle
Tours
Mobius strip
C
y
linder
Figure 2.2 Some surfaces with a vanishing Euler characteristic. When the Euler
characteristic vanishes, we can defi ne the auxiliary fi eld such that it has
a representation of the fl at space Minkowski metric.
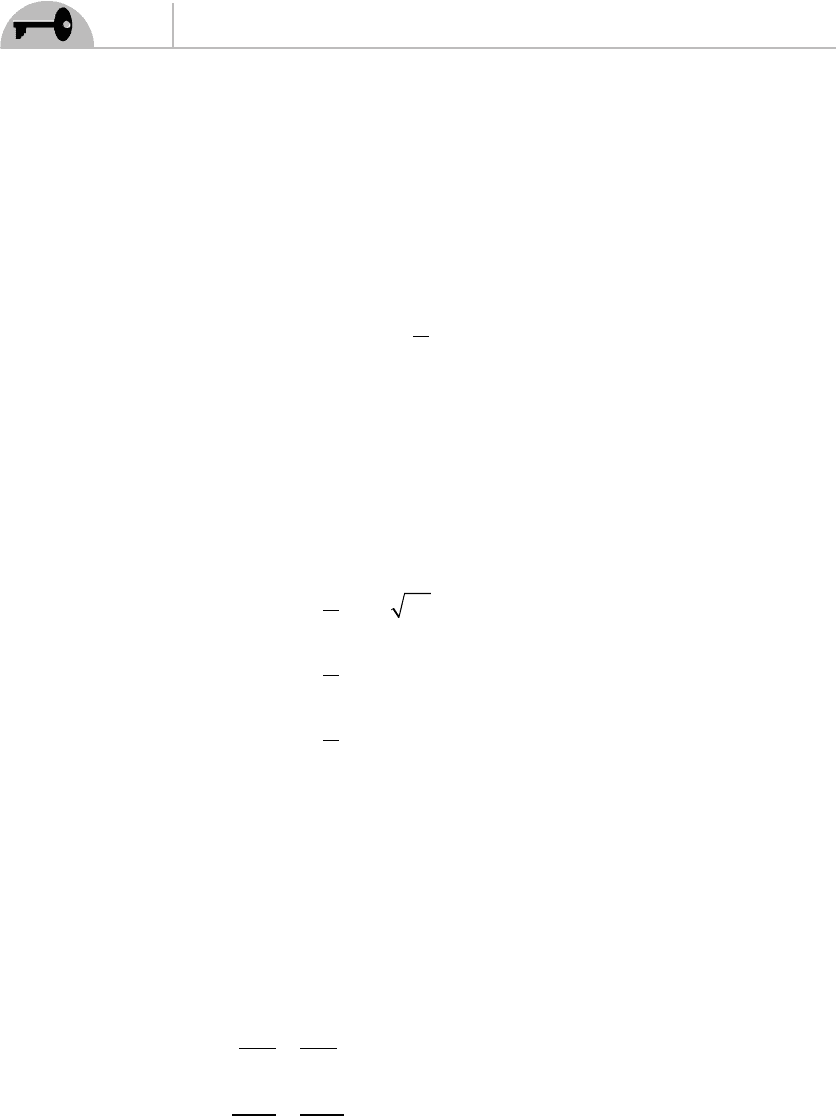
38
String Theory Demystifi ed
Now notice that with this choice,
hh==−det
αβ
1
. We also have
hXX XX XXXX
αβ
αβ ττ σσ
∂ ⋅∂ =−∂ ⋅∂ +∂ ⋅∂ =− +
′
22
In this case, we are able to write the Polyakov action in the remarkably simple
form
S
T
dXX
P
=−
′
∫
2
22 2
σ
()
(2.31)
EXAMPLE 2.3
Find the equations of motion using the Polyakov action as written in Eq. (2.27)
when the auxiliary fi eld takes the form of the fl at space metric.
SOLUTION
In this case we have
S
T
dhhXX
T
dXX
P
=− − ∂ ∂
=− −∂ ⋅∂
∫
∫
2
2
2
2
ση
σ
αβ
α
µ
β
ν
µν
ττ
( ++∂ ⋅∂
=− − ∂ ∂ + ∂ ∂
∫
σσ
µν τ
µ
τ
ν
µν σ
µ
σ
ν
ση η
XX
T
dXXXX
)
(
2
2
))
So, we can write the lagrangian as
LXXXX
XX X
=− ∂ ∂ + ∂ ∂
=− +
′
ηη
ηη
µν τ
µ
τ
ν
µν σ
µ
σ
ν
µν
µν
µν
µµν
′
X
Therefore,
∂
∂
=
∂
∂
−+
′′
()
=− =
L
XX
XX X X X
µµ
µν
µν
µν
µν
µν
ν
ηη η
−−
∂
∂
′
=
∂
∂
′
−+
′′
()
=
X
L
XX
XX X X
µ
µµ
µν
µν
µν
µν
µν
ηη η
′′
=
′
XX
ν
µ

CHAPTER 2 Equations of Motion
39
The Euler-Lagrange equations are
∂
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
+∂
∂
∂
′
⎛
⎝
⎜
⎞
⎠
⎟
=
τ
µ
σ
µ
L
X
L
X
0
(2.32)
Hence, we fi nd that the equations of motion for the relativistic string are
∂
∂
−
∂
∂
=
2
2
2
2
0
XX
µµ
τσ
(2.33)
It will be convenient to call upon light-cone coordinates in string theory. First, let’s
look at how light-cone coordinates can be defi ned in Minkowski space-time in
general and then consider having them in the context of the worldsheet and the
equations of motion of the string. As we will see, this will simplify the way we
write the action and the resulting equations of motion.
For simplicity, let’s take ordinary (3 + 1) dimensional space-time. The contravariant
coordinates are
xxxxx
µ
= (,,,)
0123
where
xct
0
=
and
xxx yxz
123
===,,
say. We form light-cone coordinates by
choosing one spatial direction, which in this case we take to be x
1
, and forming
linear combinations of it with x
0
as follows:
x
xx
x
xx
+−
=
+
=
−
01 01
22
(2.34)
These are two null or lightlike coordinates, but you can think of x
+
as a timelike
coordinate and x
–
as a spacelike coordinate. Hence when we use indices and
summations, we will treat + as a “0” index and – as a “1” index. The other
coordinates x
2
and x
3
are left alone.
It is easy to derive the inverse relationship using Eq. (2.34). We have
x
xx
x
xx
01
22
=
+
=
−
+− +−
Light-Cone Coordinates

40
String Theory Demystifi ed
Using the Minkowski metric, we have seen that infi nitesimal distances in space-
time can be defi ned according to
ds dx dx dx dx dx dx
2021222
=− =−−−
η
µν
µν
()()()(
332
)
Since,
dx
dx dx
dx
dx dx
01
22
=
+
=
−
+− +−
(2.35)
we can rewrite
ds
2
in terms of light-cone coordinates as
ds dx dx dx dx
22232
2=−−
+−
()()
(2.36)
So, we can defi ne distances in terms of a light-cone Minkowski metric
ˆ
η
µν
=
−
−
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
0100
1000
0010
0001
(2.37)
Using Eq. (2.37), distances can be written compactly as
ds dx dx
2
=−
ˆ
η
µν
µν
(2.38)
Working with vectors is a simple extension of what we’ve written for coordinates.
That is, defi ne light-cone components of a vector
v
µ
as
v
vv
v
vv
+−
=
+
=
−
01 01
22
(2.39)
Using the metric from Eq. (2.37) the inner product between two vectors can be
calculated as
vw vw vw vw vw vw
ii
i
⋅= = =− − +
+− −+
∑
ˆ
η
µν
µν µ
µ
(2.40)

CHAPTER 2 Equations of Motion
41
where generally,
id=−11,,…
. We can apply index raising and lowering to the
light-cone components of vectors using a sign change
vv vv
+
−
−
+
=− =−
The other components of the vector are left unchanged, that is,
vv
i
i
=
.
Now that we’ve seen how to defi ne light-cone coordinates for space-time, let’s
see how to defi ne them for the worldsheet and hence for the string. In this case, we
defi ne
στσ στσ
+−
=+ =−
(2.41)
Now since
ddd
στσ
+
=+
and
ddd
στσ
−
=−
, it should be clear that
ds d d
2
=−
+−
σσ
(2.42)
This tells us that we can write the induced metric in Eq. (2.30) indexing a matrix as
(,,,)+++−−+−−
giving
h
αβ
=
−
−
⎛
⎝
⎜
⎞
⎠
⎟
012
12 0
/
/
(2.43)
You can quickly verify that the determinant is
hh==−det /
αβ
1
4
and the inverse of
Eq. (2.43) is
h
αβ
=
−
−
⎛
⎝
⎜
⎞
⎠
⎟
02
20
A relationship can also be written down between the derivatives with respect to the
coordinates
τσ
,
and the light-cone coordinates. For notational convenience, we
use the relativistic shorthand notation for derivatives
∂=
∂
∂
i
i
x
and write
∂= ∂+∂ ∂= ∂−∂
+−
1
2
1
2
() ()
τσ τσ
(2.44)

42
String Theory Demystifi ed
Let’s see how the action for the string is written using light-cone coordinates.
The Polyakov action, which we reproduce here for your convenience, is
S
T
dhhXX
P
=− − ∂ ∂
∫
2
2
ση
αβ
α
µ
β
ν
µν
Using Eq. (2.43), we fi nd that
−∂∂ =− ∂∂ − ∂
+−
+−
−+
hh X X h X X h
αβ
α
µ
β
ν
µν
µν
µν
ηη
14 14//
−−+
+−
∂
=− ∂ ∂
XX
XX
µν
µν
µν
µν
η
η
2
Hence, using light-cone coordinates we fi nd the Polyakov action can be written as
STd XX
P
=∂∂
∫
+−
2
ση
µν
µν
(2.45)
We can fi nd the equations of motion by varying S
P
. We have
δδ σ η
σδ η
µν
µν
µν
µν
STd XX
Td X X
T
P
=∂∂
=∂∂
=
∫
∫
+−
+−
2
2
()
ddXXTdXX
22
σδ η σ δ η
µν
µν
µν
µν
∫∫
∂∂ + ∂ ∂
+− + −
() ()
The following fact helps us proceed:
δ
σ
δ
σ
µµ
∂
∂
=
∂
∂
±±
XX()
Therefore,
δσδησδη
µν
µν
µν
µν
STd X X Td X X
P
=∂∂+∂∂
+− +−
∫∫
22
() ()
Now integrate by parts to move the derivative away from the
δ
µ
X
term. Remember
that
udv uv vdu
∫∫
=−

CHAPTER 2 Equations of Motion
43
In our case, we get
δσδησδη
µν
µν
µν
µ
STd X X Td XX
P
=− ∂ ∂ − ∂ ∂
∫∫
+− −+
22
() ()
νν
We’ve dropped the boundary terms, which must vanish for Neumann boundary
conditions in the case of open strings or for the requirement of periodicity for closed
strings. Since
δ
µ
X
is arbitrary and
δ
S
P
=
0
, it must be the case that
∂∂ =
+−
X
µ
0
(2.46)
This is the wave equation for relativistic strings using light-cone coordinates.
In the next chapter, we will consider the hamiltonian and stress-energy tensor and
write down conserved charges and currents for the string. Right now, let’s focus on
fi nding a solution of the wave equation given in Eq. (2.46).
From elementary mechanics, we know that the solution of a wave equation can
be written in terms of a superposition of waves moving to the left on the string and
waves moving to the right on the string. If the motion is in one dimension (call it x),
then we can write down a solution of the form
ftx fxvt fxvt
LR
(, ) ( ) ( )=−++
We will write the equations of motion for the relativistic string in the same way.
We have a solution which is a superposition of left-moving components
X
L
µ
τσ
()+
and right-moving components
X
R
µ
τσ
(
)
−
:
XX X
LR
µµ µ
τσ τσ τσ
(, ) ( ) ( )=++−
(2.47)
You should recall from partial differential equations that the most general solution
can be written as an expansion of Fourier modes. Here, we denote these modes as
α
µ
k
, and write the left-moving and right-moving components as
X
x
pi
k
e
L
ssk
ik
µ
µ
µ
µ
τ
τσ τ σ
α
(, ) ( )
(
=+ ++
−+
22
2
2
CC
σσ
)
k≠
∑
0
(2.48)
X
x
pi
k
e
R
ssk
ik
µ
µ
µ
µ
τσ τ σ
α
(, ) ( )
(
=+ −+
−
22
2
2
CC
ττσ
−
≠
∑
)
k 0
(2.49)
Solutions of the Wave Equation

44
String Theory Demystifi ed
We have introduced some new terms here. First, we have included the
characteristic length of the string which is related to the Regge slope parameter
′
α
and hence to the tension in the string via
T
s
=
′
=
′
1
2
1
2
2
πα
α
C
(2.50)
Next, notice the coordinate
x
µ
and momentum
p
µ
. These are the center of mass
coordinate and the total momentum of the string, respectively. The “zeroth”-order
Fourier mode is defi ned in terms of
αα
µµµµ
00
22
==
CC
ss
pp
(2.51)
What does this tell us physically? The solutions imply that the string can move as a
single unit with position and momentum through space-time. In addition, it also has
vibrations, which are described by the modes
α
µ
k
. When you see modes like this,
you should think quantization (think in terms of the harmonic oscillator or fi elds in
quantum fi eld theory).
Remember, we are still in the realm of classical physics, even if it’s relativistic
classical physics. So the solutions of the wave equation
XX X
LR
µµ
µ
,,and
must be
real functions. This implies that
x
µ
and
p
µ
are real (as they must be, given their
physical interpretation) and allows us to relate positive and negative modes
αα αα
µµ µµ
−−
=
(
)
=
(
)
kk kk
**
(2.52)
where * represents the complex conjugate. Now, let’s take a look at the solutions of
the wave equation with different boundary conditions.
Open Strings with Free Endpoints
Open strings with free endpoints satisfy the Neumann boundary condition that we
reproduce here:
∂
∂
==
X
µ
σ
σπ
00when ,

CHAPTER 2 Equations of Motion
45
Now, looking at Eqs. (2.48) and (2.49) we see that
∂
∂
=+
−+
≠
∑
X
pe
L
ss
k
ik
k
µ
µµτσ
σ
α
CC
2
0
2
2
()
∂
∂
=− −
−+
≠
∑
X
pe
R
ss
k
ik
k
µ
µµτσ
σ
α
CC
2
0
2
2
()
Summing these as in Eq. (2.47) and setting
σ
= 0
,
∂
∂
=
⇒= − + −
()
−
≠
∑
X
pp e
ss
kk
ik
k
µ
µµ µµ τ
σ
αα
0
0
2
2
2
0
CC
()
This tells us that in the case of an open string with free endpoints, it must be the
case that
pp
k
µµ
µ
α
=
=
()string cannot wind around itself
αα
µ
k
(same modes for left- and right-moving wwaves)
Physically, this means that for an open string with free endpoints the modes
combine to form standing waves on the string. Before we move on to our next case,
let’s consider the other boundary condition, which is imposed at the other end of the
string
σπ
=
.
0
2
2
2
=
∂
∂
+
∂
∂
=+
==
−+
XX
pe
LR
ss
k
ik
µ
σπ
µ
σπ
µµτπ
σσ
α
CC
( ))()
k
ss
k
ik
k
s
k
i
pe
e
≠
−+
≠
−
∑∑
−−
=
0
2
0
2
2
2
CC
C
µµτπ
µ
α
α
kk
ik ik
k
sk
ik
ee
i
i
ie
τ
ππ
µτ
α
−
≠
−
−
⎛
⎝
⎜
⎞
⎠
⎟
=
∑
2
2
2
0
()
sC iin( )k
k
π
≠
∑
0
