Mattingly J.D., Heiser W.H., Pratt D.T. Aircraft Engine Design
Подождите немного. Документ загружается.

40 AIRCRAFT ENGINE DESIGN
Cruise
3=0.81
fl
=
0.73
Loiter fl =
0.95
I Descend F
~=o.~ ~=1
and Takeoff
Cruise
Climb
fl = 0.86 ~I~
Descend
and Takeoff
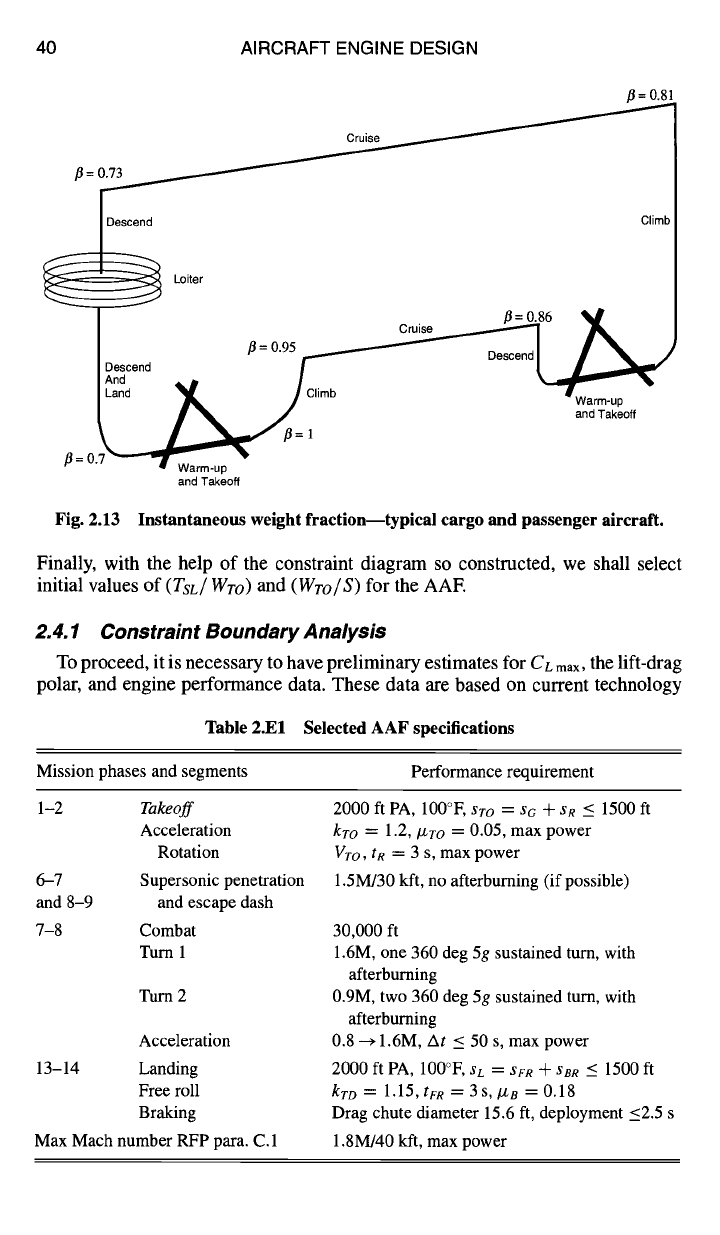
Fig. 2.13 Instantaneous weight fraction--typical cargo and passenger aircraft.
Finally, with the help of the constraint diagram so constructed, we shall select
initial values of
(TsL/Wro)
and
(Wro/S)
for the AAE
2.4.1 Constraint Boundary Analysis
To proceed, it is necessary to have preliminary estimates for CL max, the lift-drag
polar, and engine performance data. These data are based on current technology
Table 2.El Selected AAF specifications
Mission phases and segments Performance requirement
1-2 Takeoff
Acceleration
Rotation
6-7 Supersonic penetration
and 8-9 and escape dash
7-8 Combat
Turn 1
Turn2
Acceleration
13-14 Landing
Free roll
Braking
Max Mach number RFP para. C. 1
2000 ft PA, 100°E
STo
=
S G ~-
S R
<_<
1500 ft
kTo = 1.2, #tO
= 0.05, max power
Vro,
tR = 3 s, max power
1.5M/30 kft, no afterburning (if possible)
30,000 ft
1.6M, one 360 deg 5g sustained turn, with
afterburning
0.9M, two 360 deg 5g sustained turn, with
afterburning
0.8 -+ 1.6M, At < 50 s, max power
2000 ft PA, 100°F, SL =
SIR + SBR <
1500 ft
krD
= 1.15,
tFR
= 3 S, /ZB = 0.18
Drag chute diameter 15.6 ft, deployment <2.5 s
1.8M/40 kft, max power

CONSTRAINT ANALYSIS 41
for fighter-type aircraft and engines. The variation of thrust with Mach number
and density is shown in Fig. 2.Elb that depicts the so-called engine thrust lapse
of Eqs. (2.54a) and (2.54b) for three typical values of the throttle ratio
(TR).
In
addition, the instantaneous weight fraction (fl) must be estimated for each item of
Table 2.El. Reasonable estimates (see Figs. 2.12 and 2.13) will fall between 1.0
at takeoff and 0.5, say, at landing.
The aerodynamic data of Fig. 2.El a provide the initial estimates of CL
max, K1,
and
CDO
required by Eq. (2.1 lb) and its descendants. Please note that the AAF is at
first assumed to have an uncambered airfoil, for which K2 = 0. The following AAF
calculations will therefore use the relevant equations with K2 set equal to zero.
Note that CL max
=
2 was arrived at after many values of CL
max
were examined,
such that takeoff would not overconstrain the problem. According to Table 2.1, this
requires a fighter with very low wing sweep (improbable, especially in this case
with supercruise requirements) or augmented high lift (such as achieved by using
vortex lift created by leading edge extensions, etc.). This challenges the aircraft
designer to join in the effort by using advanced technology for this requirement.
The installed propulsion data of a low bypass ratio, mixed flow turbofan engine
are selected and plotted in Fig. 2.E lb based on Eqs. (2.54a) and (2.54b). A range of
TR
from 1.0 to 1.08 is shown because the hot day takeoff and supercruise require-
ments desire a
TR
greater than 1.0 (see Appendix D). It is important to have a
good first estimate of the installed engine thrust lapse, which is usually obtained
from such open literature information as company brochures, technical papers,
and textbooks. 1,2 Another very effective method for obtaining engine thrust lapse
is simply to run the performance computer portion of the AEDsys program sup-
plied with this textbook for an initial guess of the engine design point. That was
the origin of the engine thrust lapse equations of Sec. 2.3.2.
The computations and data required to construct each boundary in the complete
constraint diagram of the AAF are contained in the Sec. 2.4.3. The Constraint
Analysis software in the AEDsys program makes these calculations effortless.
Before determining the constraint for each item of Table 2.El in detail, we will
first illustrate the procedure with the takeoff distance and supercruise phases. This
will also help us appreciate the role of the engine
TR
and select a value capable of
meeting these two constraints.
Takeoff.
For this illustrative case we consider the airplane accelerated by
thrust with no resisting forces whatever in the ground roll. The thrust is balanced
by drag forces during the constant velocity rotation. Under these conditions our
takeoff constraint boundary equation comes from Case 5, Eq. (2.22), solved for
SG,
and Eq. (2.26), where
sTO = SG + SR,
or
STO ~--- [ pgofLmaxOlwet(ZsL/WTO) ] I VRCL max
(2.El)
which is in the form
a +b v

a)
0.40
0.35
0.30
0.25
K1
0.20
0.15
0.10
0.05
0.00
b)
1.4
T
h 1.2
r
u
s 1.0
t
0.8
L
a
P 0.6
S
e
0.4
0.2
0.0
2
C D = K1C L
+Coo,
CLmax
= 2.0
I ' ' ' ' r ' ' ' '
C~o...~ /
./
___ /~ "'~'XK 1
I i n t n I i
= n
I
0.5 1.0 1.5
Mach Number
/
u
TR = 1.08
1.05
/_
Max../ ...... - -.. \
j -. \
1.00 ",
"%
\
, \
40 kft
Max
Mil
/
s
TR = 1.08
1
0.040
,,: 0.035
0.030
0.025
0.020
0.015
0.010
0.005
0.000
2.0
1.05
Coo
.0 " "
0.0 0.50 1.0 1.5 2.0
Mach Number
Fig. 2.El Preliminary AAF data: a) aerodynamic data; b) installed thrust lapse.
42

CONSTRAINT ANALYSIS 43
Table 2.E2 Thrust lapse variation
with throttle ratio-AB on
TR ~)lwe t
1.00 0.6885
1.05 0.8400
1.06 0.8703
1.07 0.9006
1.08 0.9309
From item 1 of Table 2.El, Fig. 2.E 1, and the standard atmosphere of Appendix
B, we have
kro = 1.2 /3 = 1.0 0 = 1.0796
MT'o = 0.1 CLmax = 2.0 8 = 0.9298
cr =8/0=0.8612 p=0.002047sl/ft 3 tR=3.0s
go = 32.17 ft/s 2
For the range of TR the corresponding thrust lapses (or) from Eq. (Z54a) are shown
in Table 2.E2.
With these values we can evaluate the coefficients a, b, and c in Eq. (2.El),
which, for computational convenience, we solve for WT.o/S in order to obtain
where
(--~)={-b+~} 22a
10.93
a= b-----79.57 c=1500
Otwet( TsL/ WTO )
whence we obtain the matrix of results for Wro/S:
(00)M=0.1 =
1.0818
(80)M=0.1 = 0.9363
STO = 1500ft
(2.E2)
TR TsL/Wro 0.4 0.8 1.2 1.6 2.0 2.4
1.00 Wro/S (lbf/ft 2) 27.3 47.9 64.9 79.6 92.5 104
1.05 Wro/S (lbf/ft 2) 32.2 55.7 74.8 91.1 105 118
1.06 Wro/S (lbf/ft z) 33.2 57.2 76.7 93.2 107 120
1.07 Wro/S (lbf/ft 2) 34.1 58.7 78.6 95.33 110 122
1.08 Wro/S(lbf/ft 2) 35.1 60.2 80.4 97.4 112 125
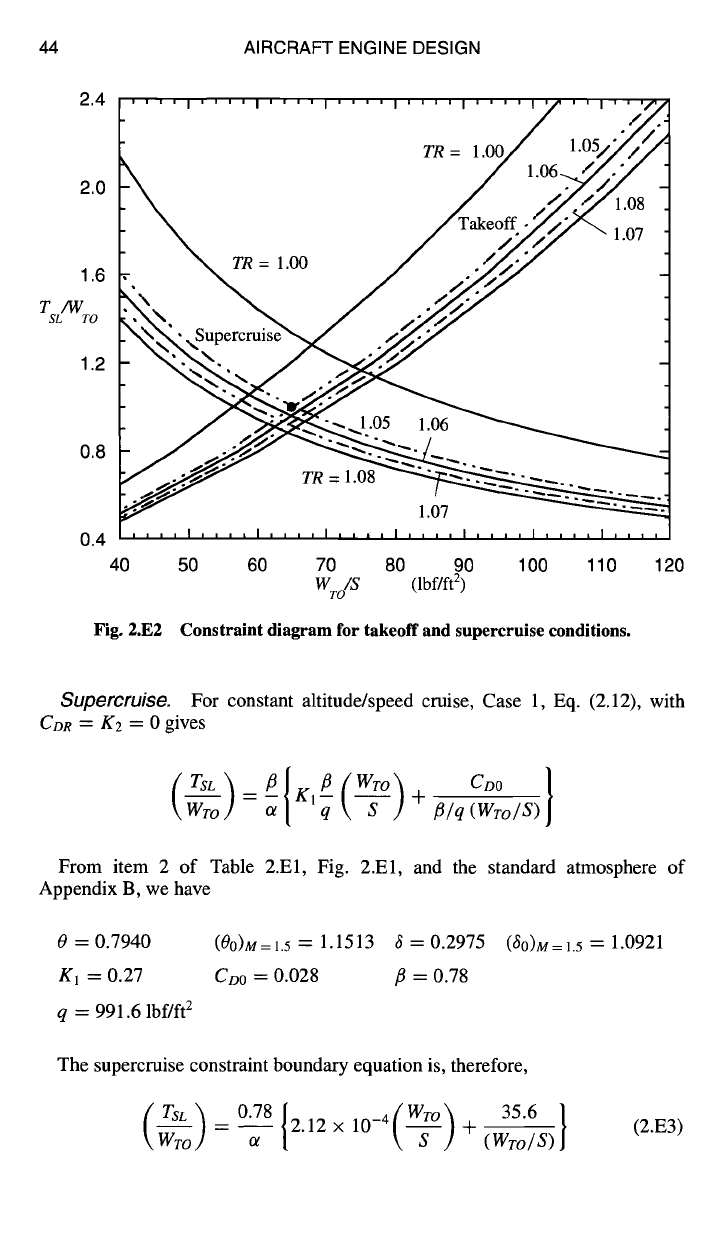
The takeoff constraint boundaries for this range of throttle ratios are shown in
Fig. 2.E2. An airplane with thrust and wing loadings in the region to the left of
the boundary can take off within the specified constraints, but those to the right
cannot.
44
2.4
AIRCRAFT ENGINE DESIGN
2.0
1.6
T/W
SL TO
1.2
0.8
0.4
40 50 60 70 80 90 100 110 120
W /S
(lbf/ft 2)
TO
Fig. 2.E2
Constraint diagram for takeoff and supercruise conditions.
Supercruise.
For constant altitude/speed cruise, Case 1, Eq. (2.12), with
CoR
= K2 = 0 gives
W~ro ,] Klq +
Coo }
fl /q (Wro/ S)
From item 2 of Table 2.El, Fig. 2.El, and the standard atmosphere of
Appendix B, we have
0 = 0.7940 (0o)M=1.5 = 1.1513 3 = 0.2975
K1 = 0.27
Coo
= 0.028 /~ = 0.78
q = 991.6 lbf/ft 2
(6o)M=1.5 = 1.0921
The supercruise constraint boundary equation is, therefore,
\~oro] ( TsL ~
0.78ot 2.12 x 10 .4
+ (Wro/S)I
(2.E3)

CONSTRAINT ANALYSIS 45
Table 2.E3 Thrust lapse variation
with throttle ratio-AB off
TR ado,
1.00 0.3278
1.05 0.4359
1.06 0.4576
1.07 0.4792
1.08 0.5008
with a = t~dry as a function of TR from
whence we obtain the matrix of results for TsL/Wro:
TR Wro/S (lbf/ft 2) 20 40 60
1.00 TsL/Wro 4.25 2.14 1.44
1.05 TsL/Wro 3.19 1.61 1.08
1.06 Tsl./Wro 3.04 1.53 1.03
1.07 TsL/Wro 2.90 1.46 0.986
1.08 TsJ Wro 2.80 1.40 0.944
Eq. (2.54b), as shown in Table 2.E3,
80 100 120
1.10 0.898 0.767
0.827 0.675 0.576
0.788 0.643 0.549
0.752 0.614 0.524
0.720 0.588 0.502
As shown in Fig. 2.E2, this constraint boundary places a lower limit on the
allowable wing loading and, together with the takeoff constraint boundary, encloses
the "solution space" of allowable combinations of thrust and wing loadings that
satisfy the two performance requirements considered here. The main consequence
of increased throttle ratio, as expected, is to reduce TsL/Wro by sustaining thrust
to higher values of M0 and 00 (see Fig. 2.Elb).
The selection of a thrust loading and wing loading from Fig. 2.E2 is a compro-
mise of many factors. For a given Wro, a low (Wro/S) value means large wing
area while a high value of (TsJ Wro) results in a large thrust requirement. In
addition, a low wing loading reduces the airplane riding qualities and range and
can increase the aircraft radar cross section. We would prefer, therefore, relatively
low thrust and high wing loadings. We might, based on the constraint diagram of
Fig. 2.E2, select 1.0 and 64 lbf/ft 2 for our AAF thrust and wing loadings and an
engine throttle ratio of 1.07. However, we must take into account all performance
requirements as well as the takeoff ground roll drag in constructing the fighter's
complete constraint diagram.
When this is done, we employ the AEDsys Constraint Analysis software to
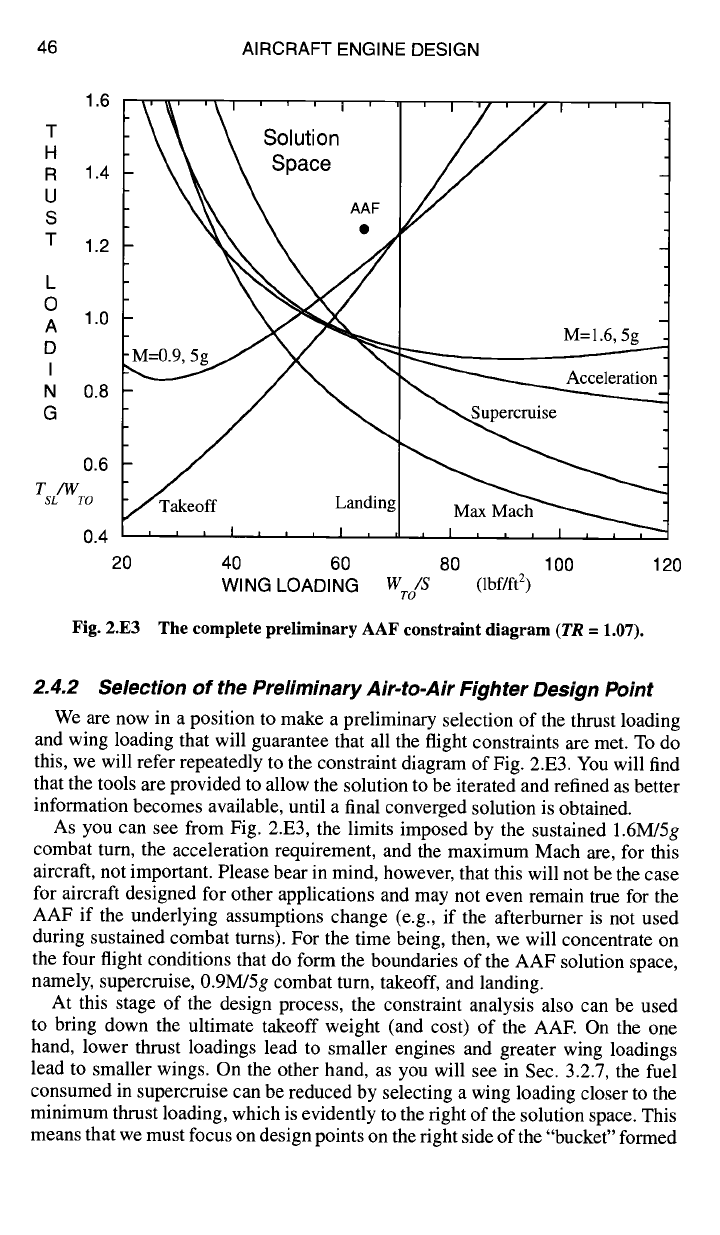
obtain and construct Fig. 2.E3, which is the complete constraint diagram we seek
in order to make a judicious selection of (TsL/Wro) and (Wro/S) for the AAE
Notice that the solution space in the diagram is bounded with constraints formed
by the supercruise, 0.9M/5g combat turn, takeoff, and landing RFP requirements.
It is interesting to superimpose the AAF solution space of Fig. 2.E3 on Fig. 2.3,
which contains the wing and thrust loadings of 22 fighter-type airplanes, as is done
in the composite Fig. 2.E4. We see that none of the contemporary fighters meets all
of the RFP requirements for the AAF, thus the need for a new airplane. However,
the larger YF-22 and YF-23 have similar thrust and wing loadings, which might
be expected because they have similar requirements.
46 AIRCRAFT ENGINE DESIGN
1.6
1.4
1.2
L
0
A 1.0
D
I
N 0.8
G
0.6
T/W
SL TO
0.4
20 40 60 80 100 120
WING LOADING W /S
(]bf/ft 2)
TO
Fig. 2.E3
The complete preliminary AAF constraint diagram
(TR =
1.07).
2. 4.2 Selection of the Preliminary Air-to-Air Fighter Design Point
We are now in a position to make a preliminary selection of the thrust loading
and wing loading that will guarantee that all the flight constraints are met. To do
this, we will refer repeatedly to the constraint diagram of Fig. 2.E3. You will find
that the tools are provided to allow the solution to be iterated and refined as better
information becomes available, until a final converged solution is obtained.
As you can see from Fig. 2.E3, the limits imposed by the sustained 1.6M/5g
combat tum, the acceleration requirement, and the maximum Mach are, for this
aircraft, not important. Please bear in mind, however, that this will not be the case
for aircraft designed for other applications and may not even remain true for the
AAF if the underlying assumptions change (e.g., if the afterburner is not used
during sustained combat turns). For the time being, then, we will concentrate on
the four flight conditions that do form the boundaries of the AAF solution space,
namely, supercruise, 0.9M/5g combat turn, takeoff, and landing.
At this stage of the design process, the constraint analysis also can be used
to bring down the ultimate takeoff weight (and cost) of the AAE On the one
hand, lower thrust loadings lead to smaller engines and greater wing loadings
lead to smaller wings. On the other hand, as you will see in Sec. 3.2.7, the fuel
consumed in supercruise can be reduced by selecting a wing loading closer to the
minimum thrust loading, which is evidently to the right of the solution space. This
means that we must focus on design points on the right side of the "bucket" formed

CONSTRAINT ANALYSIS 47
1.6
T
H
R 1.4
U
S
T
1.2
L
O
A 1.0
D
I
N
0.8
G
°° I
Ll%o
0.4
-
20
YF-23 • AAF
Mirage
4000 q
0.9M/5g Turn
Takeoff
F- 106A
.-
YF-22
MIG-31
AV-8B • SU-27
Harrier
• MIG-29
F- 16 X-29
JA37 •
Viggen F-20
F-4E •
KFir-C2 [ T-38 MIG-25
• •
F-16XL• F-5E Mirag
T-45
F-117A ~ A-10
40 60 80 100
WING LOADING
Wo/S
(lbf/ft 2)
120
Fig. 2.E4 Composite thrust loading vs wing loading--fighter aircraft and prelimi-
nary
AAE
near the juncture of the three constraining lines, preferably those near to the region
of previous thrust loading experience, which extends to about
TSL/WTO = 1.2
according to Fig. 2.E4. Fortunately, the wing loadings in the region are well within
the design experience or the industry, as seen in Fig. 2.E4, and high enough to assure
good handling qualities) It is equally important to avoid trying to put too fine a
point on our choice, lest the movement of any of the constraining lines caused
by improved estimates of aircraft and/or engine performance render it useless.
Following this logic, it appears that the preliminary design point
TSL/WTO
=
1.25
Wro/S
= 64 lbf/ft 2
TR
= 1.07
as indicated on Figs. 2.E3 and 2.E4, is a reasonable first choice, and this shall be
used as our decision. A host of interesting observations evolve, the most important
of which are the following:
1) The "new" capabilities of the AAF, namely short takeoff and landing, and
nonafterburning supercruise have "driven" the design.
2) Relieving the takeoff constraint (by increasing
sTO
or
CL
max), the landing
constraint (by increasing
SL
or providing reverse thrust), the 0.9M combat turn (by
48 AIRCRAFT ENGINE DESIGN
decreasing the number of gs), and the supercruise constraint (by decreasing the
supercruise Mach number) simultaneously would do little to reduce the required
TsL/Wro because of the bunching of the other constraints in the same neighbor-
hood. The good side of this situation is that the resulting engine will be running
near its full thrust at many flight conditions, so that its size will not be made ex-
cessively large by any single requirement, and its performance is liable to remain
high over the entire mission. This often happens when the RFP is the result of
thoughtful consideration and balancing of the requirements.
3) The drag chute is a bargain. Without it TslJ Wro would increase beyond any
reasonable limit because Wro/S = 50.8 lbf/ft 2 with no drag chute.
4) The throttle ratio has migrated in the direction of the supercruise 00 = 1.15
(see Appendix D).
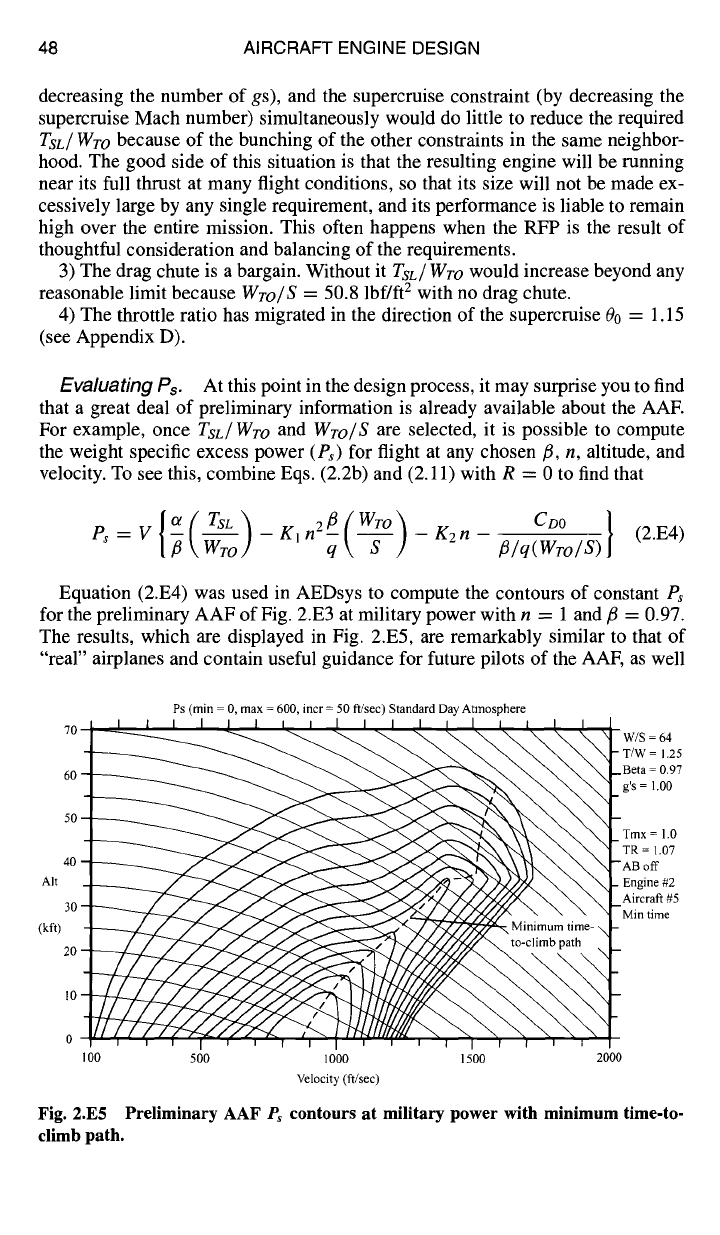
Evaluating Ps. At this point in the design process, it may surprise you to find
that a great deal of preliminary information is already available about the AAE
For example, once Tsl./Wro and Wro/S are selected, it is possible to compute
the weight specific excess power (Ps) for flight at any chosen/3, n, altitude, and
velocity. To see this, combine Eqs. (2.2b) and (2.1 l) with R = 0 to find that
P~ = V \-~oroJ - K1 q \---~-j - Kz n ~/q(WTo/S) (2.E4)
Equation (2.E4) was used in AEDsys to compute the contours of constant Ps
for the preliminary AAF of Fig. 2.E3 at military power with n = 1 and/~ = 0.97.
The results, which are displayed in Fig. 2.E5, are remarkably similar to that of
"real" airplanes and contain useful guidance for future pilots of the AAF, as well
Ps (min 0, max - 600, incr - 50 fl/sec) Standard Day Atmosphere
70 I I I [ ] ] I I [ ] ] ] | [ I I ] ] W/S = 64
60 _Beta = 0.97
g's = 1.00
,o
- TR = 1.07
40 -AB off
AIt Engine #2
30 .Aircrat~ #5
Min time
(kit)
20
10
100 500 1000 1500 2000
Velocity (ft/sec)
Fig. 2.E5 Preliminary AAF
Ps
contours at military power with minimum time-to-
climb path.

CONSTRAINT ANALYSIS 49
as for analyses. Fighter pilots routinely compare these Ps diagrams for their aircraft
with those of their potential adversaries in order to determine where in the flight
envelope they enjoy the greatest combat advantage.
Further, Fig. 2.E5 provides a graphic method for determining the minimum
time-to-climb flight path from a lower to a higher energy height. Equation (2.2b)
rewritten as
f2 fz~ -e2 dZe
At ---- dt =
,
es
(2.E5)
shows that the minimum time-to-climb from
Zel(hl,
V1) to the higher energy level
Ze2(h2,
V2) corresponds to the flight path that produces the maximum specific
excess power
Ps
at each
Ze.
This maximum occurs at the point of tangency between
a line of constant energy height and the contour line of the maximum Ps attainable
for that energy height. For
Ze
= 70 kft, for example, this tangency occurs at Ps =
320 ft/s, V = 1480 ft/s, and h = 36 kft. Continuing in this vein, one can find the
minimum time-to-climb flight path, from
Ze
of 13 kft at sea level to a
Ze
of 96 kft
at an altitude of 57 kft, as shown in Fig. 2.E5.
These preliminary quantitative results will, of course, change once the final
selection of the AAF design point has been made and as improved models of the
aircraft and engine performance are developed and used.
There are several other features of the
Ps
contours of Fig. 2.E5 that are striking
and noteworthy, and they can be usefully generalized to applications beyond the
AAE First, the theta break line of 1.07 at the peak of each contour is clearly
visible, and the value of moving it nearer to the supercruise flight condition is
evident. Second, the dip of each contour caused by the transonic drag rise near
M = 1 is also clearly visible. Third, the discontinuity on the right-hand side of each
contour marks the atmospheric tropopause. Finally, the minimum time-to-climb
path is quite similar to the theta break line because of the dominant influence of
engine thrust on G, but not identical because aircraft drag also contributes to the
calculation [see Eq. (2.E4)].
2.4.3 Complete AAF Constraint Boundary Computations
The constraint computational procedure and results for the performance require-
ments in Table 2.E1 follow. The same procedure is used in each constraint bound-
ary calculation. First, the applicable constraint boundary equation from Sec. 2.2
is written. Next, data to determine the values of all constants as they appear from
left to right in the equation are listed. This is followed by the specific constraint
boundary equation resulting from the given data. Finally, some solution sets of
this equation are tabulated. These are the data plotted in Figs. 2.E3 and 2.E4. The
same calculations can be performed and the boundaries plotted much more rapidly
using the Constraint Analysis portion of the AEDsys software included with this
textbook. An additional benefit of the software is that it constitutes a checklist of
the quantities required for the calculation of any chosen constraint boundary. The
individual values were obtained as described in Sec. 2.4.1, but it must be empha-
sized that they can be altered for the purpose of exploration at the discretion of the
reader.
