Mattingly J.D., Heiser W.H., Pratt D.T. Aircraft Engine Design

Подождите немного. Документ загружается.

20 AIRCRAFT ENGINE DESIGN

R 1.6

S 1.4

Landing

A 1.2

N 1.0

0.8

TsL/Wro

0.6

20 40 60 80 100 120

WING LOADING

W /S

(lbf/ft 2)

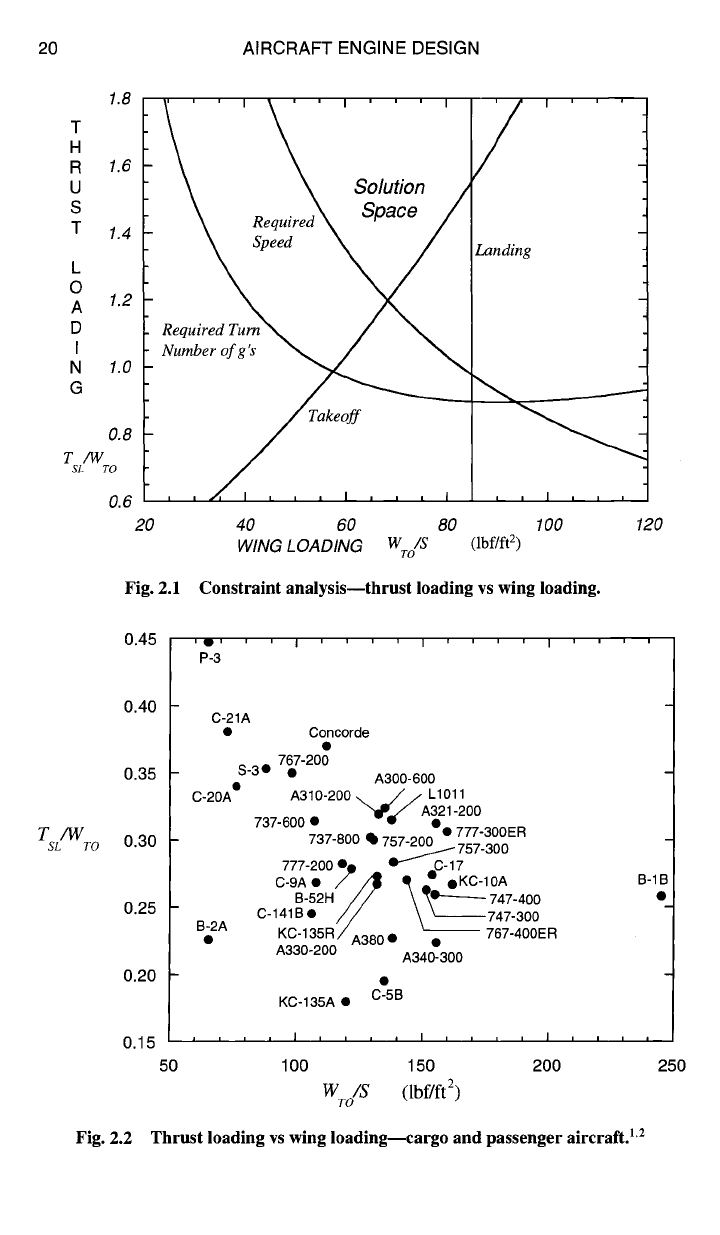
Fig. 2.1 Constraint analysis--thrust loading vs wing loading.

0.45

0.40

0.35

TSL'/WTo

0.30

0.25

0.20

P-3

C-21A

• Concorde

S-30 767-200

A300-600

C-20A A310-200 ... _.~/ L1011

~../ A321-200

737-600 • m O• 777-300ER

737-800 ~

7~757.300

777-200 •a eC- 17

c-gA. /-AI ~Z .Kc-loA

B-52H // \ "~w---------- 747-400

C-141B• // \ \ 747-300

B-2A KC-135R / A380 • -- • 767-400ER

A330-200 A340-300

KC-135A • C-5B

0,15

, , , , I , , , , I , , , , I , , , ,

50 100 150 200

WFo/S (lbf/ft 2)

Fig. 2.2 Thrust loading vs wing loading--cargo and passenger aircraft.

B-1E

250

CONSTRAINT ANALYSIS 21

T /W

SL TO

1.40

1.20

1.00

0.80

0.60 -

0.40

i i

,i,,,i

' i

YF-23 •

YF-22 SU-27

• AV-8B •

MIG-31 Harrier

Mirage •

4000 • F-150 • MIG-29

F-16

• X-29

Mirage • F-20 F-111F

2000 • JA37

Viggen F-4E

F-14B/D ~

KFir-C2 • •

• MIG-25 •

F-106A • F 15E

T-38 • • • F/ 18E/F

F-16XL • Mirage F1

T-45 • F/A-18NB

•

A-10

F-117A •

T-37

0.20 '

I I I ~ J I ~ ~ ~ I i ~

20 40 60 80 100 120 140

W /S

(lbflft 2)

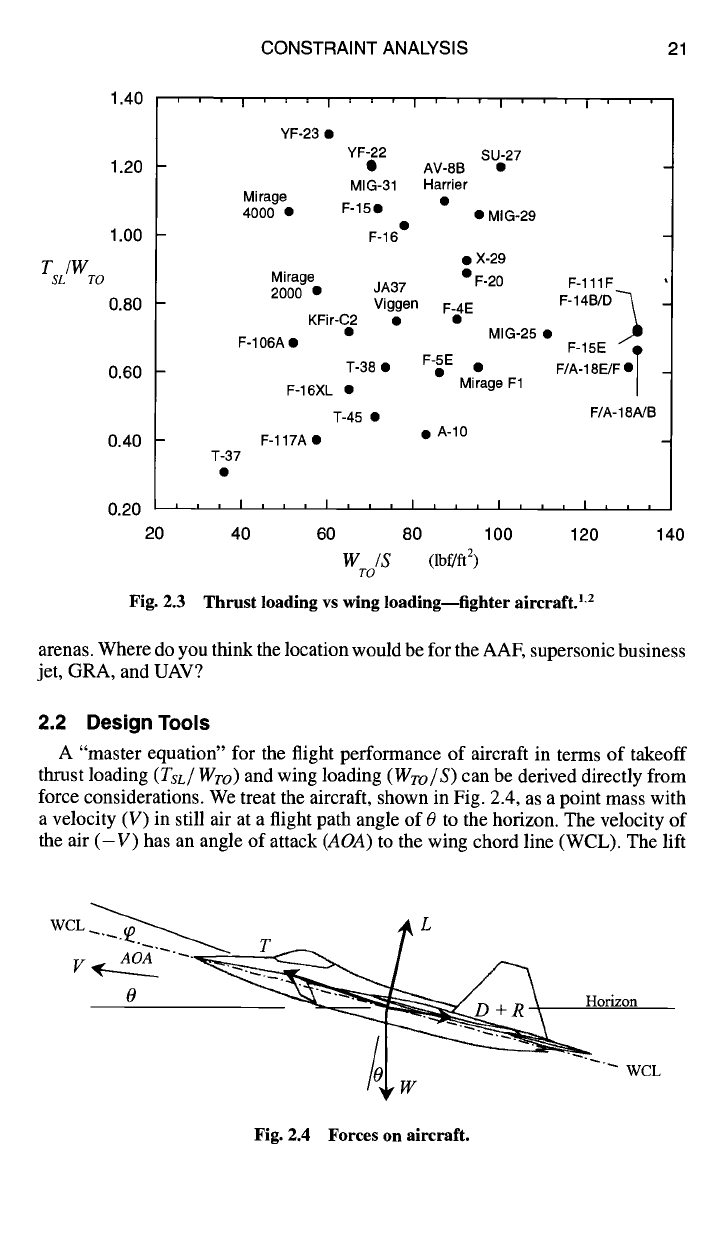
Fig. 2.3 Thrust loading vs wing loading--fighter aircraft. 1-2

arenas. Where do you think the location would be for the AAF, supersonic business

jet, GRA, and UAV?

2.2 Design Tools

A "master equation" for the flight performance of aircraft in terms of takeoff

thrust loading

(TsL/Wro)

and wing loading

(Wro/S)

can be derived directly from

force considerations. We treat the aircraft, shown in Fig. 2.4, as a point mass with

a velocity (V) in still air at a flight path angle of 0 to the horizon. The velocity of

the air (-V) has an angle of attack

(AOA)

to the wing chord line (WCL). The lift

WCL ~ ~ L

OS w

~~ WCL

Fig. 2.4 Forces on

aircraft.

22 AIRCRAFT ENGINE DESIGN

(L) and drag (D + R) forces are normal and parallel to this velocity, respectively.

The thrust (T) is at an angle 9 to the wing chord line (usually small). Applying

Newton's second law to this aircraft we have the following for the accelerations:

Parallel to V:

W WdV

T cos(AOA + ~o) - W

sin0 - (D + R) = --all -- (2.1a)

go go dt

Perpendicular to V:

L + T sin(AOA + 9) -

Wcos0 = --a± (2.1b)

Multiplying Eq. (2.1a) by the velocity (V), we have the following equation in the

direction of flight:

{T cos(AOA + ~o) - (D + R)}V = W V

sin0 +

(i)

Note that for most flight conditions the thrust is very nearly aligned with the

direction of flight, so that the angle

(AOA + ~o)

is small and thus

cos(AOA + ~) .~ 1.

This term will therefore be dropped from the ensuing development, but it could be

restored if necessary or desirable. Also, multiplying by velocity has transformed

a force relationship into a power, or time rate of change of energy, equation. This

will have profound consequences in what follows. Since V sin 0 is simply the

time rate of change of altitude (h) or

V sin 0 = -- (ii)

then combining equations (i) and (ii) and dividing by W gives

T-(D+R)v=

d{h V 2}

dze

w =-g

(2.2a)

where

Ze = h + V2/2go

represents the sum of instantaneous potential and kinetic

energies of the aircraft and is frequently referred to as the "energy height." The

energy height may be most easily visualized as the altitude the aircraft would

attain if its kinetic energy were completely converted into potential energy. Lines

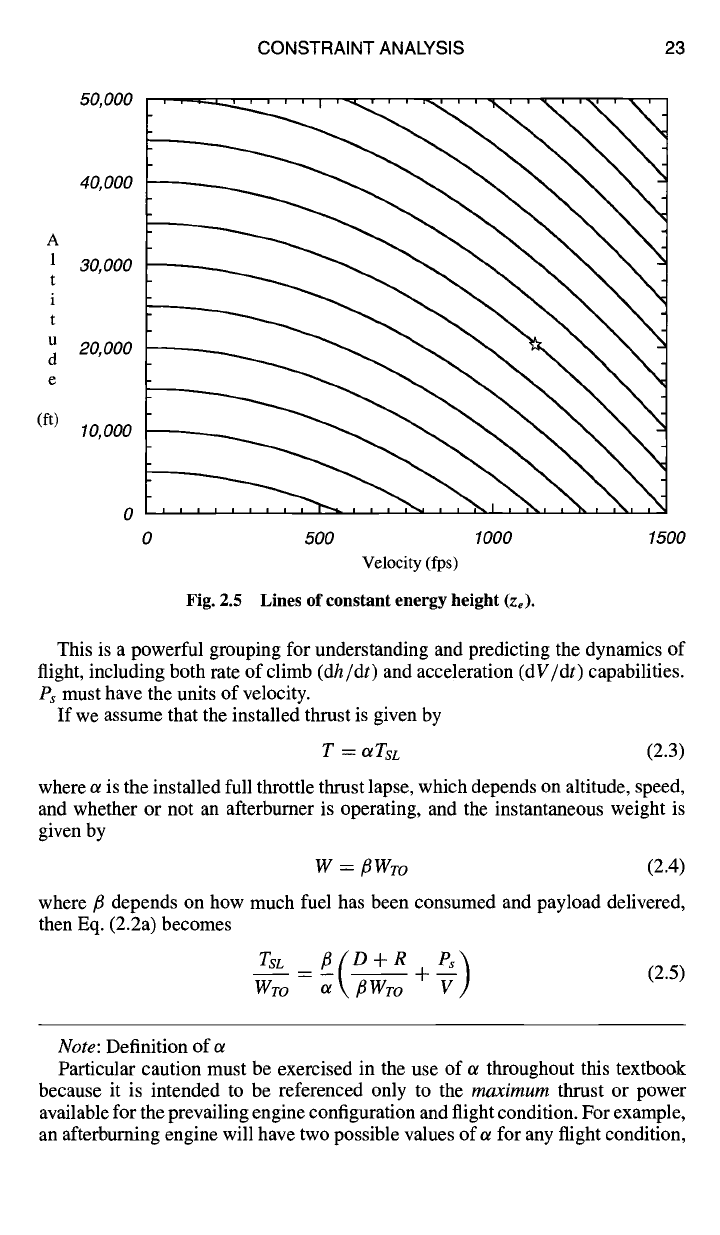
of constant energy height are plotted in Fig. 2.5 vs the altitude-velocity axes. The

flight condition (h = 20 kft and V = 1134 fps) marked with a star in Fig. 2.5

corresponds to an energy height of 40 kft. Excess power is required to increase the

energy height of the aircraft, and the rate of change is proportional to the amount

of excess power.

The left-hand side of Eq. (2.2a) in modern times has become recognized as a

dominant property of the aircraft and is called the weight specific excess power

dze __ d h +

(2.2b)

Ps- dt dt

CONSTRAINT ANALYSIS 23

(ft)

50,000

40,000

30,000

20,000

10,000

i i I i ~ i I i i i i i i i i i i i i i i

0 500 1000 1500

Velocity (fps)

Fig. 2.5 Lines of constant energy height (ze).

This is a powerful grouping for understanding and predicting the dynamics of

flight, including both rate of climb

(dh/dt)

and acceleration

(dV/dt)

capabilities.

Ps must have the units of velocity.

If we assume that the installed thrust is given by

T = etTsL

(2.3)

where ot is the installed full throttle thrust lapse, which depends on altitude, speed,

and whether or not an afterburner is operating, and the instantaneous weight is

given by

W = fl WTO

(2.4)

where fl depends on how much fuel has been consumed and payload delivered,

then Eq. (2.2a) becomes

Wro - ~ \ Tff-~ro +

(2.5)

Note:

Definition of ot

Particular caution must be exercised in the use of a throughout this textbook

because it is intended to be referenced only to the

maximum

thrust or power

available for the prevailing engine configuration and flight condition. For example,

an afterbuming engine will have two possible values of ot for any flight condition,

24 AIRCRAFT ENGINE DESIGN

one for mil power and one for max power (see Sec. 1.11E of RFP). You must

differentiate carefully between them. Lower values of thrust are always available

by simply throttling the fuel flow, thrust, or power.

It is equally important to remember that both T and

TSL

refer to the "installed"

engine thrust, which is generally less than the "uninstalled" engine thrust that

would be produced if the external flow were ideal and created no drag. The dif-

ference between them is the additional drag generated on the external surfaces,

which is strongly influenced by the presence of the engine and is not included in

the aircraft drag model. The additional drag is usually confined to the inlet and

exhaust nozzle surfaces, but in unfavorable circumstances can be found anywhere,

including adjacent fuselage, wing, and tail surfaces. The subject of "installed" vs

"uninstalled" thrust is dealt with in detail in Chapter 6 and Appendix E.

Now, using the traditional aircraft lift and drag relationships,

L = nW = qCLS

(2.6)

where n = load factor = number of g's (g = go) _L to

V(n

= 1 for straight and

level flight even when

dV/dt ~

0),

= qCDS

(2.7a)

and

R = qCDRS

(2.7b)

where D and CD refer to the "clean" or basic aircraft and R and CDk refer to

the additional drag caused, for example, by external stores, braking parachutes or

flaps, or temporary external hardware. Then

CL-- qS -- q

Further, assuming the lift-drag polar relationship,

CD = KIC2L + K2CL + CDO

(2.9)

Equations (2.7-2.9) can be combined to yield

D+R=qS{KI(qfl~°)2+K2(n~flq V~°)+CDo+CDR}

(2.10)

Finally, Eq. (2.10) may be substituted into Eq. (2.5) to produce the general form

of the "master equation"

o) ]

WTO t~ [ flWro L \ q + K2

CDO "~- CDR "J- ~-

(2.11)

It should be clear that Eq. (2.11) will provide the desired relationships between

TSL/WTO

and

Wro/S

that become constraint diagram boundaries. It should also

be evident that the general form of Eq. (2.11) is such that there is one value of

CONSTRAINT ANALYSIS 25

WTo/S for which

TSL / WTO

is minimized, as seen in Fig. 2.1. This important fact

will be elaborated upon in the example cases that follow.

Note: Lift-drag polar equation

The conventional form of the lift-drag polar equation is 3

CD ~-

Cnmin +

K'C 2 +

K'(CL -

CLmin) 2

where K' is the inviscid drag due to lift (induced drag) and K" is the viscous drag

due to lift (skin friction and pressure drag). Expanding and collecting like terms

shows that the lift-drag polar equation may also be written

/¢" t I t"~ 2

CD ~-"

(K' + K")C2L

- (2K't CLmin)CL q- (CDmin ~ .~ ~Lmin]

where

CD = K1C 2 + K2CL + CDO

(2.9)

K1 = K' + K"

K2 = -2K"CLmin

l¢,'tl t~2

CDO

min -'[- *~ ~L min

Note that the physical interpretation of CDO is the drag coefficient at zero lift. Also,

for most high-performance aircraft CL min

0, SO that K2 ,~ 0.

A large number and variety of special cases of Eq. (2.11) will be developed in

order both to illustrate its behavior and to provide more specific design tools for

constraint analysis. In all of the example cases that follow, it is assumed that the ot

of Eq. (2.3), the fl of Eq. (2.4), and the K1, K2, and CDO of Eq. (2.9) are known. If

they change significantly over the period of flight being analyzed, either piecewise

solution or use of representative working averages should be considered.

2.2.1 Case 1: Constant Altitude~Speed Cruise

(Ps = O)

Given: dh/dt = O, dV/dt = 0, n = 1 (L = W), and values of h and V (i.e., q).

Under these conditions Eq. (2.11) becomes

TsL _ fl Ka + K2 + (2.12)

Wro ot q \--S-] fl/q(Wro/S)

This relationship is quite complex because TsL/Wro grows indefinitely large

as WTo/S becomes very large or very small. The location of the minimum for

TsJ Wvo can be found by differentiating Eq. (2.12) with respect to WTo/S and

setting the result equal to zero. This leads to

S -Iminr/W

o~. &~

, , ~" ~

-e ~11

-~1 ~ ~- + ~

~ +

~ V

"* ~l'~

~ +

|| Jr-

e~. =~ r~"

~,-~ ..

a.~ ~.-~ g.~ ~ ~~

-=: .~ + n

~~ +

~ ~ ~ ~"

~ o ~

~1 ~

~ b~

o%1o

~.~.

i !

IiI- ~

-4-

-I1

--I

ITI

G')

or)

CONSTRAINT ANALYSIS 27

L=nWI,.--AW

,~ ~ ~ bank angle

: (._W_W ~V 2 ~ : cos-'(1/n)

" Y W

Fig. 2.6 Forces on aircraft in turn.

and

TSL

1 nfl

{2~/(CD0 +

CDR)KI +

K2}

V;S o Jmi. =

Occasionally n is stipulated in terms of other quantities. In the case of a level,

constant velocity turn, for example, where the vertical component of lift balances

the weight and the horizontal component is the centripetal force, n is as shown in

Fig. 2.6.

It follows from the Pythagorean Theorem that

\go /

n= l + \ goRc ]

and

(2.16)

(2.17)

which can be used when the rotation rate (~2) or the radius of curvature

(Re)

given rather than the load factor (n).

2.2.4 Case 4: Horizontal Acceleration [Ps = (V/go)

V/dt)]

Given:

dh/dt

= 0, n = 1 (L = W) and values of

Vinitial, Vfinal,

and

Atallowable.

Under these conditions Eq. (2.11) becomes

TSL B [ 13 {WTo ~ CDO'q-CDR 1 dV I

-- r'K1

Wro - -dl q ~----~-} + K2 +13/q(Wro/S) + ~--d-t- I

(2.18a)

which can be rearranged to yield

{ 13(WTo~ CDo+CDR I

1 dV _ ot TSL K1 + K2 +

(2.18b)

go dt 15 WTO q \ S-,] fl~q-('WT-~) I

Strictly speaking, Eq. (2.18b) must be integrated from

Vi,itiat

V~nal

in order to

find combinations of thrust loading and wing loading that satisfy the acceleration

28 AIRCRAFT ENGINE DESIGN

time criterion. A useful approximation, however, is to select some point between

Vi, iti~t

and

Villa1

at which the quantities in Eq. (2.18a) approximate their working

average over that range, and set

ldV

l ( Vfinal = Vinitial )

go dt go

Atallowable

In this case the constraint curve is obtained from Eq. (2.18a), which again has the

properties of Eq. (2.12) including the location of the minimum

Tsr/Wro.

Equation (2.18b) can be numerically integrated by first recasting the equation

1 [v~.,., VdV

fv~2,aldV 2

Atallowable = --

-- --

(2.19a)

go a v~,i,i~ Ps

2g0

Jvi],~ Ps

where

TsL K1 + K2 +

(2.19b)

Ps = V -~ Wro q \---S-] fl/q(WTo/S)A

The solution of the required thrust loading

(TsL/Wro)

for each wing loading

(WTo/S)

can be obtained by the following procedure:

1) Divide the change in kinetic energy into even sized increments, and calculate

the minimum thrust loading [maximum

TSL/WTO

corresponding to Ps = 0 in

Eq. (2.19b) for all kinetic energy states].

2) Select a thrust loading larger than the minimum and calculate the acceleration

time (A t) using Eqs. (2.19a) and (2.19b). Compare resulting acceleration time with

Atallowable.

Change the thrust loading and recalculate the acceleration time until it

matches

Atallowabl e.

2.2.5 Case 5: Takeoff Ground Roll

($G),

when

TSL

(D + R)

Given:

dh/dt

= 0 and values

Of SG, p,

CLrnax, and

VTO = kToVsTAL L.

Under these conditions Eq. (2.5) reduces to

TsL

WTO

which can be rearranged to yield

fl dV fl dV

ago dt ago ds/V

fl (Wro~v

ago \ T-s-sS / d V

and integrated from s = 0 and V = 0 to takeoff, where s = so and V =

Vro,

with the result that

(WTo

S G ----

a / 2g0

provided that representative takeoff values of a and fl are used. Defining

Vro = kro VSrALL

(2.20)

CONSTRAINT ANALYSIS 29

where kro is a constant greater than one (generally specified by appropriate flying

regulations) and VSrAU~ is the minimum speed at which the airplane flies at CL m,x,

then

qCLmaxS

= 1 2

~PV~TALLCLmaxS

flWTo

V ,ALL (W O)

% -

2 2 P--~L ~ \--ff-]

(2.21)

where

Under these conditions

D+R

Wro

so that Eq. (2.5) becomes

rsL

WTO

(CD -~- CDR -- I~roCL)qS -t- tXTo~WTo

t ~ WTO

{ fl('~OTO) ldV}

fl ~ro q S +/Xro+--

ot go

~ro = CD + CoR -/zroCL (2.24)

which can be rearranged and integrated, as in Case 5, to yield

{ /I(~ "~CLmaxl}

(2.25)

_ fi(Wro/S) In 1 - ~ro TSL IZro]

Pgo~ro WTO

provided that representative takeoff values of ot and fl are used.

For this case TSL/Wro must increase continuously with Wro/S, but in a more

complex manner than in Case 5. That result is again obtained in the limit as all

terms in ~ro approach zero and In (1 - e) approaches -e, whence

~( Wro / S) ~ro

s G

PgO~TO (Ol/~)(ZsL/WTo)fLmax/k20

WTO ~ SGPgoCLmax

(2.22)

(2.23)

2.2.6 Case 6: Takeoff Ground Roll

($G)

Given: dh/dt = 0 and values of p, D = qCDS, CLmax, VTO

= kToVsTALL,

and

R = qCDRS + #ro(fiWro - qCLS).

with the final result that

WTO 0l SGPgoCLmax

For this limiting case TSL/WTO is directly proportional to Wro/S and inversely

proportional to s~.