Mattingly J.D., Heiser W.H., Pratt D.T. Aircraft Engine Design

Подождите немного. Документ загружается.

30 AIRCRAFT ENGINE DESIGN

V=0

Rotation

V~o

Ground Roll

S G ..I

~1 SR

Transition

gel

~ hTR

~1- Sre ~ SoL

STO

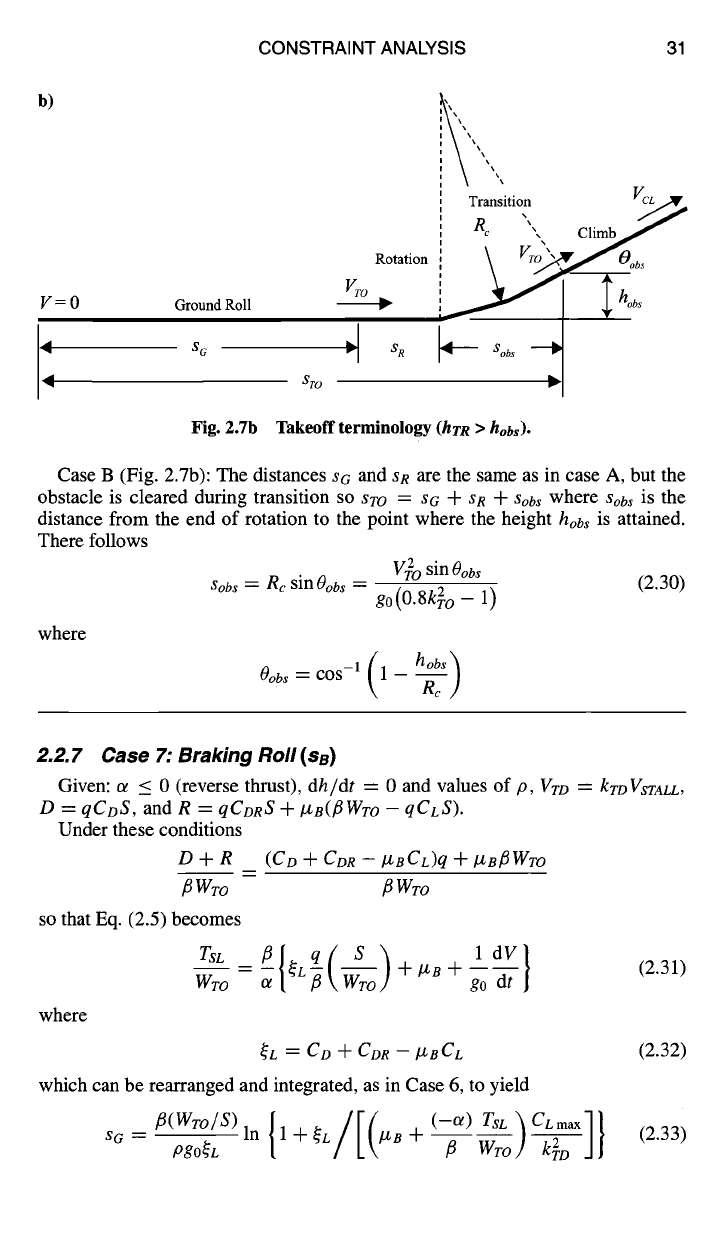
Fig. 2.7a Takeoff terminology (hrR <

hobs).

hobs

Note:

Total takeoff distance

Two cases arise:

Case A (Fig. 2.7a): The total takeoff distance

(sro)

can be analyzed as ground

roll

(SG)

plus three other distances: the first

(SR)

to rotate the aircraft to the takeoff

lift condition (traditionally CL

= 0.8CLmax)

while still on the ground; the second

(SrR)

to transit to the angle of climb direction; and the last

(scD

to clear an obstacle

of given height. These distances may be estimated as followsl:

SR = tR Vro = tRkro~/{2fl /(pCL

max)}(WTo/ S )

(2.26)

where

is a total aircraft rotation time based on experience (normally 3 s),

STR

sin

OCL -- Vr2°

sin

OCL

go(n-

VT20 sin

OCL k2ro

sin

OCL 2fl ( Wro

SrR = go(O.8k2o _

1) = g0~.8~ro --- 1) ~ \-S-,] (2.27)

where

Occ

is the angle of climb, which can in turn be obtained from Eq. (2.2a) as

dh T-D

sin

Ocz - --

V dt W

and, if

hobs > hrR

hobs -- hTR

SCL --

(2.28)

tan

OcL

where

hobs

is the required clearance height and

hrR

is given by the following

expression, provided that

hobs > hrR:

VZo(1--cosOcL) kZo(1--cOSOcL) 2fl (t~o)

hrR= go(O.8k2o -

1) ---- g0(0---~8"-k2~o--1)

PCLmax --

(2.29)

CONSTRAINT ANALYSIS

Rotation

V~o

V = 0 Ground Roll

SG • S R

STO

Transition

V " Clim/

~- Sob ~ ~

Fig. 2.7b

Takeoff terminology

(hTR > hobs).

Case B (Fig. 2.7b): The distances SG and sn are the same as in case A, but the

obstacle is cleared during transition so

STO = Sa + SR + Sobs

where

Sobs

is the

distance from the end of rotation to the point where the height

hobs

is attained.

There follows

V2o

sin

Oobs

Sobs = Rc sinOobs go(O.8k2o -

1) (2.30)

where

hobs

Oobs = COS

-1 1--

Rc I

2.2.7 Case 7: Braking ROII(SB)

Given: ot < 0 (reverse thrust),

dh/dt

= 0 and values of p, VrD =

krDVsTAIZ,

D = qCDS,

and R =

qCDRS + Izs(flWro -- qCLS).

Under these conditions

D + R (Co -~- CDR -- lZBCL)q if" tZBflWTo

t~ WTO t ~ Wro

so that Eq. (2.5) becomes

TsL

- ~ ~-~ ~oro ~ --gi-

(2.31)

WTO go

where

~L = CD -'[- CDR -- ].I"BCL

(2.32)

which can be rearranged and integrated, as in Case 6, to yield

_fl(WTo/S) ln{I+~L/[(IZB + (--Or)TsL~CLmax]I

sa Pgo~r

7- Wro]

k2--~-D ]

] (2.33)

32 AIRCRAFT ENGINE DESIGN

provided that representative landing values of a and fi are used and where kTD is a

constant greater than one (generally specified by appropriate flying regulations).

For this case reverse thrust can be used to great advantage. If the second term in

the bracket of Eq. (2.33) is made much less than one by making (-a) very large,

then

S B --~

¢~(Wro/S) ~L

PgO~L

[(--~)It~](TsLIWTo)(CLmax/k2D)

WTO

(--Ol) SBPgoCLmax

(2.34)

Note: Total landing distance

The total landing distance (sL) can be analyzed as braking roll (sB) plus two

other distances (see Fig. 2.8): the first (SA) to clear an obstacle of given height and

the second (SFR) a free roll traversed before the brakes are fully applied. These

distances may be estimated as follows: 1

S A =

pgo(C~ + coR) -- \ k~ob, + k~D +

C L max

2h obs

(c. + co.)(ko~s + ~)

(2.35)

where hobs is the height of the obstacle and the velocity at the obstacle is

gobs =

kobs VSTALL

(2.36)

and

SFR = tFR

VTD : tFRkTD~// {

2 fl / (pC L

max) }( WTo / S)

(2.37)

gobs

-~-*~ ~Approach

h °b~

Free Roll

VrD k

Braking V = 0

sA J I.

Iv[ SFR I "~l S B

SL Yl

Fig. 2.8 Landing terminology.

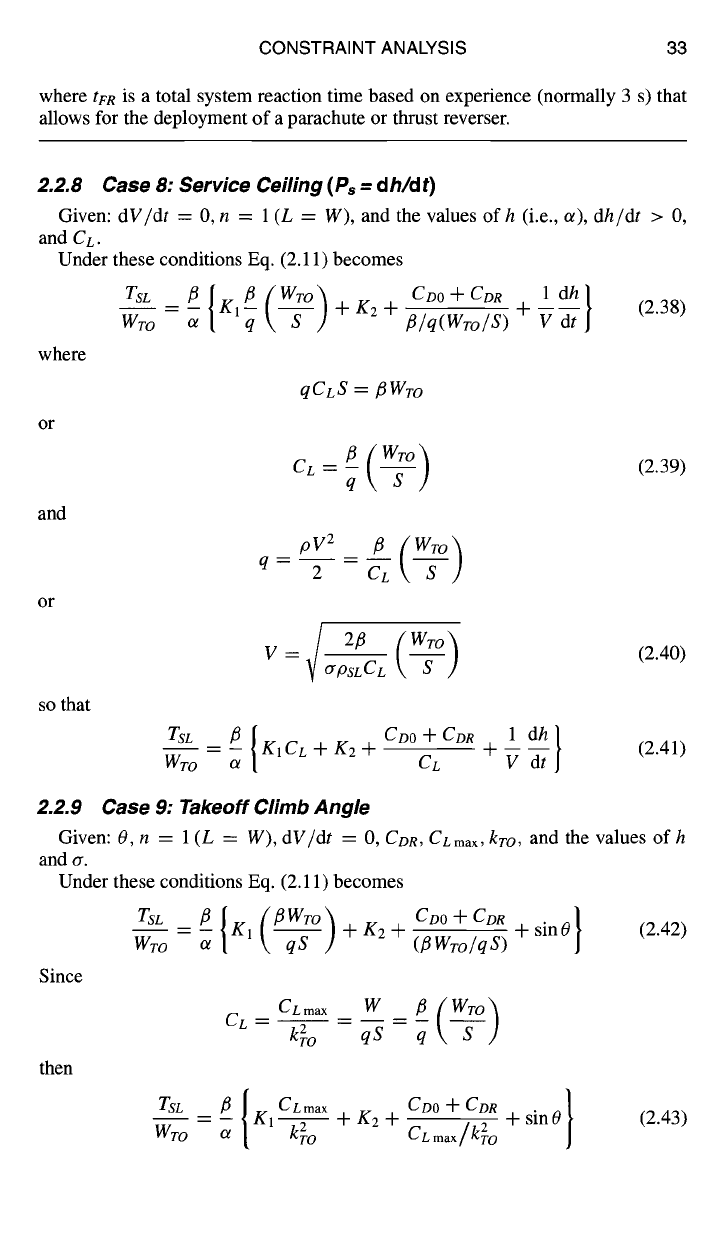
CONSTRAINT ANALYSIS 33

where

tFR

is a total system reaction time based on experience (normally 3 s) that

allows for the deployment of a parachute or thrust reverser.

2.2.8 Case 8: Service Ceiling (Ps = dh/dt)

Given:

dV/dt = O, n = 1 (L = W),

and the values of h (i.e., or),

dh/dt > O,

and

CL.

Under these conditions Eq. (2.11) becomes

TSL -- fl

-- + K2 + fl/q(WTo/S)

Wro ot

where

and

so that

qCL S = flWTo

,dh}

+ V ~- (2.38)

CL = fl-- (~ 0

(2.39)

q-- 2 --(L

(2.40)

Since

then

and cr.

Under these conditions Eq. (2.11) becomes

TSL fl K1

+K2+

W~o ,~ \ ~ )

C L max W

CL -- k2 ° -- qS --

TSL

fl [ CLmax

+ +

CDO "~ CDR }

(flWro/qS) +

sin 0 (2.42)

CDO "~ CDR I

CLm~x/k2 ° +

sinO J (2.43)

2.2.9 Case 9: Takeoff Cfimb Angle

Given:

O, n = 1 (L = W), dV/dt

= 0,

CDR , CLmax,

kro,

and the values ofh

____{ CDO"~-CDR

l dh}

TSL fi K1CL + K2 + +

(2.41)

Wro ~ CL V d[

34 AIRCRAFT ENGINE DESIGN

and

V=VT°=~ O'PSL2t~k2OcL

max (~O) (2.44)

is employed to find Mro for a given Wro/S and thus the applicable values of

et, K1, K2, and Coo. Because they vary slowly with WTo/S, the constraint bound-

ary is a line of almost constant TSL/Wro.

2.2.10 Case 10: Carrier Takeoff

Given: n = 1 (L = W), Vro, dV/dt, CL

max,

kTo, 1~, and the values of h and a.

Solving Eq. (2.44) for wing loading gives

WTO PsL C L max V•O

T max = 2~k2ro (2.45)

where the takeoff velocity (Vro) is the sum of the catapult end speed (Ve.d) and

the wind-over-deck (Vwod) or

Vro = Ve,d + Vwoa (2.46)

A typical value of kro is 1.1 and of Ve,d is 120 kn (nautical miles per hour).

Wind-over-deck can be 20 to 40 kn, but design specifications may require launch

with zero wind-over-deck or even a negative value to ensure launch at anchor. This

constraint boundary is simply a vertical line on a plot of thrust loading vs wing

loading with the minimum thrust loading given, as already seen in Eq. (2.43), by

TSL fl K1- + K2 + + --

(2.47)

L ~ Jmin =

k2o CLmax/k2o go

--~

where or, K1, KE, and Coo are evaluated at static conditions. A typical value of

the required minimum horizontal acceleration at the end of the catapult (dV/dt) is

0.3 go.

2.2.11 Case 11: Carrier Landing

Given: n = 1 (L = W),

VTD,

max,

kTD,

fl, and the values of h and ~r.

Rewriting Eq. (2.45) for the touchdown condition gives

WTO PsL C L

max

V~'D

--g- max = 2flk2ro (2.48)

where the touchdown velocity (Vro) is the sum of the engagement speed (Ve.g,

the speed of the aircraft relative to the carrier) and the wind-over-deck (Vwod), or

Vro = Veng + Vwod

A typical value ofkro is 1.15 and of Ve.g is 140 kn (nautical miles per hour). As

in Case 10, this constraint boundary is simply a vertical line on a plot of thrust

CONSTRAINT ANALYSIS 35

loading vs wing loading. The minimum thrust loading is given by Eq. (2.49):

o O,min = /K'

CDO ÷ CDR I

+ K 2 + CLmax/k2 D +

sin 0 J

(2.49)

where -0 is the glide-slope angle.

2.2.12 Case 12: Carrier Approach (Wave-off)

Given:

O, n = 1 (L = W),

VTD,

dV/dt, el, fi,

CDR, CLmax,

kTD, and the values

of h and a.

Because carrier pilots do not flair and slow down for landing but fly right into

the carrier deck in order to make certain the tail hook catches the landing cable, the

approach speed is the same as the touchdown speed (VrD). Rewriting Eq. (2.48)

for the approach condition gives

[WTo] (rpsLCLmaxV2D

(2.50)

-U max =

As in Cases 10 and 11, this constraint boundary is simply a vertical line on a plot

of thrust loading vs wing loading.

Under these conditions Eq. (2.11) becomes

--~dV}

max

CDO ÷ fOR __

IrSL1WTO..Jmin

=~--0/

K1---~--TD +g2+

CLmax/k2D

+ sin 0 + go

(2.51)

where -0 is the glide-slope angle and or, K1, K2, and

CDO are

evaluated at static

conditions. Typical wave-off requirements are an acceleration of 1/8 go while on

a glide-slope of 4 deg.

2.3 Preliminary Estimates for Constraint Analysis

Preliminary estimates of the aerodynamic characteristics of the airframe and of

the installed engine thrust lapse are required before the constraint analysis can be

done. The following material is provided to help obtain these preliminary estimates.

2.3.1 Aerodynamics

The maximum coefficient of lift

(CL

max)

enters into the constraint analysis dur-

ing the takeoff and landing phases. Typical ranges for CL max divided by the cosine

of the sweep angle at the quarter chord

(Ac/4) are

presented in Table 2.1, which is

taken from Ref. 4. This table provides typical

max for cargo- and passenger-type

aircraft. For fighter-type aircraft a clean wing will have

max ~

1.0 --+ 1.2 and a

wing with a leading edge slat will have CLmax ~ 1.2 -+ 1.6. The takeoff maximum

lift coefficient is typically 80% of the landing value.

AIRCRAFT ENGINE DESIGN

Table 2.1

CLmax

for high lift devices 4

High lift device Typical flap angle, deg

max/COS(Ac/4)

Trailing edge Leading edge Takeoff Landing Takeoff Landing

Plain 20 60

1.4 ~ 1.6 1.7 ~

2.0

Single slot 20 40 1.5 ~ 1.7 1.8 ~ 2.2

Fowler 15 40 2.0 ~ 2.2 2.5 ~ 2.9

Double sltd. 20 50 1.7 ~ 2.0 2.3 ~ 2.7

Double sltd. Slat 20 50 2.3 ~ 2.6 2.8 ---> 3.2

Triple sltd. Slat 20 40 2.4 ~ 2.7 3.2 ~ 3.5

The lift-drag polar for most large cargo and passenger aircraft can be estimated

(Ref. 5) by using Fig. 2.9 and Eq. (2.9) with

0.001 _< K" < 0.03, 0.1 <

CLmin

< 0.3, K' --

hARe

where the wing aspect ratio

(AR)

is between 7 and 10 and the wing planform

efficiency factor (e) is between 0.75 and 0.85. Note that

: ld'll("2 K2 -2K"CL

min

K1 = K' + K", Coo

CDmin + -~ "-'Lmin' :

The lift-drag polar for high-performance fighter-type aircraft can be estimated

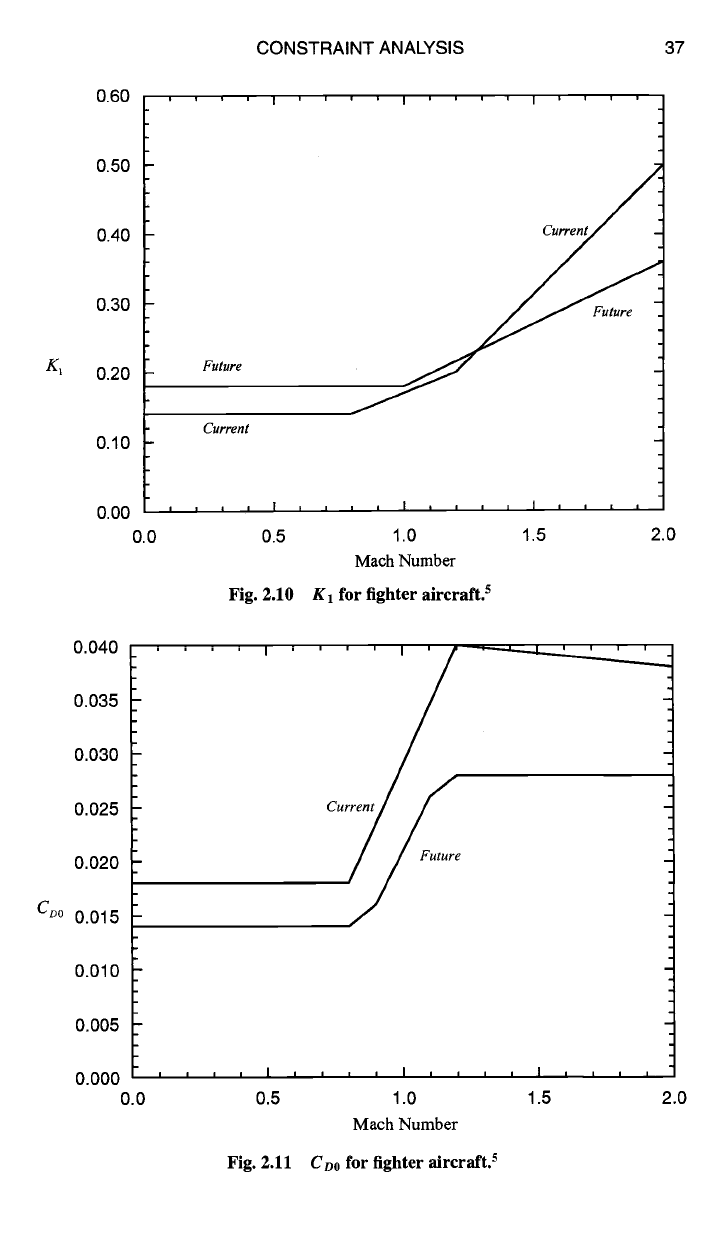
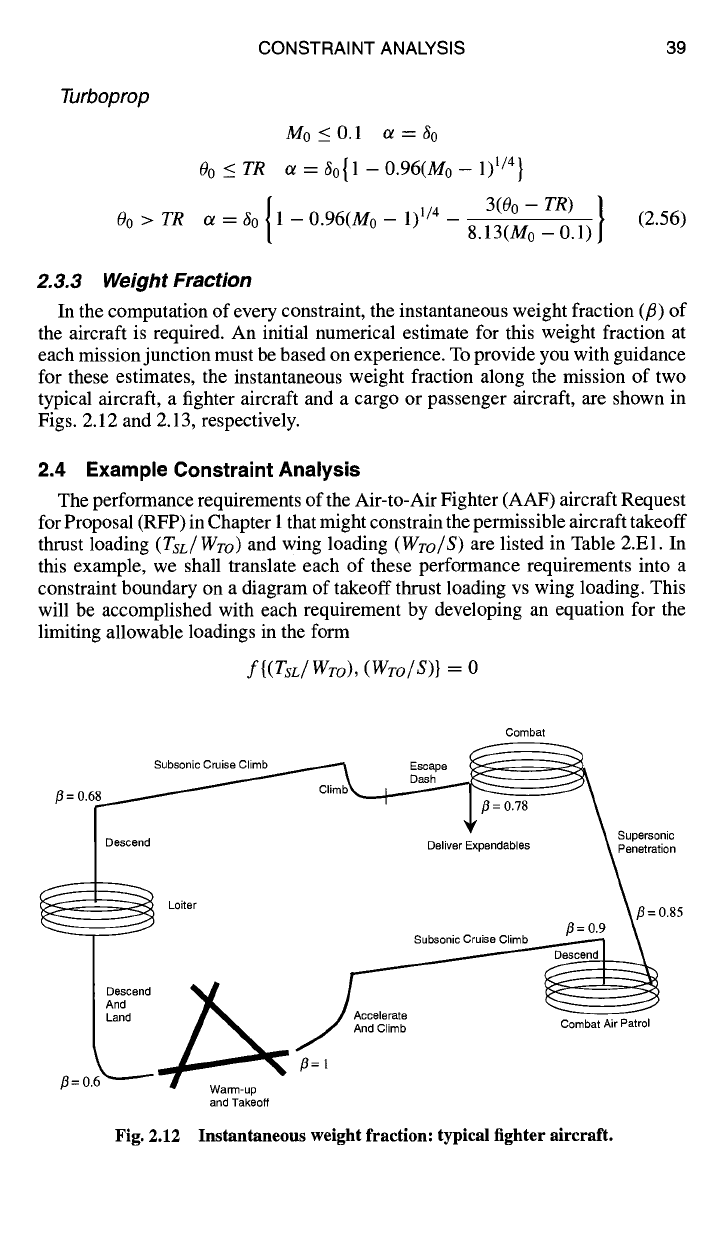
(Ref. 5) using Eq. (2.9), K: = 0, and Figs. 2.10 and 2.11.

Cmin

0.040

O. 035

0.030

0.025

0.020

0.015

0.010

0.005

0.000

0.0

' ' ' I ' ' ' I ' ' ' I ' ' '

Turboprop

Turbofan~jet

I I I

Fig. 2.9

I I i i I i i i I i i i I

0.2 0.4 0.6 0.8

Mach Number

CDmin

for cargo and passenger

aircraft, s

I I I

1.0

CONSTRAINT ANALYSIS 37

0.60

I '

' ' '

....

0.50

0.40

0.30

Kl 0.20

0.10

0.00

0.0

Future

Current

I I I I I l , l ~ , , , I i i t i

0.5 1.0 1.5

Mach Number

Fig. 2.10

K 1

for fighter aircraft, s

0.040

0.035

0.030

0.025

0.020

Cv° 0.015

0.010

0.005

I ' ' ' ' I '

Curr

, , , , I , , , , I , , , , I , , , ,

0.000

0.0 0.5 1.0 1.5

Mach Number

Fig. 2.11 CDo for fighter aircraft. 5

2.0

38 AIRCRAFT ENGINE DESIGN

2.3.2 Propulsion

The variation of installed engine thrust with Mach number, altitude, and after-

burner operation can be estimated by developing a simple algebraic equation that

has been fit to either existing data of company-published performance curves or

predicted data based on the output of performance cycle analysis (see Chapter 5)

with estimates made for installation losses. The following algebraic equations for

installed engine thrust lapse are based on the expected performance of advanced

engines in the 2000 era and beyond. These models use the nondimensional tem-

perature (8 and 80) and nondimensional pressure (8 and 80), defined next, and the

throttle ratio

(TR)

described in Appendix D. The rationale for these models has

a sound, fundamental basis that is developed in Mattingly 6 and confirmed by the

analysis of Appendix D.

8=T/T, td

and 8o=Tt/T~td=8(l+ff~-M~) (2.52a)

_Z_

6=P/P~ta

and 60=PJP~td=6 1+ (2.52b)

High bypass ratio turbofan ( Mo <

0.9)

8o < TR

ot = 6o{1 - 0.49v/~o}

8o > TR

ot=60{1-0.49v/-~o

Low bypass ratio, mixed flow turbofan

Maximum power:

8o > TR

Military power:

3(80 -rR ] (2.53

1.5 T Mo ]

8o < TR

ot=8o

ot = 6o{1 - 3.5(80 -

TR)/8o}

Oo < TR

a=0.66o

= 0.66o{1 - 3.8(80 -

TR)/Oo}

(2.54a)

8o > TR

(2.54b)

Turbojet

Maximum power:

8o < TR

t~ = 6o{1 - 0.3(80 - 1) - 0.1v~o }

{

l'5(8°--TR)} (2"55a)

8o >TR

ot=6o 1-0.3(80-1)-0.1v/Moo 0o

Military power:

8o < TRot

= 0.86o{1 - 0.16x/~o}

8o > TR

a = 0.880 { 1 - 0.16v/--~o

24(8o--TR) [

(2.55b)

(9 +

Mo)8o I

CONSTRAINT ANALYSIS 39

Turboprop

M0 < 0.I c~=80

Oo < TR

ot:80{1-0.96(M0-1) 1/4}

{ 3(O°-TR) ] (2"56)

Oo >TR

~=80 1-0.96(M0-1) 1/4- 8.13(M0-0.1)

2.3.3 Weight Fraction

In the computation of every constraint, the instantaneous weight fraction (fl) of

the aircraft is required. An initial numerical estimate for this weight fraction at

each mission junction must be based on experience. To provide you with guidance

for these estimates, the instantaneous weight fraction along the mission of two

typical aircraft, a fighter aircraft and a cargo or passenger aircraft, are shown in

Figs. 2.12 and 2.13, respectively.

2.4 Example Constraint Analysis

The performance requirements of the Air-to-Air Fighter (AAF) aircraft Request

for Proposal (RFP) in Chapter 1 that might constrain the permissible aircraft takeoff

thrust loading

(TsL/Wro)

and wing loading

(Wro/S) are

listed in Table 2.El. In

this example, we shall translate each of these performance requirements into a

constraint boundary on a diagram of takeoff thrust loading vs wing loading. This

will be accomplished with each requirement by developing an equation for the

limiting allowable loadings in the form

Z {(TsL/ Wro), (Wro/ S)} = 0

Combat

So bsonic Cruise Clim b ..............~ Escape ~=:~ ~

oovorEx .. ., S =roC

~ ~ ~ .......

~°~oen~ ~ / ~

I And #'~ ! .......... ~ ~

t Land / ~11 J ~ml ~ Combat Air Patrol

P = • R' Warm-up

and

Takeoff

Fig. 2.12 Instantaneous weight fraction: typical fighter aircraft.