Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

802 VId. Applications: Simulation of Thermofluid Systems
we find that, )(
cHp
TTcmQ −=
. Substituting for ∆T we obtain the natural cir-
culation flow rate in steady state operation as:
3/1
Core
2
H2
¸
¸
¹
·
¨
¨
©
§
=
Rc
Qg
m
p
th
NC
ρβ
VId.3.18
Equation VId.3.18 provides a reasonable estimate for the natural circulation flow
rate provided that the system resistances are closely approximated and the flow
regime is turbulent (see Problem 16).
Example VId.3.4. Find the natural circulation flow rate using the data of the
simplified PWR loop shown in Figure VId.3.4. Core power during shutdown is
5 MW. Data: f = 0.01,
ρ
= 45 lbm/ft
3
, c
p
= 1.3 Btu/lbm·F,
β
= 0.001 R
-1
, (Z
th
)
SG
= 60 ft, (Z
th
)
RPV
= 30 ft.
Solution: We must first find the loop flow resistance using the specified friction
factor of 0.01. Substituting values in
()
2
/K/
kkkkkk
ADLfR += yields:
R
1-2
= 3.86E-3 ft
-4
, R
2-3
= 8.34E-3 ft
-4
, R
3-4
= 3.12E-3 ft
-4
, and R
4-1
= 0.05 ft
-4
.
Thus, ΣR = 0.065 ft
-4
. We now substitute values into Equation VId.3.18:
3/1
2
065.03.1
)3600/3412000,5(30)-(60452.32001.02
¸
¸
¹
·
¨
¨
©
§
×
××××××
=
NC
m
= 603 lbm/s
Having determined the hydrostatic pressure head and the natural circulation
flow rate we now proceed to deal with the pump head.
4. Mathematical Model for PWR Components, Pump
In Section 3, we used the pump flow rate as a known function. In this section, we
want to find how such a function can be obtained. To find the pump speed, we
apply the conservation equation of angular momentum to the impeller of a cen-
trifugal pump. Assuming the prime mover is an electric motor, the electric torque
(T
E
) must provide for the hydraulic torque (T) and the frictional torque (T
F
). The
net torque according to Newton’s second law is then equal to the moment of iner-
tia times the rate of change of the impeller angular velocity:
dt
d
I
FE
Ȧ
TTT =−− VId.4.1

4. Mathematical Model for PWR Components, Pump 803
where I in Equation VId.4.1, represents the moment of inertia of the pump shaft,
impeller, and flywheel. The electric torque delivered by the prime mover is a
known quantity. If the pump is turned off, the electric torque drops exponentially
as:
)/2(
o
o
Ȧ
Ȧ
TT
e
t
EE
e
τ
−
=
where the rated electric torque, T
Eo
is provided by the electric motor manufacturer.
Also
τ
e
is the electric motor decay constant, which accounts for the inertia of the
electric motor. To obtain an instantaneous loss of the applied torque, the decay
constant may be set equal to a small value such as 0.1
µ
s. The hydraulic torque,
T, due to the momentum transfer from the pump impeller to the liquid is obtained
from the pump homologous curves as discussed in Chapter VIc. Finally, the fric-
tional and windage torque, T
F
accounts for all the losses in the contact points in
such places as the bearings and the pump seals. The frictional and the windage
torques may be correlated to the pump speed ratio by fitting a curve to pump
coastdown data.
4.1. Implementation of Pump Model in Momentum Equation
Determination of flow rate as a function of time due to pump startup or shutdown
in a multi-loop PWR requires simultaneous solution of the conservation equation
of momentum, for the fluid, and conservation equation of angular momentum for
the pump impeller. The momentum equation for the fluid is written as:
),Ȧ,()(
V
V
V
mmF
dt
md
A
L
dt
md
A
L
kk
L
k
k
k
=+
¦
VId.4.2
where
V
m
represents flow rate through the vessel, being the common flow path,
i.e.
¦
=
L
k
mm
V
where the summation is for the total number of loops. Func-
tion F, in Equation VId.4.2, is given by the right side of Equation VId.3.8 with
pump head given by Equation VIc.4.1. Similarly, we may express Equation
VId.4.1 as:
)Ȧ,(
Ȧ
kk
k
mG
dt
d
=
If the transient is due to pump shutdown then, without the imposed electrical
torque, the flow rate drops to the natural circulation flow rate at a rate determined
by the pump inertia, pump frictional resistance, and the hydraulic torque. This set
of equations can be generalized, using matrix notation for the multi-loop configu-
ration, as:
)(YBYA =

804 VId. Applications: Simulation of Thermofluid Systems
In this relation, matrix A is a square matrix. Elements of vector Y consist of all of
the unknowns including the unknown loop flow rate, vessel flow area, and the
pumps angular velocities:
[]
T
nn
mmmY
V11
,Ȧ,...,,Ȧ,
=
and elements of vector B are:
[]
T
nn
GFGFB ,...,,,
11
=
To solve this set by a semi-implicit finite difference scheme, we first linearize the
differential equations to set up the Jacobian matrix, which is given as
[
]
11
)(
++
∆+∆=∆
NNNNN
YJYBtYA
where superscript N represents the previ-
ous time step and J represents the Jacobian matrix. This equation can be rear-
ranged to get:
[]
NNN
N
YBtYJtA ∆=∆∆−
+1
VId.4.3
If we represent
[] [ ]
JtAC ∆−= then matrix [C] would have the following struc-
ture:
[]
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
−−−−
=
101010101
0)4()4(000000
)4()4()4(000000
000)3()3(0000
)3(00)3()3(0000
000
00)2()2(00
)2(0000)2()2(00
0000000)1()1(
)1(000000)1()1(
2221
131211
2221
131211
2221
131211
2221
131211
cc
ccc
cc
ccc
cc
ccc
cc
ccc
C
where elements of matrix C, as calculated by Kao, are given in Table VId.4.1.
Table VIc.4.1. Elements of matrix C
Element Mathematical Expression
)(
11
kc
() ( )
¦
∂∂∆−
k
N
kk
mFtAL
//
)(
12
kc
()
N
k
Ft Ȧ/ ∂∂∆−
)(
21
kc
()
N
k
Gt Ȧ/ ∂∂∆−
)(
22
kc
()
N
k
Gt Ȧ/1 ∂∂∆−
)(
13
kc
()
N
k
mFtAL )/(/
V
V
∂∂∆−
4. Mathematical Model for PWR Components, Pump 805
In this section we found numerical solution for the loop flow rate as a function
of time. Next we find analytical solutions for the loop flow rate versus time in
two cases of pump imposed transients. In the first case, we assume that the pump
head remains constant and is independent of flow rate and in the second case, we
account for pump head being a function of the loop flow rate.
4.2. Analytical Solution for Flow Transients, Constant Pump Head
Our goal is to find an analytical solution to the loop flow rate in such transients as
pump shutdown or pump start up. For now, we assume that the pump head is a
weak function of flow rate so that it can be treated as a constant in the loop mo-
mentum equation. Later in this chapter, this assumption is relaxed and the pump
head is treated as a function of flow rate. The pump head being a constant is a
reasonable assumption in certain cases. For example, at low flow rates as shown
in Figure VIc.3.1, pump head remains relatively flat and it changes rather slightly
with flow rate. Another example includes cases where the pump inertia is small as
compared with the loop fluid inertia, which makes an analytical albeit approxi-
mate solution possible.
To derive the analytical solution for flow transients we start with the single-
loop of Figure VId.3.4 and use Equation VId.2.3. Since this equation is obtained
for a single node, we integrate it over all the nodes comprising the loop. By doing
so, the static pressure differential term cancels out. The integration of Equation
VId.2.3 is equivalent to summing up all the terms of Equation IIIa.3.44 around the
loop. This results in:
()
k
n
k
n
k
n
k
kk
k
jj
k
k
jjk
n
k
pump
k
D
L
f
A
m
AA
m
ZZgP
dt
md
A
L
¦¦ ¦¸
¹
·
¨
©
§
+−
¸
¸
¹
·
¨
¨
©
§
−−−
¦
−∆=
¸
¹
·
¨
©
§
== =
+
+
= 11 1
2
2
22
1
2
1
1
K
1
2
111
2
ρ
ρ
ρ
VId.4.4
where an average density is used for each node. For example, in the core
2/)(
HLCLcore
ρρρ
+= . Since in this example, flow area remains constant
within each control volume, the summation term for the geometric inertia is sim-
plified and is made over the five primary side nodes. Equation VId.4.4 is a first
order, linear differential equation of the following form:
dt
mCC
md
=
−
22
2
2
1
VId.4.5
where coefficients
2
1
C and
2
2
C represent:
()
¦¸
¹
·
¨
©
§
»
¼
º
«
¬
ª
−
¦
+∆=
=
+
=
n
k
k
jj
n
k
kpumpc
A
L
ZZgPgC
1
1
1
2
1
ρ
¦¸
¹
·
¨
©
§
»
»
¼
º
«
«
¬
ª
¦¦¸
¹
·
¨
©
§
++
¸
¸
¹
·
¨
¨
©
§
−=
===
+
n
k
k
n
k
n
k
kk
k
jj
k
A
L
D
L
f
A
AA
C
111
222
1
2
2
K
1111
2
1
ρ
ρ

806 VId. Applications: Simulation of Thermofluid Systems
To find an analytic solution for the above first order differential equation, we write
it as
dtC
mCC
md
mCC
md
1
2121
2=
+
+
−
this can be easily integrated to obtain:
321
21
21
2ln CtCC
mCC
mCC
+=
−
+
VId.4.6
Where C
3
is the constant of integration and is determined from the initial condi-
tion. The above solution applies to both cases of pump start up in a stagnant loop
and pump shutdown in a forced flow loop. The difference is in the application of
the boundary condition to obtain the constant C
3
, as discussed next.
Case 1. Pump Start Up in a Stagnant Loop. Several conditions may lead to
stagnation in flow loops. For example, there would be no flow if the thermal cen-
ter of the heat sink is located below the thermal center of the heat source. Other
examples include a flow loop with very high frictional losses resulting in insig-
nificant rate of flow or an isothermal flow loop where
ρ
H
=
ρ
C
. In a stagnant loop,
m
(t = 0) = 0 hence, C
3
= 0. Equation VId.4.6 simplifies to:
1
1
)(
21
21
2
2
2
1
+
−
¸
¸
¹
·
¨
¨
©
§
=
tCC
tCC
e
e
C
C
tm
VId.4.7
At steady state, when t ĺ, forced circulation flow rate is found as
21
/ CCm
FC
=
.
Case 2. Pump Start Up in a Natural Circulation Loop. If a flow loop with
pump turned off operates in natural circulation mode then
m
(t = 0) =
NC
m
hence,
()()
312 12
ln[ / ]
NC NC
CCCmCCm=+ −
. Substituting for C
3
, Equation VId.4.6 be-
comes:
1
1
)(
22
21
2
2
2
1
+
−
¸
¸
¹
·
¨
¨
©
§
=
tCC
NC
tCC
NC
ey
ey
C
C
tm
VId.4.8
where in Equation VId.4.8
)/()(
2121 NCNCNC
mCCmCCy
−+= . At steady
state, when t ĺ, forced circulation flow rate is found as
21
/ CCm
FC
=
.

4. Mathematical Model for PWR Components, Pump 807
Example VId.4.1. Consider the flow loop of Figure VId.3.4 as described in Ex-
ample VId.3.4. We now start up the pump. Pressure rise over the pump is 50 psi.
Find flow rate one second after start up and at steady state.
ρ
H
= 44.5lbm/ft
3
and
ρ
C
= 45.5 lbm/ft
3
.
Solution: To calculate coefficients C
1
and C
2
of Equation VId.4.5 we find:
Σ(L/A)
k
= (174/20) + (18/37) + (75/20) + (66/19.5) = 16.3 ft
-1
Σ(
ρ
g∆Z)
k
= (
ρ
C
–
ρ
H
)gH
th
= (45.5 – 44.5) × 32.2 × (60 – 30) = 966 lbm·ft/s
2
Σ(R/
ρ
)
k
= (3.86E-3/45.5) + (8.34E-3/45) + (3.12E-3/44.5) + (0.05/45) = 1.45E-3
(ft·lbm)
-1
C
1
= [(32.2 × 50 × 144 + 966)/16.3]
1/2
= 119.5
C
2
≅ [(0.5 × 1.45E-3)/16.3]
1/2
= 6.7E-3
C
1
C
2
= 0.8 and C
1
/C
2
= 17,836 lbm/s
07.1
6033E7.65.119
6033E7.65.119
=
×−−
×−+
=
NC
y
1)6.1exp(07.1
1)6.1exp(07.1
836,17)(
+
−
=
t
t
tm
)1( =tm
= 17,836 × (1.07e
0.8
– 1)/(1.07e
0.8
+ 1) = 17,836 × 0.41 = 7,313 lbm/s
ss
m
−
= 17,836 lbm/s.
Case 3. Pump Shutdown in a Forced Circulation Loop. A similar solution can
be found for the flow coast down due to the termination of pump operation. In
this case, at time zero, the flow rate is equal to a specified steady state forced cir-
culation flow. The intention is to obtain flow rate as a function of time after the
pump is turned off. In this case, at time zero,
FC
mm
= , i.e., a known value.
Therefore, for this case the constant
3
C can be determined as
3
C =
()()
12 12
ln[ / ]
FC FC
CCm CCm+−
. Substituting, the flow coastdown is found as:
1
1
)(
22
21
2
2
2
1
+
−
¸
¸
¹
·
¨
¨
©
§
=
tCC
FC
tCC
FC
ey
ey
C
C
tm
VId.4.9
where in Equation VId.4.9,
)/()(
2121 FCFCFC
mCCmCCy
−+= .
In both cases of pump startup and shutdown, the integration of Equa-
tion VId.4.6 was easily carried out due to our simplifying assumption that the
pressure increase over the pump is independent of the flow rate. Next, we con-
sider a more general case of pump pressure rise being a function of the loop flow
rate.
808 VId. Applications: Simulation of Thermofluid Systems
4.3. Analytical Solution for Flow Transients, Pump Head a Function
of Flow Rate
The rigorous approach that resulted in obtaining Equation VId.4.3 requires nu-
merical solution. Here we seek an approximate but analytical solution to the flow
coastdown in a thermalhydraulic loop. For this purpose we consider the reactor
coolant pump in Figure VId.3.2 being turned off. We are interested in the early
part of the transient when flow is coasting down. In steady state operation, identi-
fied with subscript o, we have:
()
2
o
oo
2
1
H
2
k
kP
kk
Lm
f
ggds
DA
ρρ
ρ
´
µ
¶
¦
=+⋅
v
JJG
G
VId.4.10
where H
Po
is the pump head in steady state. Approximating the hydrostatic force
by using the thermal expansion coefficient, we get:
() ( )
³
oooo
H.
Sth
gZTgsdg
ρβρρ
=∆=
K
K
VId.4.11
where Z
th
is the difference in the elevations of the heat source and heat sink ther-
mal centers, as shown in Figure VId.2.3,
ρ
o
is density at a reference temperature
T
o
, and H
so
is the hydrostatic head at steady state. Assuming that the friction fac-
tors in the transient remain the same as in steady state and using an average flow
rate for the entire loop, the momentum equation integrated over the loop yields:
()()()
¦
+++−=
SPSP
gmm
g
dt
md
A
L
HH/HH)(
2
ooo
2
o
ρ
ρ
ρ
VId.4.12
As recommended by Burgreen, we further assume that both the pump head ratio
and the torque ratio in the transient will follow the same homologous curves as in
steady state operation. For the pump head, using the pump affinity laws, we can
then write H
P
/H
Po
= (ω/ω
o
)
2
. Also noting that for the early part of the pump shut-
down transient,
ρ
≅
ρ
o
and H
S
≅ H
So
, Equation VId.4.12 simplifies to:
()
()
¦
+++−=
o
2
oo
2
ooo
HȦ/ȦHV/V)HH(
V
)(
SPSP
ggg
dt
d
A
L
VId.4.13
For further simplification, we note that early in the flow coastdown event, the con-
tribution to flow rate due to the natural circulation is exceedingly small. But as
time goes on and the pump flywheel effect diminishes, the contribution of the hy-
drostatic force increases. Hence early in the event, we can assume that H
So
≅ 0 so
that:
()
()
2
oo
2
oo
Ȧ/ȦHV/VH
V
PPL
gg
dt
d
I
+−=
VId.4.14
where in Equation VId.4.14, I
L
represents the loop inertia, Σ(L/A). For pumps
with negligible inertia, such as the canned motor and electromagnetic pumps, the
third term in Equation VId.4.14 can be ignored compared with the other two terms
and Equation VId.4.14 simplifies to
()
0V/V)/H(/V
2
oo
=+
LP
Igdtd . The so-

4. Mathematical Model for PWR Components, Pump 809
lution to this equation can be found as
o
2
oo
H/V)V/1V/1(
PL
gIt
−= . The
time for flow to decay to half of its initial value,
2/V
2
o
is, therefore, found as:
)/(gHV)(
oo2/1 PLL
It
= .
Returning to Equation VId.4.14, if we now define
Φ =
o
V/V
,
θ
= t/(t
1/2
)
L
,
and
o
Ȧ/Ȧ=Ω then Equation VId.4.14 simplifies to:
22
/ Ω=Φ+Φ
θ
dd VId.4.15
Having obtained the simplified form of the loop momentum equation following
pump shutdown, we now turn to the impeller angular momentum given by Equa-
tion VId.4.1. Neglecting the frictional losses and noting that the electric torque
goes to zero upon pump trip, we find for hydraulic torque that;
dtdI
P
/ȦT =− VId.4.16
Pump moment of inertia, I
P
, typically consists of flywheel (≅ 75%), electric motor
(
≅ 23%), impeller (≅ 1.5%) and shaft (≅ 0.5%). Using the second approximation
for pump break horsepower torque, T/T
o
= (ω/ω
o
)
2
where T
o
is obtained from T
o
=
∆P
o
o
V
/(
η
o
ω
o
). Substituting, we find
d
ω/dt = –(1/I
P
)T
o
(ω/ω
o
)
2
VId.4.17
this upon integration from time zero to any time results in:
o
2
oo
T
11 1
ȦȦ
Ȧ
P
t
I
−=
If at (t
1/2
)
P
we have ω = ω
o
/2, then (t
1/2
)
P
= I
P
(ω
o
/T
o
). Equation VId.4.17 can then
be written as d
Ω /dt +
2
Ω /(t
1/2
)
P
= 0. Changing variable from t to
θ
, similar to
Equation VId.4.15, Equation VId.4.17 becomes:
d
Ω /d
θ
+
α
Ω
2
= 0 VId.4.18
where parameter
α
in Equation VId.4.18 is given as
α
= (t
1/2
)
L
/(t
1/2
)
P
. Equations
VId.4.15 and VId.4.18 constitute a set of coupled first-order, nonlinear differential
equations describing the effects of the pump on the loop flow rate. The solution to
Equation VId.4.18 is obtained as:
Ω = 1/(1 +
αθ
) VId.4.19
Upon substituting Equation VId.4.19 into Equation VId.4.15, we obtain the gov-
erning equation during pump coastdown as:
0)1/(1/
22
=+=Φ+Φ
αθθ
dd VId.4.20
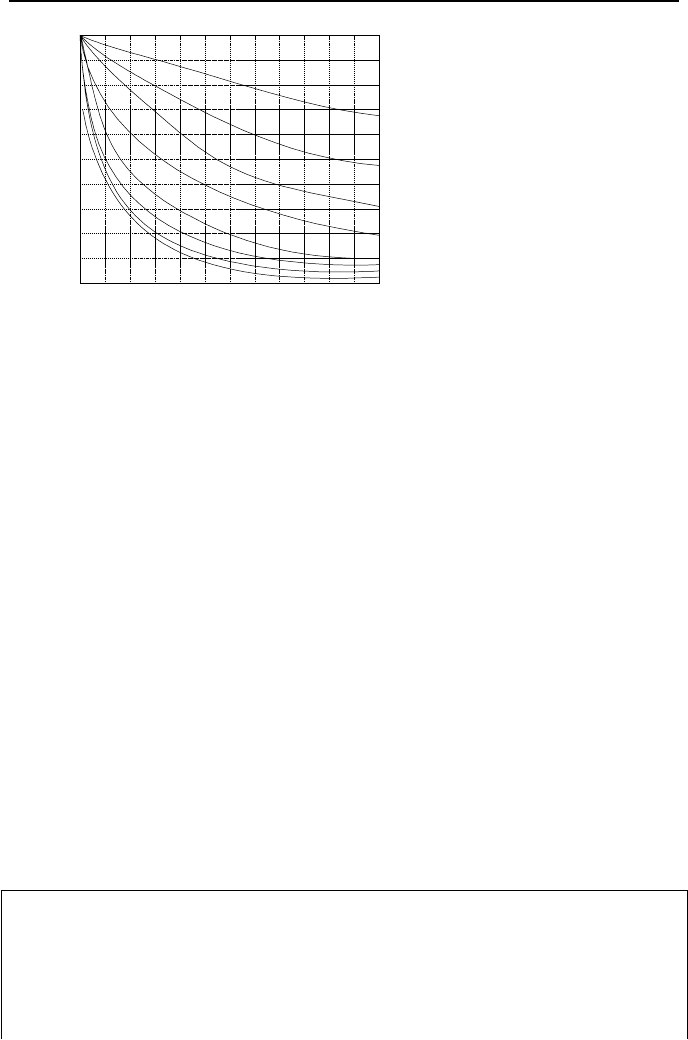
The solution to Equation VId.4.20, as offered by Burgreen, is shown graphically
in Figure VId.4.1. To get a better interpretation of
α
, we note that the initial en-
810 VId. Applications: Simulation of Thermofluid Systems
024681012
0.0
0.1
0.2
0.3
0.4
0.7
0.6
0.5
0.8
0.9
1.0
θ
, Ratio of elapsed time to loop half time
14 16 18 20 22 24
F
r
a
c
t
i
o
n
o
f
I
n
i
t
i
a
l
F
l
o
w
α
=
0
.
0
5
α
=
0
.
1
α
=
0
.
2
α
=
0
.
5
α
=
1
α
=
2
α
=
α
=
0
.
0
2
Φ,
8
Figure VId.4.1. Approximate fluid coastdown curves following pump shutdown
ergy stored in the pump is E
Po
= ½ I
P
2
o
Ȧ . Similarly, the initial stored energy in
the loop circulating fluid is E
Lo
= ½
ρ
Σ(
2
o
V
/A)LA = ½
ρ
2
o
V
I
L
. We can now ex-
press pump and fluid half-lives in terms of their corresponding initial stored ener-
gies as
(t
1/2
)
P
= 2E
Po
/(T
o
ω
o
) and (t
1/2
)
L
= 2E
Lo
/[
ρ
g
o
V
H
Po
]
Hence
α
= (t
1/2
)
P
/(t
1/2
)
L
= E
Lo
/(
η
o
E
Po
)
where we also took advantage of the definition of pump efficiency. This relation
indicates that the ratio of the fluid to pump half-lives is equal to the ratio of the
fluid to pump effective initial stored energies. Expectedly, as shown in Fig-
ure VId.5.1, if the pump flywheel contains high initial energy (
α
<< 1), reasonable
amount of fluid circulates the loop following termination of the pump operation,
due to the pump inertial effects. For small or no initial pump stored energy, as in
the case of canned motor or electromagnetic pumps, termination of the pump op-
eration results in rapid flow decay due to the action of the friction forces.
Example VId.4.2. Find the coastdown flow fraction in a flow loop at 1, 5, 7 sec-
onds into the event.
Loop Data: I
L
= ΣL/A = 108 ft
– 1
, ∆P
o
= 93 psi,
ρ
o
= 62.87 lbm/ft
3
.
Pump Data: T
o
= 636 ft lbf, I
P
= 19.5 lbm ft
2
, ω
o
= 375 rad/s,
η
o
= 0.86.
Solution: We first find volumetric flow rate at steady state:
5. Mathematical Model for PWR Components, Pressurizer 811
o
oo
o
Ȧ
V
P
T
o
∆
=
η
=
14493
37586.0636
×
××
= 15.3 ft
3
/s
To find t
1/2
, we note that H
Po
= ∆P
o
/
ρ
g
= 93 × 144/62.87 = 213 ft
213
15.3
2.32
108
H
V
)(
o
o
2/1
==
P
L
L
g
I
t
= 0.241 s
To find
α
, we need to first find (t
1/2
)
P
:
(t
1/2
)
P
= I
P
(ω
o
/T
o
) = (19.5/32.2)(375/636) = 0.357 s. Therefore,
α
= 0.241/0.357 =
0.68
We now find
θ
1
= 1/0.241 = 4.15,
θ
2
= 2/0.241 = 8.3,
and
θ
3
= 3/0.241 = 12.4.
From Figure VId.5.1, we obtain Φ
1
≅ 0.4, Φ
2
≅ 0.25, and Φ
3
≅ 0.18
Hence, V
1
≅ 0.4 × 15.3 ≅ 6 ft
3
/s, V
2
≅ 0.25 × 15.3 ≅ 4 ft
3
/s, and V
3
= 0.18 ×
15.3 ≅ 2.7 ft
3
/s.
5. Mathematical Model for PWR Components, Pressurizer
PWRs are filled with water, which remains subcooled during normal operation.
Hence, a pressurizer is necessary to control water inventory and the system pres-
sure. The volume of this tank is about 2% of the volume of the PWR primary sys-
tem. A pressurizer is usually about half filled with water and half with steam.
Since water and steam co-exist at equilibrium, both phases are saturated at the sys-
tem pressure during normal operation. The pressurizer is attached to the hot leg
through a pipe run referred to as the surge line. The vapor space allows for water
to flow from the RCS into the pressurizer (in-surge) during transients that result in
the expansion of the RCS water. The water region also allows water to flow from
the pressurizer into the RCS (out-surge) during transients that result in contraction
of the RCS inventory.
A pressurizer is equipped with spring loaded pressure safety valves (PSV), with
pilot operated relief valves (PORV), with spray nozzles, and with two sets of heat-
ers. The pressurizer design constraints include the existence of sufficient vapor
space to prevent water from reaching the relief valves and sufficient water volume
to prevent uncovering of the electric heaters. One set of heaters is designed to off-
set the heat loss through the insulation and maintain pressure. The other set of
heaters is to produce steam following an out-surge, as shown in Figure VId.5.1.
Power increase. Events resulting in a power increase cause the RCS water
temperature to rise. This is associated with an increase in water specific volume
and subsequent expansion of water. The increase in water volume results in a rush
of water from the surge line into the pressurizer and compression of steam in the
bulk vapor region. The subsequent rise in the pressurizer pressure is controlled by
