Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

782 VIc. Applications: Fundamentals of Turbomachines

a) Find the flow rate, b) How do you maximize efficiency? [Ans. a) V



= 18,655,

and b) N = 1432 rpm].

14. Solve problem 3 for

∆Z = 50 ft, D = 16 in, and L = 500 ft. All other data re-

main the same. [Ans. a)



= 28,880, b) N = 392 rpm].

15. A pump delivering water at a rate of 100,000 GPM. The maximum available

NPSH is 50 ft. Find the maximum speed to avoid cavitation.

16. In Example VIc.5.1, we derived the efficiency of a Pelton wheel in terms of

, V

, and

. Use a deflection angle of 165

, H2gV

= , and V

= ωR, as

shown in Figure VIc.5.1 and show that the Pelton wheel works most effectively

when running at half the speed of the jet of water. Find the maximum efficiency.

Comment on the actual Pelton wheel efficiency.

[Ans.:

max

= 97%.

actual

max

due to the involved frictions].

17. Find the maximum power produced by a Pelton wheel. The jet diameter is

10.45 in and the available head is 2,200 ft. [Ans.: Maximum power is the power

delivered to the jet at a C

= 1. Hence, V

= 376.4, A

= 0.596 ft



56,000 hp].

18. A screw-type reciprocating compressor having helically-grooved rotors is

shown in the figure. Mention two advantages associated with this design. [Ans.:

Pulse free and compact].

19. An impulse turbine is used to produce power from an available head of 500 m

and flow rate of 100,000 GPM. Find the diameter of the jet and the maximum

power that can conceivably be produced by the turbine.

[Ans.:

H2/V gA



and

()

max

jjj

VAW



20. An impulse turbine is operating at h = 700 m and



= 150,000 gpm. The

Pelton wheel has a diameter of 20 ft and rotating at 300 rpm. Find the power pro-

duced and the efficiency of the turbine. C

= 0.94.

[Ans.: V

= 385.6 ft/s, V

= V

/2.

21. An impulse turbine operating at a net head of 2000 ft uses a Pelton wheel of

diameter 12 ft and a jet flow area of 5 in. Find the turbine power corresponding to

the best efficiency. Use velocity coefficient of 0.94 and a bucket angle of 165

[Ans.: V

= 337 ft/s, V

= 169 ft/s, V



= 45.95 ft

/s].

Questions and Problems 783

22. Use the Bernoulli equation and show that, for a wind turbine, the wind veloc-

ity is the arithmetic average of the velocity upstream and downstream of the pro-

peller.

23. Wind is approaching a wind turbine at 27 mph, as shown in Figure VIc.5.3.

The wake wind has a velocity of 15 mph. Find a) the wind velocity at the blade

and b) the corresponding power extracted by the turbine.

24. A wind turbine has a diameter of 34 m and a power output of 350 kW at a

wind velocity of 12.5 m/s. Find the efficiency of this turbine. Assume air at 27 C.

[Ans. 33.6%].

25. A wind turbine having an efficiency of 35% and rotor diameter of 33 m is ex-

posed to air flowing at a speed of 6 m/s. Find the power developed by the turbine.

Assume

= 1.2 kg/m

. [Ans.: 38.8 kW].

26. A two-blade wind turbine is exposed to 60 mile/h wind. Downstream of the

propeller the wind speed is 45 mile/h. The propeller has a diameter of 45 ft. As-

sume ideal gas and standard condition for air to find a) the thrust on the wind tur-

bine, b) the power delivered to the wind turbine, c) the maximum power extracted

by the wind turbine, d) the maximum efficiency obtained from this wind turbine.

27. A two-blade wind turbine is installed on top of a hill experiencing winds of up

to 80 mile/h. Downstream of the propeller the wind speed is 50 mile/h. Assume

ideal gas and standard condition for air and find the tip to tip diameter of the pro-

peller to obtain a theoretical efficiency of 50%.

784 VId. Applications: Simulation of Thermofluid Systems

VId. Simulation of Thermofluid Systems

In this chapter we study the response of such systems as reactor coolant pump

(RCP), pressurizer, steam generator, containment, and the reactor coolant system

(RCS) of a PWR to imposed transients. We begin by introducing some pertinent

terms used in computer simulation and analysis of reactor thermal hydraulics.

1. Definition of Terms

Mathematical model refers to the application of the fundamental and constitu-

tive equations to represent a physical phenomenon.

Computational cell is a control volume for which the physical phenomena are

considered and mathematical models are developed. Since single-phase or two-

phase fluid may flow through a computational cell, we need to identify the number

of unknowns and set up a number of equations. For single-phase flow in a cell,

there are five unknowns namely, P, T, V

, V

, and V

. There are also five equa-

tions, conservation equation of mass, conservation equation of energy, and three

conservation equations of momentum.

For two-phase flow through the cell, there are ten unknowns namely, P, T

, T

)

, (V

)

, (V

)

, (V

)

, (V

)

, (V

)

, and void fraction (

). Similarly, there are also

ten equations consisting of two conservation equations of mass, two conservation

equation of energy, and six conservation equations of momentum. Other un-

knowns are found from constitutive equations.

Node is the same as a computational cell. For the flow of water in a pipe, for

example, we may divide the length L of the pipe into N sections. Therefore, the

pipe now consists of N nodes, each having a length of l = L/N. For single-phase

flow through the node, one pressure and one temperature would represent the en-

tire node regardless of its size. Therefore, the higher the number of the nodes, the

higher the amount of information obtained for the nodalized system. Pressure is

generally calculated at the center of the node.

Node constituents in general may include several fluid fields such as continu-

ous liquid, mixture of steam and gas, liquid droplets, and ice. The number of un-

knowns and equations increases with increasing number of the cell constituents.

For example, if a cell contains liquid, steam, ice, drops, and 10 different non-

condensable gases, there are as many as fourteen conservation equations of mass.

Nodalization. To determine the state parameters in a system, such as the pri-

mary side of a PWR, the system is broken down into several nodes. The process

is generally referred to as nodalization. Figure VId.1.1 shows a section of a sys-

tem, such as a hot leg, which is divided into N nodes with 1 ≤ k ≤ N.

Control volume for mass and energy is shown in Figure VId.1.1(a). In this

figure, nodes shown by k –1, k, and k + 1 represent three sequential control vol-

umes for calculation of mass and energy.

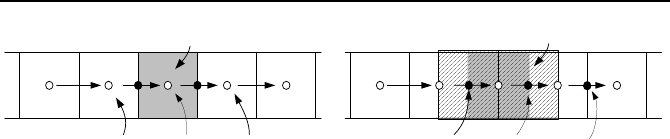
1. Definition of Terms 785

Control volume for mass and energy

k - 1 k + 1

Control volume for momentum

j - 1

j + 1

(a) (b)

Figure VId.1.1. Nodalization of a horizontal pipe

Junctions or flow paths allow separate nodes to communicate. Hence, the

mass and energy control volumes are connected together by junctions. Fig-

ure Id.1.1(b) shows junction j connecting the mass and energy control volume k to

the mass and energy control volume k + 1.

Control volume for momentum. We may assign a control volume to node j

extending from the center of node k to the center of node k + 1. This constitutes

the control volume for the conservation of momentum for this one-dimensional

flow. Momentum properties are calculated for this control volume. The most no-

table property calculated at node j is the flow velocity. Therefore, while pressure

and temperature are calculated at the center of the mass and energy control vol-

ume, flow velocity is calculated at the junction.

Donor cell can be explained by considering two computational cells exchang-

ing mass, momentum, and energy. The convective properties entering the receiv-

ing cell from the upstream cell are those of the upstream or so called donor cell.

In Figure VId.1.1 for example, the enthalpy entering node k from node k – 1 is the

enthalpy of node k – 1. Since there is no gradient inside a node, the enthalpy at

the junction between nodes k – 1 and k is the same as enthalpy at the center of

node k – 1.

Field, component, and phase. In Chapter IIIa and IIIb we dealt with homoge-

nous fields (all water, all air, etc.) In general, fields may also be heterogeneous

(Chapter IIIc). Consider for example, a vapor consisted of steam and several non-

condensable gases. Each of the constituents is referred to as a component of the

field. Phase, on the other hand, is the various forms of the same substance such as

ice, water, steam, mist, and drop.

Two-flow field model (two-fluid model) refers to the treatment of the flow

fields in a computational cell. Assuming only water and steam exist in the cell,

ten conservation equations are used in the two-fluid model to describe the condi-

tions in the cell. Thus, in this mathematical model, water and steam can be at dif-

ferent temperatures flowing at different velocities.

HEM or the homogenous equilibrium model, refers to the treatment of the fluid

in a computational cell. Assuming only water and steam exist in the cell, the two

phases are assumed to be at thermodynamic equilibrium. Thus, both phases flow

at the same velocity in the same direction having the same temperature.

SEM or the separated equilibrium model refers to a deviation from the HEM,

by the introduction of the slip ratio. This in turn requires the inclusion of the in-

786 VId. Applications: Simulation of Thermofluid Systems

Figure VId.2.1. Nodal diagram of a two-loop PWR primary side

ter-phase friction force in the momentum equation. In both HEM and SEM the

mixture properties such as

and u are obtained through the use of void fraction.

2. Mathematical Model for a PWR Loop

Determination of such parameters as pressure, temperature, and velocity in sys-

tems involving fluid flow and heat transfer is generally an involved task. A nu-

clear reactor is an example of a thermofluid system for which it is important to de-

termine such parameters by mathematical modeling. For this reason many

computer codes are developed to study various operational aspects of a nuclear

power plant. For example, several codes are devised to evaluate the thermal hy-

draulic characteristics of only the reactor core. Among the computer codes devel-

oped to analyze the reactor coolant system are RELAP, RETRAN, and TRAC. In

this section, we study the mathematical model based on the HEM for analysis of

the reactor coolant system. A nodalization example of a two-loop PWR is show in

Figure VId.2.1.

Control volumes for mass and energy (shown with subscripts k and k + 1) and

for momentum (shown with subscript j) are shown in Figure VId.2.2 for constant

and variable area channels. The conservation equations of mass, momentum, and

2. Mathematical Model for a PWR Loop 787

Momentum

Control

Volume

Mass & Energy

Control Volume

k+1

Momentum

Control

Volume

Mass & Energy

Control Volume

k+1

(a)(b)

(c)

k + 1

k+1

/ 2

k+1

/ 2

k - 1

Figure VId.2.2. Mass, ener

, and momentum control volume for channels with fixed o

variable flow area

energy are described here. The area change plays no role for the conservation of

mass and energy equations but the conservation equation of momentum, which is

more involved, must consider the variable area channel. For node k, the conserva-

tion equation of mass, Equation IIa.5.1 can be written as:

()

() ()

¦¦

−=

exitinlet

VAVA

ρρ

VId.2.1

where

= (1 –

)

αρ

and

is given by Equation Va.1.3. We may also write

Equation VId.2.1 as:



−

−1

VId.2.1-1

The conservation equation of energy as given by Equation IIa.6.4 becomes:

() ()

kjk

jjkj

Qzzg

hmzzg



−++−

−++=

−

−−

−

−−

ρρ

VId.2.2

where in Equation VId.2.2, we ignored the rate of change in the kinetic energy as

compared with the internal energy. Equation VId.2.2 includes enthalpy terms de-

veloped at the junctions. For fine nodalization, with good degree of approxima-

tion, we may use h

j – 1

= h

k – 1

and h

= h

. This is consistent with the donor cell ap-

788 VId. Applications: Simulation of Thermofluid Systems

proach. However, there are certain nodes that require special treatment such as

heated nodes within which density and enthalpy change substantially.

The one-dimensional momentum equation for the mixture can be readily ob-

tained by applying Equation IIIa.3.44 to the variable channel area of Fig-

ure VId.2.2. The momentum control volume is centered at j and it extends from

/2 and L

k + 1

/2. Substituting for various pressure drop terms, for the lower seg-

ment we get:

[( ) ( )

kkk

kk kk

dm m

LmM

Adt A

ρρ

=− − + − + +





φφ

ρρ



where

is the two-phase friction multiplier, as defined in Chapter VI. Now, we

apply Equation IIIa.3.44 to the portion of the momentum control volume extend-

ing from j, right after the change in flow area to point k + 1:

(1)/2

11 11

[( ) ( )

jjk

kk kk

dm m

Adt A

ρρ

++ ++

=− − + − + +





ρρ



Adding these equations, the result for the one dimensional momentum equation

for variable area channel becomes:

2222

11 1

(1)/2

/2 1

222

[( ) ( ) ( )

()( K]

222

pump

kk kk k k

kk k k

kk k

jjkk k k

kk k k

AAdt

PPP

AAAA

Mmmmm

ML L

gf f

AA D D

AAA

ρρ

ρρρ

++ +

ªº

«»

¬¼

∆− −+ − − −

−+ + +





  

VId.2.3

Example VId.2.1. Start with Newton’s second law and derive Equation VId.2.3.

Solution: The momentum equation expresses that the net momentum flux to or

from a control volume plus the rate of change of momentum in the control volume

is equal to the net external forces acting on the control volume. We now apply

this principle to a differential control volume located between z and z + dz. This

control volume has a flow area of A and a hydraulic diameter of D

. External

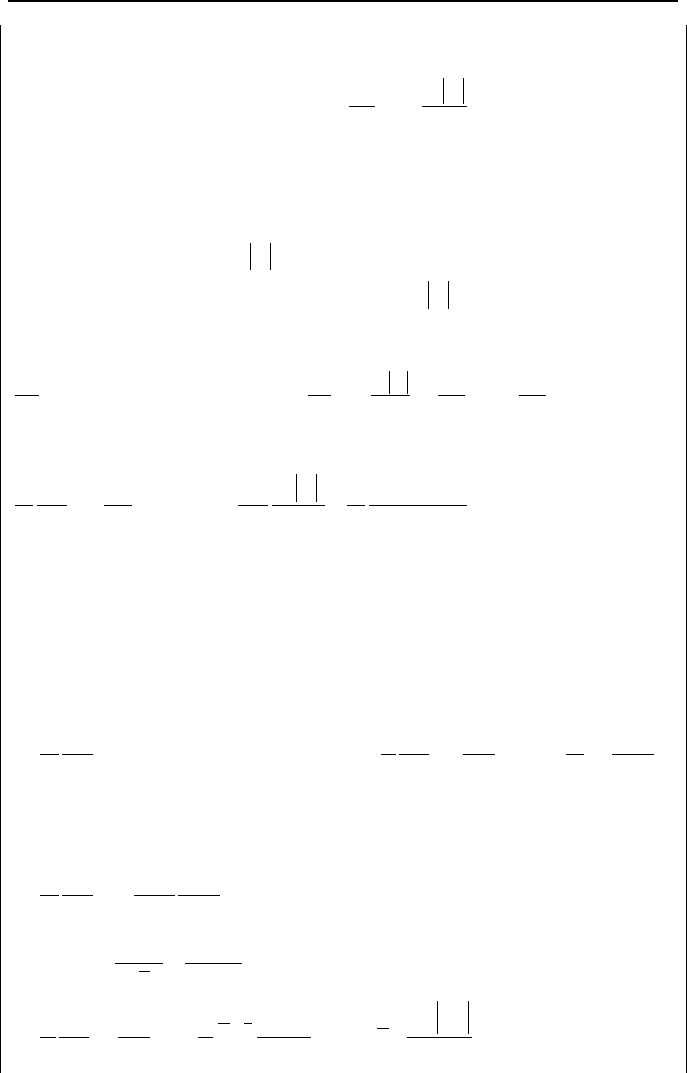
2. Mathematical Model for a PWR Loop 789

forces are the body force and the surface forces. Hence, the net force acting on the

control volume becomes:

()()(K)

zzdz

dF A P P s Adz g f

ρφ

=−− − +



where s is introduced to account for the flow direction. For upward flow s = +1,

for horizontal flow, s = 0, and for downward flow s = –1. The absolute value for

flow rate signifies the fact that the friction force acts always opposite to the flow

direction. Hence using the convention of 0>m



for up-flow, the friction force

becomes negative i.e., kFF

−= . Similarly for down-flow ( 0<m



), the friction

force would act in the direction of the z-axis, kFF

= . Accounting for the rate

of change in momentum flux, the rate of change of momentum of the control vol-

ume is therefore given by:

()()(K)[()()]

zdz zdz z

mdzmm

dz A P P s Adz g f

tDAAA

ρφ

ρρ ρ

+ +

∂

=−− − + − −

∂





We now divide both sides of this equation by Adz and let dz approach zero:

fgs

∂

−−−

∂

−=

∂

∂ )/(1

φρ







We may apply this equation to the control volume of Figure VId.2.2(c), which is

located between elevations Z

and Z

k+1

. To obtain the momentum equation for this

control volume, we multiply both sides of this equation by dz and integrate the re-

sulting equation first over the portion of the momentum control volume extending

from k to j right before the flow area changes. Integration over the lower portion

of the control volume yields:

()

−

−−−−=

gdzsPPdz

)(



Term by term integration is carried out as follows:



≈

gsMgsL

gdzs

2v2



v)K

(



790 VId. Applications: Simulation of Thermofluid Systems



−=

Adding up terms we get:

)

(

v)K

(

)(

gsL







−−

+−−−−=

We now apply the resulting equation to the portion of the momentum control vol-

ume extending from j, right after the change in flow area, to point k+1, yielding:

111

1111

11,11

() ( K)v

22v22

()

ki k k

kj k kk

kkekk

Ldm sLg L

PP f

Adt D A

+++

++++

=− − − − +

−−





Adding these equations, to get the one dimensional momentum equation for vari-

able area channels:

)]

(

)

()

(

)(

)[(

kkk

kki

kkkpump

AAA

gLLs

PPP











+++

−−−

+−−∆=

This equation includes a pressure rise term in case there is a pump in the flow

path. This equation while derived for single-phase flow is applied to two-phase

mixture with the introduction of the multiplier

and v .

Equations VId.2.1, VId.2.2, and VId.2.3 constitute a set of differential equa-

tions in mass, internal energy, and mass flow rate. Writing similar sets for the rest

of the nodes would result in a system of differential equations, which upon solu-

tion would result in obtaining the key parameters versus time. The initial condi-

tions are found from the steady state operation prior to the imposition of a tran-

sient.

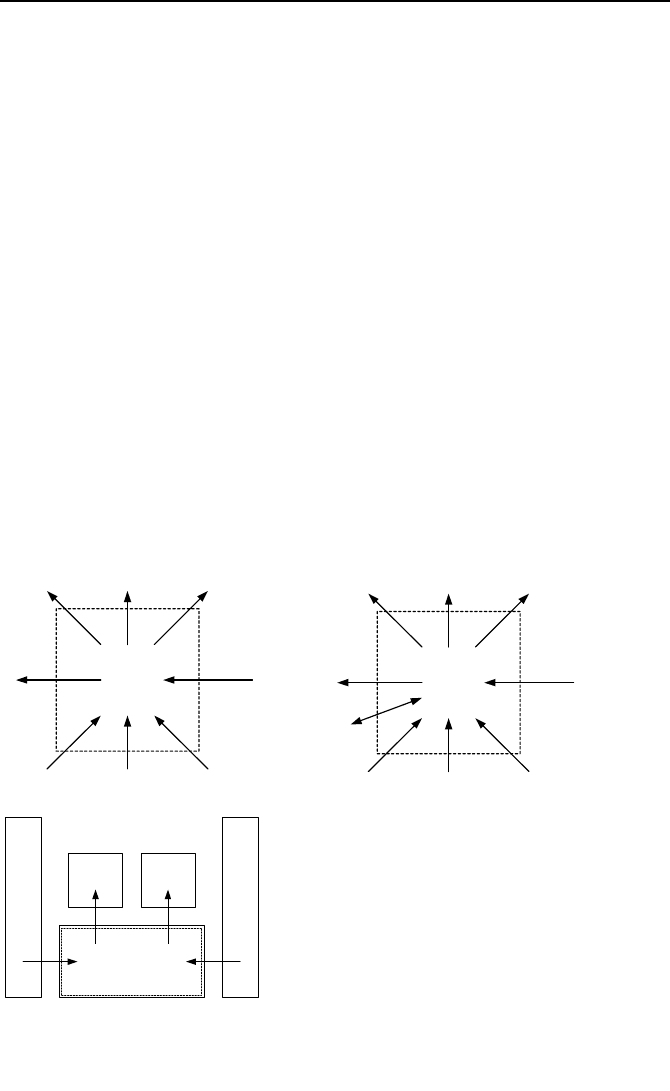
3. Simplified PWR Model 791



()



()



()



(a) (b)

Downcomer

core core

Lower plenum

(c)

Figure VId.3.1. (a) mass and (b) energy transfer for a typical node. (c) Exam

le of

multi-port node

3. Simplified PWR Model

The level of information obtained from a mathematical model depends on the ex-

tent of complexities used in the model such as the multi-dimensional analysis of

multi-component flow. We may introduce a variety of simplifying assumptions to

reduce the computational burden and obtain results with reasonable accuracy.

However, simplifying assumptions impose limitations on the applicability of the

model. An example of a simplifying assumption is the application of an integral

or loop-wide momentum equation. This assumption decouples the solution of the

momentum equation from the mass and energy equations. To see the saving in the

number of equations, consider a case where there are N nodes in each loop of Fig-

ure VId.2.1. According to the model developed in Section 2, there are a total of

6N equations for the N nodes. By writing an integral momentum equation for

each loop, the number of equations drops to 2N + N’ where N’ is the number of

loops. An integral momentum equation ignores the compressibility of fluid due to

the local pressure changes and assumes that the pressure and velocity disturbances

are propagated at infinite velocity. This allows us to assign one pressure to the en-

tire RCS and one loop flow rate to each loop.

Let’s now obtain the set of equations for node k (Figure VId.3.1) using the

above simplifying assumption. For this purpose, we consider the various interac-

tions with node k. Flow may enter this node from several inlet ports (shown with

subscript i) and leaves from several exit ports (shown with subscript e). These are